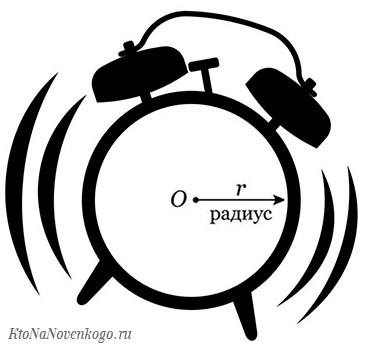
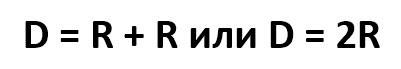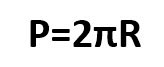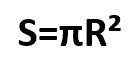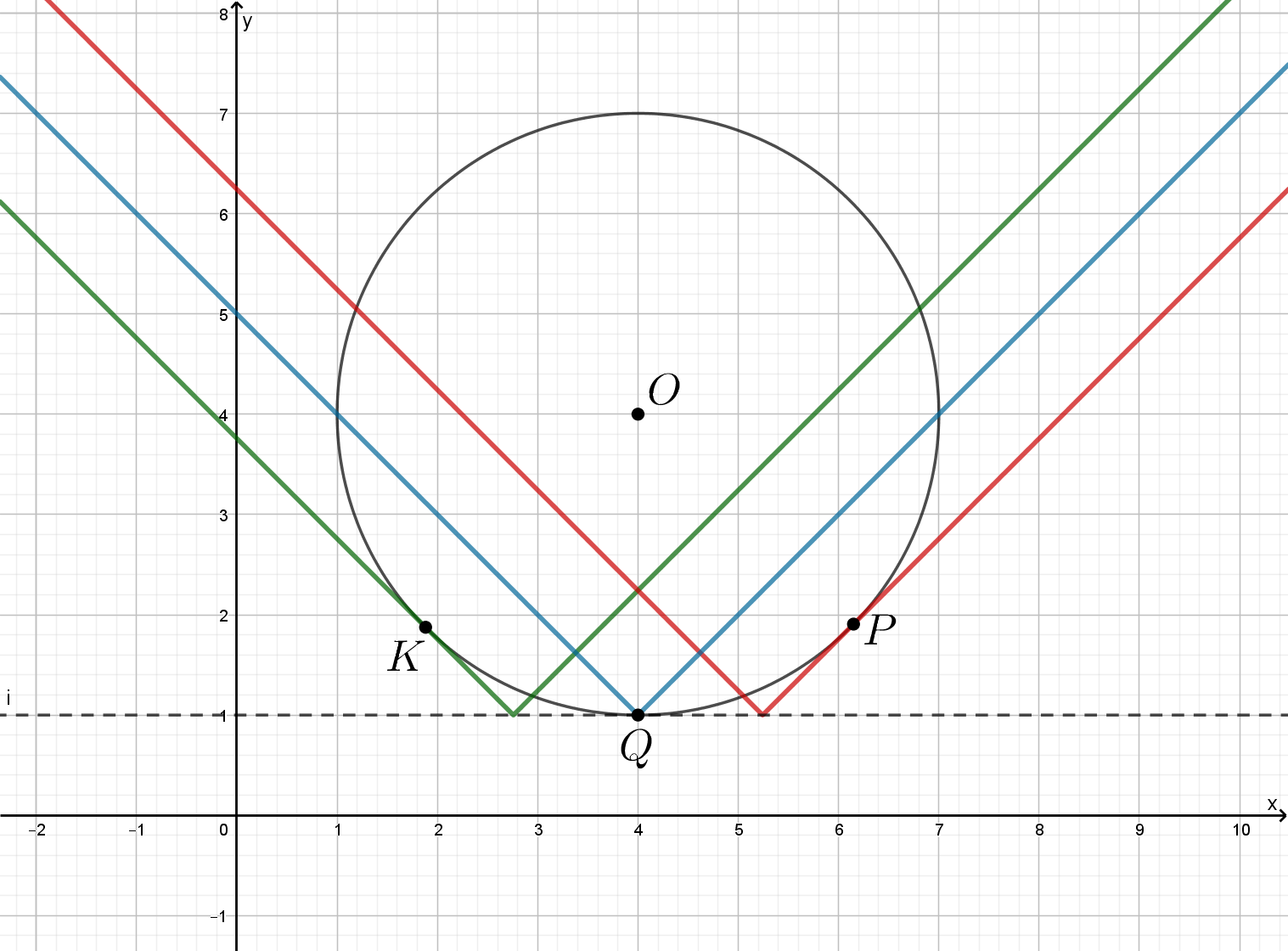Как найти радиус окружности параметр - Сайт, где вы сможете решить свои вопросы

Радиус — это важнейший элемент окружности

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы продолжим знакомить вас с различными математическими терминами. И расскажем, что такое РАДИУС.

На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.

Что такое радиус

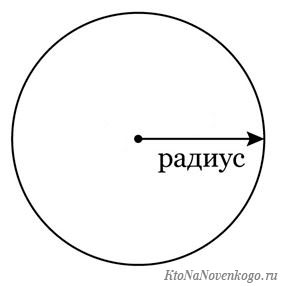
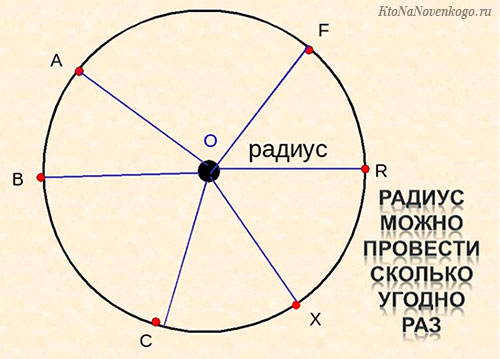
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.

Вот так это выглядит графически.

Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.

Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.

Кстати, есть еще несколько значений слова РАДИУС:

Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
В анатомии этим словом обозначают Лучевую кость предплечья.

Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

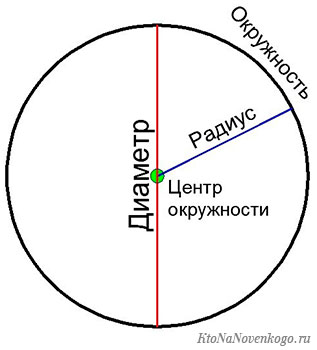
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

Длина диаметра равна удвоенной длине радиуса.

Свойства радиуса

В отношении радиуса действуют несколько важных правил:

Радиус составляет половину диаметра. Это мы продемонстрировали только что.
У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

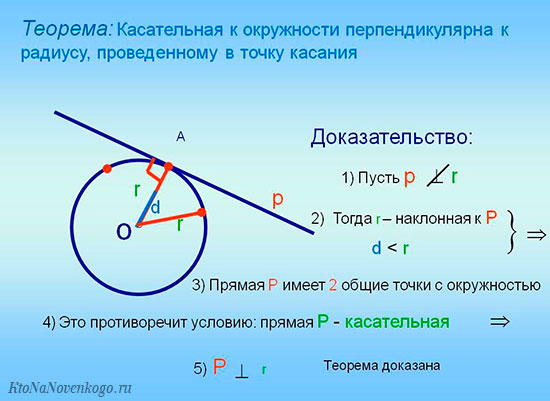
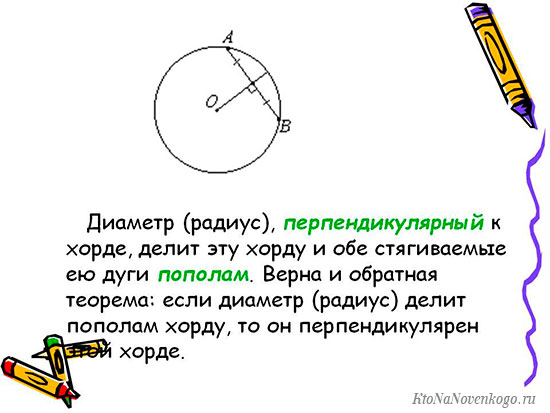
Радиус, который перпендикулярен хорде, делит ее на две равные части.

Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

Длина и площадь окружности через радиус

Об этих математических величинах мы решили рассказать не случайно. Дело в том, что при их вычислении просто необходимо знать значение радиуса. И наоборот, зная длину окружности или ее площадь, можно найти радиус.

Длина окружности

Длина окружности – это кривая, которая состоит из точек, равноудаленных от центра окружности. Проще говоря, это длина поверхности окружности.

Длина окружности одновременно является и ее периметром, а потому в геометрии она обозначается латинской буквой «Р» (иногда встречаются и «L», и «C»). А формула для ее вычисления выглядит следующим образом:

Иногда ее пишут и как P=πD, так как 2R – это удвоенный радиус, что, как мы уже сказали выше, является диаметром. Но классическая формула во всех учебниках дается все-таки через радиус.

Гораздо интереснее здесь рассмотреть величину, обозначаемую буквой π. Это как многим известно, математическая постоянная. Она произносится как «Пи» и равна 3,14.

Хотя на самом деле количество знаков после запятой у «пи» не ограничено. Но для простоты вычислений решено брать именно так.

Площадь окружности

Площадь окружности – это пространство, которое находится внутри ее периметра. Она обозначается латинской буквой «S». А формула для ее вычисления выглядит так:

Опять же, здесь R- это радиус, а π – математическая постоянная, равная 3,14.

Вместо заключения

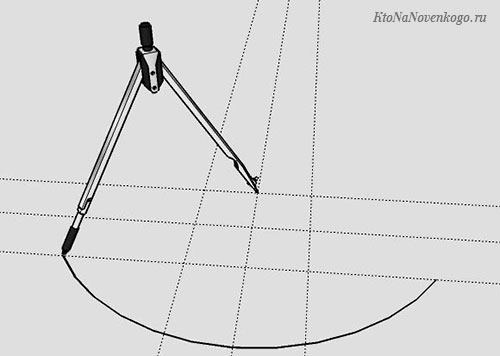
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.

Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Геометрия была моим любимым предметом в школе. Особенно любил тригонометрию, но и с окружностями был на короткой ноге. Радиусы, диаметры и длину окружности могу определить до сих пор.

Меня восхищают люди, которые знают число Пи на память) Это же надо так математику любить)

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Нахождение радиуса круга: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:

C = 2 π R

π – число, приближенное значение которого равно 3,14.

2. Через площадь круга

Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:

S = π R 2

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/radius-okruzhnosti

Нахождение радиуса круга: формула и примеры

[/spoiler]

Источник

Тема 17.

Задачи с параметром

Графика. Окружность

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами – ЛЕГКО!

Подтемы раздела

задачи с параметром

Решаем задачи

Найдите все значения параметра , при каждом из которых система

({ 2 2 2
x +y − 2a(x+ 2y)= 5− 5a
(y + 1x= 0
2

имеет решения.

Показать ответ и решение

Преобразуем первое уравнение:

2 2 2
x + y − 2a(x+ 2y)= 5− 5a ⇔

2 2 2 2
⇔ x + y − 2ax − 4ay +a +4a = 5 ⇔

2 2
⇔ (x− a) +(y− 2a) = 5

Оно задает окружность с центром в точке O(a;2a) и радиусом √-
5. Найдем траекторию центра окружности:

({
x =a ⇒ y = 2x
( y = 2a

Таким образом, первое уравнение исходной системы задает окружность с центром в произвольной точке прямой y = 2x и
радиусом √ -
5. Второе уравнение исходной системы — это прямая 1
y = −2x. Построим графики.

Нас интересуют значения при которых окружность имеет точки пересечения с прямой 1
y =− 2x, значит, ключевыми
положениями на рисунке для нас будут касания окружности с этой прямой. Заметим, что прямая y = − 1x
2 и
прямая-траектория y = 2x перпендикулярны. Следовательно, окружность будет касаться прямой 1
y = −2x только в том
случае, если ее центр находится на расстоянии, равном радиусу окружности, от точки пересечения прямых — начала координат.
Изобразим случаи касания на картинке, начало координат обозначим через центры окружностей в случаях касания — через
и O2.

Мы поняли, что точки и таковы, что Очевидно также, что a1 > 0 и
Найдем a1, записав условие на расстояние между и O1 :

√- ∘ ------2---------2 ∘ --2
5 =ρ(O1;A)= (a1− 0)+ (2a1− 0) = 5a1 ⇔ a1 = ±1

Так как a1 > 0, то получаем Очевидно, что при любых то есть когда центр принадлежит
отрезку O1O2, окружность будет иметь пересечения с прямой 1
y = −2x, а при любых для которых |a|> 1 — не будет.
Получаем ответ

Ответ:

При каких значениях параметра касаются графики, задаваемые уравнениями

2 2
x + (y− a) = 4 и y = x?

Показать ответ и решение

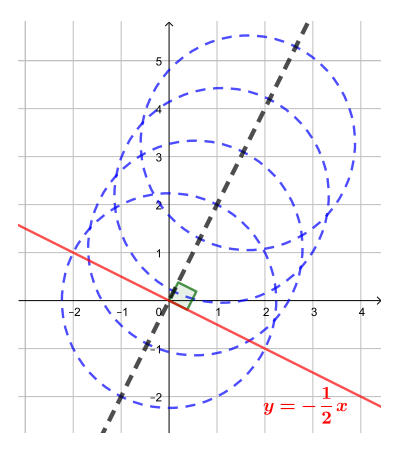
Первому уравнению соответствует семейство окружностей с центрами на оси ординат, так как координаты центра (0;a), и
радиусом, равным 2. Второе уравнение задает прямую. Построим графики.

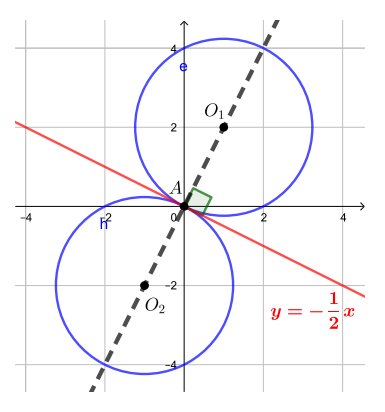
Сначала рассмотрим случай, когда a> 0, то есть центр окружности лежит в верхней полуплоскости. Чтобы окружность с
центром O (0;a) и радиусом 2 касалась прямой, расстояние от центра до этой прямой должны быть равно 2. Выразим
через расстояние от центра окружности до прямой, а затем приравняем его к 2, чтобы найти подходящие

Опустим перпендикуляр на прямую y = x, начало координат обозначим через Мы знаем, что прямая y = x
образует угол ∘
45 с осью абсцисс, следовательно, угол HAO также равен ∘
45 . Тогда треугольник OHA — прямоугольный
равнобедренный с гипотенузой OA = a, значит, его катет равен a
OH = √2-. Приравняем эту величину к радиусу и найдем
a :

-
√a-= 2 ⇔ a = 2√2
2

Для отрицательного то есть когда центр окружности лежит в нижней полуплоскости, картинка будет симметричной, а
значит, √ -
a= −2 2 нам тоже подойдет. Тогда окончательно имеем:

√- √-
a∈ {−2 2;2 2}

Ответ:

√ - √ -
{− 2 2;2 2}

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточное обоснование построения	3

Верно рассмотрено одно из двух взаимных расположений графиков функций, при этом верно найдено хотя бы одно из значений параметра	2
ИЛИ
значения параметра найдены верно, но нет обоснования их нахождения на основе взаимного расположения графиков функций

Верно сведено к исследованию графически или аналитически, при этом построение обосновано	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Найдите все значения параметра при каждом из которых система

({ 2 2
x − 8x+ y + 4y+ 15= 4|2x − y − 10|
( x+ 2y = a

имеет более двух решений.

Показать ответ и решение

Первое уравнение равносильно:

⌊({ ⌊({
| y ≤ 2x− 10 | y ≤ 2x− 10
||( x2− 8x + y2+ 4y +15 = 4(2x− y − 10) ||( (x − 8)2+ (y+ 4)2 =25
|||({ ⇔ |||({
⌈ y > 2x− 10 ⌈ y > 2x− 10
( x2− 8x + y2+ 4y +15 = −4(2x − y− 10) ( x2+ y2 = 25

Первая система задает в области под прямой часть окружности с центром в и радиусом R = 5 .
Вторая система задает в области над прямой часть окружности с центром в и тем же радлиусом. Заметим,
что эти окружности пересекаются, и пересекаются на прямой . Назовем множество, являющееся объединением этих
двух частей окружностей .

Тогда требуется найти такие положения прямой 1
y = − 2(x − a) , при которых она с множеством имеет более двух точек
пересечения.

Заметим, что угловые коэффициенты прямых и в произведении дают − 1 , следовательно, эти
прямые взаимно перпендикулярны, таким образом, прямая является осью симметрии для и для прямой :
1
y = −2(x− a) , следовательно, если касается одной окружности из , то она касается и второй окружности из
.

Найдем граничные положения этой прямой:

Следовательно, находясь в розовой области, прямая имеет с более двух общих точек.

:

касается окружностей в точках и . Найдем , задавая это положение следующим образом: расстояние
от центра второй окружности до прямой равно радиусу окружности

|x-+-2y-−-a| |a| √-
R = O2D = √1-+-22 |x=0, y=0 ⇔ 5= √5- ⇔ a =±5 5

Нам подходит меньшее (когда прямая касается окружности снизу), то есть .

:

аналогично предыдущему пункту

|x + 2y − a| |a| √-
R = O2F = -√-----2--|x=0, y=0 ⇔ 5= √-- ⇔ a= ±5 5
1+ 2 5

Нам подходит большее (когда прямая касается окружности сверху), то есть √ -
a= 5 5 .

:

B ∈l . Найдем координаты точек и как точек пересечения и окружности 2 2
x + y = 25 :

(
{ y = 2x− 10
( x2+ y2 = 25 ⇒ A(5;0), B (3;−4)

Следовательно, из B ∈ l следует

:

аналогично предыдущему пункту A ∈ l :

Следовательно, √ -
− 5 5< a≤ −5; √-
5≤ a< 5 5.

Ответ:

( √ - ] [ √-)
a ∈ − 5 5;−5 ∪ 5;5 5

Найдите все значения параметра , при каждом из которых система

({ √---------2
y = 5−√8x−-4x-+-2-------
(y +2a = 9− 4a2+ 8ax− 4x2

имеет единственное решение.

Показать ответ и решение

Перепишем систему в виде

( 2 2
||||| (y − 2) + (t+2) = 9
( √---------- |||| y− 2≥ 0
{ y− 2= 5 − 8x − 4x2 ⇔ { 2 2
( y+ 2a= √9-− 4a2+-8ax−-4x2 ||| (y +2a) + (t− 2a) = 9
||||| y+ 2a≥ 0
|( t= 2x

Так как замена t= t(x) линейная, то в новых координатах и система также должна иметь единственное
решение.

В системе координат tOy первое и третье равенства, учитывая второе и третье неравенства, задают верхние полуокружности
с центрами в точках и соответственно и одинаковыми радиусами R = 3 . Следовательно, нам
необходимо, чтобы эти полуокружности имели одну точку пересечения.

Заметим, что первая полуокружность фиксирована, а вторая при изменении от − ∞ до + ∞ движется
сверху вниз по прямой . Также заметим, что центр первой окружности тоже лежит на прямой .
Следовательно, положения второй полуокружности, при которых она имеет одну точку пересечения с первой,
такие:

Заметим, что когда правый конец одной из полуокружностей лежит на другой полуокружности, то для другой
полуокружности эта точка — наивысшая (то есть точка с максимальной ординатой) точка этой полуокружности. Речь
идет о точках и .

Действительно, AO1CO2 — ромб, так как , диагональ O1O2 которого со стороной
CO1 образует угол в 45∘ , следовательно, это квадрат, следовательно, . Аналогично для точки
.

Тогда нам подходят все положения второй полуокружности между теми, когда она проходит через точки
и (включая эти положения), исключая положение, когда она совпадает с первой полуокружностью. Так
как мы доказали, что AO1CO2 — квадрат, то ордината для “положения ” равна , а для “положения
” равна − 1 (на единицы больше/меньше ординаты ). Следовательно, , откуда

Ответ:

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

С помощью верного рассуждения получены все значения но некоторые граничные точки включены/исключены неверно	3

С помощью верного рассуждения получены не все значения	2

Задача верно сведена к исследованию взаимного расположения графика функции и прямой (аналитически или графически)	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

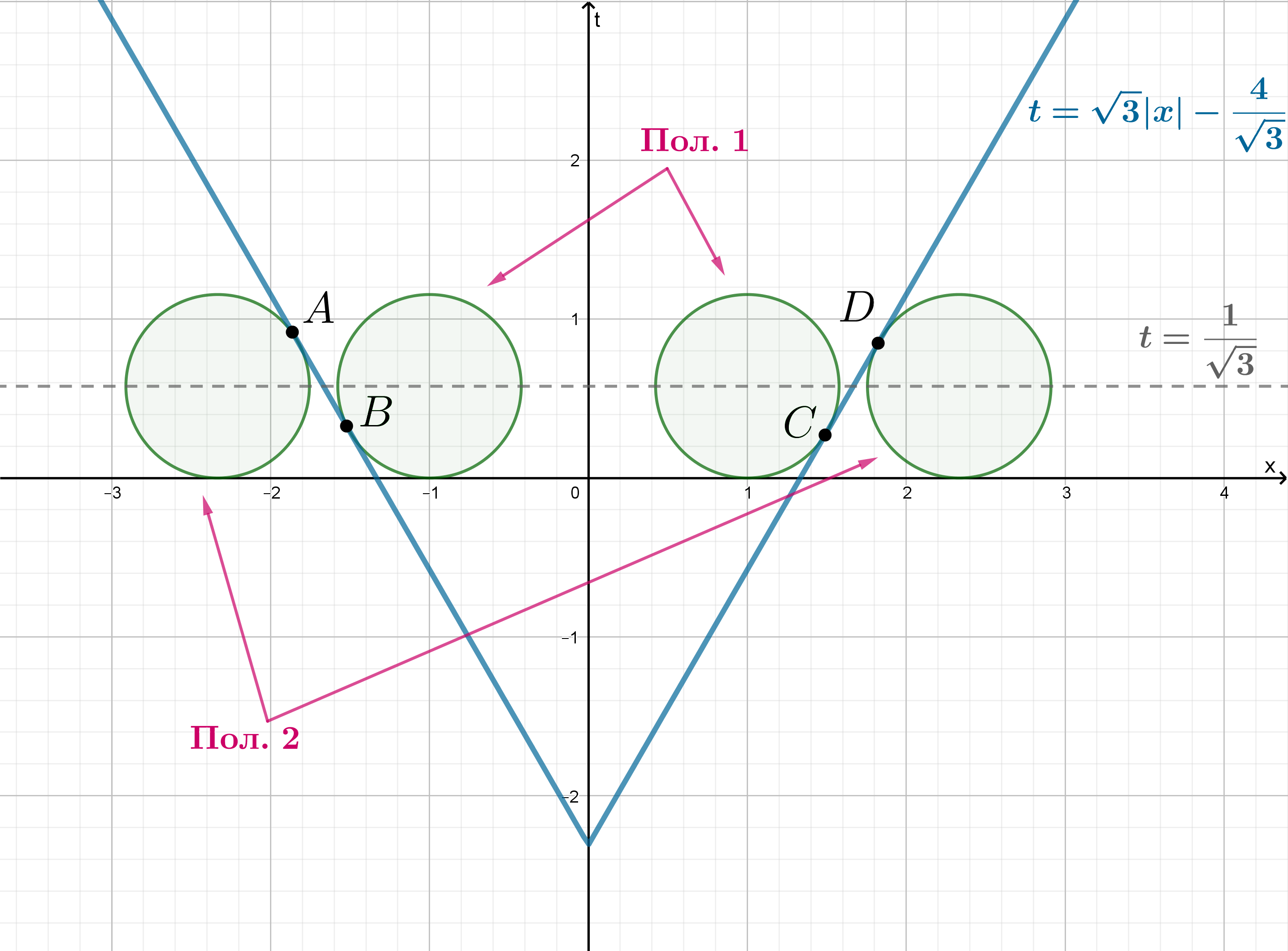
Найдите все значения , при каждом из которых система уравнений

(| 2 2 ∘------2 2 ∘------2
{ y − (x + 2|x|− x − 4)y+ (x − 4) 2|x|− x = 0
|( a+ 2x= y

имеет нечетное число различных решений.

Показать ответ и решение

По теореме Виета, если рассматривать первое уравнение как квадратное относительно , получаем

(|⌊ 2
|||||⌈y =x∘ −-4----
{ y = 2|x|− x2
||||2|x|− x2 ≥0
||(y = 2x+ a

Равенство задает верхнюю полуокружность от окружности (которая, заметим, целиком лежит в правой
полуплоскости), тогда равенство задает две верхние полуокружности и . Таким образом,
система равносильна:

(||⌊y =x2− 4
||||||| √ ----2-
||{|⌈y =√ 2x-− x--
|| y = −2x− x2
|||||−2≤ x≤ 2
||(y = 2x+ a

Изобразим график совокупности в области, задающейся неравенством и определим те положения прямой , при
которых она с этим графиком (голубой) имеет нечетное число точек пересечения.

:: прямая касается параболы в точке ;
:: прямая проходит через “стык” двух полуокружностей — через начало координат (также пересекает правую
полуокружность в точке и параболу в точке );
:: прямая касается правой полуокружности в точке (также пересекает левую полуокружность в точке и параболу в
точке );
:: прямая касается левой полуокружности в точке

Найдем значения параметра, соответствующие этим положениям прямой.

:

Ищем касание прямой и параболы (через равенство функций и производных в точке касания):

( (
{ 2x +a =x2− 4 { a= −5
( ⇔ (
2= 2x x= 1

:

прямая проходит через B2(0;0) , если

:

прямая касается окружности, если расстояние от центра окружности до прямой равно радиусу окружности:

Нашему положению соответствует большее (так как меньшее соответствует более низкому положению прямой, когда она
касается отсутствующей нижней правой полуокружности). Следовательно, √-
a= 5 − 2.

:

аналогично предыдущему пункту

|y − 2x− a| |0+ 2− a| √- √-
R = -√1-+22--|y=0; x=−1 ⇔ 1 = --√5---- ⇔ |a − 2|= 5 ⇔ a = ± 5+ 2

Нашему положению соответствует большее (так как меньшее соответствует более низкому положению прямой, когда она
касается отсутствующей нижней левой полуокружности). Следовательно,

Ответ:

Найдите все значения параметра , при каждом из которых система

({ 2 2
(x − a) + 3y − 2y = 0
( |x|− y = 43

имеет одно решение.

Показать ответ и решение

Система равносильна

( (| 2 ( 1-)2 1
|{ (x − a)2+ (√3y − 1√-)2 = 1 |||{(x− a) + t− √3 = 3
| 4 3 3 ⇔ |t= √3|x|− √4-
( y = |x|− 3 |||( √- 3
t= 3y

Так как замена t=t(y) линейная, то в новых переменных и система также должна иметь единственное решение.

Таким образом, в системе координат tOx первое уравнение задает окружность с центром в точке ( -1)
O a;√3 и радиусом -1
R= √3- ,
движущуюся по прямой 1-
t= √3 , а второе уравнение задает уголок, строящийся в следующей последовательности:
4
сжатиев√3раз √- сдвигна √3 единицвниз √ √4
|x|−−−−−−−−−−−−→ 3|x|−−−−−−−−−−−−−−−−−−→ 3|x|− 3

Одно решение система имеет в том случае, когда окружность касается уголка.

Так как график √- -4-
t= 3|x|− √3 симметричен относительно оси ординат, то в Положении 1 будем рассмативать касание окружности и
уголка в точке и в точке (причем этим касаниям соответствуют противоположные значения параметра), а в Положении 2 — касание
в точке и в точке (чему также соответствуют противоположные значения параметра).

Рассмотрим касание в точке и в точке . Тогда расстояние от центра окружности до левой ветви уголка tleft = −√3x− √4
3 равно
радиусу окружности, следовательно:

Тогда касанию в точке соответствует a= 1 , а касанию в точке соответствует 7
a= 3. Следовательно, 7
a= ±1;±3.

Ответ:

a ∈{±1;±7}
3

Найдите все , при которых система

({
y = ||x+ 3|− 1|
(x2+ y2 = 2ay− a2− 4x − 72

имеет ровно два различных решения.

Показать ответ и решение

Второе уравнение системы равносильно

2 2 1
(x+ 2) + (y − a) = 2

Следовательно, оно задает окружность с центром и радиусом √2
R= -2 . Значит, при изменении от − ∞ до
окружность движется снизу вверх по прямой x= −2 . Первое уравнение задает “птичку”, которая строится в следующей
последовательности:

Рассмотрим следующие положения:

1.

Верхняя часть окружности проходит через точку

Пусть этому положению соответствует

2.

Нижняя часть окружности проходит через точку

Пусть этому положению соответствует

3.

Окружность вписана в угол ∠MNL

Заметим, что диагональ клетки равна , следовательно, половина диагонали клетки равна . Также заметим, что две
диагонали клетки взаимно перпендикулярны, следовательно, если окружность касается , то она также касается и отрезка
, причем в серединах обоих отрезков — в точках и соответственно (так как слетка представляет собой квадрат).

Пусть этому положению соответствует .

Заметим, что при изменении от − ∞ до окружность последовательно проходит через положения 1, 2 и 3 (в указанном
порядке). Тогда нам подходят Найдем нужные значения параметра.

:

лежит на окружности:

Этому положению соответствует 1
a =− √2 , так как ордината центра окружности отрицательная.

:

лежит на окружности:

2 2 1 1
(−2+ 2)+ (0− a) = 2 ⇔ a= ±√2-

Этому положению соответствует a = 1√-
2 , так как ордината центра окружности положительная.

:

центр окружности находится в узле клетки (вершина квадрата), следовательно, a= 1 .

Таким образом, a∈ (−√1;√1) ∪{1}.
2 2

Ответ:

a ∈(− 1√-; 1√-)∪{1}
2 2

Найдите все значения параметра , при каждом из которых система уравнений

({ 2 2 2
(x− a − 1) + (y− a− 3) =(2a− 3)
((x− 2a +3)2+(y− 2a− 1)2 = (a − 2)2

имеет единственное решение.

Показать ответ и решение

Ответ:

{ 9±√46- √-}
a ∈ --7---;5± 6

Найдите все значения параметра , при каждом из которых система

({ 2 2
(x+ 2a− 1) + (y +5a− 2) =4
((x− 3a+ 1)2+ (y − 6a+ 5)2 =9

имеет единственное решение.

Показать ответ и решение

Первое уравнение системы задает окружность C
1 с центром в точке O (1 − 2a;2− 5a)
1 и радиусом R =2
1 , а второе уравнение задает
окружность с центром в точке и радиусом R2 = 3 .

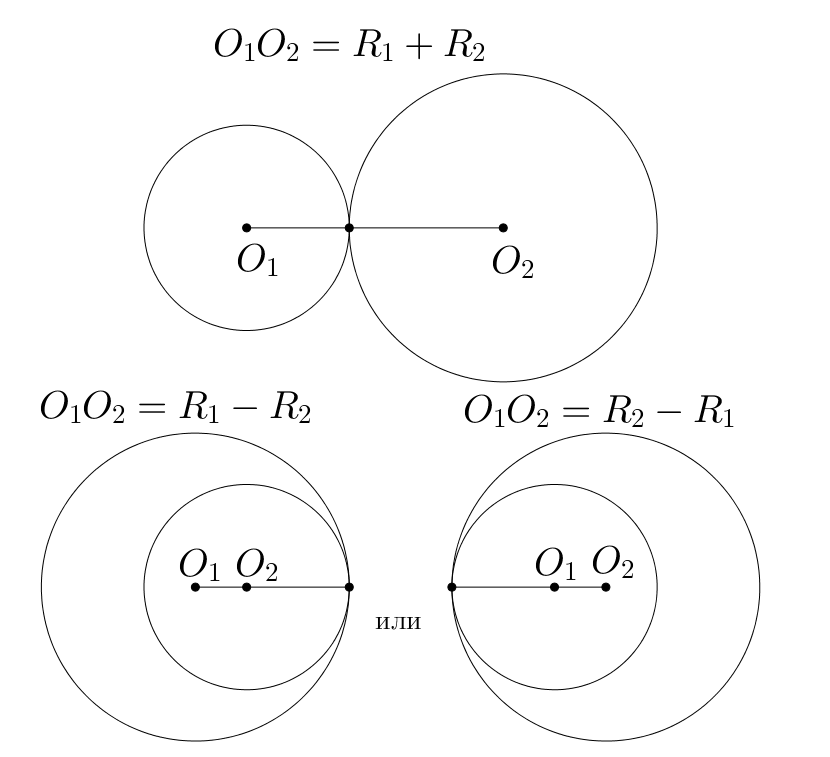
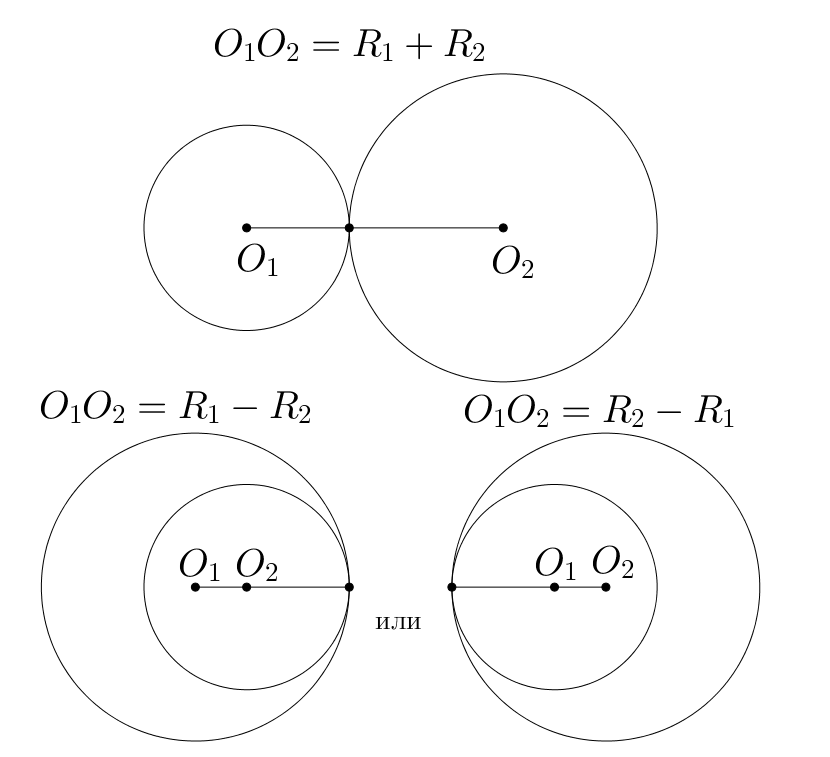
Две окружности имеют одну точку пересечения, если они касаются. При касании внешним образом сумма радиусов равна расстоянию
между центрами окружностей: ; при касании внутренним образом модуль разности радиусов равен расстоянию между
центрами окружностей: .

Следовательно,

⌊
⌊ 5= ∘(1−-2a-− 3a+-1)2-+(2−-5a-− 6a+-5)2 ⌊25 =146a2− 174a+ 53 a= 14-
⌈ ∘------------2--------------2 ⇔ ⌈ 2 ⇔ |⌈ 73
1= (1− 2a − 3a+ 1) +(2− 5a − 6a+ 5) 1 =146a − 174a+ 53 a= 1

Таким образом, 14
a= 73;1.

Ответ:

a ∈{14;1}
73

Найдите все значения параметра , при каждом из которых система уравнений

({ 2 2
x +y = 8x− 37+10y
( (x − 7)2+(y− 9)2 =a2

имеет единственное решение.

Показать ответ и решение

Преобразуем первое равенство:

2 2
(x− 4)+ (y− 5) = 4

Тогда первое уравнение системы задает окружность с центром в точке O1(4;5) и радиусом R1 = 2 , а второе уравнение задает
окружность с центром в точке O2(7;9) и радиусом при a⁄= 0 и точку при a= 0 .

В случае a= 0 система имеет единственное решение, если O ∈C
2 1 , что проверяется подстановкой координат точки в уравнение
окружности:

2 2
(7− 4)+ (9− 5) = 4

Получили неверное равенство, следовательно, , значит, a =0 нам не подходит.

Пусть . Тогда две окружности имеют одну точку пересечения, если они касаются. При касании внешним образом сумма радиусов
равна расстоянию между центрами окружностей: ; при касании внутренним образом модуль разности радиусов равен
расстоянию между центрами окружностей: |R − R |= O O
1 2 1 2 .

Следовательно,

⌊ ∘-------------- ⌊ ⌊
⌈2+ |a|= (7− 4)2+ (9 − 5)2 ⌈ 2+ |a|=5 ⌈|a|=3
|2− |a||=∘ (7−-4)2+-(9-− 5)2 ⇔ |2− |a||=5 ⇔ |a|=7

Таким образом,

Ответ:

Найдите все значения параметра , при каждом из которых система уравнений

({ 2 2
(x− 4) + (y − 4) = 9
(y = |x− a|+ 1

имеет три различных решения.

Показать ответ и решение

Первое уравнение задает окружность с центром O(4;4) и радиусом R =3. Второе уравнение задает уголок, вершина которого движется
по прямой y =1 (заметим, что эта прямая касается окружности). Причем при изменении от − ∞ до + ∞ уголок движется слева
направо. Три точки будет в следующих позициях:

касание в левой ветви уголка и окружности;
вершина уголка находится в точке касания окружности и ;
касание в правой ветви уголка и окружности.

Если прямая касается окружности, то это условие можно задать с помощью формулы расстояния от точки до прямой: в случае
окружности это расстояние должно быть равно радиусу окружности. Для центра окружности (x0;y0) радиусом и прямой ,
задаваемой , это уравнение выглядит так:

ρ(O,l)= |ax0√+-by0-+c|= R
a2+ b2

Следовательно, так как y =− x+ a+1
left , то есть y +x − a− 1= 0
left , y =x − a+ 1
right , то есть y − x+ a− 1= 0
right ,
получаем

|4+-4− a-− 1| √-
K : 3= √2- ⇔ a =7 ±3 2

P : 3= |4− 4√+a−-1| ⇔ a =±3√2-+1
2

Для точки нужно выбрать меньшее значение параметра (так как существует еще одно положение, когда левая ветвь касается
окружности, и оно правее нужного нам положения), для точки — большее значение параметра (по аналогичным причинам). Вершина
уголка в точке Q(4;1) , если a= 4 .

Следовательно, .

Ответ:

Найдите все значения параметра , при каждом из которых система уравнений

({ 2 2
(|x|− 6) + (y − 12) = 4
((x+ 1)2+ y2 = a2

имеет единственное решение.

Показать ответ и решение

Первое уравнение представляет собой две части окружностей: одна с центром в точке O (6;12)
1 и радиусом R = 2
1 , вторая — с центром
и тем же радиусом. Заметим, что расстояния от центра окружностей до оси ординат меньше радиуса, следовательно, обе
окружности берутся целиком.

Второе уравнение — окружность с центром и радиусом (назовем ее ).

Две окружности имеют одну общую точку, если они касаются внешним или внутренним образом. Следовательно, должна касаться
одним из двух способов с одной окружностью и вовсе не иметь общих точек с другой. Заметим, что расстояние от центра до первой
окружности меньше, чем до центра второй, следовательно, первое касание будет внешним с первом окружностью, затем внешнее со второй,
затем внутреннее с первой, затем внутреннее со второй. Следовательно, нам подходят только первый и четвертый случай:

∘------------
Q1O2 = (−6 +1)2+122 = 13
∘-----2----2 √---
O1O2 = (6+ 1)+ 12 = 193

Тогда

Ответ:

Найдите , при которых система

({ 4 2 2
x +y = a
( x2+y =|a+ 1|

имеет ровно четыре решения.

Показать ответ и решение

Пусть x2 = t , тогда t< 0 не дает решений , t= 0 дает одно решение x= 0 , t>0 дает два различных решения Система примет
вид

({ 2 2 2
t + y =a
(t+ y = |a+ 1|

Первое уравнение задает либо точку, либо окружность. Случай с точкой не подходит, потому как тогда смистема максимум может иметь
одно решение.

Тогда первое уравнение задает окружность с радиусом R = |a| , а второе — прямую. Окружность с прямой могут иметь 0, 1 или 2 точки
пересечения. Следовательно, чтобы после обратной замены мы получили четыре решения, необходимо, чтобы прямая имела с окружностью
две точки пересечения, абсциссы которых положительны.

Нам подходят все прямые между и .

Выше прямой AB : ;

ниже прямой CD : - - - -
|a+1|< EC =CD :√ 2= 2EF :√ 2= √2R =√ 2|a| .

Следовательно,

(
⌊ |||a< −1
||| {−a − 1 >−a
|| |||( √ -
||| (−a − 1 <− 2a
√- ({ || |||{−1 ≤a ≤0
|a|<|a+ 1|< 2|a| ⇔ (|a+1|> |a√| ⇔ ||| |a+ 1> −a
|a+1|< 2|a| || ||(a+ 1< −√2a
||| (|
|| ||{a> 0
|⌈ ||a+ 1> a-
|(a+ 1< √2a

Получаем ( ) ( )
a ∈ − 12;− √12+1 ∪ √12−-1;+∞ .

Ответ:

Найдите все значения параметра при каждом из которых уравнение

∘ -----------
ax+ −7− 8x− x2 = 2a +3

имеет единственное решение.

Показать ответ и решение

Перепишем уравнение в виде

∘----------
f(x)= 9 − (x+ 4)2 = −a(x− 2)+ 3= g(x)

Графиком является верхняя полуокружность окружности 2 2
y + (x+ 4) = 9, график представляет собой
пучок прямых, проходящих через точку A(2;3).

Положения прямой которые нам подходят:

когда прямая проходит через точку

когда прямая находится между прямыми, проходящими через точки и включая положение

Найдем значения параметра, соответствующие прохождению прямых пучка через точки B,C,D.

B :

C : 1
0= 9a+ 3 ⇔ a = −3

D :

Тогда исходное уравнение имеет единственное решение при

[ )
a∈ −1;− 1 ∪ {0}
3

Ответ:

[ 1)
a ∈ − 1;− 3 ∪{0}

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Обоснованно получены все значения: Ответ отличается от верного только исключением точки и/или включением точки	3

Обоснованно получены все значения:	2

Верно найдено одно или два из значений	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Найдите , при которых система

имеет ровно два различных решения.

Показать ответ и решение

Рассмотрим вторую скобку:

Следовательно, система равносильна:

(|| ⌊y = √12−-x2
||||| ⌈ 1 2
||{ y = −√4x + 3
|| x⁄= ± 2
||||| 12 − x2 ≥ 0
||( y = 1− 2a

Найдем те , при которых горизонтальная прямая имеет две точки пересечения со множеством

Заметим, что в силу симметрии полуокружности и параболы относительно оси ординаты точек и одинаковы, а также
одинаковы ординаты точек и . Прямая будет иметь с голубым графиком две точки пересечения, находясь в положении
, в положении и между положениями и , исключая положение .

Ищем ординату точек и B : ∘----√--2 √ --
y = 12− ( 2) = 10 .

Ищем ординату точек и D : 1 √- 2 5
y = −4 ⋅( 2) + 3= 2.

1
1− 2a =0 ⇔ a= 2 ;

q : 5 3
1− 2a = 2 ⇔ a =− 4 ;

;

√ -- 1−√10
1− 2a = 10 ⇔ a= --2-- ;

√ - 1−2√3
1− 2a= 2 3 ⇔ a = -2--- .

Следовательно, ответ (1−2√3 ) {1−√10} { 3 1}
a∈ --2--;− 1 ∖ --2-- ∪ − 4;2 .

Ответ:

Найдите все значения параметра , при каждом из которых система

(
{y = 2|x − |a||− 2a2
( 2 ( √ -)2
x + y + 5 ≤ 1

имеет единственное решение.

Показать ответ и решение

Будем решать задачу графически. Графиком уравнения является уголок,
получаемый из уголка (вершина которого находится в точке (0;0) )
сдвигом на |a| единиц вправо и на 2
2a единиц вниз. Следовательно, вершина
уголка — это точка с координатами и
Тогда зависимость между этими координатами следующая: причем
заметим, что Следовательно, правая ветвь параболы (то есть
часть параболы при x ≥0 ) — траектория, по которой движется вершина уголка
2
y = 2|x− |a||− 2a .

Графиком неравенства является круг (то есть окружность с внутренностью) с
центром в точке √ -
O(0;− 5) радиуса R = 1.

Система имеет единственное решение, когда уголок и круг имеют ровно
одну общую точку, то есть одна из ветвей уголка касается окружности
2 √- 2
x + (y+ 5) = 1, а вторая не имеет с окружностью общих точек.

Изобразим графики.

Заметим, что только левая ветвь (назовем ее лучом ) уголка может касаться
окружности. Ветвь задается уравнением y = −2x +2|a|− 2a2,
l или же
2
2x +yl− 2|a|+ 2a = 0, Запишем условие касания луча и окружности
через формулу расстояния от точки до прямой: если прямая задана уравнением
то расстояние от точки до нее вычисляется по
формуле

ρ(O,p)= |Ax0√+-By0-+C-|.
A2 + B2

Заметим, что при использовании этого способа найденные требуют
проверки, так как это условие задает касание прямой и окружности, а не луча и
окружности.

В случае касания левой ветви и окружности расстояние от центра
окружности до должно быть равно радиусу окружности:

ρ(O, l)= R ⇔

|−-√5−-2|a|+-2a2|
√22-+12- = 1 ⇔

|2a2− 2|a|− √5|= √5- ⇔

⌊ 2
⌈ 2a − 2|a|=√-0 ⇔
a2− |a|− 5= 0
⌊
a= 0
||
|| a= ±1
|⌈ ∘1--+4√5-+ 1
a= ±------2-----

Заметим, что a = 0 не подходит, так как в этом случае точка касания
находится не на луче (задаваемом уравнением ), а на его
продолжении за вершину уголка, то есть на луче при x > 0, а эти точки
не принадлежат уголку что видно из рисунка:

Следовательно, ответ:

{ ∘1-+-4√5+ 1 ∘1-+-4√5+ 1}
a∈ − -----2-----;−1;1;-----2------ .

Ответ:

{ ∘ ----√-- ∘ ----√-- }
--1+-4--5+-1 --1+-4--5+-1
a ∈ − 2 ;− 1;1; 2

Найдите все значения параметра , при каждом из которых система

(
{y = |x− a|+ a2
( 2 2
x + (y− 2) = 2

имеет единственное решение.

Показать ответ и решение

Будем решать задачу графически. Графиком первого уравнения является уголок,
получаемый из графика функции y =|x| (вершина которого находится в точке
(0;0) ) сдвигом на |a| единиц вправо, если a> 0, и влево, если a< 0, а затем
сдвигом на единиц вверх. Следовательно, координаты вершины уголка
— это x0 = a, Тогда между этими координатами
следующая зависимость: Это значит, что парабола y =x2 является
траекторией движения вершины уголка.

Графиком второго уравнения является окружность с центром в точке O (0;2)
радиуса √-
R = 2.

Система имеет единственное решение, если ровно одна из ветвей уголка
касается окружности, а вторая ветвь не имеет с окружностью общих точек.

Заметим, что окружность и парабола симметричны относительно оси ординат,
следовательно, если a≥ 0 и вершина уголка находится в первой четверти,
то если левая ветвь уголка касается окружности при a = a0, тогда при
(когда вершина уголка находится во второй четверти) правая
ветвь касается окружности. Значит, достаточно рассмотреть только случай
a ≥0.

Пусть

Левая ветвь (назовем ее ) уголка задается уравнением или
Запишем условие касания луча и окружности через
формулу расстояния от точки до прямой: если прямая задана уравнением
то расстояние от точки до нее вычисляется по
формуле

|Ax0 +By0 + C|
ρ(O,p)= --√A2-+-B2---

ρ(O, l)= R ⇔
2
|0-+√-2−-a−-a| =√2- ⇔
12+ 12
2
|a + a− 2|= 2 ⇔
⌊ a2 +a = 0
⌈ ⇔
a2 +a − 4= 0
⌊
a= 0
||
||⌈ a= −1 √ --
a= −1-±--17
2

Так как мы рассматриваем случай a ≥0, то нам подходят лишь
−-1+√17
a = 0; 2 . Но при a= 0 вершина уголка находится в точке (0;0) (см.рис.),
следовательно, уголок, как и окружность, симметричен относительно оси ординат,
значит, если есть точка касания уголка и окружности в первой четверти,
то есть и точка касания во второй четверти. Следовательно, при a= 0
уголок и окружность имеют две общие точки, что нам не подходит. Тогда
остается только одно значение параметра −1+√17
a= a0 = 2 , что соответствует
рисунку.

Значит, как говорилось выше, если a< 0 и вершина уголка находится во
второй четверти, то правая ветвь касается окружности при √--
a =− a0 = − −-1+217.

Следовательно, { 1−-√17-−-1+-√17}
a∈ 2 ; 2 .

Ответ:

{ √-- √--}
a ∈ 1−--17; −-1+-17
2 2

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточное обоснование построения	3

Получено верно одно из двух значений параметра	2
ИЛИ
Значения параметра найдены верно, но также в ответ записаны лишние значения параметра

Верно сведено к исследованию графически или аналитически, при этом построение обосновано	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Найдите все , для каждого из которых найдется такое , что система

(| 3
{x =|y− b|+ b
|(x2+ y2+32 =a(2y− a)+ 12x

имеет хотя бы одно решение (x;y) .

Показать ответ и решение

Исходная система имеет решения, если новая система (где поменяны местами переменные и )

(| 3
{y = |x− b|+ b
|(y2+ x2+32 =a(2x− a)+ 12y

также имеет решения.

Первое уравнение задает уголок, который строится последовательно следующим образом:

Вершина уголка x0 = b , 3
y0 = b , следовательно, она движется по гиперболе -3
y0 = x0 .

Второе уравнение при фиксированном задает окружность:

Центр этой окружности O(a;6) , а радиус R =2. Следовательно, при изменении центр окружности движется по
прямой y =6 . Значит, при всех это уравнение задает полосу . Таким образом, нам необходимо, чтобы
уголок находился в таком положении, когда существует хотя бы одна точка пересечения уголка с этой полосой (тогда
существует хотя бы одна окружность, с которой уголок имеет общие точки). На рисунке розовым цветом обозначено граничное
положение уголка, выше которого общих точек с полосой нет, а фиолетовым — промежуточные положения, когда общие точки
имеются:

Заметим, что если вершина уголка находится на ветви гиперболы, находящейся в III четверти, то уголок всегда пересекает полосу. Это
задается условием . Если же вершина уголка находится на ветви, лежащей в I четверти, то требуется найти розовое граничное
положение, когда вершина уголка лежит на верхней границе полосы, то есть в точке пересечения гиперболы y = 3x и прямой
y =8 :

(|{ 3 (|{ 3
y = x ⇔ x= 8
|(y =8 |( y = 8

Таким образом, при уголок имеет общие точки с полосой. Следовательно, ответ a< 0 или

Ответ:

a ∈(−∞;0)∪ [3;+∞ )
8

Найдите все , при которых уравнение

имеет
единственное решение.

Показать ответ и решение

Обозначим черех значение каждой из частей уравнения. Тогда оно эквивалентно системе

pict

Первая подсистема задает часть окружности с центром (3;a) и радиусом 1, лежащую не ниже прямой
y = a . Фактически это верхняя полуокружность такой окружности, т.к. горизонтальная прямая y = a
всегда проходит через ее центр. Центры всех таких полуокружностей лежат на горизонтальной прямой
x = 3 .

Вторая подсистема задает часть окружности с центром (a;3) и радиусом 1, лежащую не ниже прямой y = 3 .
Фактически это верхняя полуокружность такой окружности, т.к. горизонтальная прямая y = 3 всегда
проходит через ее центр. Центры всех таких полуокружностей лежат на вертикальной прямой y = 3 .

Синее положение достигается при a = 3 , полуокружности совпадают. Увеличение на положительное число
соответствует сдвигу одной полуокружности на вверх, а другой вправо. При уменьшении аналогично вниз и
влево.

Крайние положения, в которых еще есть точка пересечения, достигаются при сдвиге на − 1 и + 1 относительно
a = 3 , то есть при a = 2 и a = 4 .

При a > 4 зеленая полуокружность будет целиком лежать выше прямой y = 4 , а значит, гарантированно не будет
иметь точек пересечения с красной полуокружностью.

При a < 2 зеленая полуокружность будет целиком лежать ниже прямой y = 3 , а значит, гарантированно не будет
иметь точек пересечения с красной полуокружностью.

В любом положении между крайними, кроме синего, будет одна точка пересечения. Действительно, все такие точки
пересечения будут лежать на отрезке между точками (3;3) и (4;4) . Получаем .

Ответ:

Найдите все значения при каждом из которых система уравнений

({ 2 2
(x − a) + y = 1
( y = |x − 3|+ 12

имеет ровно одно решение.

Показать ответ и решение

Рассмотрим первое уравнение. Оно задает окружность в системе координат xOy с
центром в точке O (a;0) и радиусом 1. Другими словами, это семейство
окружностей с радиусом 1 и центром в произвольной точке прямой y = 0 (то есть
оси абсцисс).

Второе уравнение задает «уголок» модуля с ветвями вверх и вершиной в точке
( )
3; 1 .
2 Левая ветвь содержится в прямой правая — в прямой

Построим графики.

Заметим, что если окружность с центром в точке нам подходит
(то есть имеет ровно одну точку пересечения с уголком), то и окружность,
симметричная ей относительно прямой x= 3 (эта прямая — ось симметрии
уголка) с центром в точке нам тоже подойдет. Более
того, очевидно, что никакие другие окружности не подойдут. Осталось понять, при
каких (то есть центр не правее оси симметрии) окружность имеет ровно
одну точку пересечения с левой веткой уголка. Часть решения ниже, выделенная
курсивом, нужна исключительно для неформального понимания задачи, на
экзамене так писать не следует.

Представим нашу ситуацию следующим образом. У нас есть окружность
фиксированного радиуса, центр которой «скользит» по оси абсцисс. Давайте
двигать окружность из − ∞ вправо до тех пор, пока она не «упрется» в
уголок (или, другими словами, пока не соприкоснется с уголком). В этот
момент окружность либо будет касаться (прямая будет касательной к
окружности) левой ветки уголка, либо «упираться» в точку — вершину уголка
(при этом прямая не будет являться касательной к окружности!).

Во втором случае момент касания с прямой происходит раньше, чем момент
касания с уголком (и только при движении дальше вправо мы упираемся в
вершину уголка), так как касание происходит в точке, принадлежащей
продолжению прямой (пунктирная часть).

Найдем положение касания с окружности с прямой
содержащей левую ветвь уголка. Если точка касания окружности и прямой будет
лежать левее вершины уголка (т.е. координата точки касания по оси не
больше, чем 3) — реализовалась первая ситуация, в противном случае
реализовалась вторая.

Радиус окружности равен единице, значит, в моменте касания центр
окружности лежит на расстоянии 1 от прямой Построим прямую левее
параллельную на расстоянии 1 от Искомое положение окружности
возникает, когда центр окружности попадает в точку O
1 пересечения прямой и
оси абсцисс, по которой движется центр.

Пусть — точка пересечения с осью абсцисс, — точка касания
окружности и прямой и равен расстоянию между прямыми — это 1
по построению. так как коэффициент при равен
− 1. Тогда в полученном равнобедренном прямоугольном треугольнике
√-
O1M = 2 и координата по точки равна √ -
3,5 − 2, а координата по
точки касания равна √-
3,5 − 22. Легко проверить, что это меньше, чем 3 —
координата по вершины уголка и оси симметрии, значит, реализована первая
ситуация (касание с левой веткой). Итого нам подходит √-
a= 3,5− 2,
которому соответствует положение центра, а также √ -
a = 2+ 2,5,
которому соответствует симметричное относительно оси положение центра —
O2.

Таким образом,

Ответ:

{ √ -√ - }
a ∈ 3,5− 2; 2+ 2,5

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточно обоснованное построение	3
ИЛИ
недостаточно обоснован какой-либо момент при исследовании	3

Верно рассмотрен один из двух случаев и найдено одно из значений параметра	2
ИЛИ
верно проанализированы оба случая, но в ходе решения значения параметров найдены неверно

Задача верно сведена к исследованию графически, выполнено верное построение с обоснованием	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Источник

Материалы
для занятия по теме

«Параметр
в уравнении окружности»

1.Уравнение окружности.

(х ‒ х₀)² + (у ‒ у₀)²
= R²,
где А(х₀; у₀) ‒ центр окружности, R
‒ радиус.

х² + у² = R²
‒ уравнение окружности с центром в начале координат.

2.Параметр – радиус.

(х ‒ х₀)² + (у ‒ у₀)²
= а

Если а = 0, то (х ‒ х₀)² + (у‒ у₀)²
= 0, то есть А(х₀; у₀) – точка.

Если а ˂ 0, то ни окружность, ни точка не
существуют.

Если а > 0, то R =, на плоскости –
концентрические окружности с центром (х₀; у₀).

Пример. (х ‒ 2)² + (у + 2)² = а (а > 0)

3.Параметр в одной из координат центра.

Одна координата с
параметром: (х ‒ 2а)² + (у + 3)² = 9. У центра окружности меняется абсцисса,
ордината постоянна. Значит, центры окружностей зафиксированы на прямой у =
‒3.

Задание:
подставляя разные значения параметра а, определите координаты центров
нескольких окружностей и выполните построение.

Аналогично: (х‒3)² +(у ‒ 2а)² = 9. У
центра окружности меняется ордината, абсцисса постоянна. Центры окружностей
зафиксированы на прямой х=3.

Задание: построить несколько окружностей,
удовлетворяющих последнему уравнению.

4. Параметр в обеих координатах центра.

(х ‒ а)² + (у ‒ а)² = 1. Обе координаты с
параметром.

Центр окружности ‒ точка А (а ; а). Так
как абсцисса и ордината равны, то все точки такие находятся на прямой у = х.
Тогда данное уравнение задает множество окружностей , центры которых лежат на
прямой у = х , а радиус равен 1.

Задание:
построить несколько окружностей, удовлетворяющих следующему уравнению (х ‒ а)²
+ (у + 2а)² = 4.

Подсказка. Найдем координаты центра
окружности: (х ‒ а)² + (у ‒ (‒2а))² = 4

А(а;-2а), значит центры окружностей лежат
на прямой у = ‒2х, радиус равен 2.

5.Параметр в координатах центра и в
радиусе.

( х ‒ а)² + (у‒ 2а ‒1 )² = а². Это
окружности с центрами на прямой у = 2а + 1, радиус равен а. При а=0 – точка.

Задания
для самостоятельной работы.

№1. Указать центр, радиус и построить
каждую окружность , заданную уравнением:

а) (х ‒ 3)² + (у + 2)² = 16; б) (х + 1)² +
(у ‒ 4)² = 10.

№2. Выяснить, какие из данных уравнений
являются уравнениями окружности. Найти координаты центра и радиус каждой
окружности:

а) х² + у² + 8х ‒ 4у + 40 = 0;

б) х² + у² ‒ 2х + 4у ‒ 20 = 0;

в) х² + у² ‒ 4х ‒ 2у + 1 = 0.

№3. Выделить уравнение окружности, указать
ее центр и радиус в задачах с параметром. Описать расположение графика
уравнения на координатной плоскости. Выполнить построение:

а) х² + у² + 2ах ‒ 4у + а² ‒ 1 = 0;

б) х² + у² ‒ 6х + 4ау + 4а² = 0;

в) х² + у² ‒ 2а( х ‒ у ) = 4 ‒ 2а².

Литература:

1.Геометрия. 7-9 классы : учебник для
общеобразовательных организаций с приложением на электронном носителе / [Л.С.Атанасян,
В.Ф.Бутузов, С.Б.Кадомцев и др.]. – 3-е изд.-М. : Просвещение, 2014.-383 с.

2.Шестаков С.А. ЕГЭ 2014. Математика.
Задача С5. Задачи с параметром / Под ред. А.Л.Семенова и И.В.Ященко. –
М.:МЦМНО. 2014.-240 с.

Источник

Задания с параметрами, окружности

Задания с параметром
Окружности

ВВЕДЕНИЕ
Задания с параметрами представляют наибольшую трудность у выпускников школ. В учебных программах по математике общеобразовательных школ задачам с параметрами отводится незначительное место.
Эти задачи обладают высокой позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности. Решение задач с параметрами требует наличия определенной математической культуры.
В данной работе представлены материалы по теме «Решение задач с параметром в 7-9 классах».
Эту работу можно использовать на уроках алгебры как в классах с базовым уровнем, так и в классах с расширенным или углубленным изучением алгебры. Работа будет интересна учителям при объяснении нового материала, а также при формировании навыков решения задач с параметром.
Для учащихся эта работа может быть пособием при самостоятельном изучении данной темы.

Существуют два основных способа решения заданий с параметрами: аналитический и графический.
В моей работе упор сделан на графическом способе, причем показать примеры решения задач, в которых присутствуют системы уравнений или неравенств с окружностями. Были использованы различные ресурсы, в которых были разобраны задания с параметром.
В работе представлены графические способы решения систем уравнений и неравенств с параметром.
Для того, чтобы научиться решать такие задания, необходимо иметь хорошую базовую подготовку по основному школьному курсу, знать алгоритмы решения заданий с параметрами.
Какими знаниями и умениями нужно обладать, прежде чем начать решать такие задания?

Нужно знать «в лицо» все элементарные школьные функции, уметь изображать решения уравнений и неравенств в координатной плоскости.
Нужно уметь строить семейства различных линий:
у = kх + а, у = х + а, у = ах, у = |x| + a; y =
3) Уметь производить преобразования графиков (параллельный перенос вдоль координатных осей, растяжение и сжатие).

Алгоритм решения задач с параметром графическим методом заключается в следующем:

Преобразовываем исходное условие задачи к системе уравнений или неравенств для того, чтобы можно было изобразить графически решения уравнений или неравенств.
Найти область допустимых значений переменной и параметра.
Вводим систему координат (х; у) или (х; а).
Изображаем в выбранной координатной плоскости фигуру, которая задается множеством решений уравнения или неравенства или их системы.
Проанализировать изменения графиков в зависимости от параметра.
Записать ответ, удовлетворяющий условию задачи.

Перед разбором заданий предлагаю подготовительную работу – познакомиться с еще некоторыми видами линий и множеством точек.

1. Уравнение   задает окружность с центром в начале координат и радиусом .

2. Уравнение   задает окружность с центром в точке (a; b) и радиусом .

3. Неравенство      задает
круг вместе с границей.

4. Множество точек, лежащих вне круга, задается неравенством

5. Уравнение   задает верхнюю полуокружность с центром в начале координат и радиусом

6. Уравнение  задает нижнюю полуокружность с центром в начале координат и радиусом

7. Уравнение   при положительных a, b и c задает ромб с центром в начале координат (, ; диагональ лежит на оси ординат, диагональ лежит на оси абсцисс).

8. Уравнение   при положительном с задает квадрат с центром в начале координат (d = 2c).

Задание 1. При каком значении параметра , система
имеет единственное решение?

(1)
(2)
(1):
– квадратичная функция, график – парабола с вершиной (1;1),
ветви которой направлены вверх.

(2):
Уравнение описывает окружность с центром (1;), радиусом, равным 1.

Система имеет столько решений, сколько общих точек имеют графики. Графики могут не иметь общих точек, иметь одну, две или три общие точки. Выберем то значение параметра а, при котором графики одну общую точку, а значит, система имеет единственное решение.
Ответ: .

Решение:
РАЗБОР ЗАДАНИЙ уровня ЕГЭ

Задание 2. Найдите все положительные значения а, при каждом из которых система
имеет единственное решение.

1) Если
(5;4) и радиусом, равным 3.

2) Если
(5;4) и радиусом, равным 3.

(1)
(2)
3) Если
(;0) и радиусом, равным а.

(3)
Решение:

Исходная система имеет единственное решение тогда и только тогда, когда окружность (3)
касается ровно одной из двух окружностей (1) или (2) и не пересекается с другой.

При а < окружности (1) и (3) не пересекаются;

При а = или а = эти окружности касаются.

При <a< окружности (1) и (3) имеют две общие точки.

Ответ: 2; .

2)

При а < окружности (2) и (3) не пересекаются;

При <a< окружности (2) и (3) имеют две общие точки.

При а = или а = эти окружности касаются.

Исходная система имеет единственное решение тогда и только тогда, когда окружность (3) касается ровно одной из двух окружностей (1) и (2), то условию задачи удовлетворяют только числа а = 2 и а = .

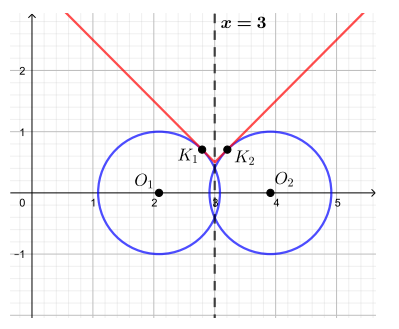
Задание 3. При каких значениях параметра система

имеет единственное решение?
(2) Графиком функции у = |х – 1| + а является угол с вершиной (1; а), стороны угла – лучи, угловые коэффициенты которых равны 1 и 1.

(1)
(2)
(1): Графиком уравнения
(|х| – 4)2 + (у – 3)2 = 2 являются две окружности:
с центром (4; 3) и R =
с центром (4; 3) и R = .

Найдем значения параметра а, при которых графики имеют одну общую точку, а значит, система имеет единственное решение.
Ответ: а = 4; а = 2.

Решение:

Задание 4. При каких значениях параметра а система уравнений
не имеет решений?

3
5
4
2
х
у
0
Ответ: а≠3

График первого уравнения – окружность с плавающим
центром (2; а), радиусом, равным 2.
График второго уравнения – окружность с центром (5; 3), радиусом, равным 1.
Для того, чтобы система не имела решений, нужно, чтобы окружности не имели общих точек.
Они могут иметь только лишь одну общую точку в случае касания, когда а = 3, поэтому система не имеет решений при любом значении а, не равном 3.
Решение:

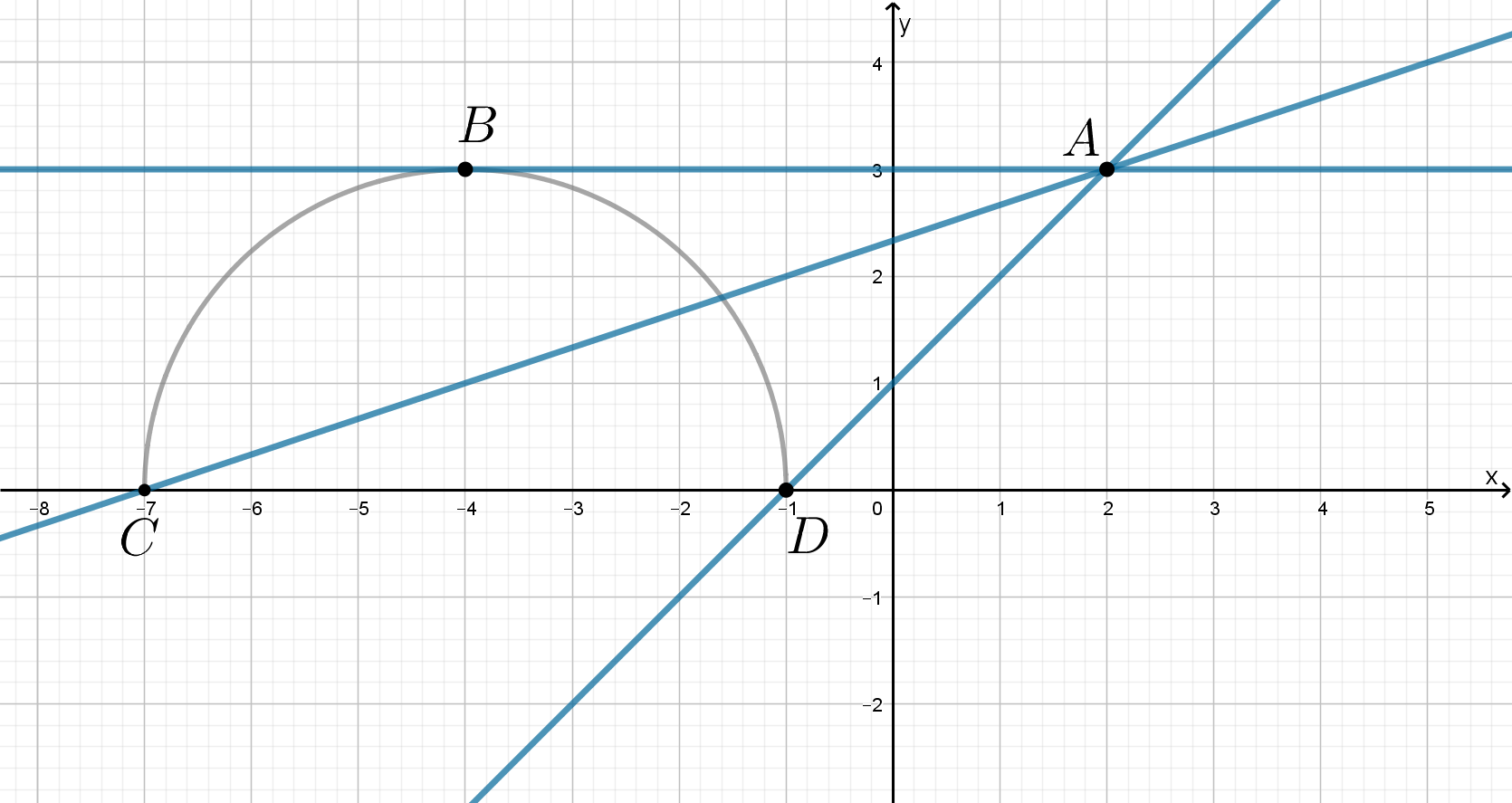
Задание 5. Найдите все значения a, при каждом из которых уравнение
имеет ровно один корень.

Рассмотрим две зависимости:
у = (1) и у = (2).

(1): у =

Полуокружность, центр (1; 0), радиус = 2.

(2): у = + 4а + 2

у = 4) + 2 семейство прямых с угловым коэффициентом,
равным (а), проходящих через точку (4; 2).

Решение:
Единственный корень будет в уравнении, когда прямая будет являться касательной к полуокружности, или проходит между прямыми МА и МВ.
1) В случае касания угловой коэффициент прямой равен 0.
2) Для того, чтобы данная прямая проходила между прямыми МА и МВ, нужно, чтобы , где – угловой коэффициент прямой МА, вой коэффициент прямой МВ.

МА: точки (4; 2) и (3; 0), =

МВ: точки (4; 2) и (; 0), =

Т.е. , значит а

Ответ: а

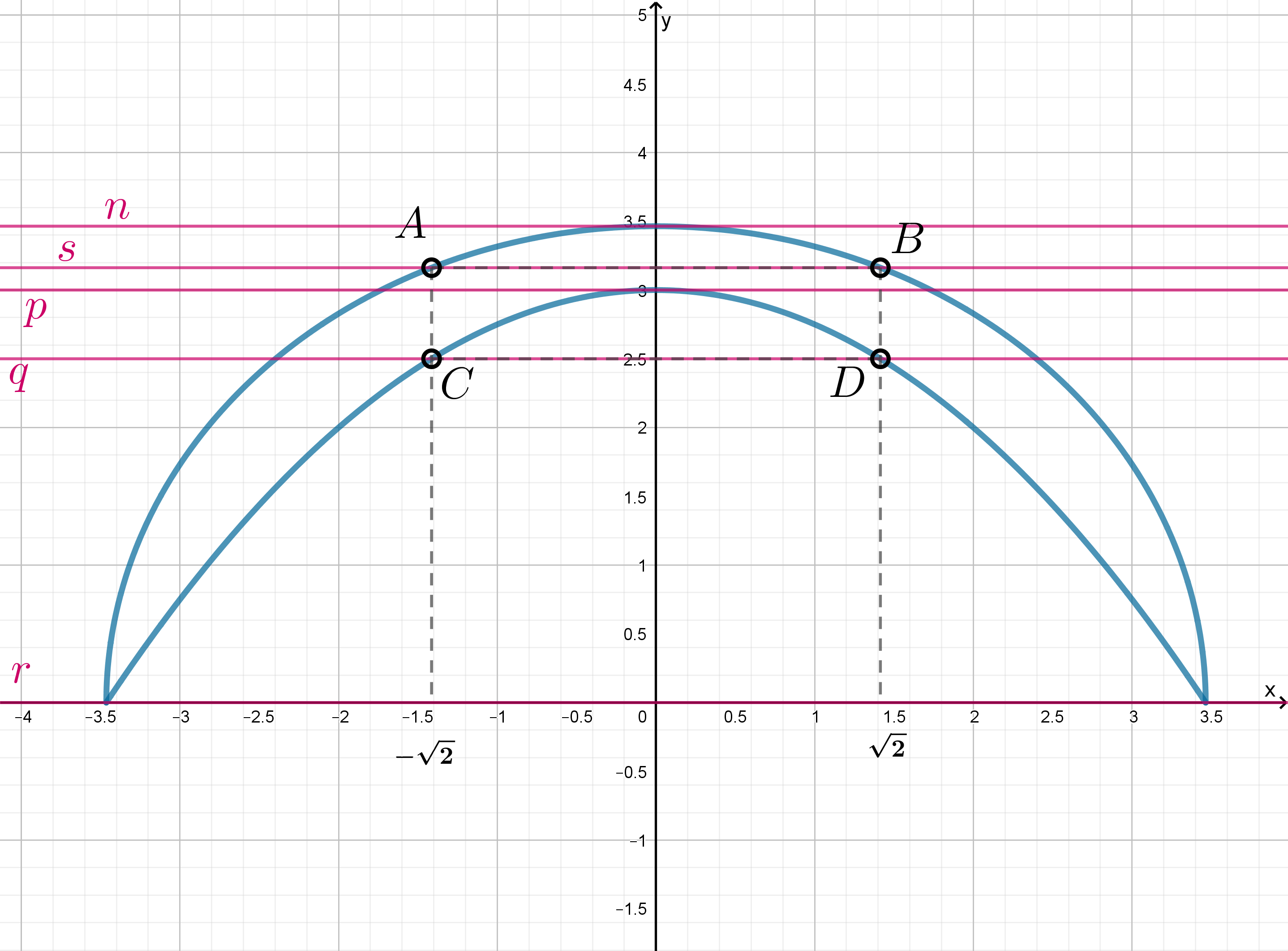
Задание 6. Найдите все значения a, при каждом из которых система уравнений
имеет ровно три решения.

(1):
1) Если х > 0, то

(1)
(2)

)=0

График – окружность, центр (0;2), радиус = 2
2) Если х = 0, то равенство верно, т.е.
График – множество точек, у которых х = 0
3) Если х < 0, то

)=0

График – окружность, центр (0;0), радиус = 4
(*)
(**)
Решение:
(2): а

Семейство прямых, параллельных прямой у = х

Для того, чтобы система имела 3 решения, нужно, чтобы прямая y = x + a пересекала график первого уравнения ровно в трех точках.
Рассмотрим случаи:

когда прямая y находится между I и II (не включая эти случаи).
Положение I – касание прямой y и окружности (*).
Положение II – прохождение прямой y через точку пересечения окружности (*) и прямой x=0.

Пусть A(0;a), B(−a;0) – точки пересечения y с осями координат, K – точка касания.
Тогда OK⊥AB (как радиус, проведенный в точку касания).
OA=a, OB=a, OK=4. △AOB прямоугольный. Тогда AB=.
S△AOB=0,5OK⋅AB=0,5OB⋅OA;

Таким образом, а =
Найдем значение a, при котором прямая y находится в положении II.
В этом случае y проходит через точку (0;4), следовательно, 4 = 0 + a, а = 4.
Таким образом, в случае (1) a∈(4; ).

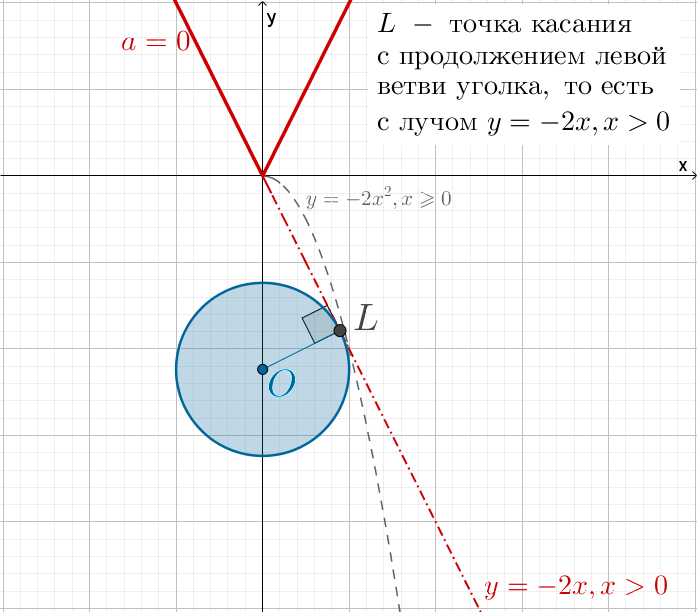
2) когда прямая y находится между II и III (не включая II и включая III)
Положение III – прохождение прямой y через точку пересечения окружности (**) и прямой x=0
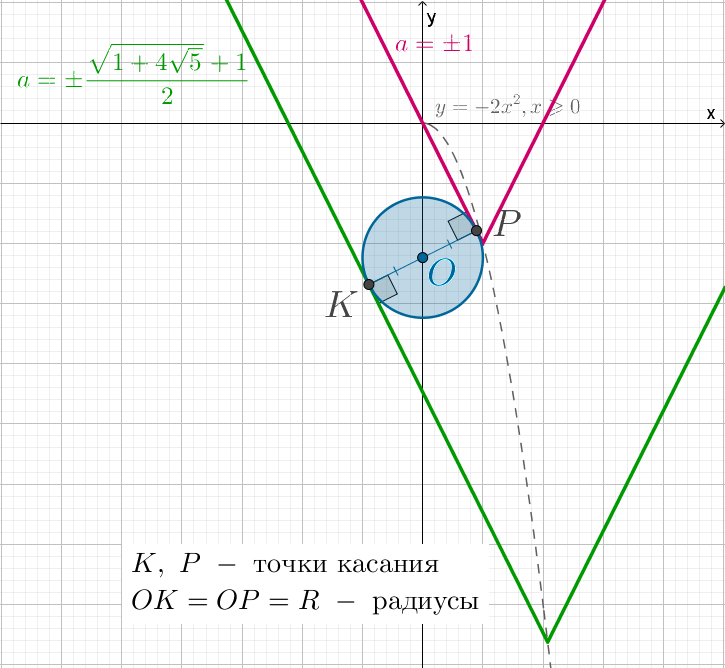
3) когда прямая y находится в положении IV – касается окружности (**).

Найдем a, при котором прямая y находится в положении III.
В этом случае она проходит через точку (0;0), то есть a=0. Таким образом, a ∈ [0; 4).

В этом случае a<0.
Пусть Q – центр окружности s, P – точка касания, C – точка
пересечения y с осью ординат.
Тогда △QPC – прямоугольный. ∠QCP=45∘.
Радиус QP=2, OC = −a (так как a<0), QO=2.

Отсюда а =

Ответ:

0

Задание 7. Найдите все значения а, при каждом из которых уравнение
имеет ровно один корень на отрезке

Решение.
Условие:

Таким образом, все решения уравнения находятся
внутри круга с центром в точке (5; 0) и радиусом,
равным 5.
Условие равенства дроби нулю:

0
А
В
С
D
E
Уравнение имеет ровно один корень на отрезке

Ответ:

Задание 8. Найдите все значения параметра a, при каждом из которых система имеет единственное решение.
Решение.

При a=−1 второе уравнение задает точку (−3;−1),
координаты которой не являются решением первого
уравнения. Следовательно, при a=−1 система не имеет
решений, значит, a=−1 не подходит.
(1): график первого уравнения – окружность с центром
О (2а – 3; а), радиус = 1,5
(2):

При а

Рассмотрим случай, когда a≠−1.
Система будет иметь единственное решение, когда окружности будут касаться друг друга (внутренним или внешним образом).
Центры обеих окружностей находятся на прямой y=a. То есть линия центров окружностей параллельна оси абсцисс.

1) Пусть окружности касаются внешним образом в точке K. Может быть один из двух случаев:

Расстояние между центрами окружностей равно сумме радиусов, т.е. QO =

С другой стороны, QO =

Получим уравнение:

Решениями этого уравнения являются значения а: , а = 2,5

2) Пусть окружности касаются внутренним образом в точке K. Может быть один из двух случаев (а также симметричные рисунки, то есть когда точка касания находится слева):

В этом случае QO равно разности радиусов, т.е.

Получим уравнение:

Из этого уравнения получаем, что а =

Ответ:

Задание 9. Найдите все значения параметра a, при которых система
имеет единственное решение.

(1)
(2)
(1):

Первый множитель неотрицателен. Он обращается в нуль при х = 1, у = 1

Следовательно,

Решение.
Т.е.

Таким образом, графиком первого уравнения являются две области и точка (1; 1)

(2):

При а + 4 > 0 график – окружность с центром (2; 0) и радиусом

При а = 4 получится точка (2; 0), но она не попадает в области, заданные неравенством (1).

Система будет иметь единственное решение тогда и только тогда, когда окружность будет иметь ровно одну общую точку с областью.
Это возможно в одном из двух случаев:

Если окружность коснется границы области y=−2x+8.
Окружность проходит через точку (1; 1)

1 случай:
Если окружность коснется границы области y=−2x+8.
Пусть P – точка касания, значит OP⊥ прямой y=−2x+8).
Рассмотрим прямоугольный △OPQ, где Q(4;0) – точка пересечения прямой y=−2x+8 с осью абсцисс.
Угловой коэффициент прямой = -2
А

OP =

OP=R=

, отсюда а =

2 случай:
Окружность проходит через точку (1; 1)

Значит, а = 2

Расстояние между точкой О и (1; 1) равно радиусу:

По формуле расстояния между точками расстояние между точкой О (2; 0) и (1; 1) равно

Получим уравнение:
Ответ:

Задание 10. Найдите все значения параметра a, при каждом из которых система уравнений имеет более двух возможных решений.

(1)
(2)
(1):

(*)
(**)
Решение:
(*):
(= 17

окружность с центром (4; 4), радиусом

С учетом условия (получится дуга с
концами в точках (5; 0) и (0; 5)

(**):

(= 97

окружность с центром (4; 4), радиусом

С учетом условия (получится дуга с концами в точках (5; 0) и (0; 5)

(2): прямая у = ах 5 проходит через точку (0; 5)

При а = 1 прямая проходит через точки M и N, тогда система имеет 2 решения
При а > 1 прямая имеет с дугами общую точку М.
Найдем значения а, при которых прямая касается окружности
с центром в точке В (точка касания – точка М). Тогда прямая

У перпендикулярных прямых произведение угловых коэффициентов
равно 1 (

Угловой коэффициент прямой ВМ равен , тогда

При этом прямая будет иметь с дугами две общие точки, т.е. в системе
2 решения.
При а < у прямой с меньшей дугой общая точка М, а с большей точка М и еще не более одной общей точки, значит система имеет не более двух решений.

При <a<1 прямая имеет с дугами по две общие точки, одна из
которых точка М.

Ответ: <a<1

Задание 11. При каких значениях параметра а система уравнений
имеет ровно 4 различных решения?
Пусть х – 2 = t, y + 3 = m, тогда

(*)

Решение:
m
Графики уравнений пересекаются в 4-х точках, когда
Окружность вписана в ромб, либо ее радиус

Высота (радиус окружности) прямоугольного
треугольника с катетами 8 и 15 равна .

, т.е.

2)

Ответ:

Задание 12. Найдите все значения параметра a, при которых система
имеет ровно два решения.

Т.к. 0, то рассмотрим 2 ситуации:

x < 0, y > 0
x > 0, y < 0

1 случай: x < 0, y > 0

График – окружность, центр (3; 2), радиус = 1

2 случай: x < 0, y > 0;

График – окружность, центр (3; 2), радиус = 1

(*)
(**)
Решение:
Уравнение у = ax + 1 задает семейство прямых, проходящие через точку (0;1):

Для того, система имела два решения, существуют 2 случая:

прямая пересекает одну окружность, а вторую – нет;
прямая касается обеих окружностей.

Так как окружности расположены симметрично относительно начала координат, то для того, чтобы прямая могла одновременно касаться обеих окружностей, она должна проходить через начало координат (то есть она тоже должна быть симметрична относительно начала координат). Прямая у = ах + 1 через начало координат не проходит. Следовательно, она не может касаться обеих окружностей сразу.
Значит, случай 2) невозможен.

Прямые (1) и (2) касаются окружности (*) с центром в точке

Найдем значения а для прямой (1):

Так как прямая и окружность касаются, то есть имеют одну точку пересечения, то полученное уравнение должно иметь один корень, следовательно, его дискриминант должен быть равен нулю:
D =

D = 0, если а = 0; а =

Для выполнения условия прямая у = ах +1 должна находиться между прямыми (4) и (1) или между прямыми (3) и (2)
Прямые (3) и (4) касаются окружности (**) с центром в точке

Найдем значения а:

D =

D = 0, если

Ответ:

Задание 13. Найдите все значения параметра a, при которых система
имеет ровно один или два решения

(1)
(2)
(1): 7

Если

Окружность с центром (0; 1) и радиусом

Если

, отсюда

Таким образом,

Решение:
(2): 3у = 2х + а;
у = х + – семейство параллельных прямых с угловым коэффициентом, равным

Найдем координаты точек пересечения прямых у = х и у = 2 – х с окружностью.
А(3; 3), В(– 2; – 2); С(– 2; 4); D(3; – 1)
C
M
Найдем координаты точки М – точки касания прямой 3у = 2х + а
с окружностью.

13

D = 160)

D = 0, если а = 16; а =

Т.к. а < 0, то для точки М значение а = 10.

М(2; 2)

Подставляя координаты точек А, В и D, найдем соответствующие значения параметра а.
Для точки А: а = 3
Для точки В: а = 2
Для точки D: a = 9

Одно или два решения будет в системе, если прямые
попадают в «розовую» область.
Ответ:

Источник

Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.

Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.

Вот список тем, которые стоит повторить:

1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».

2. Преобразование графиков функций.

3. Построение графиков функций.

4. Базовые элементы для решения задач с параметрами.

Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.

Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).

1. При каких значениях параметра a уравнение $frac{x^2+a^2-4a}{x-a}=0.$ имеет ровно 2 различных решения?

Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.

Получим систему:

$left{ begin{array}{c}x^2+a^2-4a=0 \x-ane 0 end{array}right.$

В первом уравнении выделим полный квадрат:

$x^2+{(a}^{ }-2)^2=4$

Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.

Уравнение a= x задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.

Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.

Кроме того, точка не должна лежать на прямой a= x , которая пересекает окружность в точках A(0; 0) и Координаты этих точек легко найти, подставим a= x в уравнение окружности.

Точка С также не подходит нам, поскольку при a = 4 мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.

Это значит, что

2. Найдите все значения a, при которых уравнение имеет единственное решение.

Уравнение равносильно системе:

$left{ begin{array}{c}a-2xy={left(y-x+7right)}^2 \y-x+7ge 0 end{array}right.$

Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).

Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.

$left{ begin{array}{c}a-2xy=y^2+x^2+49+14y-14x-2xy \yge x-7 end{array}right.$

Приводим подобные слагаемые в уравнении.

$left{ begin{array}{c}a=y^2+x^2+49+14y-14x \yge x-7 end{array}right.$

Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:

$left{ begin{array}{c}a+49={x^2-14x+49+y}^2+14y+49 \yge x-7 end{array}right.Longleftrightarrow left{ begin{array}{c}{left(x-7right)}^2+{left(y+7right)}^2=a+49 \yge x-7 end{array}right.$

Решим систему графически:

Уравнение ${left(x-7right)}^2+{left(y+7right)}^2=a+49$ задает окружность с центром в точке , где радиус

Неравенство yge x-7 задает полуплоскость, которая расположена выше прямой y=x-7 , вместе с самой этой прямой.

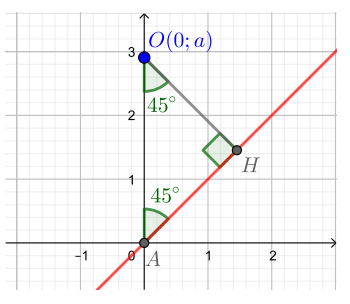
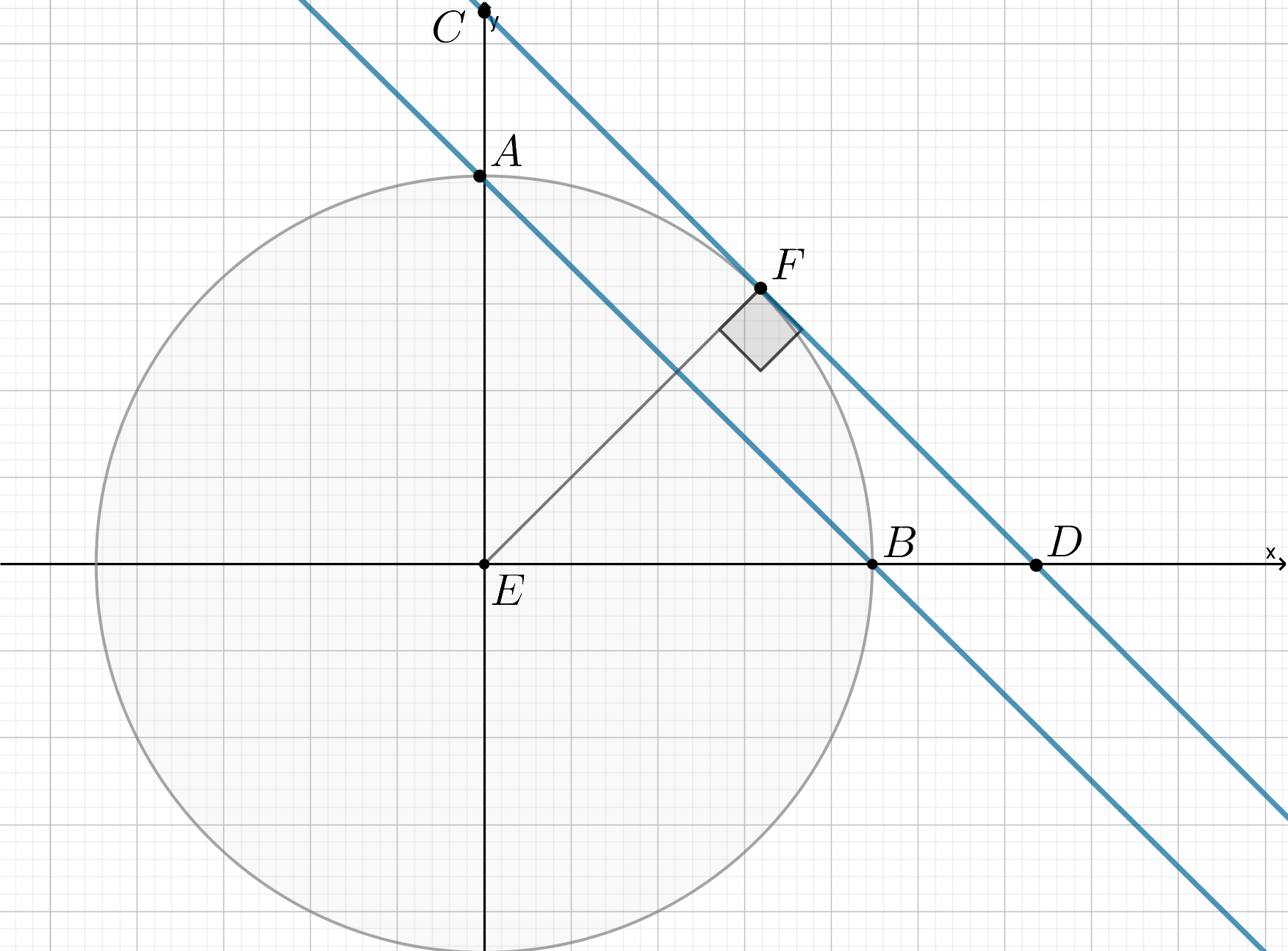
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением y= x-7.

Пусть С — точка касания.

На координатной плоскости отметим точки и , в которых прямая y= x-7 пересекает оси Y и Х.

Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит $PC=frac{AB}{2}$ по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.

Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.

$AB=sqrt{{AP}^2+{BP}^2}$

$AB=sqrt{7^2+7^2}=sqrt{98}=7sqrt{2}.$ Тогда

$PC=frac{AB}{2}$

$sqrt{a+49}=frac{7sqrt{2}}{2};$

Решая это уравнение, получаем, что

Ответ:

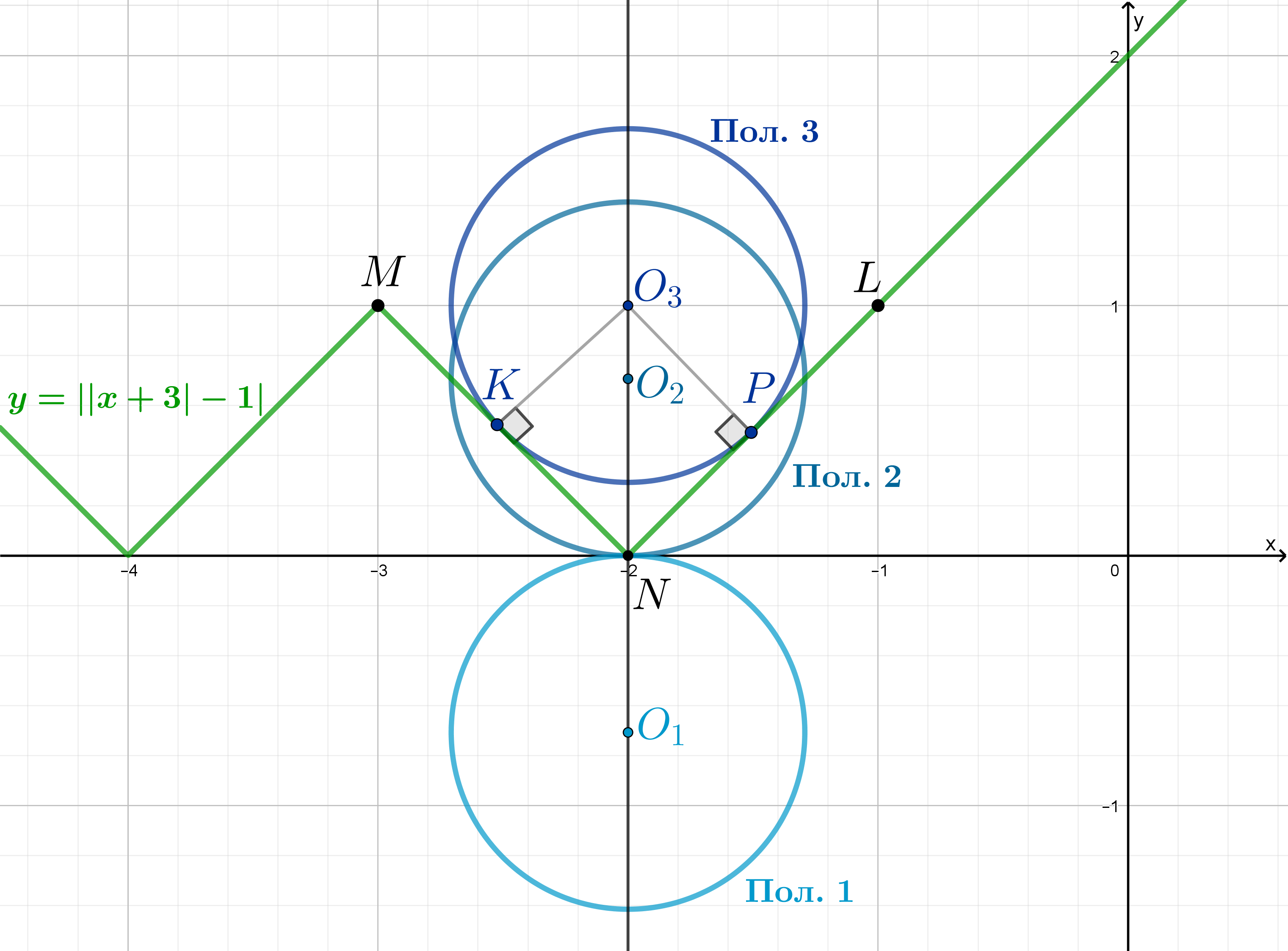
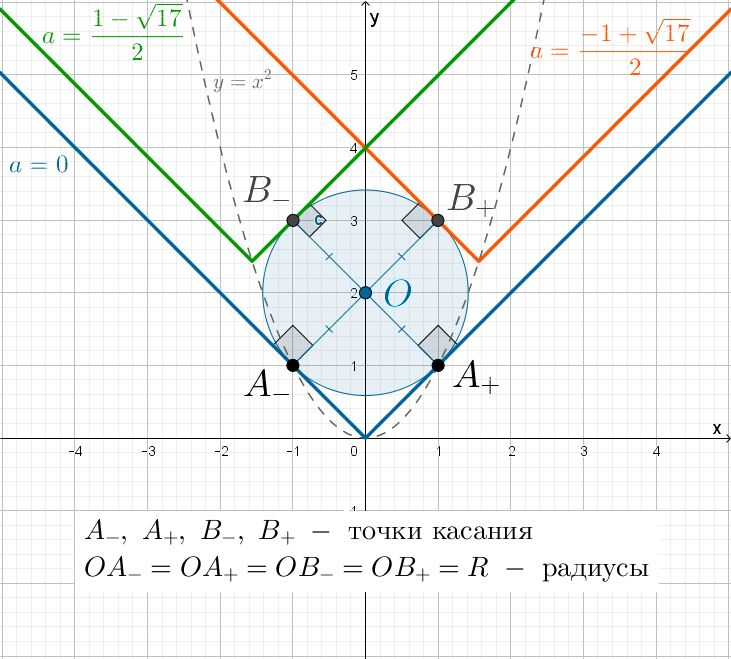
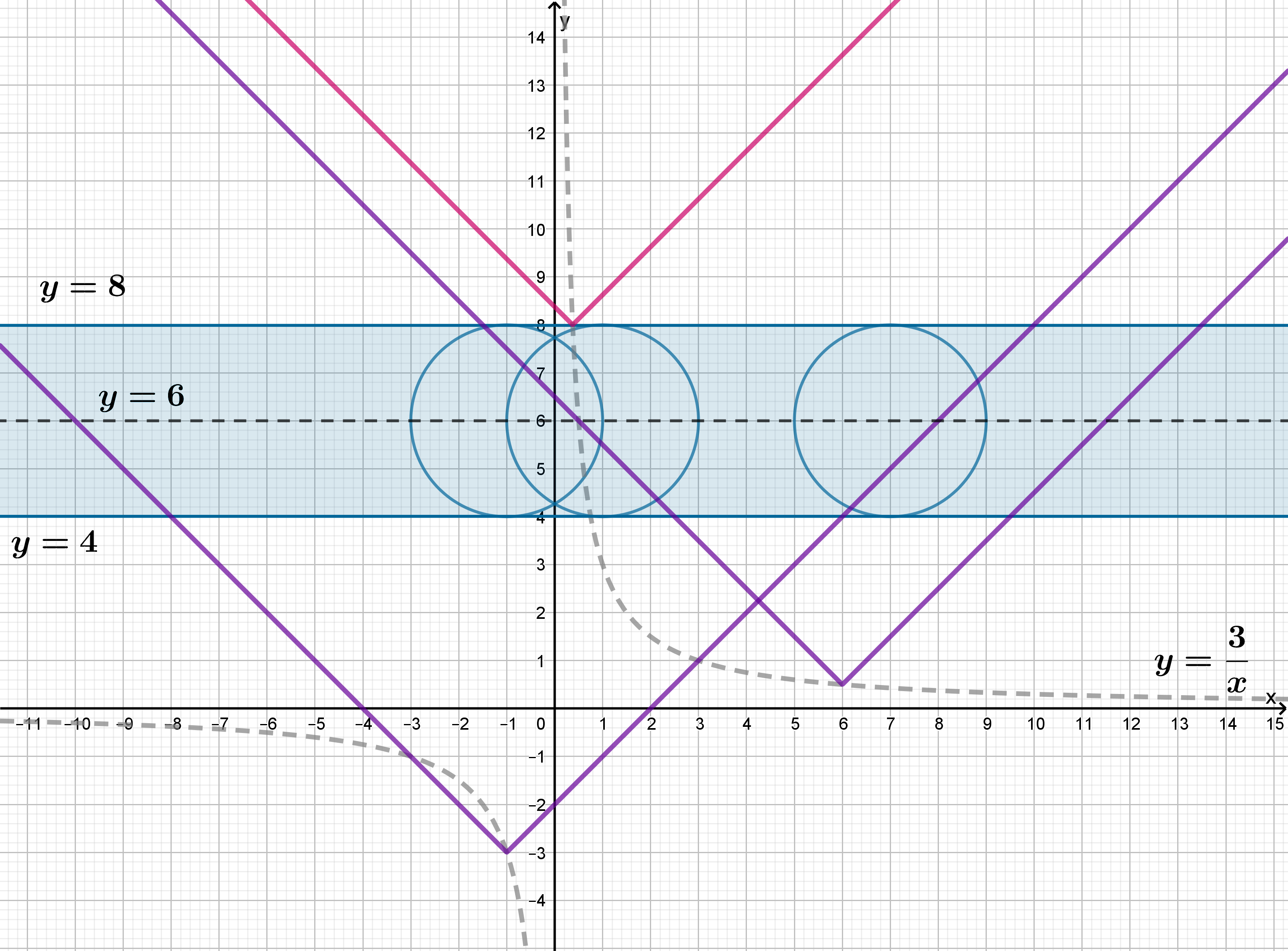
3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.

$left{ begin{array}{c}{(left|xright|-5)}^2+{(y-4)}^2=4 \{(x-2)}^2+y^2=a^2 end{array}right.$

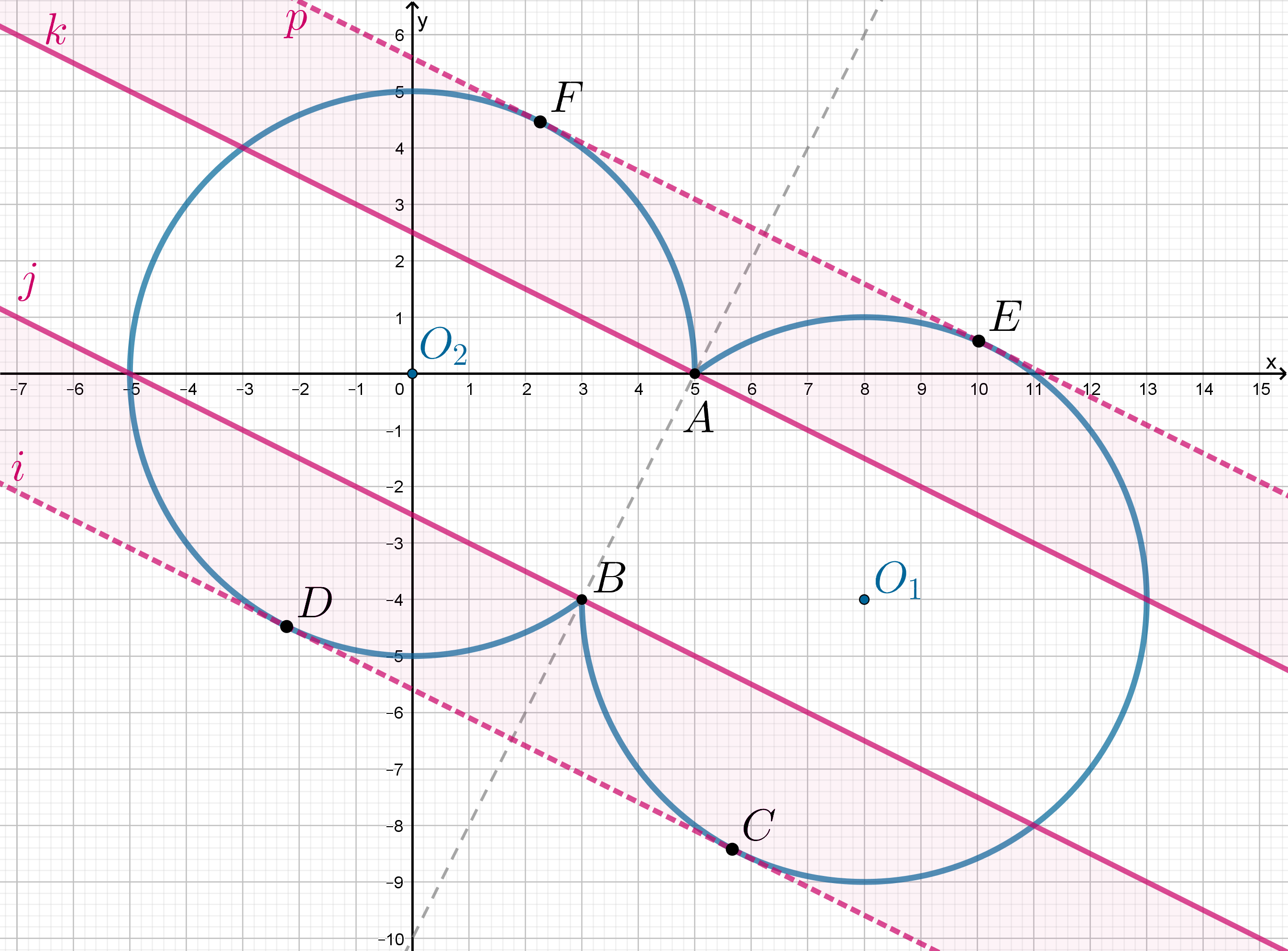
График уравнения ${(x-5)}^2+{(y-4)}^2=4$ – окружность с центром P (5;4) и радиусом равным 2.

График уравнения ${(left|xright|-5)}^2+{(y-4)}^2=4$ – две симметричные окружности и радиуса 2 c центрами в точках P (5;4) и Q(-5;4)

Второе уравнение при задает окружность omega с центром в точке M(2;0) и радиусом a.

Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.

Система имеет единственное решение в случаях, когда окружность omega , задаваемая вторым уравнением, касается только левой окружности или только правой

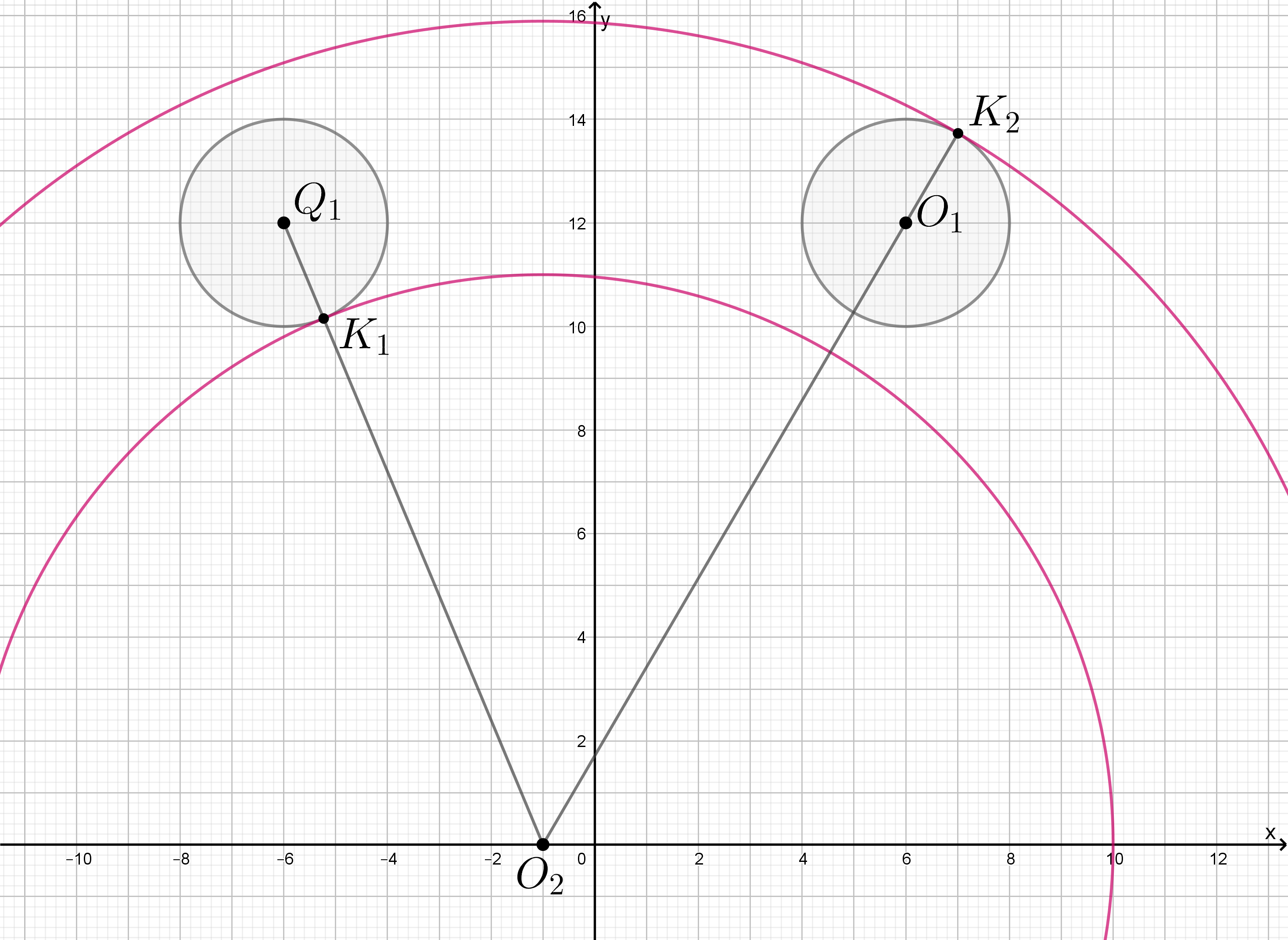
Если a – радиус окружности omega , то это значит, что a=MA (только правая) или a=MB (только левая).

Пусть А – точка касания окружности omega и окружности

Для точки А:

, MP = 5 (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),

В — точка касания окружности omega и окружности

Для точки В:

длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:

Есть еще точки С и D, в которых окружность omega касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:

, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.

Аналогично, для точки D:

и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.

Ответ: a=3 или

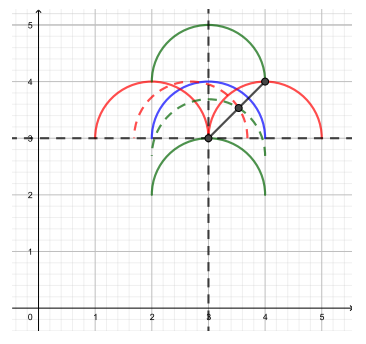
4. При каких значениях a система уравнений $left{ begin{array}{c}4left|y-3right|=12-3left|xright| \y^2-a^2=3left(2y-3right)-x^2 end{array}right.$ имеет 4 решения?

Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)

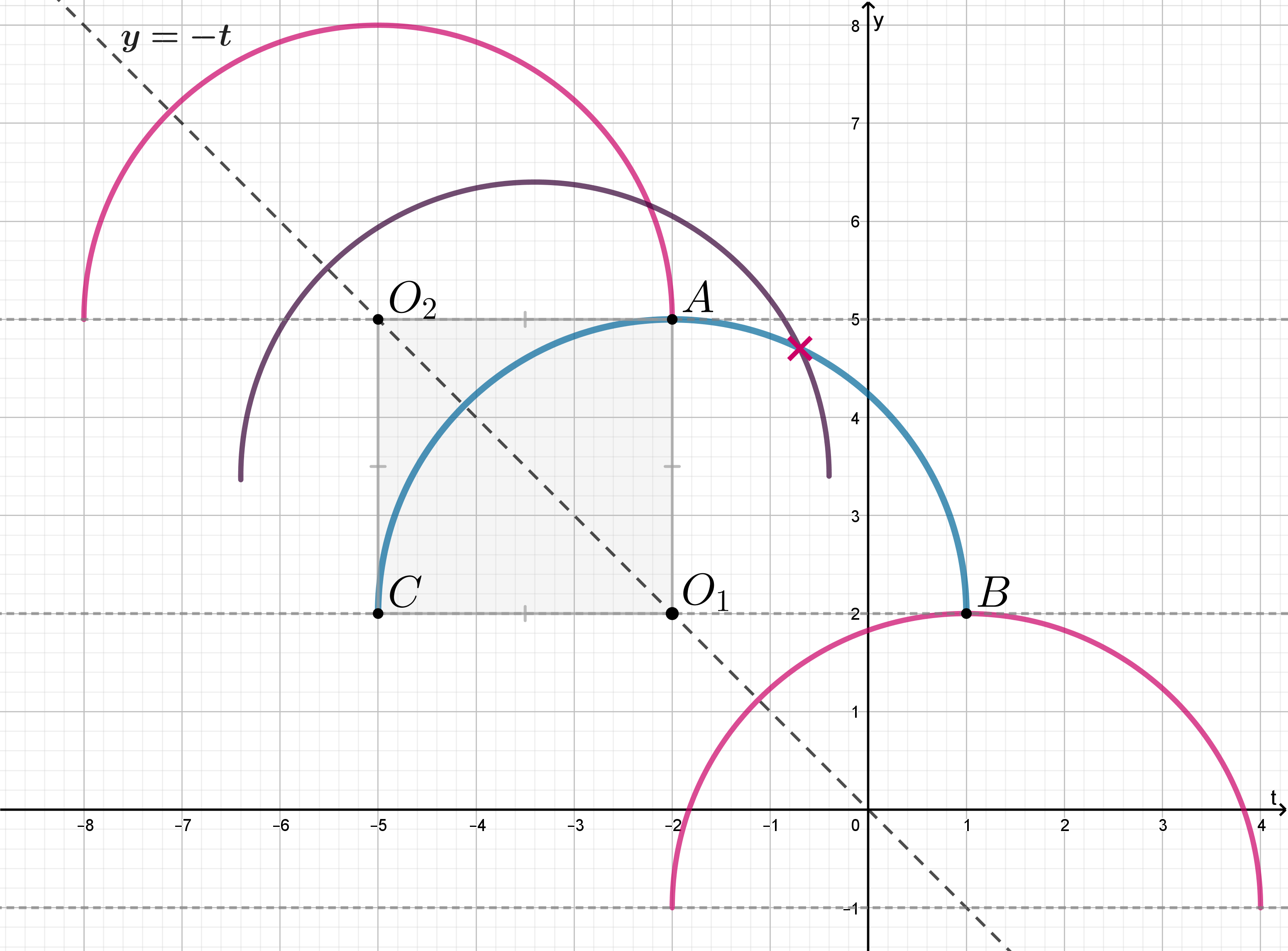
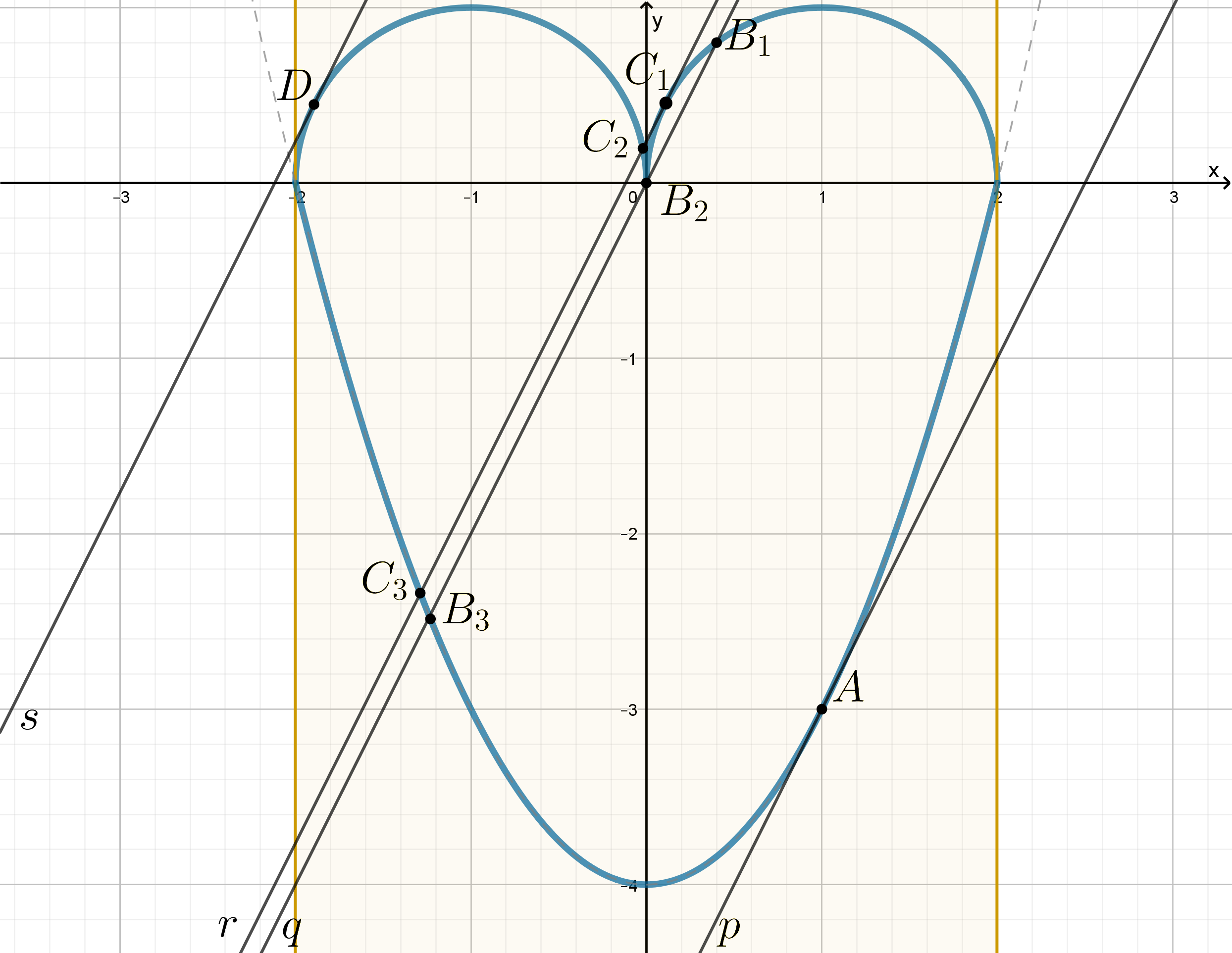
И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!

$left{ begin{array}{c}3left|xright|+4left|y-3right|=12 \x^2+y^2-6y+9=a^2 end{array}right.Longleftrightarrow left{ begin{array}{c}3left|xright|+4left|y-3right|=12 \x^2+{left(y-3right)}^2=a^2 end{array}right.$

Просто выделили полный квадрат во втором уравнении.

Сделаем замену y-3=t. Система примет вид:

$left{ begin{array}{c}3left|xright|+4left|tright|=12 \x^2+t^2=a^2 end{array}right.$

Вот теперь все видно! Рисовать будем в координатах (x; t).

Графиком первого уравнения является ромб, проходящий через точки с координатами и

Графиком второго уравнения является окружность с радиусом и центром в начале координат.

Когда же система имеет ровно 4 решения?

1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.

Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.

Диагонали нашего ромба равны 8 и 6. Значит,

Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

При этом h=2R. Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда $R=frac{12}{5} = left|aright|.$

Мы получили ответ:

$a=pm frac{12}{5}$

2) Есть второй случай, и мы его найдем.

Давайте посмотрим — если уменьшить радиус окружности, сделав $R textless frac{12}{5}$ , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.

Пусть радиус окружности больше, чем $frac{12}{5}$ , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.

Пусть радиус окружности равен 3. Тогда система имеет 6 решений.

А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!

Значит, Объединим случаи и запишем ответ:

Ответ: $left[ begin{array}{c}left|aright|=frac{12}{5} \3 textless left|aright| textless 4 end{array}right.$

Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Графический метод решения задач с параметрами» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Радиус — это важнейший элемент окружности

Что такое радиус

Радиус и диаметр

Свойства радиуса

Длина и площадь окружности через радиус

Длина окружности

Площадь окружности

Вместо заключения

Комментарии и отзывы (2)

Как найти радиус окружности

Основные понятия

Формула радиуса окружности

Если известна площадь круга

Если известна длина

Если известен диаметр окружности

Если известна диагональ вписанного прямоугольника

Если известна сторона описанного квадрата

Если известны стороны и площадь вписанного треугольника

Если известна площадь и полупериметр описанного треугольника

Если известна площадь сектора и его центральный угол

Если известна сторона вписанного правильного многоугольника

Скачать онлайн таблицу

Нахождение радиуса круга: формула и примеры

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

2. Через площадь круга

Примеры задач

Задания с параметрами, окружности

Вам также может понравиться

Как найти то что нужно в поисковике

Как найти номер числа арифметической прогрессии

Как составить аукционную заявку

Добавить комментарий Отменить ответ