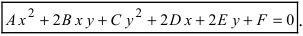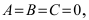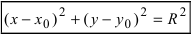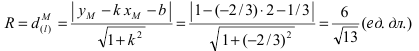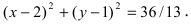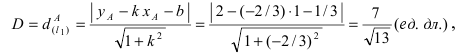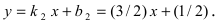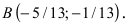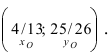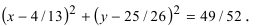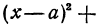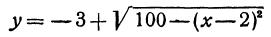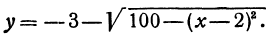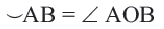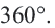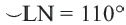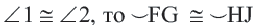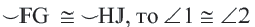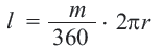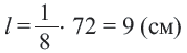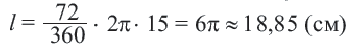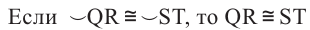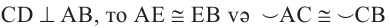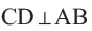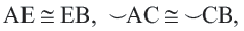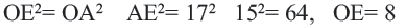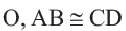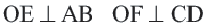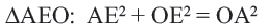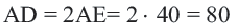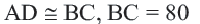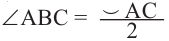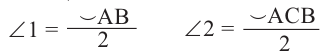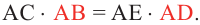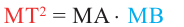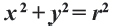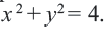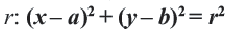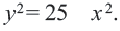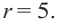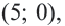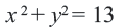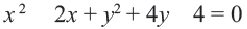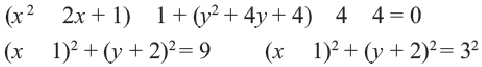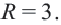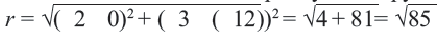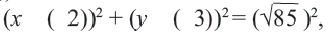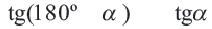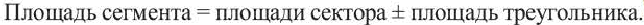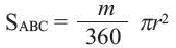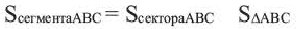Как найти радиус окружности по двум точкам

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Нахождение радиуса круга: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:

C = 2 π R

π – число, приближенное значение которого равно 3,14.

2. Через площадь круга

Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:

S = π R 2

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

[spoiler title=”источники:”]

[/spoiler]

Как найти радиус круга

2 методика:Вычисление радиуса по основным величинамВычисление радиуса по трем точкам на окружности

Радиус круга – отрезок, соединяющий центр круга с любой точкой на его окружности. Значение радиуса используется для вычисления длины окружности, площади круга, диаметра окружности, а также при нахождении объема трехмерных фигур, например, объема цилиндра. Радиус круга равен d/2, где d – диаметр круга; C/2π, где C – длина окружности; √(A/π), где A – площадь круга.

Шаги

Метод 1 из 2: Вычисление радиуса по основным величинам

Определение основных величин

1. 
   1
   Радиус можно найти по известным значениям основных величин круга/окружности. К таким величинам относятся:
   • Длина окружности (C).
   • Диаметр (D) (отрезок, соединяющей две точки на окружности и проходящий через центр круга).
   • Радиус (R) (отрезок, соединяющий центр круга с любой точкой на окружности).
   • Площадь (A) (пространство, ограниченное окружностью).
   • Число Пи (π) (математическая постоянная, представляющая отношение длины окружности к ее диаметру; это число применяется при вычислении всех основных величин круга и обычно округляется до 3,14).
2. 
   2
   Ниже приведены формулы для вычисления диаметра, длины окружности и площади круга; каждая из них включает радиус. Запомните: обособив радиус на одной стороне формулы, вы сможете найти его по известным значениям основных величин круга/окружности.
   • D = 2r. Диаметр вдвое больше радиуса.
   • С = πD = 2πr. Длина окружности равна произведению π на ее диаметр. Так как диаметр в два раза больше радиуса, то длина окружности равна произведению π на двойку и на радиус этой окружности.
   • A = πr^2. Площадь круга равна произведению квадрата его радиуса на π.

Вычисление радиуса по формулам

1. 
   1
   Если вам дан диаметр, разделите его пополам (на 2) и получите радиус. Так как D = 2r, то r =D/2.
   • Например, если диаметр круга равен 10 м, то радиус круга равен 10/2 = 5 м.
2. 
   2
   Если вам дана длина окружности, разделите ее на 2π и получите радиус. Так как C = 2πr, то r = C/2π.
   • Например, если длина окружности равна 10 см, то сначала разделите это значение на π: 10/π = 3,14 см. Теперь разделите полученное значение на 2, чтобы вычислить радиус: 3,14/2 = 1,59 см.
3. 
   3
   Если вам дана площадь круга, разделите ее на π и из полученного значения извлеките квадратный корень, чтобы найти радиус. Так как А = πr2, то r = √(A/π).
   • Например, площадь круга равна 10 м2. Сначала разделите это значение на π: 10/π = 3,14. Теперь из полученного значения извлеките квадратный корень, чтобы найти радиус: √3,14 = 1,78 м.

Метод 2 из 2: Вычисление радиуса по трем точкам на окружности

1. 
   1
   Если вам не даны значения диаметра, длины окружности или площади круга, вы можете вычислить радиус круга по координатам трех точек на окружности (назовем их P1, P2 и P3). Это делается при помощи одной из двух формул, приведенных ниже.
   • Формулы для нахождения радиуса круга по трем точкам, лежащем на окружности:
     • (abc)/(√(a + b + c)(b + c – a)(c + a – b)(a + b – c)), где a, b, c – стороны треугольника с вершинами в точках P1, P2, P3.[1]
     • a/(2sin(θ)), где a –сторона треугольника с вершинами в точках P1, P2, P3; θ – противолежащий угол.
   • Во второй формуле вам нужно знать только координаты двух точек и угол; если угол не дан, вам понадобятся координаты всех трех точек.
2. 
   2
   Найдите расстояние между каждыми двумя точками, чтобы определить значения сторон треугольника. Для этого подставьте известные вам координаты в формулу: Расстояние = √((x2 – x1)2 + (y2 – y1)2), где x1,y1 – координаты первой точки; x2,y2 – координаты второй точки.
   • Пример. На окружности круга лежат точки с координатами (3,0), (3,8) и (-1, 4). Найдите расстояние между точками (3,8) и (-1,4) по следующей формуле (то есть вы находите сторону треугольника):
     • √((x2 – x1)2 + (y2 – y1)2)
     • √((-1 – 3)2 + (4 – 8)2)
     • √((-4)2 + (-4)2)
     • √(16 + 16) = √(32) = 5,66
3. 
   3
   Найдите расстояние между двумя другими парами точек (то есть найдите две другие стороны треугольника) при помощи процесса, описанного в предыдущем шаге. Подставьте известные вам координаты в ту же формулу: Расстояние = √((x2 – x1)2 + (y2 – y1)2).
   • В нашем примере вам необходимо найти расстояние между точками (3,0) и (3,8) и между точками (3,0) и (-1, 4). В первой паре меняется только координата «у», поэтому расстояние равно 8. Расстояние между второй парой точек вычислите следующим образом:
     • √((x2 – x1)2 + (y2 – y1)2)
     • √((-1 – 3)2 + (4 – 0)2)
     • √((-4)2 + (4)2)
     • √(16 + 16) = √(32) = 5,66. Таким образом, стороны треугольника равны 5,66; 8; 5,66.
4. 
   4
   Воспользуйтесь формулой (abc)/(√(a + b + c)(b + c – a)(c + a – b)(a + b – c)) для вычисления радиуса круга (a, b, c – стороны треугольника). Для этого подставьте в эту формулу найденные вами стороны треугольника.
   • В нашем примере а = 5,66; b = 8; с = 5,66.
     • (abc)/(√(a + b + c)(b + c – a)(c + a – b)(a + b – c))
     • ((5,66)(8)(5,66))/(√(5,66 + 8 + 5,66)(8 + 5,66 – 5,66)(5,66 + 5,66 – 8)(5,66 + 8 – 5,66))
     • (256,28)/(√(19,32)(8)(3,32)(8))
     • (256,28)/(√(4105,11))
     • (256,28)/(64,07) = 4. Радиус нашего круга равен 4. Этот ответ верный, потому что сторона треугольника, равная 8, проходит через центр круга, то есть это его диаметр. Так как радиус равен половине диаметра, то 8/2 = 4.
5. 
   5
   Теперь найдем угол, противолежащий найденной стороне треугольника, по формуле (теорема косинусов): c2 = a2 + b2 – 2abCos(θ), где a, b, c – стороны треугольника, θ – угол между сторонами а и b, противолежащий стороне с. Найдя противолежащий угол, вы можете вычислить радиус по формуле: a/(2sin(θ))).
   • В нашем примере а = 5,66; b = 8; с = 5,66. Найдем угол, противолежащий первой стороне.
     • c2 = a2 + b2 – 2abCos(θ)
     • 5,662 = 5,662 + 82 – 2(5,66)(8)Cos(θ)
     • 32,04 = 32,04 + 64 – 90,56Cos(θ)
     • -64 = – 90,56Cos(θ)
     • 0.707 = Cos(θ)
     • θ = 45o (для нахождения угла необходимо вычислить arcos).
6. 
   6
   Подставьте известные вам значения стороны треугольника и противолежащего угла в формулу а/(2sin(θ)), чтобы найти радиус круга. Эта формула выведена из теоремы синусов, которая гласит, что отношение стороны треугольника к ее противолежащему углу равно удвоенному радиусу (или диаметру) окружности, описанной вокруг треугольника, то есть а/sin(θ) = 2r.[2]
   • В нашем примере сторона равна 5,66, а противолежащий угол равен 45o. Подставьте эти значения в формулу.
     • a/(2sin(θ))
     • 5,66/(2sin(45o))
     • 5,66/ 2(0,707)
     • 5,66/1,414 = 4. Обратите внимание, что вы получили такое же значение радиуса, как и при использовании формулы ((abc)/(√(a + b + c)(b + c – a)(c + a – b)(a + b – c))).

Советы

• Пользуйтесь калькулятором для проверки ответа.
• Для получения более точных результатов на калькуляторе используйте клавишу π.

Содержание:

Окружность:

Определение: Кривой второго порядка называется линия, описываемая уравнением

Замечание: Если коэффициенты

При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.

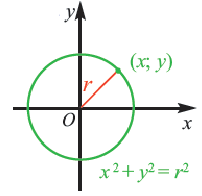
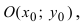
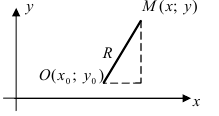
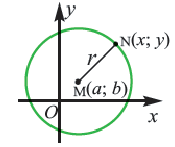
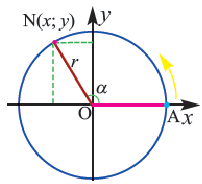
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки называемой центром окружности, на расстояние R, которое называется радиусом окружности.

Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:

Рис. 27. Вывод уравнения окружности.

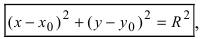
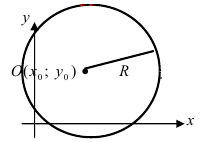
Из рисунка видно, что по теореме Пифагора которое определяет уравнение окружности (Рис. 28):

Рис. 28. Окружность.

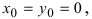
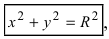
Если то уравнение принимает вид который называется каноническим уравнением окружности.

Пример:

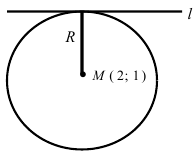
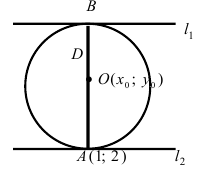
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 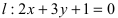является касательной к окружности.

Решение:

Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.

В уравнении окружности 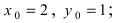таким образом оно имеет вид:

Пример:

Составить уравнение окружности, касающейся двух параллельных прямых 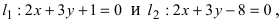причем одной из них в т. А (1; 2).

Решение:

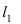
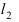
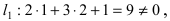
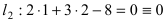
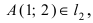
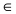
Прежде всего определим, на какой из прямых или лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых

следовательно, точка A(1; 2) принадлежит линии (в сокращенной форме это предложение пишут так: где значок означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой

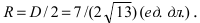
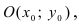
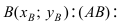
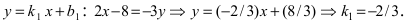
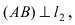
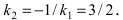
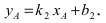
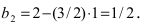
а радиус окружности Найдём координаты центра окружности точки которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом Так как прямаято её угловой коэффициент Прямая (АВ) проходит через известную точку A(1;2), следовательно, Отсюда находим Таким образом,уравнение прямой (АВ):

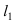
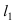
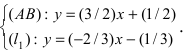
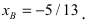
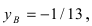
Найдем координаты точки B, которая является пересечением прямых и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых и (АВ): (В): Подставим выражение для переменной у из второго у равнения в первое, получим Подставив это значение во второе уравнение системы, найдем т.е.

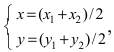
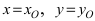
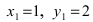
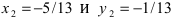
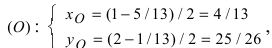
Для вычисления координат точки О применим формулы деления отрезка пополам (О): в этой формуле (координаты точки О), (координаты точки А), (координаты точки В), следовательно, т.е. координаты точки О

Таким образом, уравнение искомой окружности имеет вид:

Окружность в высшей математике

Рассмотрим уравнение

которое получается из уравнения (I), если положить , .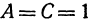

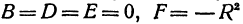
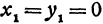
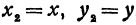
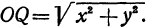
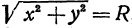
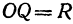
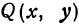
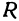
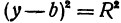
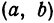
Если в формулу, выражающую расстояние между двумя точками, подставить , , то получим Из уравнения (1) находим, что , т. е. . Это значит, что все точки , координаты которых удовлетворяют уравнению (1), находятся на расстоянии от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса с центром в начале координат. Аналогично получаем, что уравнение определяет окружность радиуса с центром в точке .

Пример:

Найдем уравнение окружности с центром в точке и радиусом, равным 10.

Решение:

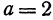
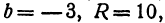
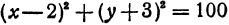
Полагая, получим .

Разрешим это уравнение относительно 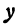, будем иметь

и

Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.

Центральный угол. Градусная мера дуги

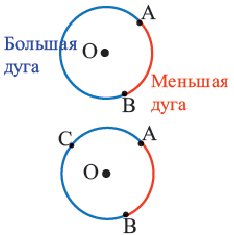
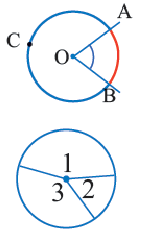
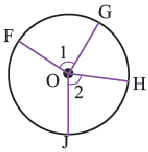
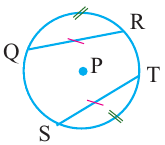
Дуга окружности. Если отметить на окружности точки и , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка является какой-либо точкой дуги , то . Если точки и являются концами диаметра, го каждая дуга является полуокружностью.

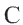
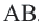
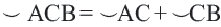
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла:

Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна

Дуги окружности и их величины

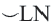
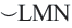
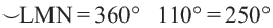
Пример: минорная дуга:

мажорная дуга:

Конгруэнтные дуги

В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.

Если

Если

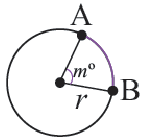
Длина дуги

Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.

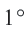
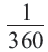
Длина дуги в равна части длины окружности.

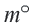
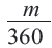
Длина дуги, соответствующей центральному углу с градусной мерой , составляет части длины окружности:

Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)

Пример №1

Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу .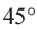

Решение:

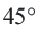
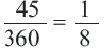
Так как центральный угол составляет часть полного угла, то длина искомой дуги:

Пример №2

Найдите длину дуги, соответствующей центральному углу 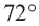в окружности радиусом 15 см.

Решение: подставляя значения 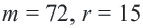в формулу длины дуги находим:

Окружность и хорда

Теорема о конгруэнтных хордах

Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.

Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.

1)Если 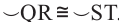, то

2)Если

Доказательство теоремы 1:

Теорема о серединном перпендикуляре хорд

Теорема 2.

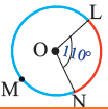
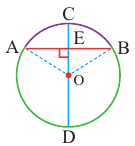
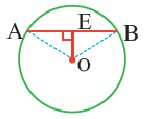
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.

Если

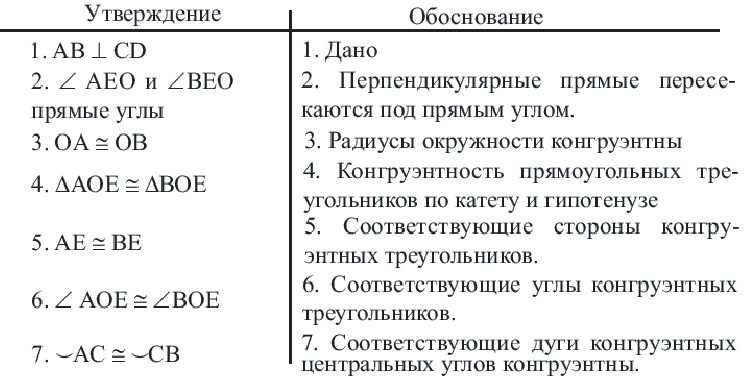
Доказательство теоремы 2.

Дано: – центральный угол,

Докажите:

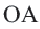
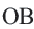
Начертите радиусы и окружности.

Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.

Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.

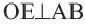
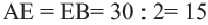
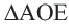
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если , то . Из по теореме Пифагора имеем:

Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности

Теорема 3.

Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.

Если 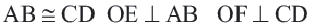, то

Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.

Доказательство теоремы 3

Дано: Окружность с центром

Докажите:

Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. и – серединные перпендикуляры конгруэнтных хорд и . , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности и : . Прямоугольные треугольники, и конгруэнтны (по катету и гипотенузе). Так как и являются соответствующими сторонами данных треугольников, то они конгруэнтны: . Теорема доказана.

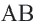
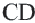
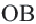
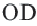
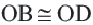
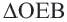
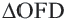
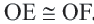
Задача. Хорды и находятся на одинаковом расстоянии от центра окружности. . Если радиус окружности равен 41 единице, то найдите .

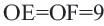
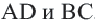
Решение: Так как хорды и находятся на одинаковом расстоянии от центра, то они конгруэнтны: Соединим точки и с точкой В прямоугольном треугольнике ; ; ;

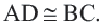
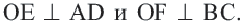
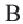
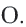
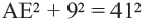
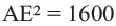
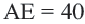
Так как

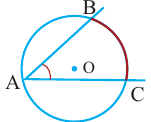
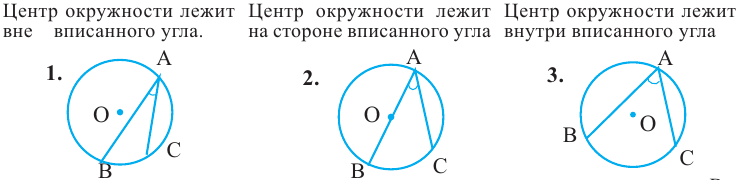
Угол, вписанный в окружность

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.

является углом вписанным в окружность с центром , а дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.

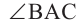
Угол, вписанный в окружность:

Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается.

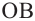
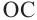
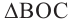
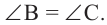
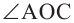
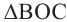
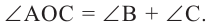
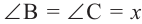
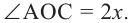
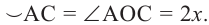
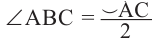
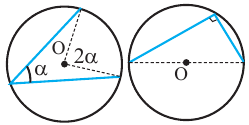
Доказательство (текстовое): и радиусы окружности и равнобедренный треугольник. Значит, Так как является внешним углом , Если примем, что , то Так как градусные меры центрального угла и опирающейся на него дуги равны, то Следовательно, .

Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.

Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.

Конгруэнтные углы, вписанные в окружность

Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. , .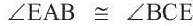

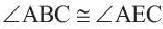
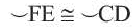
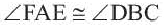
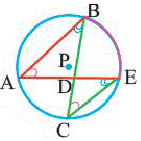
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если , то .

Касательная к окружности

Касательная. Признак касательной

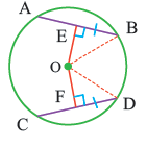
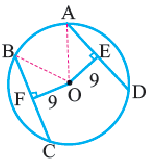
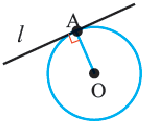
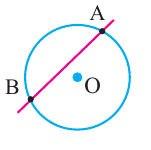
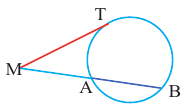
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

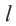
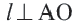
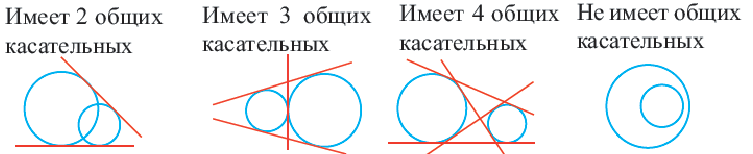
Прямая является касательной к окружности. Значит, Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.

Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.

Доказательство теоремы 1. Если прямая – касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая не перпендикулярна радиусу Проведем и на прямой выделим отрезок Тогда так как Значит, точка также находится на окружности. То есть прямая имеет с окружностью две общие точки, что противоречит условию. Значит,

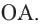
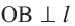
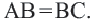
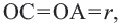
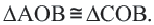
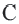
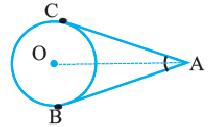
Свойства касательных, проведенных к окружности из одной точки

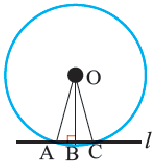
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.

и касательные, проведенные из точки к окружности с центром

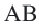
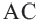
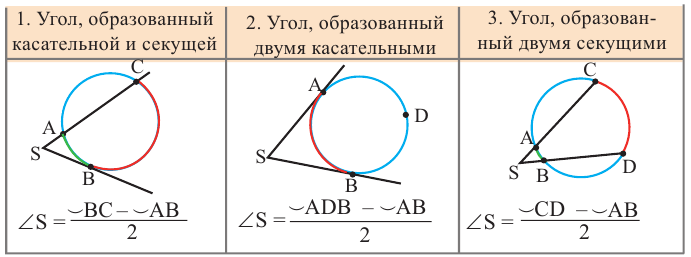
Углы, образованные секущими и касательными

Прямая, имеющая две общие точки с окружностью, называется секущей окружности.

Углы между двумя секущими

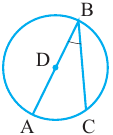
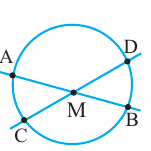
Вершина угла находится внутри окружности

Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному.

Углы между касательной и секущей

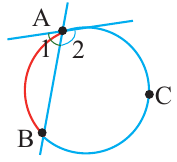
Вершина угла находится на окружности

Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.

Углы, образованные касательной и секущей

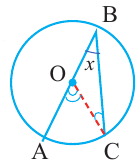
Вершина угла находится вне окружности

Теорема 1.

Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.

Отрезки секущих и касательных

Длина отрезков, секущих окружность

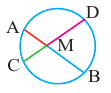
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.

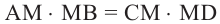
Теорема 2. Если из точки провести две прямые, пересекающие окружность соответственно в точках и , и то верно равенство

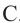
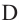
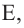
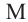
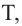
Теорема 3. Если из точки проведены прямая, которая пересекает окружность в точках и и касательная к окружности в точке то верно равенство:

Уравнение окружности

Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом и с центром в начале координат. Расстояние между центром окружности и ее любой точкой равно радиусу окружности.

Расстояние между двумя точками

Упрощение

Возведение обеих частей в квадрат

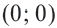
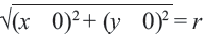
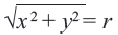
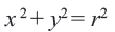
Уравнение окружности с центром в начале координат и радиусом :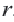

Например, уравнение окружности с центром в начале координат 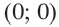и радиусом 2 имеет вид:

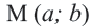
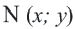
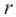
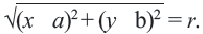
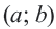
По формуле расстояния между центром окружности и точки на окружности радиуса имеем Возведя в квадрат обе части, получаем уравнение окружности с центром в точке и радиусом

Например, уравнение окружности с центром в точке 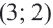и радиусом 4 имеет вид:

Пример №3

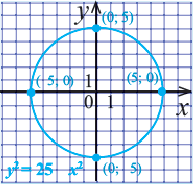
Постройте на координатной плоскости окружность, заданную уравнением

Решение: Напишем уравнение в виде 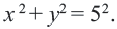Как видно,

Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 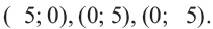Проведем окружность через эти точки.

Пример №4

Точка 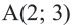находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.

Решение: Записав координаты точки в уравнении , получим: Уравнение этой окружности:

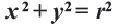
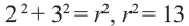
Пример №5

Найдем центр и радиус окружности, заданной уравнением

Решение:

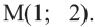
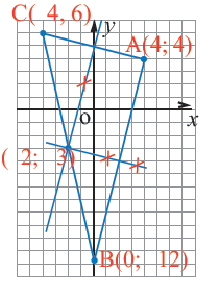
Центр окружности точка Радиус

Пример №6

Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 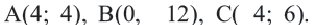На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.

Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 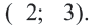Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,

Уравнение окружности:

Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.

Координаты точек, находящихся на окружности, и тригонометрические отношения

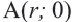
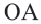
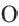
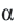
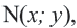
Если точка при повороте радиуса вокруг точки против движения часовой стрелки на угол преобразуется в точку то

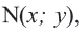
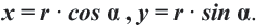
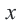
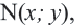
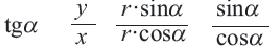
Для координат точки соответствующей углу поворота на окружности, верны формулы В этих формулах – угол, отсчитываемый от положительной оси против движения часовой стрелки. Если точка не находится на оси ординат, то .

Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 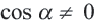почленным делением получаем:

С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.

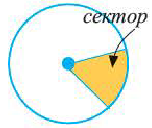
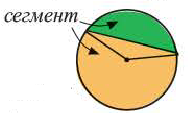
Сектор и сегмент

Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.

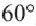
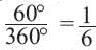
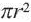
Например, часть круга, соответствующая центральному углу , составляет часть всего круга. Так как площадь круга , то площадь этого сектора будет Сегмент часть круга, ограниченная хордой и соответствующей дугой.

Площадь сектора

Площадь сектора:

Площадь сегмента:

Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь