Равносторонний треугольник на клетчатой бумаге
На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус вписанной в него окружности.
Поскольку формула радиуса вписанной в правильный треугольник окружности содержит иррациональность:
использовать её на экзамене, где требуется точный ответ, а не его приближённое значение, нет смысла. Да и длина стороны треугольника задана в таких заданиях не целым числом.
Зато высота треугольника — целое число. По свойству равностороннего треугольника его высота равна сумме радиусов вписанной и описанной окружности:
Итак, чтобы найти радиус вписанной в равносторонний треугольник окружности, нужно посчитать по клеткам длину высоты и найти от неё треть.
В данной задаче длина высоты равна 9 клеткам (h=9), следовательно,
На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус описанной около него окружности.
Находим по клеткам высоту данного треугольника:
Радиус описанной около равностороннего треугольника окружности составляет две третьих его высоты:
Как найти радиус окружности по клеточкам
На клетчатой бумаге с размером клетки 1 × 1 изображён вписанный в окружность угол ABC. Найдите его градусную величину.
Аналоги к заданию № 27890: 26237 27891 509571 Все
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого см. Поэтому
см 2 .
Хотелось бы более “научного” доказательства. Аргумент “это видно” не достаточен, так как всем видно разное. Спасибо!
На рисунке ВИДНО, что они равны. Или задайте прямые уравнениями и и найдите угол между ними. Но то, что уравнения именно такие, тоже ВИДНО по рисунку. Задания на работу с рисунками предполагают считывание информации с рисунка.
На клетчатой бумаге с размером клетки 1 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.
Треугольник прямоугольный, значит, радиус описанной вокруг него окружности равен половине гипотенузы.
На клетчатой бумаге нарисованы два круга
Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):
Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
Разделим результат на число Пи и запишем ответ.
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.
Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см 2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см 2 .
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.
Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
Выразим площадь большего круга, так как его радиус равен 6х:
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см 2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см 2 .
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.
Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3 ∙ х, то
Выразим площадь большего круга. Так как его радиус равен 4 ∙ х, то
Разделим площадь большего на площадь меньшего:
То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см 2 .
Вычислим радиус меньшего круга. Его площадь равна 9, значит,
Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:
Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:
Определяем площадь большего круга:
Находим разность: 16 – 9 = 7 см 2
На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.
В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?
По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.
Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
С уважением, автор проекта Александр Крутицких.
[spoiler title=”источники:”]
http://ege.sdamgia.ru/test?theme=123
http://matematikalegko.ru/plocshadi-figur/krug-chasti-kruga-na-liste-v-kletku.html
[/spoiler]
![]()
Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):

Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
![]()
Значит,
![]()
Разделим результат на число Пи и запишем ответ.
Ответ: 3

На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.

Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
![]()
Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:
![]()
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см2.
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
![]()
Выразим площадь большего круга, так как его радиус равен 6х:
![]()
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см2.
Ответ: 3

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3∙х, то
![]()
Выразим площадь большего круга. Так как его радиус равен 4∙х, то
![]()
Разделим площадь большего на площадь меньшего:

То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
![]()
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см2.
*Второй способ.
Вычислим радиус меньшего круга. Его площадь равна 9, значит,

Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:

Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:

Определяем площадь большего круга:

Находим разность: 16 – 9 = 7 см2
Ответ: 7

На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.

В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
Ответ: 24

На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?

По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.
Ответ: 96
![]()
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Посмотреть решение
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.

Посмотреть решение
Небольшой итог.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
С уважением, автор проекта Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Задача 1
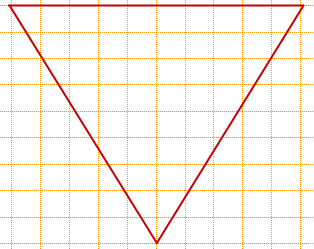 На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус вписанной в него окружности.
На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус вписанной в него окружности.
Решение:
Поскольку формула радиуса вписанной в правильный треугольник окружности содержит иррациональность:
![]()
использовать её на экзамене, где требуется точный ответ, а не его приближённое значение, нет смысла. Да и длина стороны треугольника задана в таких заданиях не целым числом.
Зато высота треугольника — целое число. По свойству равностороннего треугольника его высота равна сумме радиусов вписанной и описанной окружности:
![]()
причем
![]()
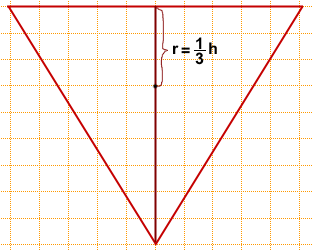 Итак, чтобы найти радиус вписанной в равносторонний треугольник окружности, нужно посчитать по клеткам длину высоты и найти от неё треть.
Итак, чтобы найти радиус вписанной в равносторонний треугольник окружности, нужно посчитать по клеткам длину высоты и найти от неё треть.
В данной задаче длина высоты равна 9 клеткам (h=9), следовательно,
![]()
Ответ: 3.
Задача 2
На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус описанной около него окружности.
Решение:
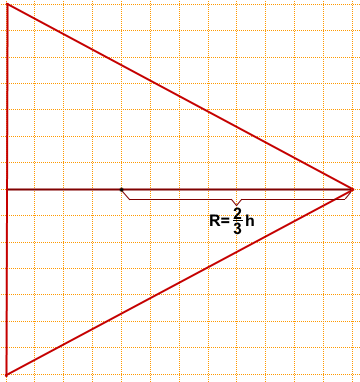 Находим по клеткам высоту данного треугольника:
Находим по клеткам высоту данного треугольника:
h=12.
Радиус описанной около равностороннего треугольника окружности составляет две третьих его высоты:
![]()
![]()
Ответ: 8.
Задача № 1
На клетчатой бумаге с размером клетки 1 на 1 изображён прямоугольник (Рис. 1). Найдите радиус окружности, описанной около этого прямоугольника.
Решение
Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, описанной около прямоугольника, равен половине его диагонали».
Найдем диагональ этого прямоугольника.
Из рисунка (Рис. 1) видно, что BD = 5
Диагональ равна 5, поэтому радиус равен 2,5.
Ответ: 2,5.
Задача № 2
На клетчатой бумаге с размером клетки √2 на √2 изображён квадрат (Рис. 2). Найдите радиус окружности, вписанной в этот квадрат.

Решение
Учтем, что по условию задачи размер клеток равен √2 на √2. Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, вписанной в квадрат, равен половине его стороны». Найдем сторону квадрата:

Тогда радиус вписанной окружности равен:

Ответ: 2.
Задача № 3
На клетчатой бумаге с размером клетки 1 на 1 изображён равносторонний треугольник (Рис. 3). Найдите радиус описанной около него окружности.

Решение
Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, описанной вокруг равностороннего треугольника, равен двум третьим его высоты». Из рисунка (Рис. 3) видим, что высота равна «3». Поэтому радиус описанной окружности будет равен 3 х 2/3 = 2.
Ответ: 2.
Автор – Андрей Найденов
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Помогите найти радиус окружности
ananastyaryder
Знаток
(343),
на голосовании
7 лет назад
Сидели мы на уроке алгебры и разбирали графики. Нам попалась окружность с неизвестным радиусом. Вот у нас учитель и спросил, как найти радиус (диаметр) такой окружности. Мы что только не предлагали: считать по клеточкам, составить уравнение, описать треугольник и с помощью теоремы синусов найти радиус. Все не так
Подскажите, пожалуйста:)
Голосование за лучший ответ
Валерий Малый
Профи
(721)
7 лет назад
1. напечатать в реальном размере и измерить
2. Взять циркуль, отметить границы на листе бумаги и измерить
Андрей Тялин
Оракул
(68720)
7 лет назад
По графику видно, что радиус равен примерно 2,5 (ед.).
С довольно высокой точностью.
λ
Искусственный Интеллект
(193205)
7 лет назад
пальцем легко считается, диаметр 5
значит радиус 2,5
