Как найти радиус окружности по клеточкам - Сайт, где вы сможете решить свои вопросы

Помогите найти радиус окружности

ananastyaryder

Знаток

(343),
на голосовании

7 лет назад

Сидели мы на уроке алгебры и разбирали графики. Нам попалась окружность с неизвестным радиусом. Вот у нас учитель и спросил, как найти радиус (диаметр) такой окружности. Мы что только не предлагали: считать по клеточкам, составить уравнение, описать треугольник и с помощью теоремы синусов найти радиус. Все не так
Подскажите, пожалуйста:)

Голосование за лучший ответ

Валерий Малый

Профи

(722)

7 лет назад

1. напечатать в реальном размере и измерить
2. Взять циркуль, отметить границы на листе бумаги и измерить

Андрей Тялин

Оракул

(68740)

7 лет назад

По графику видно, что радиус равен примерно 2,5 (ед.).
С довольно высокой точностью.

λ

Искусственный Интеллект

(193625)

7 лет назад

пальцем легко считается, диаметр 5
значит радиус 2,5

Источник

Задачи на клетчатой бумаге интересны тем, что можно их решать различными способами – и через дополнительное построение, и через различные геометрические формулы. Так как задач таких сейчас полно в сети, ещё раз обозначу себе картинкой условие:

У нас нет ничего в условии кроме длины клетки, равной 1/√π

Как найти площадь?

Например, по такой формуле, где альфа – размер угла.

Но у нас нет ни угла, ни радиуса.

Значит, находим радиус. На глаз тут 4,5 клетки, но мы будем точнее, если нарисуем вот такой треугольник прямоугольник, в котором радиус будет гипотенузой и через теорему Пифагора его найдём.

(4/√π)2 + (2/√π)2 = 16/π+4/π = √(20/π)

Как найти угол? Если разделить всю окружность на 4 части, то видно, что закрашенная часть составит целую четверть и ещё её половинку. То бишь, 1/4+0,5Х1/4 Это не что иное как 3/8

Теперь считаем угол: 360Х3/8=135 градусов.

Теперь, когда у нас есть все данные, подставляем в формулу.

S=135/360 Х π Х (√(20/π))2

Квадрат и корень квадратный сокращаются, получаем 135/360 Х π Х 20/π

Следом сокращается и п, остаётся 135/360 Х 20/1 = 135/18 = 7,5

Поскольку площадь измеряется в квадратных сантиметрах в нашей задаче, то и ответ будет 7,5 кв.см

Источник

Задача № 1

На клетчатой бумаге с размером клетки 1 на 1 изображён прямоугольник (Рис. 1). Найдите радиус окружности, описанной около этого прямоугольника.

Решение

Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, описанной около прямоугольника, равен половине его диагонали».

Найдем диагональ этого прямоугольника.

Из рисунка (Рис. 1) видно, что BD = 5

Диагональ равна 5, поэтому радиус равен 2,5.

Ответ: 2,5.

Задача № 2

На клетчатой бумаге с размером клетки √2 на √2 изображён квадрат (Рис. 2). Найдите радиус окружности, вписанной в этот квадрат.

Решение

Учтем, что по условию задачи размер клеток равен √2 на √2. Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, вписанной в квадрат, равен половине его стороны». Найдем сторону квадрата:

Тогда радиус вписанной окружности равен:

Ответ: 2.

Задача № 3

На клетчатой бумаге с размером клетки 1 на 1 изображён равносторонний треугольник (Рис. 3). Найдите радиус описанной около него окружности.

Решение

Чтобы найти радиус окружности, необходимо вспомнить правило, гласящее: «Радиус окружности, описанной вокруг равностороннего треугольника, равен двум третьим его высоты». Из рисунка (Рис. 3) видим, что высота равна «3». Поэтому радиус описанной окружности будет равен 3 х 2/3 = 2.

Ответ: 2.

Автор – Андрей Найденов

Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

Задача 1

На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус вписанной в него окружности.

Решение:

Поскольку формула радиуса вписанной в правильный треугольник окружности содержит иррациональность:

$[r = frac{a}{{2sqrt 3 }} = frac{{asqrt 3 }}{6},]$

использовать её на экзамене, где требуется точный ответ, а не его приближённое значение, нет смысла. Да и длина стороны треугольника задана в таких заданиях не целым числом.

Зато высота треугольника — целое число. По свойству равностороннего треугольника его высота равна сумме радиусов вписанной и описанной окружности:

причем

$[r = frac{1}{3}h,R = frac{2}{3}h.]$

Итак, чтобы найти радиус вписанной в равносторонний треугольник окружности, нужно посчитать по клеткам длину высоты и найти от неё треть.

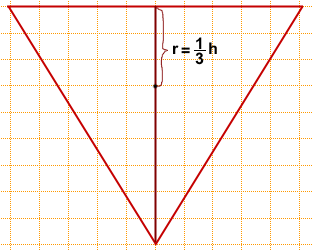
В данной задаче длина высоты равна 9 клеткам (h=9), следовательно,

$[r = frac{1}{3}h = frac{1}{3} cdot 9 = 3.]$

Ответ: 3.

Задача 2

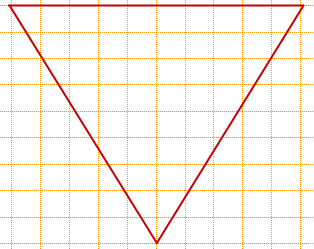
На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус описанной около него окружности.

Решение:

Находим по клеткам высоту данного треугольника:

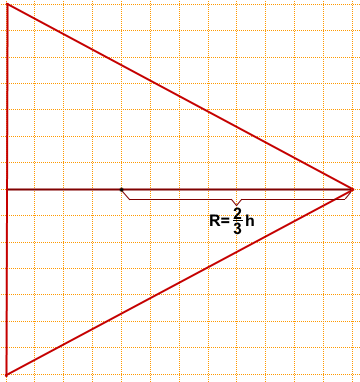
h=12.

Радиус описанной около равностороннего треугольника окружности составляет две третьих его высоты:

$[ R = frac{2}{3}h = frac{2}{3} cdot 12 ]$

Ответ: 8.

Источник

3 октября 2013

В этом уроке мы разберем еще одну задачу B5 на площади секторов из ЕГЭ по математике, однако будьте очень внимательны: на первый взгляд все считается очень просто. Но в самом конце решения многие ученики допускают очень обидную ошибку. Сейчас вы поймете, о чем идет речь. Итак, задача:

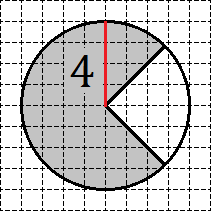
Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как решать такую задачу? В первую очередь, поскольку речь идет о площади сектора, нам нужно знать формулу площади круга:

S = πR²

где R — радиус круга. Следовательно, для решения нам потребуется найти этот самый радиус. В данной задаче все очень просто: проводим вертикальный радиус и считаем клеточки.

Отсюда сразу получаем, что радиус R = 4. Таким образом, площадь круга S равна:

S = π · 4² = 16π

Обратите внимание: нам очень повезло с радиусом. Потому что в настоящих задачах далеко не всегда верхняя точка окружности лежит в узлах координатной сетки. Однако где-то на окружности обязательно найдется точка с целочисленными координатами, которая точно будет лежать в узле сетки. Вот ее и надо использовать для вычисления радиуса. Давайте посмотрим, каким образом.

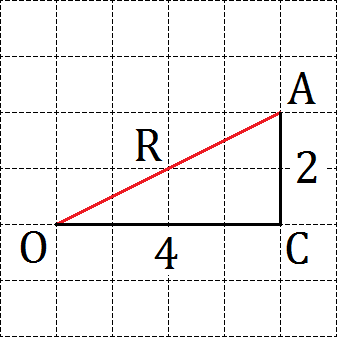
Для этого нам потребуется отдельная сетка. Отметим на ней центр окружности (точку O) и некую гипотетическую точку A, которая должна лежать на нашей окружности. Допустим, это будет выглядеть следующим образом:

Тогда отрезок OA будет радиусом этой окружности. Как его найти? Достроим до прямоугольного треугольника наш отрезок. Если двигаться вдоль линий координатной сетки, мы получим прямоугольный треугольник OAC с прямым углом C. Разумеется, полученная таким образом точка C не будет лежать на окружности — она лежит где-то внутри. Но этого нам и не требуется. Главное, что мы легко можем найти катеты: OC = 4, AC = 2.

Тогда мы можем найти радиус R (он же — отрезок OA) по теореме Пифагора:

R² = 4² + 2² = 16 + 4 = 20

И тогда получилось бы, что вместо 16π площадь всего круга равнялась бы 20π. В остальном решение было бы полностью аналогичным, поэтому возвращаемся к нашей исходной задаче. Мы только что нашли площадь круга, а нам надо найти площадь сектора. Давайте схематично перерисуем круг и разделим его на 8 равных частей, как пиццу (стандартная практика в задачах B5). Затем закрашиваем на получившемся рисунке те сектора, которые на исходном чертеже также были закрашены:

Получаем, что закрашенных кусочков было k = 6, а всего их изначально n = 8. Поскольку все части равные, мы можем найти площадь каждого маленького сектора, разделив общую площадь круга на 8:

S_sec = 16π/8 = 2π

А поскольку в закрашенном секторе таких кусочков k = 6, то искомая площадь будет равна

S = 6 · S_sec = 6 · 2π = 12π

Но в задаче B5 от нас требуется найти не просто площадь сектора, а величину S/π. Поэтому выполняем последний шаг. Подставляем и получаем:

12π : π = 12

Это и есть ответ. Так в чем же главная ошибка учеников, которые решают подобные задачи? Дело в том, что многие начинают считать площадь меньшего из секторов, изображенных на рисунке. Однако этот сектор не закрашен. В результате при правильных по существу расчетах многие ученики получают неправильный ответ. Согласитесь, обидная ошибка?

Поэтому рекомендация следующая: внимательно читайте условие задачи B5! Если требуется найти площадь закрашенного сектора, то именно закрашенный сектор и нужно искать. Даже если на чертеже он занимает большую часть круга. А если требуется найти площадь незакрашенного сектора, то об этом обязательно будет указано в условии. Поэтому прежде чем записывать ответ, еще раз проверьте, что от вас требуется: закрашенный сектор или незакрашенный? И тогда дополнительный балл на ЕГЭ по математике вам гарантирован.:)

Смотрите также: