Уравнение окружности по трем точкам
Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.
Уравнение окружности
r 2 = (x — h) 2 + (y — k) 2
- h,k — координаты центра Окружности
- x,y — координаты точки окружности
- r — радиус
Пример
Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)
Решение :
Подставляем координаты точек в формулу
- (2 — h) 2 + (2 — k) 2 = r 2
- (2 — h) 2 + (4 — k) 2 = r 2
- (5 — h) 2 + (5 — k) 2 = r 2
Шаг :2
Найдем значение k упрощая 1 и 2 уравнения
- (2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
- 4 — 4h + h 2 + 4 — 4k + k 2 = 4 — 4h + h 2 +16 — 8k + k 2
- 8 — 4k = 20 — 8k
- k= 3
Шаг :3
Найдем значение h упрощая уравнения 2 и 3
- (2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
- 4 — 4h + h 2 + 4 — 4k + k 2 = 25 — 10h + h 2 + 25 — 10k + k 2
- 8 — 4k — 4h = 50 — 10h — 10k
- 6k + 6h = 42
Подставив значение k=3 в уравнение
Получаем координаты точки центра (h,k) = ( 4,3 )
Шаг :4
Подставим значения h,k в формулу
- r 2 = (x — h) 2 + (y — k) 2
- r 2 = (2 — 4) 2 + (2 — 3) 2
- r 2 = (-2) 2 + (-1) 2
- r 2 = 5
- r = 2.24
Шаг :5
Подставим значения h, k в уравнение окружности
(x — h) 2 + (y — k) 2
Уравнение окружности = (x — 4) 2 + (y — 3) 2
Уравнение окружности, проходящей через три заданные точки
Этот онлайн калькулятор выводит уравнение окружности, проходящей через три заданные точки
Этот онлайн-калькулятор находит окружность, проходящую через три заданные точки. Калькулятор находит центр, радиус и уравнение окружности, и строит окружность на графике. Методы, использованные для нахождения центра и радиуса окружности, описаны ниже под калькулятором.
Уравнение окружности, проходящей через три заданные точки
Первая точка
Вторая точка
Третья точка
Центр
Как найти окружность, проходящюю через три заданные точки
Давайте вспомним как выглядит уравнение окружности в стандартной форме:
Так как все три точки принадлежат одной окружности, мы можем записать систему уравнений
Значения , и мы знаем. Давайте сделаем подстановку с неизвестными переменнами a, b и c.
Теперь у нас есть три линейных уравнения для трех неизвестных – составим систему уравнений соответствующую матричной форме:
Мы можем решить эту систему уравнений, используя, к примеру, Гауссово исключение. (подробнее прочитать об этом можно здесь – Решение системы линейных алгебраических уравнений методом Гаусса ). “Нет решений” – означает, что точки коллинеарны и окружность через них провести нельзя.
Координаты центра окружность и ее радиус относится к подобному решению
Зная центр и радиус, мы можем получить уравнение окружности, используя этот калькулятор – Уравнение окружности по заданному центру и радиусу в различных формах
Окружность и радиус окружности по трем точкам
Уравнение окружности, проходящей через три заданные точки
Этот онлайн калькулятор выводит уравнение окружности, проходящей через три заданные точки
Этот онлайн-калькулятор находит окружность, проходящую через три заданные точки. Калькулятор находит центр, радиус и уравнение окружности, и строит окружность на графике. Методы, использованные для нахождения центра и радиуса окружности, описаны ниже под калькулятором.
Уравнение окружности, проходящей через три заданные точки
Первая точка
Вторая точка
Третья точка
Центр
Как найти окружность, проходящюю через три заданные точки
Давайте вспомним как выглядит уравнение окружности в стандартной форме:
Так как все три точки принадлежат одной окружности, мы можем записать систему уравнений
Значения , и мы знаем. Давайте сделаем подстановку с неизвестными переменнами a, b и c.
Теперь у нас есть три линейных уравнения для трех неизвестных — составим систему уравнений соответствующую матричной форме:
Мы можем решить эту систему уравнений, используя, к примеру, Гауссово исключение. (подробнее прочитать об этом можно здесь — Решение системы линейных алгебраических уравнений методом Гаусса ). «Нет решений» — означает, что точки коллинеарны и окружность через них провести нельзя.
Координаты центра окружность и ее радиус относится к подобному решению
Зная центр и радиус, мы можем получить уравнение окружности, используя этот калькулятор — Уравнение окружности по заданному центру и радиусу в различных формах
Уравнение окружности по трем точкам
Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.
Уравнение окружности
r 2 = (x — h) 2 + (y — k) 2
- h,k — координаты центра Окружности
- x,y — координаты точки окружности
- r — радиус
Пример
Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)
Решение :
Подставляем координаты точек в формулу
- (2 — h) 2 + (2 — k) 2 = r 2
- (2 — h) 2 + (4 — k) 2 = r 2
- (5 — h) 2 + (5 — k) 2 = r 2
Шаг :2
Найдем значение k упрощая 1 и 2 уравнения
- (2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
- 4 — 4h + h 2 + 4 — 4k + k 2 = 4 — 4h + h 2 +16 — 8k + k 2
- 8 — 4k = 20 — 8k
- k= 3
Шаг :3
Найдем значение h упрощая уравнения 2 и 3
- (2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
- 4 — 4h + h 2 + 4 — 4k + k 2 = 25 — 10h + h 2 + 25 — 10k + k 2
- 8 — 4k — 4h = 50 — 10h — 10k
- 6k + 6h = 42
Подставив значение k=3 в уравнение
Получаем координаты точки центра (h,k) = ( 4,3 )
Шаг :4
Подставим значения h,k в формулу
- r 2 = (x — h) 2 + (y — k) 2
- r 2 = (2 — 4) 2 + (2 — 3) 2
- r 2 = (-2) 2 + (-1) 2
- r 2 = 5
- r = 2.24
Шаг :5
Подставим значения h, k в уравнение окружности
(x — h) 2 + (y — k) 2
Уравнение окружности = (x — 4) 2 + (y — 3) 2
График окружности по трем точкам
Уравнение окружности, проходящей через три заданные точки
Этот онлайн калькулятор выводит уравнение окружности, проходящей через три заданные точки
Этот онлайн-калькулятор находит окружность, проходящую через три заданные точки. Калькулятор находит центр, радиус и уравнение окружности, и строит окружность на графике. Методы, использованные для нахождения центра и радиуса окружности, описаны ниже под калькулятором.
Уравнение окружности, проходящей через три заданные точки
Первая точка
Вторая точка
Третья точка
Центр
Как найти окружность, проходящюю через три заданные точки
Давайте вспомним как выглядит уравнение окружности в стандартной форме:
Так как все три точки принадлежат одной окружности, мы можем записать систему уравнений
Значения , и мы знаем. Давайте сделаем подстановку с неизвестными переменнами a, b и c.
Теперь у нас есть три линейных уравнения для трех неизвестных — составим систему уравнений соответствующую матричной форме:
Мы можем решить эту систему уравнений, используя, к примеру, Гауссово исключение. (подробнее прочитать об этом можно здесь — Решение системы линейных алгебраических уравнений методом Гаусса ). «Нет решений» — означает, что точки коллинеарны и окружность через них провести нельзя.
Координаты центра окружность и ее радиус относится к подобному решению
Зная центр и радиус, мы можем получить уравнение окружности, используя этот калькулятор — Уравнение окружности по заданному центру и радиусу в различных формах
Уравнение окружности по трем точкам
Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.
Уравнение окружности
r 2 = (x — h) 2 + (y — k) 2
- h,k — координаты центра Окружности
- x,y — координаты точки окружности
- r — радиус
Пример
Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)
Решение :
Подставляем координаты точек в формулу
- (2 — h) 2 + (2 — k) 2 = r 2
- (2 — h) 2 + (4 — k) 2 = r 2
- (5 — h) 2 + (5 — k) 2 = r 2
Шаг :2
Найдем значение k упрощая 1 и 2 уравнения
- (2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
- 4 — 4h + h 2 + 4 — 4k + k 2 = 4 — 4h + h 2 +16 — 8k + k 2
- 8 — 4k = 20 — 8k
- k= 3
Шаг :3
Найдем значение h упрощая уравнения 2 и 3
- (2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
- 4 — 4h + h 2 + 4 — 4k + k 2 = 25 — 10h + h 2 + 25 — 10k + k 2
- 8 — 4k — 4h = 50 — 10h — 10k
- 6k + 6h = 42
Подставив значение k=3 в уравнение
Получаем координаты точки центра (h,k) = ( 4,3 )
Шаг :4
Подставим значения h,k в формулу
- r 2 = (x — h) 2 + (y — k) 2
- r 2 = (2 — 4) 2 + (2 — 3) 2
- r 2 = (-2) 2 + (-1) 2
- r 2 = 5
- r = 2.24
Шаг :5
Подставим значения h, k в уравнение окружности
(x — h) 2 + (y — k) 2
Уравнение окружности = (x — 4) 2 + (y — 3) 2
Определить формулу окружности по трем точкам
| Три точки по которым необходимо построить окружность |
| Первая координата |
| Вторая координата |
| Третья координата |
Полученная формула окружности
Напомним, что общее уравнение кривой второго порядка выглядит так
Частные примеры кривой второго порядка это и парабола и гибербола и окружность и прямая линия.
Формула окружности с центром (a;b) и радиусом R имеет вид
или если мы раскроем скобки
из этого уравнения мы можем видеть что кривая второго порядка превращается в формулу окружности если
Из этого же мы можем утверждать, что для построения окружности нам нужно как минимум три точки, так как у нас из всех шести вышеуказанных коэффициентов, только три коэффицента неизвестны.
Бот, позволяет Вам рассчитывать формулу окружности по заданным трем точкам.
Если бы бота не было, то Вам пришлось бы решать систему уравнений из трех переменных, что не очень удобно и трудоёмко.
Интересные факты
Если Вам известны все коэффициенты кривой второго порядка , которые выражают окружность ( ), то очень легко по ним определить два основных параметра:центр окружности и радиус окружности
Центр окружности
Радиус окружности
Синтаксис
Так как это частный пример уже созданного бота то просто расскажем о нюансах
kp2 1 1 0 координаты точек
Где координаты точек есть представление в виде x:y (х-абсцисса, y-ордината)
Каждая координата точки, должна разделятся как минимум одним пробелом.
Что же такое 1 1 0 ? Это уже известные нам коэффициенты при общей формуле.
Примеры
Составить уравнение окружности, проходящей через точки (3,1) (-2,6) и (-5,-3)
Так и запишем kp2 1 1 0 3:1 -2:6 -5:-3
[spoiler title=”источники:”]
http://planetcalc.ru/8116/
http://b4.cooksy.ru/articles/okruzhnost-i-radius-okruzhnosti-po-trem-tochkam
[/spoiler]
Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.
Уравнение окружности
r2 = (x — h)2 + (y — k)2
где,
- h,k — координаты центра Окружности
- x,y — координаты точки окружности
- r — радиус
Пример
Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)
Решение :
Шаг:1
Подставляем координаты точек в формулу
- (2 — h)2 + (2 — k)2 = r2
- (2 — h)2 + (4 — k)2 = r2
- (5 — h)2 + (5 — k)2 = r2
Шаг :2
Найдем значение k упрощая 1 и 2 уравнения
- (2 — h)2 + (2 — k)2 = (2 — h)2 + (4 — k)2
- 4 — 4h + h2+ 4 — 4k + k2 = 4 — 4h + h2+16 — 8k + k2
- 8 — 4k = 20 — 8k
- k=3
Шаг :3
Найдем значение h упрощая уравнения 2 и 3
- (2 — h)2 + (2 — k)2 = (5 — h)2 + (5 — k)2
- 4 — 4h + h2+ 4 — 4k + k2 = 25 — 10h + h2+ 25 — 10k + k2
- 8 — 4k — 4h = 50 — 10h — 10k
- 6k + 6h = 42
Подставив значение k=3 в уравнение
- 6h = 24
- h=4
Получаем координаты точки центра (h,k) = (4,3)
Шаг :4
Подставим значения h,k в формулу
- r2 = (x — h)2 + (y — k)2
- r2 = (2 — 4)2 + (2 — 3)2
- r2 = (-2)2 + (-1)2
- r2 = 5
- r = 2.24
Шаг :5
Подставим значения h, k в уравнение окружности
(x — h)2 + (y — k)2
Уравнение окружности = (x — 4)2 + (y — 3)2
Ответ :
- Координаты точки центра окружности c(h,k) = c(4,3)
- Радиус окружности r = 2.24
- Уравнение окружности = (x — 4)2 + (y — 3)2 = (2.24)2
людей нашли эту статью полезной. А Вы?
Этот онлайн-калькулятор находит окружность, проходящую через три заданные точки. Калькулятор находит центр, радиус и уравнение окружности, и строит окружность на графике. Методы, использованные для нахождения центра и радиуса окружности, описаны ниже под калькулятором.
Уравнение окружности, проходящей через три заданные точки
Первая точка
Вторая точка
Третья точка
Точность вычисления
Знаков после запятой: 2
Центр
Стандартное уравнение окружности
Общее уравнение окружности
Параметрическое уравнение окружности
Как найти окружность, проходящюю через три заданные точки
Давайте вспомним как выглядит уравнение окружности в стандартной форме:
Так как все три точки принадлежат одной окружности, мы можем записать систему уравнений
Значения ,
и
мы знаем. Давайте сделаем подстановку с неизвестными переменнами a, b и c.
Теперь у нас есть три линейных уравнения для трех неизвестных – составим систему уравнений соответствующую матричной форме:
Мы можем решить эту систему уравнений, используя, к примеру, Гауссово исключение. (подробнее прочитать об этом можно здесь – Решение системы линейных алгебраических уравнений методом Гаусса ). “Нет решений” – означает, что точки коллинеарны и окружность через них провести нельзя.
Координаты центра окружность и ее радиус относится к подобному решению
Зная центр и радиус, мы можем получить уравнение окружности, используя этот калькулятор – Уравнение окружности по заданному центру и радиусу в различных формах
Как найти радиус круга
2 методика:Вычисление радиуса по основным величинамВычисление радиуса по трем точкам на окружности
Радиус круга – отрезок, соединяющий центр круга с любой точкой на его окружности. Значение радиуса используется для вычисления длины окружности, площади круга, диаметра окружности, а также при нахождении объема трехмерных фигур, например, объема цилиндра. Радиус круга равен d/2, где d – диаметр круга; C/2π, где C – длина окружности; √(A/π), где A – площадь круга.
Шаги
Метод 1 из 2: Вычисление радиуса по основным величинам
Определение основных величин
-
1
Радиус можно найти по известным значениям основных величин круга/окружности. К таким величинам относятся:- Длина окружности (C).
- Диаметр (D) (отрезок, соединяющей две точки на окружности и проходящий через центр круга).
- Радиус (R) (отрезок, соединяющий центр круга с любой точкой на окружности).
- Площадь (A) (пространство, ограниченное окружностью).
- Число Пи (π) (математическая постоянная, представляющая отношение длины окружности к ее диаметру; это число применяется при вычислении всех основных величин круга и обычно округляется до 3,14).
-
2
Ниже приведены формулы для вычисления диаметра, длины окружности и площади круга; каждая из них включает радиус. Запомните: обособив радиус на одной стороне формулы, вы сможете найти его по известным значениям основных величин круга/окружности.- D = 2r. Диаметр вдвое больше радиуса.
- С = πD = 2πr. Длина окружности равна произведению π на ее диаметр. Так как диаметр в два раза больше радиуса, то длина окружности равна произведению π на двойку и на радиус этой окружности.
- A = πr^2. Площадь круга равна произведению квадрата его радиуса на π.
Вычисление радиуса по формулам
-
1
Если вам дан диаметр, разделите его пополам (на 2) и получите радиус. Так как D = 2r, то r =D/2.- Например, если диаметр круга равен 10 м, то радиус круга равен 10/2 = 5 м.
-
2
Если вам дана длина окружности, разделите ее на 2π и получите радиус. Так как C = 2πr, то r = C/2π.- Например, если длина окружности равна 10 см, то сначала разделите это значение на π: 10/π = 3,14 см. Теперь разделите полученное значение на 2, чтобы вычислить радиус: 3,14/2 = 1,59 см.
-
3
Если вам дана площадь круга, разделите ее на π и из полученного значения извлеките квадратный корень, чтобы найти радиус. Так как А = πr2, то r = √(A/π).- Например, площадь круга равна 10 м2. Сначала разделите это значение на π: 10/π = 3,14. Теперь из полученного значения извлеките квадратный корень, чтобы найти радиус: √3,14 = 1,78 м.
Метод 2 из 2: Вычисление радиуса по трем точкам на окружности
-
1
Если вам не даны значения диаметра, длины окружности или площади круга, вы можете вычислить радиус круга по координатам трех точек на окружности (назовем их P1, P2 и P3). Это делается при помощи одной из двух формул, приведенных ниже.- Формулы для нахождения радиуса круга по трем точкам, лежащем на окружности:
- (abc)/(√(a + b + c)(b + c – a)(c + a – b)(a + b – c)), где a, b, c – стороны треугольника с вершинами в точках P1, P2, P3.[1]
- a/(2sin(θ)), где a –сторона треугольника с вершинами в точках P1, P2, P3; θ – противолежащий угол.
- Во второй формуле вам нужно знать только координаты двух точек и угол; если угол не дан, вам понадобятся координаты всех трех точек.
- Формулы для нахождения радиуса круга по трем точкам, лежащем на окружности:
-
2
Найдите расстояние между каждыми двумя точками, чтобы определить значения сторон треугольника. Для этого подставьте известные вам координаты в формулу: Расстояние = √((x2 – x1)2 + (y2 – y1)2), где x1,y1 – координаты первой точки; x2,y2 – координаты второй точки.- Пример. На окружности круга лежат точки с координатами (3,0), (3,8) и (-1, 4). Найдите расстояние между точками (3,8) и (-1,4) по следующей формуле (то есть вы находите сторону треугольника):
- √((x2 – x1)2 + (y2 – y1)2)
- √((-1 – 3)2 + (4 – 8)2)
- √((-4)2 + (-4)2)
- √(16 + 16) = √(32) = 5,66
- Пример. На окружности круга лежат точки с координатами (3,0), (3,8) и (-1, 4). Найдите расстояние между точками (3,8) и (-1,4) по следующей формуле (то есть вы находите сторону треугольника):
-
3
Найдите расстояние между двумя другими парами точек (то есть найдите две другие стороны треугольника) при помощи процесса, описанного в предыдущем шаге. Подставьте известные вам координаты в ту же формулу: Расстояние = √((x2 – x1)2 + (y2 – y1)2).- В нашем примере вам необходимо найти расстояние между точками (3,0) и (3,8) и между точками (3,0) и (-1, 4). В первой паре меняется только координата «у», поэтому расстояние равно 8. Расстояние между второй парой точек вычислите следующим образом:
- √((x2 – x1)2 + (y2 – y1)2)
- √((-1 – 3)2 + (4 – 0)2)
- √((-4)2 + (4)2)
- √(16 + 16) = √(32) = 5,66. Таким образом, стороны треугольника равны 5,66; 8; 5,66.
- В нашем примере вам необходимо найти расстояние между точками (3,0) и (3,8) и между точками (3,0) и (-1, 4). В первой паре меняется только координата «у», поэтому расстояние равно 8. Расстояние между второй парой точек вычислите следующим образом:
-
4
Воспользуйтесь формулой (abc)/(√(a + b + c)(b + c – a)(c + a – b)(a + b – c)) для вычисления радиуса круга (a, b, c – стороны треугольника). Для этого подставьте в эту формулу найденные вами стороны треугольника.- В нашем примере а = 5,66; b = 8; с = 5,66.
- (abc)/(√(a + b + c)(b + c – a)(c + a – b)(a + b – c))
- ((5,66)(8)(5,66))/(√(5,66 + 8 + 5,66)(8 + 5,66 – 5,66)(5,66 + 5,66 – 8)(5,66 + 8 – 5,66))
- (256,28)/(√(19,32)(8)(3,32)(8))
- (256,28)/(√(4105,11))
- (256,28)/(64,07) = 4. Радиус нашего круга равен 4. Этот ответ верный, потому что сторона треугольника, равная 8, проходит через центр круга, то есть это его диаметр. Так как радиус равен половине диаметра, то 8/2 = 4.
- В нашем примере а = 5,66; b = 8; с = 5,66.
-
5
Теперь найдем угол, противолежащий найденной стороне треугольника, по формуле (теорема косинусов): c2 = a2 + b2 – 2abCos(θ), где a, b, c – стороны треугольника, θ – угол между сторонами а и b, противолежащий стороне с. Найдя противолежащий угол, вы можете вычислить радиус по формуле: a/(2sin(θ))).- В нашем примере а = 5,66; b = 8; с = 5,66. Найдем угол, противолежащий первой стороне.
- c2 = a2 + b2 – 2abCos(θ)
- 5,662 = 5,662 + 82 – 2(5,66)(8)Cos(θ)
- 32,04 = 32,04 + 64 – 90,56Cos(θ)
- -64 = – 90,56Cos(θ)
- 0.707 = Cos(θ)
- θ = 45o (для нахождения угла необходимо вычислить arcos).
- В нашем примере а = 5,66; b = 8; с = 5,66. Найдем угол, противолежащий первой стороне.
-
6
Подставьте известные вам значения стороны треугольника и противолежащего угла в формулу а/(2sin(θ)), чтобы найти радиус круга. Эта формула выведена из теоремы синусов, которая гласит, что отношение стороны треугольника к ее противолежащему углу равно удвоенному радиусу (или диаметру) окружности, описанной вокруг треугольника, то есть а/sin(θ) = 2r.[2]- В нашем примере сторона равна 5,66, а противолежащий угол равен 45o. Подставьте эти значения в формулу.
- a/(2sin(θ))
- 5,66/(2sin(45o))
- 5,66/ 2(0,707)
- 5,66/1,414 = 4. Обратите внимание, что вы получили такое же значение радиуса, как и при использовании формулы ((abc)/(√(a + b + c)(b + c – a)(c + a – b)(a + b – c))).
- В нашем примере сторона равна 5,66, а противолежащий угол равен 45o. Подставьте эти значения в формулу.
Советы
- Пользуйтесь калькулятором для проверки ответа.
- Для получения более точных результатов на калькуляторе используйте клавишу π.
Координаты центра окружности по трем точкам
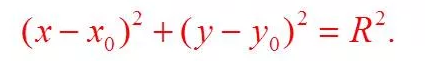
Обычно эта задача решается через уравнения круга, но для программирования нужно аналитическое решение (в виде формулы).
Если решать систему уравнений, пытаясь выразить все неизвестные величины через 6 координат известных точек, то можно получить выражения для Xo, Yo и R.
Но вид этих выражений и их последующая реализация в виде программного кода — мягко говоря — не вдохновляют начинать эту работу.
К счастью, есть алгебраический метод, сводящийся к ряду несложных поэтапных расчетов, которые позволяют вычислить искомые неизвестные.
Ниже прилагаю реализацию этого подхода в виде функции на javascript.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
// на входе функция ожидает массив Z // с тремя точками-объектами вида {x: координата X, y: координата Y} // на выходе получим X, Y, R – центр круга и его радиус function getCircle(Z) { var A = Z[1].x – Z[0].x; var B = Z[1].y – Z[0].y; var C = Z[2].x – Z[0].x; var D = Z[2].y – Z[0].y; var E = A * (Z[0].x + Z[1].x) + B * (Z[0].y + Z[1].y); var F = C * (Z[0].x + Z[2].x) + D * (Z[0].y + Z[2].y); var G = 2 * (A * (Z[2].y – Z[1].y) – B * (Z[2].x – Z[1].x)); if (G == 0) { // если точки лежат на одной линии, // или их координаты совпадают, // то окружность вписать не получится return []; } // координаты центра var Cx = (D * E – B * F) / G; var Cy = (A * F – C * E) / G; // радиус var R = Math.sqrt(Math.pow(Z[0].x – Cx, 2) + Math.pow(Z[0].y – Cy, 2)); // вернем параметры круга return [Cx, Cy, R]; } |
Для тех кому сложно читать код, и нужна чистая математика, привожу алгоритм рассчета:
Даны точки X(x1, y1), Y(x2, y3), Z(x3,y3), принадлежащие окружности с радиусом R и центром U(Cx, Cy).
|
A = x2 – x1; B = y2 – y1; C = x3 – x1; D = y3 – y1; E = A * (x1 + x2) + B * (y1 + y2); F = C * (x1 + x3) + D * (y1 + y3); G = 2 * (A * (y3 – y2) – B * (x3 – x2)); Если G = 0, это значит, что через данный набор точек провести окружность нельзя. Cx = (D * E – B * F) / G; Cy = (A * F – C * E) / G; |
Ну и останется найти радиус — как расстояние между одной из данных точек и найденным центром окружности.
Немного математики
Написать комментарий
Данная запись опубликована в 11.10.2019 02:36 и размещена в Программирование.
Вы можете перейти в конец страницы и оставить ваш комментарий.
Мало букафф? Читайте есчо !
Олимпиада для пятиклашек
Ноябрь 11, 2012 г.
Дочери (5й класс) на каникулы дали типа олимпиадки порешать. По математике. Ясно, что решают в итоге родители. Хорошо тем, кто в НИИ каком нить работает, или, может, профессорá, завалящиеся доценты с техническим уклоном имеются под рукой. А что делать …
Читать
Магия чисел
Февраль 14, 2011 г.
Старшая дочь у меня уже ходит в 3й класс общеобразовательной средней школы. Склад ума у неё не лежит к точным наукам, но пока это не мешает ей приносить …
Читать












