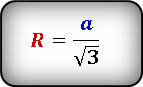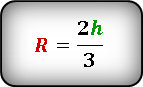Как найти радиус окружности в треугольнике равностороннем

Радиус описанной окружности равностороннего треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

Свойства равностороннего треугольника

Свойство 1. В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }})

Естественно, не правда ли? Три одинаковых угла, в сумме ({{180}^{o }}), значит, каждый по ({{60}^{o }})

Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).

Почему так? А посмотрим-ка на равносторонний треугольник.

Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.

Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!

В равностороннем треугольнике оказалось не (12) особенных линий, как во всяком обычном треугольнике, а всего три!

Итак, ещё раз:

Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.

Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. (R=2cdot r)

Уже должно быть очевидно, отчего так.

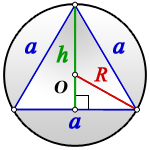
Посмотри на рисунок: точка( O) – центр треугольника.

Значит, (OB) – радиус описанной окружности (обозначили его (R)), а (OK) – радиус вписанной окружности (обозначим (r)).

Но ведь точка (O) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении (2:1), считая от вершины.

Поэтому (OB=2cdot OK), то есть (R=2cdot r).

Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.

Давай удостоверимся в этом.

Равносторонний треугольник – это треугольник, у которого все стороны равны.

Другие виды треугольников:

• прямоугольные треугольники;
• равнобедренные треугольники.

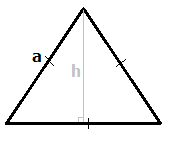
Любой равносторонний треугольник характеризуется стороной a (см. рисунок). При решении задач могут понадобиться высота h, радиусы вписанной (r) и описанной (R) окружности. Именно эти характеристики используются в формулах равностороннего треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.

Формула радиуса вписанной окружности для равностороннего треугольника

Радиус вписанной окружности r можно вычислить, зная сторону равностороннего треугольника:

r = a/(2√3)

Формула радиуса описанной окружности для равностороннего треугольника

Радиус описанной окружности R можно вычислить, зная сторону равностороннего треугольника:

R = a/(√3)

Формула периметра равностороннего треугольника

Периметр P равностороннего треугольника можно получить, зная его сторону:

P = 3a

Формулы площади равностороннего треугольника

p>При вычислении площади равностороннего треугольника можно использовать формулы, которые применяются для вычисления площади произвольного треугольника, так как равносторонний треугольник является частным случаем произвольного треугольника.

Площадь равностороннего треугольника S можно вычислить, зная его сторону a:

S = (√3 ⋅ a²)/4

Площадь равностороннего треугольника S также можно вычислить, зная его высоту h:

S = h²/√3

Если в задаче присутствует окружность, вписанная в треугольник, площадь равностороннего треугольника можно вычислить через радиус окружности r:

S = 3√3 ⋅ r²

Если в задаче присутствует окружность, описанная вокруг треугольника, площадь равностороннего треугольника можно вычислить через радиус окружности R:

S = (3√3 ⋅ R²)/4

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства[править | править код]

Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.

• Радиус вписанной окружности правильного треугольника, выраженный через его сторону:

• Радиус описанной окружности правильного треугольника, выраженный через его сторону:

• Периметр правильного треугольника:

• Высоты, медианы и биссектрисы правильного треугольника:

• Площадь правильного треугольника рассчитывается по формулам:

• Радиус описанной окружности равен двойному радиусу вписанной окружности:

• Правильными треугольниками можно замостить плоскость.

• В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.

Правильный сферический треугольник[править | править код]

Для любого значения в интервале от 60 до 180 градусов существует правильный сферический треугольник с равными этому значению углами.

Теоремы о равностороннем треугольнике или содержащие его[править | править код]

• Задача Наполеона
• Прямая Симсона одно из свойств
• Теорема Вивиани
• Теорема Морли
• Теорема Наполеона
• Теорема Помпею
• Теоремы Тебо 2 и 3
• Точки Аполлония
• Точки Торричелли

См. также[править | править код]

• Замечательные прямые треугольника
• Замечательные точки треугольника
• Равнобедренный треугольник
• Теорема Чевы
• Треугольник
• Треугольник Рёло

Примечания[править | править код]

Символ Шлефли
Многоугольники	{1} {2} {3} {4} {5} {6} {7} {8} {9} {10} {11} {12} {14} {15} {17} {18} {20} {30} {51}[de] {257} {65537} {4294967295} {∞}
Звёздчатые многоугольники	{5/2} {6/2} {7/2} {7/3} {8/2} {8/3} {9/2} {9/3} {9/4}
Паркеты на плоскости	{3,6} {4,4} {6,3}
Правильные многогранники и сферические паркеты	{2,n} {3,3} {4,3} {3,4} {5,3} {3,5} {n,2}
Многогранники Кеплера — Пуансо	{5/2,5} {5,5/2} {5/2,3} {3,5/2}
Соты	{4,3,4}
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}