Радиус описанной окружности шестиугольника, формула
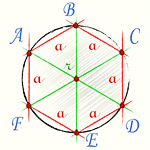
Для расчета радиуса описанной окружности шестиугольника используем формулу радиуса описанной окружности правильного многоугольника
[R = frac{a}{2 sin(frac{360°}{12})} = frac{a}{2 sin(30°)} = a]
(a – сторонa правильного шестиугольника; R – радиус описанной окружности правильного шестиугольника)
Также можно пойти другим путем. Если соединить все вершины правильного шестиугольника через центр, станет видно, что правильный шестиугольник состоит из 6-ти правильных треугольников, т.е.
[R = frac{a}{2 sin(π/6)} = a]
Вычислить, найти радиус описанной окружности шестиугольника по формуле (2)
Радиус описанной окружности шестиугольника |
стр. 253 |
|---|
Шестиугольник является правильным многоугольником, так как у него все стороны и углы равны. А значит, около любого шестиугольника можно описать окружность.
 Точка O –центр правильного многоугольника, также является центром описанной вокруг него окружности.
Точка O –центр правильного многоугольника, также является центром описанной вокруг него окружности.
Центр правильного многоугольника равноудален от его вершин. Отрезок, соединяющий центр с вершинами называется радиусом правильного многоугольника и также является радиусом описанной около него окружности.
Формула радиуса описанной окружности около шестиугольника
Существует классическая формула для нахождения радиуса описанной окружности около правильного многоугольника

Для правильного шестиугольника n=6, тогда угол будет равен 
По тригонометрической таблице sin(30°)=
Тогда формула радиуса описанной окружности около шестиугольника имеет следующий вид
Радиус описанной окружности около шестиугольника равен его стороне

![]() Пример расчета радиуса окружности описанной около шестиугольника
Пример расчета радиуса окружности описанной около шестиугольника
Найдите радиус окружности описанной около правильного шестиугольника, если радиус вписанной окружности в него равен
Радиус описанной окружности около шестиугольника имеет вид R = a
Применив формулу радиуса вписанной окружности в шестиугольник, получаем: 
Выразим сторону шестиугольника: 
Выразим радиус описанной окружности через радиус вписанной: 
Радиус описанной окружности правильного шестиугольника
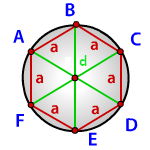
a – сторона шестиугольника
d – диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 20 мая 2017
Радиус описанной окружности шестиугольника
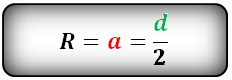
Если у шестиугольника как углы, так и стороны равны, соответственно, это — правильный многоугольник, вокруг которого можно описать лишь одну окружность. Все вершины шестиугольника лежат на описанной вокруг него окружности. У правильного шестиугольника центр расположен на равном расстоянии от его вершин. Центр шестиугольника и центр описанной окружности совпадают. Линия, которая соединяет центр с вершинами, считается радиусом как многоугольника, так и описанной окружности. В правильном шестиугольнике сторона и радиус равны. Отсюда, R описанной окружности равняется его стороне или диагонали, поделенной пополам:
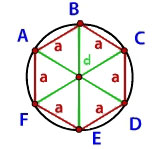
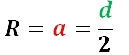
В данном выражении:
а — величина стороны шестиугольника;
R — величина радиуса;
d — диагональ.
Онлайн калькулятор поможет быстро и правильно найти величину радиуса, для этого вам нужно лишь занести исходные данные.
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников. 
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;
каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ) .
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/pravilnyj-shestiugolnik-i-ego-ploshhad/
http://shkolkovo.net/theory/77
[/spoiler]
Радиус описанной окружности шестиугольника
Радиус описанной окружности
Если у шестиугольника как углы, так и стороны равны, соответственно, это — правильный многоугольник, вокруг которого можно описать лишь одну окружность. Все вершины шестиугольника лежат на описанной вокруг него окружности. У правильного шестиугольника центр расположен на равном расстоянии от его вершин. Центр шестиугольника и центр описанной окружности совпадают. Линия, которая соединяет центр с вершинами, считается радиусом как многоугольника, так и описанной окружности. В правильном шестиугольнике сторона и радиус равны. Отсюда, R описанной окружности равняется его стороне или диагонали, поделенной пополам:

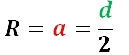
В данном выражении:
а — величина стороны шестиугольника;
R — величина радиуса;
d — диагональ.
Онлайн калькулятор поможет быстро и правильно найти величину радиуса, для этого вам нужно лишь занести исходные данные.
