Как найти радиус описанного круга трапеции

Как найти радиус описанного круга трапеции

Как найти радиус описанной окружности для трапеции?

В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.

I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции

Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.

В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул

    [R = frac{a}{{2sin alpha }},]

где a — сторона треугольника, α — противолежащий ей угол;

либо по формуле

    [R = frac{{abc}}{{4S}},]

где a, b, c — стороны, S — площадь треугольника.

radius-opisannoj-okruzhnosti-dlya-trapecii

Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:

    [R = frac{{AD cdot AB cdot BD}}{{4{S_{Delta ABD}}}}]

или

    [R = frac{{BD}}{{2sin angle A}},]

где синус угла A можно найти из прямоугольного треугольника ABF:

    [sin angle A = frac{{BF}}{{AB}}]

III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров

radius-opisannoj-okruzhnosti-v-trapeciiРадиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).

Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.

Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить

    [B{O^2} = B{K^2} + O{K^2}]

    [A{O^2} = A{N^2} + O{N^2}]

и приравнять правые части

    [A{O^2} = B{O^2} = {R^2}, Rightarrow ]

    [A{N^2} + O{N^2} = B{K^2} + O{K^2}]

    [{(frac{a}{2})^2} + {x^2} = {(frac{b}{2})^2} + {(h - x)^2}]

Решив это уравнения относительно x, можно найти R.

IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.

centr-opisannoj-okruzhnosti-na-osnovanii-trapecii

    [AC bot CD, Rightarrow ]

точка O — середина AD

    [R = frac{1}{2}AD]

centr-opisannoj-okruzhnosti-lezhit-vne-trapeciiЕсли диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.

I вариант нахождения радиуса для этого случая не изменяется.

centr-opisannoj-okruzhnosti-vne-trapeciiВо II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.

Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.

Источник

Свойства окружности, описанной вокруг трапеции

Содержание:

  • Окружность, описанная около трапеции
  • Как найти радиус описанной окружности

    • Если известны угол и диагональ трапеции
    • Если известны диагональ, стороны трапеции и площадь одного из треугольников
    • Если известны длины сторон треугольника
  • Как найти центр описанной окружности

    • Если угол прямой
    • Если угол острый
    • Если угол тупой
  • Задачи с решениями

Окружность, описанная около трапеции

Трапеция — это выпуклый четырехугольник, две стороны которого параллельны, а две другие — не параллельны.

Около четырехугольника можно описать окружность, если сумма его противолежащих углов равна 180°. Поэтому окружность можно описать только вокруг равнобедренной трапеции.

Окружность, описанная около трапеции

Как найти радиус описанной окружности

Самый распространенный способ найти радиус окружности, описанной около трапеции — через радиус окружности, описанной около треугольника, имеющего 3 любые общие вершины с данной трапецией.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Каждая диагональ делит трапецию на два треугольника. Описанная окружность проходит через все вершины трапеции, значит она проходит через все вершины каждого из этих треугольников и также является для них описанной окружностью.

Как найти радиус описанной окружности

Если известны угол и диагональ трапеции

Формула 1

(R=frac а{2cdotsinalpha},)

где R — радиус описанной окружности,

а — сторона треугольника,

α — угол треугольника, противолежащий стороне а.

Например, если известна диагональ BD=а и острый угол трапеции ABCD ∠CDA=β, то можем найти радиус описанной окружности.

Рассмотрим треугольник BCD. Сторона BD известна. (∠BCD=180°-∠CDA=180°-β). 

Радиус описанной окружности будет равен (frac а{2cdotsinleft(180^circ-betaright)}).

Если известны диагональ, стороны трапеции и площадь одного из треугольников

Формула 2

(R=frac{abc}{4S}),

где R — радиус описанной окружности,

а, b, c — стороны треугольника,

S — площадь треугольника.

Если известны длины сторон треугольника

Формула 3

(R=frac{abc}{4sqrt{pleft(p-aright)left(p-bright)left(p-cright)}},)

где R — радиус описанной окружности,

а, b, c — стороны треугольника,

p — ½ периметра треугольника.

Как найти центр описанной окружности

Центр описанной окружности может лежать как внутри трапеции, так и вне ее. Определить его местонахождение помогает угол между диагональю трапеции и боковой стороной.

Если угол прямой

Если угол прямой

Если диагональ трапеции перпендикулярна ее боковой стороне, то центр описанной окружности будет лежать на середине большего основания. Тогда большее основание будет равно диаметру описанной окружности.

Формула 4

(R=frac12а,)

где R — радиус описанной окружности,

а — большее основание трапеции.

Если угол острый

Если угол острый

Если диагональ трапеции и боковая сторона образуют острый угол, то центр описанной около трапеции окружности лежит внутри трапеции.

Если угол тупой

Если угол тупой

Если диагональ трапеции и боковая сторона образуют тупой угол, то центр описанной около трапеции окружности будет лежать вне трапеции за ее большим основанием.

Задачи с решениями

Задача

Дано: трапеция с описанной окружностью. Периметр трапеции равен 22 см, а ее средняя линия — 5 см.

Найти: боковую сторону трапеции.

Решение: Так как около трапеции описана окружность, эта трапеция — равнобедренная. Удвоенная средняя линия трапеции равна сумме ее оснований (10 см). Сумма двух боковых сторон равна 22-10=12 (см). Боковая сторона трапеции равна 6 см.

Ответ: 6 см.

Примечание

Задача

Дано: основания трапеции ВС=11 см и AD=21 см. Диагональ трапеции ВD=20 см.

Найти: радиус описанной окружности.

Решение: найдем радиус окружности, описанной около (ΔABD. R=frac{BD}{2sinangle A}.)

  1. Трапеция ABCD равнобедренная, AB=CD, так как описать окружность можно только около равнобедренной трапеции.
  2. ВЕ — высота трапеции. Отрезок (АЕ=(21-11):2=5 (см)) по свойству равнобедренной трапеции. Отрезок ЕD=21-5=16 (см).
  3. Треугольник BED прямоугольный. ∠BED=90°. По теореме Пифагора (BE=sqrt{20^2-16^2}=12 (см).)
  4. Треугольник АBE также прямоугольный. ∠BED=90°. По теореме Пифагора (АВ=sqrt{5^2+12^2}=13 (см).)
  5. (sin∠BAD=frac{12}{13}) по определению синуса.
  6. (R=frac{BD}{2sinangle A}=10frac56 (см).)

Ответ: (10frac56 см.)

Источник

Радиус описанной окружности трапеции, формула

Радиус описанной окружности трапеции
Для нахождения радиуса описанной окружности трапеции делают дополнительные построения — строят диагональ трапеции — BD.
Теперь трапеция разбита на два треугольника ABD и BСD. Окружность при этом описана вокруг обоих этих треугольников. Далее по известным параметрам трапеции находим недостающие стороны этих треугольников и по классической формуле радиуса описанной окружности треугольника находим радиус описанной окружности трапеции:

[R = frac{adc}{4sqrt{p(p-a)(p-d)(p-c)}}]

где

[p=frac{1}{2}(a+d+c)]

(a (BC), d (BD), c (CD) – стороны треугольника; R – радиус описанной окружности треугольника)

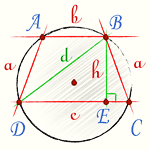
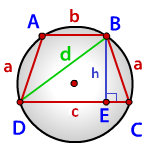
Пусть у нашей равнобокой трапеции заданы основания и высота (см. рисунок ниже), тогда:

[ EC = frac{c-b}{2} \ medspace \ DE = c – frac{c-b}{2} = frac{c+b}{2} ]

по теореме Пифагора найдутся диагональ:

[ BD = d = sqrt{h^2 + Big(frac{c+b}{2}Big)^2} ]

и бедро трапеции:

[ BC = a = sqrt{h^2 + Big(frac{c-b}{2}Big)^2} ]

Вычислить, найти радиус описанной окружности трапеции по формулам (1,2,3,4,5)

Радиус описанной окружности трапеции

 стр. 250
Источник

Радиус описанной окружности равнобокой трапеции

Радиус описанной окружности трапеции

a – боковые стороны трапеции

c – нижнее основание

b – верхнее основание

d – диагональ

p – полупериметр треугольника DBC

p = (a+d+c)/2

Формула радиуса описанной окружности равнобокой трапеции, (R)

Формула радиуса описанной окружности равнобокой трапеции

Калькулятор – вычислить, найти радиус описанной окружности трапеции

Подробности

Автор: Administrator

Опубликовано: 11 сентября 2011

Обновлено: 13 августа 2021

Источник

Окружность можно описать только вокруг равнобокой трапеции, так как сумма ее противоположных углов должна равняться 180°. В равнобокой трапеции углы при основании одинаковы, следовательно, их односторонние углы дополняют их до 180°, включая углы на противоположной стороне. Для того чтобы найти радиус описанной вокруг равнобокой трапеции окружности, нужно провести в трапеции диагональ, которая разделит ее на два треугольника. Таким образом, окружность теперь описывает не только трапецию, но и оба треугольника, и через формулу радиуса окружности, описанной вокруг треугольника, можно получить формулу для радиуса трапеции.

Источник

Добавить комментарий