Как найти радиус описанной окружности этого треугольника - Сайт, где вы сможете решить свои вопросы

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса описанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равносторонний треугольник
Примеры задач

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

Источник

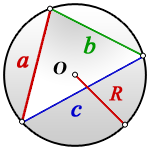
, , c blue – стороны треугольника

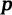– полупериметр

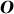O black – центр окружности

Формула радиуса описанной окружности треугольника ( R ) :

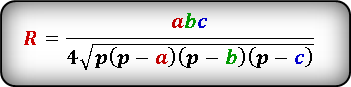
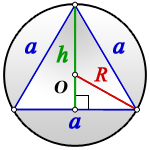
– сторона треугольника

– высота

– радиус описанной окружности

Формула радиуса описанной окружности равностороннего треугольника через его сторону:

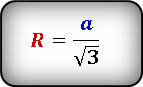
Формула радиуса описанной окружности равностороннего треугольника через высоту:

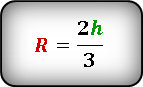
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

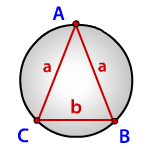
a, b – стороны треугольника

Формула радиуса описанной окружности равнобедренного треугольника(R):

Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

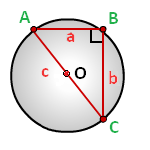
a, b – катеты прямоугольного треугольника

c – гипотенуза

Формула радиуса описанной окружности прямоугольного треугольника (R):

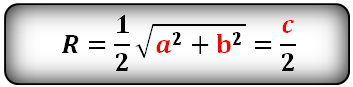
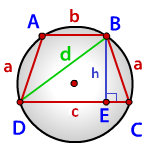
a – боковые стороны трапеции

c – нижнее основание

b – верхнее основание

d – диагональ

p – полупериметр треугольника DBC

p = (a+d+c)/2

Формула радиуса описанной окружности равнобокой трапеции, (R)

Радиус описанной окружности квадрата равен половине его диагонали

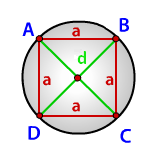
a – сторона квадрата

d – диагональ

Формула радиуса описанной окружности квадрата (R):

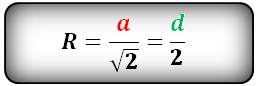
Радиус описанной окружности прямоугольника равен половине его диагонали

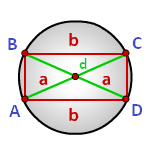
a, b – стороны прямоугольника

d – диагональ

Формула радиуса описанной окружности прямоугольника (R):

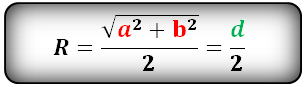
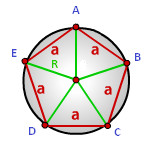
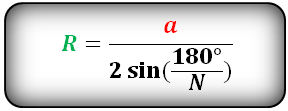
a – сторона многоугольника

N – количество сторон многоугольника

Формула радиуса описанной окружности правильного многоугольника, (R):

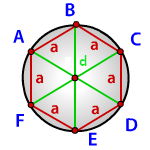
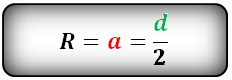
a – сторона шестиугольника

d – диагональ шестиугольника

Радиус описанной окружности правильного шестиугольника (R):

Источник

Радиус описанной около треугольника окружности можно найти по одной из двух общих формул.

Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.

Радиус описанной около произвольного треугольника окружности

Формула I (следствие из теоремы синусов)

$[R = frac{{AB}}{{2sin angle C}} = frac{{BC}}{{2sin angle A}} = frac{{AC}}{{2sin angle B}}]$

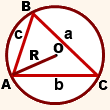
То есть радиус описанной окружности равен отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла.

В общем виде эту формулу записывают так:

$[R = frac{a}{{2sin alpha }} = frac{b}{{2sin beta }} = frac{c}{{2sin gamma }}]$

Формула II.

$[R = frac{{AB cdot BC cdot AC}}{{4{S_{Delta ABC}}}}]$

в общем виде —

$[R = frac{{abc}}{{4S}}]$

То есть чтобы найти радиус описанной около треугольника окружности, надо произведения длин сторон треугольника разделить на четыре площади треугольника.

Если площадь треугольника находить по формуле Герона

где p — полупериметр,

$[p = frac{{a + b + c}}{2},]$

то получим формулу радиуса описанной около треугольника окружности через длины сторон:

$[R = frac{{abc}}{{4sqrt {p(p - a)(p - b)(p - c)} }}.]$

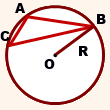
Обе эти формулы можно применить к треугольнику любого вида. Следует только учесть положение центра.

Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника, напротив тупого угла.

Радиус окружности, описанной около прямоугольного треугольника

Формула:

$[R = frac{{AB}}{2}]$

То есть в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.

Обычно гипотенузу обозначают через c (AB=c) и формулу записывают так:

$[R = frac{c}{2}]$

Радиус окружности, описанной около правильного треугольника

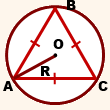
Формула:

$[R = frac{a}{{sqrt 3 }}]$

Если без иррациональности в знаменателе, то

$[R = frac{{asqrt 3 }}{3}]$

В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной окружности:

Источник

Радиус описанной около треугольника окружности

Анна Кирпиченкова

Эксперт по предмету «Калькуляторы»

Задать вопрос автору статьи

В этой статье приведены формулы для расчёта радиуса описанной около треугольника окружности для различных случаев, а именно: для прямоугольного, равнобедренного и равностороннего треугольников.

Также приведена формула для описанной около треугольника окружности в общей форме и добавлены онлайн-калькуляторы для быстрого расчёта.

Определение 1

Описанной около треугольника окружностью называется окружность, внутри которой расположен треугольник, причём все три вершины этого треугольника лежат на окружности.

Ниже приведён онлайн-калькулятор для расчёта радиуса описанной окружности для любого треугольника. Для того чтобы воспользоваться им — введите имеющиеся данные в поля для ввода онлайн-калькулятора.

Радиус описанной около треугольника окружности через стороны

Чтобы определить радиус описанной вокруг треугольника окружности, нужно воспользоваться формулой:

$R = frac{acdot b cdot c}{4 cdot sqrt{P cdot(P – a)cdot(P – c) cdot(P – b)}}$ (1), причём

$P$ — это полупериметр треугольника.

Он определяется по формуле:

$P = frac12 cdot (a + b + c)$, где

$a, b, c$ — стороны треугольника.

Рассмотрим пример на поиск радиуса описанной около треугольника окружности.

Пример 1

Задача

Дан треугольник со сторонами $3, 4, 5$ см. Найдите, чему равен радиус описанной вокруг него окружности.

Решение:

Сосчитаем полупериметр:

$P = frac12 cdot (3 + 4 + 5) = 6$ см.

Теперь воспользуемся формулой (1):

$R = frac{3 cdot 4 cdot 5} {4 cdot sqrt{6 cdot (6 – 3) cdot (6 – 4) cdot (6 — 5)}} = 2,5$ см.

Результат совпадает с ответом онлайн-калькулятора, следовательно, задача решена правильно.

Также существуют формулы для расчёта радиуса описанной около прямоугольного и равнобедренного треугольников окружностей.

Радиус описанной около прямоугольного треугольника окружности через стороны

Для прямоугольного треугольника радиус описанной окружности вычисляется по формуле:

$R = frac12 cdot sqrt{d^2 + b^2}$, здесь

$d, b$ — катеты прямоугольного треугольника.

Радиус описанной около равнобедренного треугольника окружности через стороны

В этом случае радиус окружности определяется по формуле:

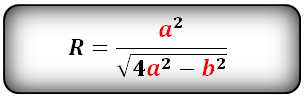
$R = frac{d^2}{sqrt{4d^2 — b^2}}$, здесь

$d$ — длина боковой стороны равнобедренного треугольника;

$b$ — длина основания.

Радиус описанной около равностороннего треугольника окружности через сторону

В этом случае радиус определяется через формулу:

$R = frac{a}{sqrt3}$, здесь

$a$ — сторона равностороннего треугольника.

Рассмотрим в качестве второго примера поиск радиуса описанной окружности через сторону равностороннего треугольника.

Пример 2

Задача

В равностороннем треугольнике сторона $a$ равна $3$ см. Чему равен радиус описанной вокруг него окружности?

Решение:

$R = frac{a}{sqrt3} = 1, 73$ см.

Ответ совпадает с ответом онлайн-калькулятора, а значит, решение найдено верно.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата написания статьи: 18.06.2019

Источник

Радиус описанной окружности около треугольника онлайн

С помощю этого онлайн калькулятора можно найти радиус описанной около треугольника окружности. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Содержание

Радиус окружности описанной около треугольника, если известны три стороны треугольника
Радиус окружности описанной около треугольника, если известны сторона a и противолежащий угол A
Радиус окружности описанной около треугольника, если известны стороны b и c треугольника и угол между ними A
Радиус окружности описанной около треугольника, если известны сторона треугольника a и прилежащие углы B и C

1. Радиус окружности описанной около треугольника, если известны три стороны треугольника

Пусть известны три стороны a, b, c треугольника. Найдем радиус описанной окружности около треугольника.

Площадь треугольника по трем сторонам a, b, c и радиусу R описанной окружности имеет вид:

откуда

Площадь треугольника по трем сторонам имеет вид:

где

Подставляя (2) в (1), получим формулу радиуса описанной окружности около треугольника:

где p вычисляется из формулы (3).

Пример 1. Известны три стороны треугольника: ( small a=6, b=5, c=4.5 ). Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (4), где ( small р ) вычисляется из формулы (3).

Найдем p из (2):

Подставим значения a, b, c, p в (1):

Ответ: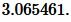

2. Радиус окружности описанной около треугольника, если известны сторона a и противолежащий угол A

Пусть известны сторона a и противолежащий угол A. Найдем радиус описанной окружности около треугольника. Из расширенной теоремы синусов имеем:

Откуда:

Пример 2. Сторона треугольника равна: 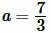а противолежащий угол ( small angle A=35°.) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (5). Подставим значения 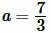и ( small angle A=35° ) в (5):

Ответ: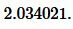

3. Радиус окружности описанной около треугольника, если известны стороны b и c треугольника и угол между ними A

Пусть известны стороны b и c треугольника и угол между ними A. Найдем радиус описанной окружности около треугольника.

Из теоремы косинусов, имеем:

или

Подставляя (6) в (5), получим требуемую формулу:

Пример 3. Известны две стороны треугольника: 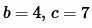и угол между ними: ( small angle A=30°. ) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения 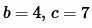и ( small angle A=30° ) в (7):

Ответ: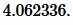

4. Радиус окружности описанной около треугольника, если известны сторона треугольника a и прилежащие углы B и C

Пусть известны сторона a треугольника и прилежащие к ней углы B и C. Найдем радиус описанной окружности около треугольника. Как известно, сумма углов треугольника равна 180°. Поэтому легко найти треий угол треугольника: ( small angle A=180°- (angle B+ nangle C). ) Тогда для нахождения радиуса описанной около треугольника окружности можно воспользоваться формулой (5):

Получили следующую формулу:

Пример 4. Известны сторона треугольника: 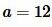и прилежащие к ней углы: ( small angle B=21°, ;angle C=34°. ) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (8). Подставим значения 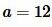и ( small angle B=21°, ;angle C=34° ) в (8):

Ответ: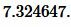

Смотрите также:

Радиус описанной окружности около равнобедренного треугольника онлайн
Радиус описанной окружности около равностороннего треугольника онлайн
Радиус описанной окружности около прямоугольного треугольника онлайн

Источник

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Прямоугольный треугольник

Равносторонний треугольник

Примеры задач

Радиус описанной около треугольника окружности

Радиус описанной около треугольника окружности через стороны

Радиус описанной около прямоугольного треугольника окружности через стороны

Радиус описанной около равнобедренного треугольника окружности через стороны

Радиус описанной около равностороннего треугольника окружности через сторону

Радиус описанной окружности около треугольника онлайн

1. Радиус окружности описанной около треугольника, если известны три стороны треугольника

2. Радиус окружности описанной около треугольника, если известны сторона a и противолежащий угол A

3. Радиус окружности описанной около треугольника, если известны стороны b и c треугольника и угол между ними A

4. Радиус окружности описанной около треугольника, если известны сторона треугольника a и прилежащие углы B и C

Вам также может понравиться

Как найти жесткий диск в биосе gigabyte

Как быстро найти комету в draconic evolution

Как найти разность фаз между напряжениями

Добавить комментарий Отменить ответ