Радиус описанной окружности прямоугольного треугольника
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
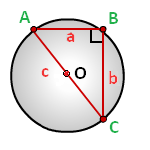
a, b – катеты прямоугольного треугольника
c – гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
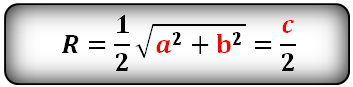
Калькулятор – вычислить, найти радиус описанной окружности прямоугольного треугольника
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 13 августа 2021
Радиус описанной окружности прямоугольного треугольника
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
a , b – катеты прямоугольного треугольника
c – гипотенуза
Формула радиуса описанной окружности прямоугольного треугольника (R):
Калькулятор – вычислить, найти радиус описанной окружности прямоугольного треугольника
Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:


где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:


где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
Радиус описанной окружности около прямоугольного треугольника онлайн
С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.

На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:
( small R=frac<large c> <large 2 sin C>)
где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:
( small R=frac<large c><large 2 sin 90°>=frac<large c><large 2>, )
| ( small R=frac<large c><large 2>. ) | (1) |
Пример 1. Известна гипотенуза ( small с=frac<9> <2>) прямоугольного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (1).
Подставим значение ( small c=frac<9> <2>) в (1):

Ответ: 
2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника. Найдем радиус описанной окружности около треугольника (Рис.2).

Из теоремы Пифагора запишем формулу гипотенузы, выраженная через катеты:
| ( small c=sqrt. ) | (2) |
Подставляя (2) в (1), получим:
| ( small R=frac<large sqrt><large 2>. ) | (3) |
Пример 2. Катеты прямоугольного треугольника равны: ( small a=15 , ; b=3.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения ( small a=15 , ; b=3) в (3):

Ответ: 
3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника

Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):
 |
(4) |
4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис.4). Найдем радиус описанной окружности около треугольника.

Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:
( small angle A+angle B=90°. )
| ( small angle A=90°-angle B. ) | (5) |
Подставляя (5) в (4), получим:
( small R=frac<large a><large 2 sin A>=frac<large a><large 2 sin(90°-B)>) ( small =frac<large a> <large 2 cos B>)
| ( small R=frac<large a><large 2 cos B>. ) | (6) |
Пример 3. Катет прямоугольного треугольника равен: ( small a=15 ,) а прилежащий угол равен ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6). Подставим значения ( small a=15 , ; angle B=25° ) в (6):

Ответ: 
[spoiler title=”источники:”]
http://matworld.ru/geometry/radius-opisannoj-okruzhnosti-pryamougolnogo-treugolnika.php
[/spoiler]
Радиус описанной окружности прямоугольного треугольника, формула
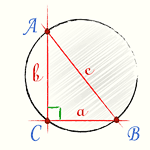
Если хорошенько приглядеться и построить еще один прямоугольный треугольник, равный первому и симметричный относительно гипотенузы, то мы увидим, что получился прямоугольник. Центр описанной окружности лежит на пересечении диагоналей этого прямоугольника. Отсюда следует, что гипотенуза прямоугольного треугольника является диаметром окружности. Соотвественно радиус описанной окружности прямоугольного треугольника вычисляется по формуле Пифагора:
[ R = frac{1}{2} sqrt{a^2+b^2}]
(a, b – стороны прямоугольного треугольника; R – радиус описанной окружности прямоугольного треугольника)
Вычислить, найти радиус описанной окружности прямоугольного треугольника по формуле (1)
Радиус описанной окружности прямоугольного треугольника |
стр. 247 |
|---|
Радиус описанной окружности около прямоугольного треугольника онлайн
С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
- Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
- Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
- Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.
На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:
где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:
то есть
Пример 1. Известна гипотенуза ( small с=frac{9}{2} ) прямоугольного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (1).
Подставим значение ( small c=frac{9}{2} ) в (1):
Ответ: 
2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника. Найдем радиус описанной окружности около треугольника (Рис.2).
Из теоремы Пифагора запишем формулу гипотенузы, выраженная через катеты:
Подставляя (2) в (1), получим:
или
Пример 2. Катеты прямоугольного треугольника равны: ( small a=15 , ; b=3.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения ( small a=15 , ; b=3) в (3):
Ответ: 
3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):
4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис.4). Найдем радиус описанной окружности около треугольника.
Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:
Откуда:
Подставляя (5) в (4), получим:
или
Пример 3. Катет прямоугольного треугольника равен: ( small a=15 ,) а прилежащий угол равен ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6). Подставим значения ( small a=15 , ; angle B=25° ) в (6):
Ответ: 
Смотрите также:
- Радиус описанной окружности около треугольника онлайн
- Радиус описанной окружности около равностороннего треугольника онлайн
- Радиус описанной окружности около равнобедренного треугольника онлайн
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
-
Формулы вычисления радиуса описанной окружности
-
Произвольный треугольник
- Прямоугольный треугольник
- Равносторонний треугольник
-
Произвольный треугольник
- Примеры задач
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
![]()

где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:


где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
![]()
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
![]()
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
![]()
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
