Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
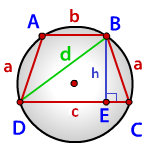
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
или
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров

Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD

I вариант нахождения радиуса для этого случая не изменяется.

Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
Свойства окружности, описанной вокруг трапеции
Содержание:
- Окружность, описанная около трапеции
-
Как найти радиус описанной окружности
- Если известны угол и диагональ трапеции
- Если известны диагональ, стороны трапеции и площадь одного из треугольников
- Если известны длины сторон треугольника
-
Как найти центр описанной окружности
- Если угол прямой
- Если угол острый
- Если угол тупой
- Задачи с решениями
Окружность, описанная около трапеции
Трапеция — это выпуклый четырехугольник, две стороны которого параллельны, а две другие — не параллельны.
Около четырехугольника можно описать окружность, если сумма его противолежащих углов равна 180°. Поэтому окружность можно описать только вокруг равнобедренной трапеции.
Как найти радиус описанной окружности
Самый распространенный способ найти радиус окружности, описанной около трапеции — через радиус окружности, описанной около треугольника, имеющего 3 любые общие вершины с данной трапецией.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Каждая диагональ делит трапецию на два треугольника. Описанная окружность проходит через все вершины трапеции, значит она проходит через все вершины каждого из этих треугольников и также является для них описанной окружностью.
Если известны угол и диагональ трапеции
Формула 1
(R=frac а{2cdotsinalpha},)
где R — радиус описанной окружности,
а — сторона треугольника,
α — угол треугольника, противолежащий стороне а.
Например, если известна диагональ BD=а и острый угол трапеции ABCD ∠CDA=β, то можем найти радиус описанной окружности.
Рассмотрим треугольник BCD. Сторона BD известна. (∠BCD=180°-∠CDA=180°-β).
Радиус описанной окружности будет равен (frac а{2cdotsinleft(180^circ-betaright)}).
Если известны диагональ, стороны трапеции и площадь одного из треугольников
Формула 2
(R=frac{abc}{4S}),
где R — радиус описанной окружности,
а, b, c — стороны треугольника,
S — площадь треугольника.
Если известны длины сторон треугольника
Формула 3
(R=frac{abc}{4sqrt{pleft(p-aright)left(p-bright)left(p-cright)}},)
где R — радиус описанной окружности,
а, b, c — стороны треугольника,
p — ½ периметра треугольника.
Как найти центр описанной окружности
Центр описанной окружности может лежать как внутри трапеции, так и вне ее. Определить его местонахождение помогает угол между диагональю трапеции и боковой стороной.
Если угол прямой
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр описанной окружности будет лежать на середине большего основания. Тогда большее основание будет равно диаметру описанной окружности.
Формула 4
(R=frac12а,)
где R — радиус описанной окружности,
а — большее основание трапеции.
Если угол острый
Если диагональ трапеции и боковая сторона образуют острый угол, то центр описанной около трапеции окружности лежит внутри трапеции.
Если угол тупой
Если диагональ трапеции и боковая сторона образуют тупой угол, то центр описанной около трапеции окружности будет лежать вне трапеции за ее большим основанием.
Задачи с решениями
Задача
Дано: трапеция с описанной окружностью. Периметр трапеции равен 22 см, а ее средняя линия — 5 см.
Найти: боковую сторону трапеции.
Решение: Так как около трапеции описана окружность, эта трапеция — равнобедренная. Удвоенная средняя линия трапеции равна сумме ее оснований (10 см). Сумма двух боковых сторон равна 22-10=12 (см). Боковая сторона трапеции равна 6 см.
Ответ: 6 см.
Примечание
Дано: основания трапеции ВС=11 см и AD=21 см. Диагональ трапеции ВD=20 см.
Найти: радиус описанной окружности.
Решение: найдем радиус окружности, описанной около (ΔABD. R=frac{BD}{2sinangle A}.)
- Трапеция ABCD равнобедренная, AB=CD, так как описать окружность можно только около равнобедренной трапеции.
- ВЕ — высота трапеции. Отрезок (АЕ=(21-11):2=5 (см)) по свойству равнобедренной трапеции. Отрезок ЕD=21-5=16 (см).
- Треугольник BED прямоугольный. ∠BED=90°. По теореме Пифагора (BE=sqrt{20^2-16^2}=12 (см).)
- Треугольник АBE также прямоугольный. ∠BED=90°. По теореме Пифагора (АВ=sqrt{5^2+12^2}=13 (см).)
- (sin∠BAD=frac{12}{13}) по определению синуса.
- (R=frac{BD}{2sinangle A}=10frac56 (см).)
Ответ: (10frac56 см.)
Радиус описанной окружности равнобокой трапеции
a – боковые стороны трапеции
c – нижнее основание
b – верхнее основание
d – диагональ
p – полупериметр треугольника DBC
p = (a+d+c)/2
Формула радиуса описанной окружности равнобокой трапеции, (R)
Калькулятор – вычислить, найти радиус описанной окружности трапеции
- Подробности
-
Автор: Administrator
-
Опубликовано: 11 сентября 2011
-
Обновлено: 13 августа 2021
Радиус описанной окружности равнобокой трапеции
a – боковые стороны трапеции
c – нижнее основание
b – верхнее основание
d – диагональ
p – полупериметр треугольника DBC
p = ( a + d + c )/2
Формула радиуса описанной окружности равнобокой трапеции, (R)
Калькулятор – вычислить, найти радиус описанной окружности трапеции
Радиус описанной окружности трапеции
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
где синус угла A можно найти из прямоугольного треугольника ABF:
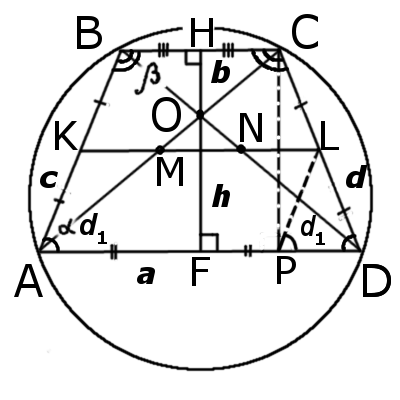
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
I вариант нахождения радиуса для этого случая не изменяется.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
Окружность описанная около равнобедренной трапеции формула
Радиус описанной окружности равнобокой трапеции
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
p — полупериметр треугольника DBC
p = ( a + d + c )/2
Формула радиуса описанной окружности равнобокой трапеции, (R)
Калькулятор — вычислить, найти радиус описанной окружности трапеции
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
 |
| Рис.1 |
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a — 2 h ctg α = a — 2 c cos α
| c = | h | = | a — b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 — c 2 | b = | d 1 2 — c 2 | c = √ d 1 2 — ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | — b b = | 2S | — a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
m = a — h ctg α = b + h ctg α = a — √ c 2 — h 2 = b + √ c 2 — h 2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 — ( a — b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a — b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
d 1 = √ a 2 + c 2 — 2 ac cos α
d 1 = √ b 2 + c 2 — 2 bc cos β
4. Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √ 4 c 2 — ( a — b ) 2 |
| 4 |
2. Формула площади через стороны и угол:
S = ( b + c cos α ) c sin α = ( a — c cos α ) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
a — большее основание
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Радиус описанной окружности трапеции
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
I вариант нахождения радиуса для этого случая не изменяется.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/okruzhnost-opisannaya-okolo-ravnobedrennoy-trapetsii-formula
[/spoiler]
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.{1}^{○}$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям – подобны.
$$ 4.{2}^{○}$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.{3}^{○}$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.{4}^{○}$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.{5}^{○}$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.{6}^{○}$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.{7}^{○}$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.{8}^{○}$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
$$ 4.{9}^{○}$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` – диагональ, `c` – боковая сторона, `a` и `b` основания.
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.{10}^{○}$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.{11}^{○}$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Докажем, например, утверждение $$ 4.{9}^{○}$$.
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Складывая, получаем
`d_1^2+d_2^2=a^2+b^2+c_2^2+(c_2^2-2(a-b)c_2cosvarphi)`. (2)
Проводим `CK“||“BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
`d_1^2+d_2^2=a^2+b^2+c_2^2+(c_1^2-(a-b)^2)=`
`=(a^2+b^2+c_2^2)+(c_1^2-a^2-b^2+2ab)`.
Окончательно имеем
`d_1^2+d_2^2=c_1^2+c_2^2+2ab`.
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
.
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.{2}^{○}$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` – его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` – её точка пересечения с прямой `BC` (рис. 30б).
По построению `ACKD` – параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`
(т. к. угол `BDK` – это угол между диагоналями трапеции).
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
`S_(BDK)=1/2BK*DP=1/2(BC+AD)DP=S_(ABCD)`.
Итак, `S_(ABCD)=S=24`.
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Пусть `BC=a`, `AD=b`, и пусть `h` – высота трапеции (рис. 31). По свойству $$ 4.{1}^{○}$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
`S_1+S_2+2S_0=(sqrt(S_1)+sqrt(S_2))^2`.
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Трапеция равнобокая, по свойству $$ 4.{11}^{○}$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.{6}^{○}$$
`AK=(AD-BC)/2=1`, `KD=(AD+BC)/2=9`.
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
`R=(3sqrt(10))/(2*3//sqrt(10)) =5`.
$$ 4.{12}^{○}$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
$$ 4.{13}^{○}$$. Если `S_1` и `S_2` – площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.
$$ 4.{14}^{○}$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` – какая-то сторона (или диагональ трапеции), `alpha` – смотрящий на неё вписанный угол.