1) Если вам известны объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3∙πR²H. Получите: R²=3V/πH, откуда R=√ (3V/πH)
. 2) Если вам известны площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=πRL. Вы получите R=S/πL.
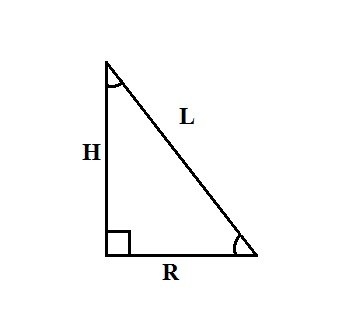
3) Следующие способы нахождения радиуса основания конуса базируются на утверждении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам известны высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L²=R²+H². Выразите из данной формулы R, получите: R²=L²-H² и R=√ (L²-H²).
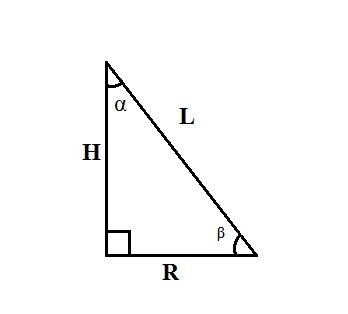
4) Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если известны образующая конуса L и угол α между высотой конуса и его образующей, найдите радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L∙sinα.
5) Если известны образующая конуса L и угол β между радиусом основания конуса и его образующей, найдите радиус основания R по формуле: R=L∙cosβ. Если известны высота конуса H и угол α между его образующей и радиусом основания, найдите радиус основания R по формуле: R=H∙tgα.
6) Пример: образующая конуса L равна 20 см и угол α между образующей и высотой конуса равен 15º. Найдите радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом α противолежащий этому углу катет R вычисляется по формуле R=L∙sinα. Подставьте соответствующие значения, получите: R=L∙sinα=20∙sin15º. Sin15º находится из формул тригонометрических функций половинного аргумента и равен 0,5√ (2-√3). Отсюда катет R=20∙0,5√ (2-√3) = 10√ (2-√3) см. Соответственно, радиус основания конуса R равен 10√ (2-√3) см.
7) Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30º, равен половине гипотенузы. Таким образом, если известны длина образующей конуса и угол между его образующей и высотой равен 30º, то найдите радиус по формуле: R=1/2L.
ДЗ
Знаток
(319),
закрыт
9 лет назад
Дополнен 11 лет назад
Например
r=20см/2
h=21см/2
Лучший ответ
Ру Медведкин
Профи
(646)
11 лет назад
Высота, радиус и образующая образуют прямоугольный треугольник. Теорема Пифагора.
Образующая в квадрате минус высота в квадрате равняется радиус в квадрате. Извлекаешь корень. Задача решена.
Источник: голова
Остальные ответы
Любовь Юдаева
Мастер
(1781)
11 лет назад
По теореме Пифагора, из квадрата образующей вычесть квадрат высоты, получим квадрат радиуса.
Похожие вопросы
1)Если вам известны объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3∙πR²H. Получите: R²=3V/πH, откуда R=√(3V/πH)
.2)Если вам известны площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=πRL. Вы получите R=S/πL.
3)Следующие способы нахождения радиуса основания конуса базируются на утверждении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам известны высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L²=R²+H². Выразите из данной формулы R, получите: R²=L²–H² и R=√(L²–H²).
4)Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если известны образующая конуса L и угол α между высотой конуса и его образующей, найдите радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L∙sinα.
5)Если известны образующая конуса L и угол β между радиусом основания конуса и его образующей, найдите радиус основания R по формуле: R=L∙cosβ. Если известны высота конуса H и угол α между его образующей и радиусом основания, найдите радиус основания R по формуле: R=H∙tgα.
6)Пример: образующая конуса L равна 20 см и угол α между образующей и высотой конуса равен 15º. Найдите радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом α противолежащий этому углу катет R вычисляется по формуле R=L∙sinα. Подставьте соответствующие значения, получите: R=L∙sinα=20∙sin15º. Sin15º находится из формул тригонометрических функций половинного аргумента и равен 0,5√(2–√3). Отсюда катет R=20∙0,5√(2–√3)=10√(2–√3)см. Соответственно, радиус основания конуса R равен 10√(2–√3)см.
7)Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30º, равен половине гипотенузы. Таким образом, если известны длина образующей конуса и угол между его образующей и высотой равен 30º, то найдите радиус по формуле: R=1/2L.
Как обнаружить радиус основания конуса
Прямой конус – это тело, которое получается при вращении прямоугольного треугольника вокруг одного из катетов. Данный катет есть высота конуса H, иной катет является радиусом его основания R, гипотенуза равна множеству образующих конуса L. Метод нахождения радиуса конуса зависит от начальных данных задачи.
Инструкция
1. Если вам знамениты объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3??R?H. Получите: R?=3V/?H, откуда R=?(3V/?H).
2. Если вам вестимы площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=?RL. Вы получите R=S/?L.
3. Следующие методы нахождения радиуса основания конуса основываются на заявлении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам вестимы высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L?=R?+H?. Выразите из данной формулы R, получите: R?=L?–H? и R=?(L?–H?).
4. Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если знамениты образующая конуса L и угол ? между высотой конуса и его образующей, обнаружьте радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L?sin?.
5. Если знамениты образующая конуса L и угол ? между радиусом основания конуса и его образующей, обнаружьте радиус основания R по формуле: R=L?cos?. Если знамениты высота конуса H и угол ? между его образующей и радиусом основания, обнаружьте радиус основания R по формуле: R=H?tg?.
6. Пример: образующая конуса L равна 20 см и угол ? между образующей и высотой конуса равен 15?. Обнаружьте радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом ? противолежащий этому углу катет R вычисляется по формуле R=L?sin?. Подставьте соответствующие значения, получите: R=L?sin?=20?sin15?. Sin15? находится из формул тригонометрических функций половинного довода и равен 0,5?(2–?3). Отсель катет R=20?0,5?(2–?3)=10?(2–?3)см. Соответственно, радиус основания конуса R равен 10?(2–?3)см.
7. Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30?, равен половине гипотенузы. Таким образом, если знамениты длина образующей конуса и угол между его образующей и высотой равен 30?, то обнаружьте радиус по формуле: R=1/2L.
Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π.
d=2r
P=2πr
S_(осн.)=πr^2
Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2)
h=√(l^2-r^2 )
cosβ=r/l
α=180°-2β
Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса.
S_(б.п.)=πrl
S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)
Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту.
V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4)
r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r)
R=l^2/2h