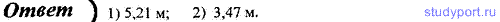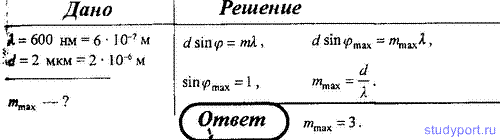Основные формулы
Радиус внешней границы m-й зоны Френеля для сферической волны.
где m – номер зоны Френеля; λ – длина волны,
a и b – соответственно расстояния диафрагмы с круглым отверстием от точечного источника и от экрана, на котором дифракционная картина наблюдается.
Условия дифракционных максимумов и минимумов от одной щели, на которую свет падает нормально:
|
asinϕ = ±(2m +1) |
λ |
, |
(2) |
|
2 |
|||
|
asinϕ = ±2m λ , |
(3) |
||
|
2 |
|||
|
(m = 1,2,3, …), |
где a – ширина щели; ϕ – угол дифракции; m – порядок спектра; λ – длина волны.
Условия главных максимумов и дополнительных минимумов дифракционной решётки , на которую свет падает нормально:
|
dsinϕ = ±2m |
λ |
, (m = 0,1,2, …); |
(4) |
|||
|
2 |
||||||
|
dsinϕ = ±m′ |
λ |
( m′ = 1,2,3, …, кроме 0, N, 2N, …), |
(5) |
|||
|
N |
||||||
|
где d – период дифракционной решётки; |
||||||
|
N – число штрихов решётки. |
||||||
|
Период дифракционной решётки: |
||||||
|
d = |
1 |
, |
(7) |
|||
|
N0 |
||||||
|
где N0 – число щелей , приходящихся на единицу длины решётки. |
||||||
|
Условие дифракционных максимумов от пространственной решётки (формула Вульфа- |
||||||
|
Брэггов): |
||||||
|
2dsinθ = mλ (m = 1,2,3, …), |
(8) |
где d – расстояние между атомными плоскостями кристалла; θ – угол скольжения.
Наименьшие угловое расстояние между двумя светлыми точками, при котором изображения этих точек могут быть разрешены в фокальной плоскости объектива:
11
где D – диаметр объектива; λ – длина волны света.
Разрешающая способность дифракционной решётки:
|
R = |
λ |
= mN, |
(10) |
|
|
δλ |
||||
где λ, (λ + δλ) – длины волн двух соседних спектральных линий, разрешаемых решеткой;
m – порядок спектра;
N – общие число штрихов решётки.
Примеры решения задач
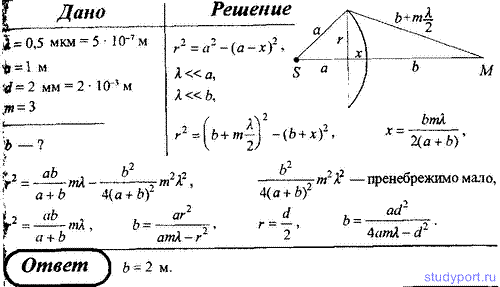
Пример №1. Точечный источник света (L=0,5 мкм) расположен на расстоянии а=1 м перед диафрагмой с круглым отверстием диаметра d=2 мм. Определите расстояние b от диафрагмы до точки наблюдения, если отверстие открывает 3 зоны Френеля.
Дано:
λ = 0,5 мкм =5 10−7 м a=1м
d=2мм= 2 10−3 м m=3
b-?
Решение:
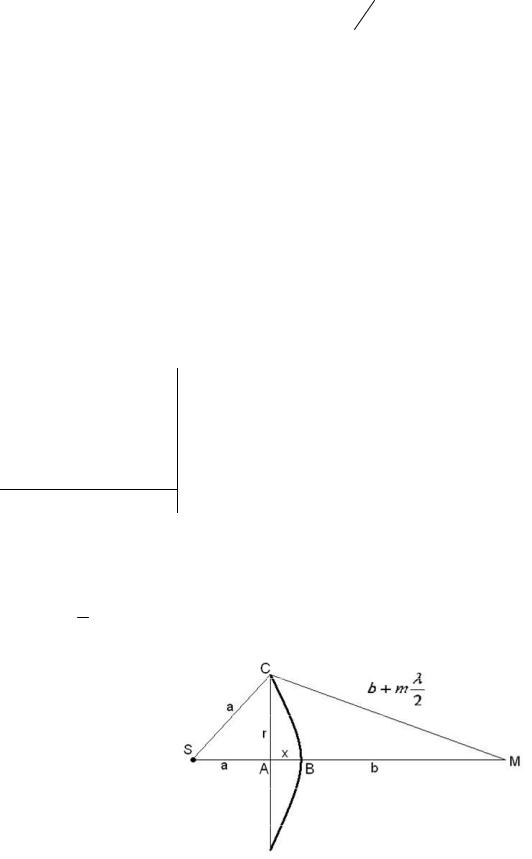
Рассмотрим треугольник SCA, его сторону AC можно легко найти по теореме Пифагора, она же является радиусом отверстия:
r2 = a 2 − (a − x)2 ,
r – радиус отверстия, a – расстояние между диафрагмой и отверстием, x – высота сферического сегмента.
С другой стороны, AC можно найти из треугольника ACM:
|
r |
2 |
λ |
2 |
2 |
, |
|
|
= b + m |
− (b + x) |
|||||
|
2 |
b + m λ2 – расстояние от зоны Френеля до точки M.
Учитывая, что
λ<<a, λ – длина волны, a – расстояние от источника света до отверстия,
λ<< b, b – расстояние от отверстия до точки наблюдения.
Можно выразить высоту сферического элемента
12

x = bmλ , 2(a + b)
|
r2 = |
ab |
mλ − |
b2 |
m2 λ2 , |
||||||||
|
a + b |
4(a + b)2 |
|||||||||||
|
b2 |
m2 λ2 |
т.к. отверстие мало, то можно считать высоту сферического сегмента пре- |
||||||||||
|
4(a + b)2 |
||||||||||||
|
небрежительно малой величиной, тогда квадрат радиусы отверстия равен |
||||||||||||
|
r2 = |
ab |
mλ выразим расстояние до точки наблюдения, получаем b = |
ar2 |
, |
||||||||
|
a + b |
amλ − r2 |
|||||||||||
|
подставив в формулу диаметр получаем |
||||||||||||
|
b = |
ad2 |
, |
||||||||||
|
4amλ − d2 |
||||||||||||
|
b = |
1м (2 10−3 м)2 |
|
4 1м 5 10−7 м − (2 10−3 м)2 =2 м. |
Ответ: b=2 м.
Пример №2. Определите радиус третьей зоны Френеля для случая плоской волны. Расстояние от волновой поверхности до точки наблюдения равно 1,5 м. Длина волны λ =0,6 мкм.
|
Дано: |
Решение: |
||||||
|
m=3 |
Расстояние от зоны Френеля до точки наблюдения M, можно найти |
||||||
|
b=1,5 м |
как гипотенузу треугольника AOM, где O – центр отверстия. |
||||||
|
λ =0,6 мкм = 6 10−7 м |
2 |
2 |
λ 2 |
||||
|
r |
+ b |
= b + m |
, |
||||
|
r – ? |
|||||||
|
2 |
где λ– длина волны, m – номер зоны Френеля, r –расстояние от центра отверстия, до m-й зоны Френеля, b – расстояние от волновой поверхности до точки наблюдения.
Выразим радиус зоны Френеля
r2 = bmλ + m2 λ2 . 4
λ << b Длина волны значительно меньше расстояние пройденного ей – необходимое условие дифракции волн.
13
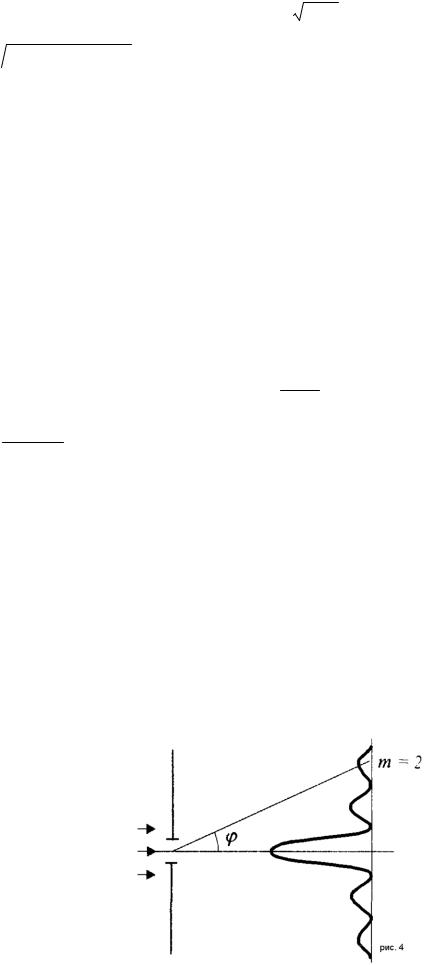
m2 λ2 пренебрежимо мало, следовательно r = bmλ 4
r = 
Ответ: r=1,64 мм.
Пример №3. Зонная пластинка даёт изображение источника, удалённого от неё на 2 метра, на расстоянии 1 метра от своей поверхности. Где получится изображение источника, если его удалить в бесконечность?
|
Дано: |
Решение: |
||||
|
a = 2 м |
Воспользуемся формулой из примера 1: |
||||
|
b = 1 м |
r2 |
= |
ab |
mλ. |
|
|
a1 =∞ |
a + b |
||||
|
m |
|||||
|
Воспользуемся формулой из примера 2: |
|||||
|
b1 −? |
|||||
|
r2 |
= mb |
λ. |
|||
|
m |
1 |
Приравняем и выразим b1
b1 = aab+ b ,
b1 =11мм+22мм =66,7 см.
Ответ: b1 =66,7 см.
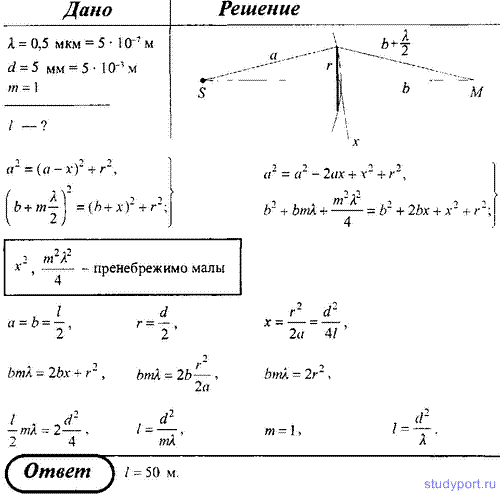
Пример №4. На узкую щель шириной a = 0,05 м падает нормально монохроматический свет длиной волны λ = 694 нм. Определите направление света на вторую дифракционную полосу (по отношению к первоначальному направлению света).
|
Дано: |
Решение: |
||||
|
a = 0,05 |
м = 5 10−5 м |
Запишем условие дифракционных минимумов. |
|||
|
λ = 694 |
нм = 6,94 10−7 м |
a sinφ = ±(2m +1) |
λ |
||
|
m = 2 |
2 , |
||||
|
где a – ширина щели, λ – длина волны, φ – угол, под которым падает |
|||||
|
φ – ? |
|||||
|
свет, m – номер дифракционного максимума. |
|||||
14
Выразим синус угла:
sinφ = (2m +1)λ , 2a
= 5 6,94 10−7 м
sinφ 2 5 10−5 м =0,0347,
φ= arcsin φ=2º.
Ответ: φ=2º.
Пример №5. На узкую щель падает нормально монохроматический свет. Его направление на четвёртую тёмную дифракционную полосу составляет 2º12´. Определите, сколько длин волн укладываются на ширину щели.
|
Дано: |
Решение: |
|||||||
|
φ = 2º12´ |
Запишем формулу для максимумов дифракционной решётки |
|||||||
|
m = 4 |
a sinφ = ±mλ, (m=4). |
|||||||
|
a |
||||||||
|
a |
– ? |
Выразим |
: |
|||||
|
λ |
λ |
|||||||
|
a |
= |
m |
, гдеφ= 2º12´=2,2º; |
|||||
|
λ |
sinφ |
|||||||
aλ = sin2,24 ° =104.
Ответ: aλ = 104.
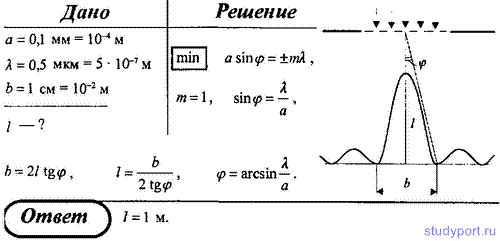
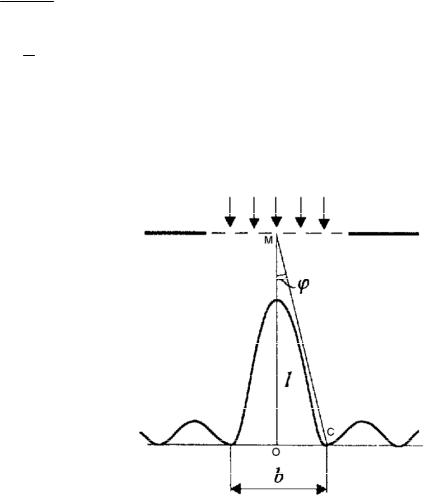
Пример №6. На щель шириной a = 0,1 мм падает нормально монохроматический свет длиной волны λ = 0,5 мкм. Дифракционная картина наблюдается на экране, расположенном параллельно щели. Определите расстояние l от щели до экрана, если ширина центрального дифракционного максимума b = 1 см.
15
|
Дано: |
Решение: |
||||||||||
|
a = 0,1 мм = 10−4 м |
Запишем формулу для минимумов дифракционной решётки |
||||||||||
|
λ = 0,5 мкм = 5 10−7 м |
λ |
||||||||||
|
b =1 см = 10−2 м |
следовательно |
a sinφ = ±mλ, где m=1, sinφ = a |
, |
||||||||
|
l – ? |
|||||||||||
|
ϕ = arcsin |
λ |
=arcsin |
5 10−7 |
=0,286, |
|||||||
|
a |
10−4 |
||||||||||
|
∆MOC прямоугольный, значит можно найти b |
|||||||||||
|
b= 2 l tgφ, следовательно |
|||||||||||
|
b |
|||||||||||
|
l= |
, |
||||||||||
|
2 tgφ |
|||||||||||
|
l= |
10−2 м |
=1м. |
|||||||||
|
2 |
tg0,286 |
||||||||||
Ответ: l = 1 м.
Пример №7. На дифракционную решётку нормально падает монохроматический свет длиной волны λ =600 нм. Определить наибольший порядок спектра, полученного с помощью этой решётки, если её постоянная d = 2 мкм.
|
Дано: |
Решение: |
|||
|
λ =600 нм = 6 10−7 м |
Запишем формулу максимумов дифракционной решётки |
|||
|
d = 2 мкм = 2 10 |
−6 |
м |
dsinφ = mλ, |
|
|
где d – период дифракционной решётки |
||||
|
mmax −? |
||||
|
m наибольшие будет |
при наибольшем значении sinφ. |
|||
Синус принимает значения: −1 ≤sinϕ ≤1, наибольшие значение 1. sinφmax =1
Порядок спектра примет вид:
|
m |
= |
d |
= |
2 10−6 |
=3,33. |
||
|
max |
λ |
6 10−7 |
|||||
Порядок спектра может принимать только целые значения, поэтому mmax =3.
Ответ: mmax =3.
Пример №8. На дифракционную решётку длиной l=15 мм, содержащую N= 3000 штрихов, падает нормально монохроматический свет длиной волны λ = 550 нм. Определите 1) Число максимумов, наблюдаемых в спектре дифракционной решётки. 2). Угол, соответствующий последнему максимуму.
16

|
Дано: |
Решение: |
||||||
|
l= 15 мм=1.5 10−2 м |
Запишем формулу максимумов дифракционной решётки |
||||||
|
N= с |
dsinφ = ±mλ (m=0,1,2,….), |
||||||
|
λ = 550 нм= 5,5 10−7 м |
d = |
l |
– период дифракционной решётки, |
||||
|
1)n -? |
N |
||||||
|
2) φmax − ? |
N – число штрихов |
||||||
|
m |
max |
= |
d |
, когда sin φ =1, |
|||
|
λ |
Подставим период дифракционной решётки
mmax = N1λ .
Общие число максимумов в 2 раза больше числа порядков т.к. максимумы располагаются по обе стороны от центра дифракционной картины.
|
n = 2m |
= |
2l |
= |
2 1.5 10−2 |
=18 |
||
|
max |
Nλ |
3000 5,5 10−7 |
|||||
Запишем формулу наибольшего максимума dsinφmax = mλmax , следовательно
sinφmax = mmaxd λ = mmaxl λN ,
Найдём угол φmax = arcsin mmax λN l
|
φmax |
= arcsin |
9 5,5 10−7 м 3000 |
=81º54´. |
|
|
1.5 10−2 м |
||||
Ответ: 1) n=18; 2) φmax =81º54´.
Пример №9. Определите число штрихов на 1 мм дифракционной решётки, если углу φ=30º
соответствует максимум 4-го порядка для монохроматического света с длиной волны
λ = 0,5 мкм.
|
Дано: |
Решение: |
||||
|
φ=30º |
Запишем формулу максимума дифракционной решётки |
||||
|
m=4 |
dsinφ = ±mλ, |
||||
|
λ = 0,5 мкм = 5 10−7 м |
где m = 4 (порядок спектра). |
||||
|
Выразим период решётки: |
|||||
|
n-? |
|||||
|
d= |
mλ |
, |
|||
|
sinφ |
|||||
|
с другой стороны |
|||||
|
d = |
1 |
. |
|||
|
N |
Число штрихов на 1 мм равно общему числу штрихов, на длину дифракционной решётки.
17
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема: Дифракция от круглого отверстия (Прочитано 27601 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Fiz
Точечный источник света с длиной волны 0,5 мкм расположен на расстоянии 1 м перед диафрагмой с круглым отверстием радиусом 1 мм. Найти расстояние от диафрагмы до точки наблюдения, находящейся на оси отверстия, для которой число зон Френеля в отверстии равно 3.
Темное или светлое пятно получится в центре дифракционной картины, если в месте наблюдения поместить экран?
« Последнее редактирование: 31 Марта 2011, 09:17 от alsak »
Записан
Скачиваем и читаем книгу
Мякишев Г.Я. Физика: Оптика. Квантовая физика. 11 кл.: Учеб. для углубленного изучения физики. — М.: Дрофа, 2002. — 464 с.
О зонах Френеля см. на стр. 154-155.
Решение. Точечный источник будет создавать сферическую волну. Радиус m зоны Френеля для сферической волны равен
[ r_{m} = sqrt{frac{a cdot b}{a+b} cdot m cdot lambda}, ]
где rm = 1 мм, a = 1 м — расстояние от источника света до диафрагмы, b — это расстояние от диафрагмы до точки наблюдения (его надо найти), m = 3 — число зон, λ = 0,5 мкм — длина волны. Тогда
[ r_{m}^{2} = frac{a cdot b}{a+b} cdot m cdot lambda, ; ; ; r_{m}^{2} cdot a + r_{m}^{2} cdot b = a cdot b cdot m cdot lambda, ]
[ b = frac{r_{m}^{2} cdot a}{a cdot m cdot lambda – r_{m}^{2}}, ]
b = 2 м.
При дифракции на круглом отверстии, если число открытых зон Френеля нечетное (m = 3), то в центре дифракционной картины будет наблюдаться максимум, т.е. светлое пятно.
О дифракции на круглом отверстии см. стр. 159-160.
Записан
Fiz
Записан
Fiz
А вот Вы можете рисуночек к задаче показать, мне очень нужно?
А есть другие способы решения этой задачи?
Если они есть, то расскажите о них?
« Последнее редактирование: 03 Апреля 2011, 17:46 от Fiz »
Записан
Все рисуночки вы можете посмотреть в книге, которую я вам указал.
Записан
Fiz
И всё таки как нарисовать диафрагму с круглым отверстием
У меня получилось вот что
Записан
См. рис. 2.26 на стр. 159.
Записан
Fiz
А где на нём сферическая волна показана?
Там только две зоны Френеля, а надо три, помогите пожалуйста нарисовать.
Спасибо!
« Последнее редактирование: 03 Апреля 2011, 23:41 от Fiz »
Записан
А где на нём сферическая волна показана?
Вы внимательно читали страницы, которые я вам указал еще в первом сообщении? Например,
О зонах Френеля см. на стр. 154-155.
Где вы видели там на рисунках сферу, которую рисовали бы полностью? Рисуется часть сферы дуга M1M2 (см. рис. 2.21, 2.23, 2.26).
Там только две зоны Френеля, а надо три, помогите пожалуйста нарисовать.
Во-первых, если бы в условии было сказано 10 зон – вы бы и рисовали 10 зон? А если 100? Рисунки всегда рисуются схематически, для общих случаев.
Во-вторых, если вы уже захотели нарисовать три зоны, и сообразили, что там нарисовано только две, то вы не в состоянии нарисовать еще одну прямую линию (сдвинув BM1 немного вниз)?
Записан
Fiz
Я не понимаю как надо рисовать.Помогите пожалуйста.
Записан
Страница 1 из 3
68. Точечный источник света (λ = 0,5 мкм) расположен на расстоянии a = 1 м перед диафрагмой с круглым отверстием диаметра d = 2 мм. Определите расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля.
69. Определите радиус третьей зоны Френеля, если расстояние от точечного источника света (λ = 0,6 мкм) до волновой поверхности и от волновой поверхности до точки наблюдения равно 1,5 м.
70. На диафрагму с круглым отверстием диаметром d = 5 мм падает нормально параллельный пучок света с длиной волны λ = 0,6 мкм. Определите расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля.
71. Определите радиус третьей зоны Френеля для случая плоской волны. Расстояние от волновой поверхности до точки наблюдения равно 1,5 м. Длина волны λ = 0,6 мкм.
72. Определите радиус четвертой зоны Френеля, если радиус второй зоны Френеля для плоского волнового фронта равен 2 мм.
73. Определите радиус первой зоны Френеля, если расстояние от точечного источника света (λ = 0,5 мкм) до зонной пластинки и от пластинки до места наблюдения a = b = 1 м.
74. На зонную пластинку падает плоская монохроматическая волна (λ = 0,5 мкм). Определите радиус первой зоны Френеля, если расстояние от зонной пластинки до места наблюдения b = 1 м.
75. Зонная пластинка дает изображение источника, удаленного от нее на 2 м, на расстоянии 1 м от своей поверхности. Где получится изображение источника, если его удалить в бесконечность?
76. Дифракция наблюдается на расстоянии 1 м от точечного источника монохроматического света (λ = 0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определите радиус отверстия, при котором центр дифракционных колец на экране является наиболее темным.
77. Сферическая волна, распространяющаяся из точечного монохроматического источника света (λ = 0,6 мкм), встречает на своем пути экран с круглым отверстием радиусом r = 0,4 мм. Расстояние a от источника до экрана равно 1 м. Определите расстояние от отверстия до точки экрана, лежащей на линии, соединяющей источник с центром отверстия, где наблюдается максимум освещенности.
78. На экран с круглым отверстием радиусом r = 1,5 мм нормально падает параллельный пучок монохроматического света с длиной волны λ = 0,5 мкм. Точка наблюдения находится на оси отверстия на расстоянии b = 1,5 м от него. Определите: 1) число зон Френеля, укладывающихся в отверстии; 2) темное или светлое кольцо наблюдается в центре дифракционной картины, если в месте наблюдения помещен экран.
79. На экран с круглым отверстием радиусом r = 1,2 мм нормально падает параллельный пучок монохроматического света с длиной волны λ = 0,6 мкм. Определите максимальное расстояние от отверстия на его оси, где еще можно наблюдать наиболее темное пятно.
81. Дифракция наблюдается на расстоянии l от точечного источника монохроматического света (λ = 0,5 мкм). Посередине между источником света и экраном находится непрозрачный круглый диск диаметром 5 мм. Определите расстояние l, если диск закрывает только центральную зону Френеля.
82. На узкую щель шириной a = 0,05 мм падает нормально монохроматический свет с длиной волны λ = 694 нм. Определите направление света на вторую дифракционную полосу (по отношению к первоначальному направлению света).
83. На узкую щель падает нормально монохроматический свет. Его направление на четвертую темную дифракционную полосу составляет 2°12′. Определите, сколько длин волн укладывается на ширине щели.
84. На щель шириной a = 0,1 мм падает нормально монохроматический свет (λ = 0,6 мкм). Экран, на котором наблюдается дифракционная картина, расположен параллельно щели на расстоянии l = 1 м. Определите расстояние b между первыми дифракционными минимумами, расположенными по обе стороны центрального фраунгоферова максимума.
85. На щель шириной a = 0,1 мм падает нормально монохроматический свет с длиной волны λ = 0,5 мкм. Дифракционная картина наблюдается на экране, расположенном параллельно щели. Определите расстояние l от щели до экрана, если ширина центрального дифракционного максимума b = 1 см.
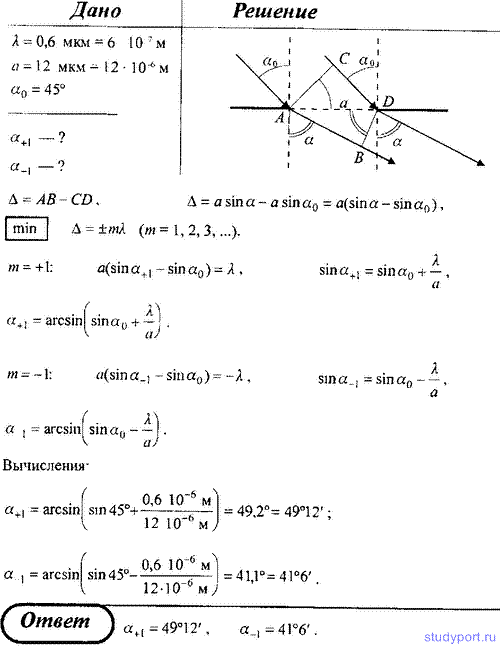
86. Монохроматический свет с длиной волны λ = 0,6 мкм падает на длинную прямоугольную щель шириной a = 12 мкм под углом α0 = 45° к ее нормали. Определите угловое положение первых минимумов, расположенных по обе стороны центрального фраунгоферова максимума.
87. Монохроматический свет падает на длинную прямоугольную щель шириной a = 12 мкм под углом α = 30° к ее нормали. Определите длину волны λ света, если направление φ на первый минимум (m = 1) от центрального фраунгоферова максимума составляет 33°.
88. На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 600 нм. Определите наибольший порядок спектра, полученный с помощью этой решетки, если ее постоянная d = 2 мкм.