Как найти радиус первой боровской орбиты - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 сентября 2022 года; проверки требуют 3 правки.

Боровская модель водородоподобного атома (Z — заряд ядра), где отрицательно заряженный электрон заключен в атомной оболочке, окружающей малое, положительно заряженное атомное ядро. Переход электрона с орбиты на орбиту сопровождается излучением или поглощением кванта электромагнитной энергии (hν).

Бо́ровская моде́ль а́тома (моде́ль Бо́ра, моде́ль Бо́ра — Резерфо́рда) — полуклассическая модель атома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Эрнестом Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать энергию непрерывно и очень быстро и, потеряв её, упасть на ядро. Чтобы преодолеть эту проблему, Бор ввёл допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определённым (стационарным) орбитам, находясь на которых они не излучают энергию, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причём, стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка^[1]: $m_{e}vr=nhbar$ .

Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты R_n и энергии $E_{n}$ находящегося на этой орбите электрона:

${displaystyle R_{n}=4pi {frac {varepsilon _{0}}{Ze^{2}}}{frac {n^{2}hbar ^{2}}{m_{e}}};quad E_{n}=-{frac {1}{8pi }}{frac {Ze^{2}}{varepsilon _{0}}}{frac {1}{R_{n}}};}$

Здесь m_e — масса электрона, — количество протонов в ядре, $varepsilon _{0}$ — электрическая постоянная, — заряд электрона.

Именно такое выражение для энергии можно получить, применяя уравнение Шрёдингера в задаче о движении электрона в центральном кулоновском поле.

Радиус первой орбиты в атоме водорода R₀=5,2917720859(36)⋅10⁻¹¹ м^[2], ныне называется боровским радиусом, либо атомной единицей длины и широко используется в современной физике. Энергия первой орбиты $E_{0}=-13.6$ эВ представляет собой энергию ионизации атома водорода.

Полуклассическая теория Бора[править | править код]

Основана на двух постулатах Бора:

Далее исходя из соображений классической физики о круговом движении электрона вокруг неподвижного ядра по стационарной орбите под действием кулоновской силы притяжения, Бором были получены выражения для радиусов стационарных орбит и энергии электрона на этих орбитах:

$r_{n}=an^{2},$

$a={frac {hbar ^{2}}{kme^{2}}}=5.3cdot 10^{{-11}}$

м — боровский радиус.

$E_{n}=-R_{y}{frac {1}{n^{2}}},$

$R_{y}={frac {mk^{2}e^{4}}{2hbar ^{2}}}$

— энергетическая постоянная Ридберга (численно равна 13,6 эВ).

Формула Зоммерфельда — Дирака[править | править код]

Движение электрона вокруг атомного ядра в рамках классической механики можно рассматривать как «линейный осциллятор», который характеризуется «адиабатичным инвариантом», представляющим собой площадь эллипса (в обобщённых координатах):

$oint {mathbf {p}}cdot ,{mathbf {dq}}={frac {W}{nu }}=J$

где — обобщённый импульс и координаты электрона, — энергия, — частота.
А квантовый постулат утверждает, что площадь замкнутой кривой в фазовой — плоскости за один период движения, равна целому числу, умноженному на постоянную Планка (Дебай, 1913 г.).
С точки зрения рассмотрения постоянной тонкой структуры наиболее интересным является движение релятивистского электрона в поле ядра атома, когда его масса зависит от скорости движения. В этом случае мы имеем два квантовых условия:

$J_{1}=nh$

, $J_{2}=kh$

где определяет главную полуось эллиптической орбиты электрона (), а — его фокальный параметр :

$a=a_{0}n^{2}$

, $q=a_{0}k^{2}$

В этом случае Зоммерфельд получил выражение для энергии в виде

$E=-{frac {RyZ^{2}}{n^{2}}}+epsilon (n,k)$

где — постоянная Ридберга, а — порядковый номер атома (для водорода Z=1 ).

Дополнительный член отражает более тонкие детали расщепления спектральных термов водородоподобных атомов, а их число определяется квантовым числом . Таким образом сами спектральные линии представляют собой системы более тонких линий, которые соответствуют переходам между уровнями высшего состояния ( $n=n_{1},k=1,2,...,n_{1}$ ) и низшего состояния ( $n=n_{2},k=1,2,...,n_{2}$ ). Это и есть т. н. тонкая структура спектральных линий. Зоммерфельд разработал теорию тонкой структуры для водородоподобных атомов (, $He^{{+}}$ , $Li^{{2+}}$ ), а Фаулер с Пашеном на примере спектра однократно ионизированного гелия $He^{{+}}$ установили полное соответствие теории с экспериментом.

Зоммерфельд (1916 г.) еще задолго до возникновения квантовой механики Шредингера получил феноменологичную формулу для водородных термов в виде:

$E+E_{0}=E_{0}left(1+{frac {alpha ^{2}Z^{2}}{left(n_{r}+{sqrt {n_{phi }^{2}-alpha ^{2}Z^{2}}}right)^{2}}}right)^{{-1/2}}$

где alpha — постоянная тонкой структуры, — порядковый номер атома, $E_{0}=mc^{2}$ — энергия покоя, $n_{r}$ — радиальное квантовое число, а $n_{phi }$ — азимутальное квантовое число. Позднее эту формулу получил Дирак, используя релятивистское уравнения Шрёдингера. Поэтому сейчас эта формула и носит имя Зоммерфельда — Дирака.

Появление тонкой структуры термов связано с прецессией электронов вокруг ядра атома. Поэтому появление тонкой структуры можно обнаружить по резонансному эффекту в области ультракоротких электромагнитных волн. В случае Z=1 (атом водорода) величина расщепления близка к

$E/happrox Ralpha ^{2}/n^{2}$

Поскольку длина электромагнитной волны равна

$lambda =c/nu =ch/E=cn^{2}/Ralpha ^{2}approx 0,17cm$

Поэтому для n=2 это будет почти 1 см.

Достоинства теории Бора[править | править код]

Объяснила дискретность энергетических состояний водородоподобных атомов.
Теория Бора подошла к объяснению внутриатомных процессов с принципиально новых позиций, стала первой полуквантовой теорией атома.
Эвристическое значение теории Бора состоит в смелом предположении о существовании стационарных состояний и скачкообразных переходов между ними. Эти положения позднее были распространены и на другие микросистемы.

Недостатки теории Бора[править | править код]

Не смогла объяснить интенсивность спектральных линий.
Справедлива только для водородоподобных атомов и не работает для атомов, следующих за ним в таблице Менделеева без экспериментальных данных (энергии ионизации или других).
Теория Бора логически противоречива: не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно — уравнение движения электрона — классическое, другое — уравнение квантования орбит — квантовое.

Теория Бора являлась недостаточно последовательной и общей. Поэтому она в дальнейшем была заменена современной квантовой механикой, основанной на более общих и непротиворечивых исходных положениях. Сейчас известно, что постулаты Бора являются следствиями более общих квантовых законов. Но правила квантования широко используются и в наши дни как приближённые соотношения: их точность часто бывает очень высокой.

Экспериментальное подтверждение теории Бора[править | править код]

В 1914 году Франк и Герц поставили опыт, косвенно подтверждающий теорию Бора: атомы разреженного газа обстреливались медленными электронами с последующим исследованием распределения электронов по абсолютным значениям скоростей до и после столкновения. При упругом ударе распределение не должно меняться, так как изменяется только направление вектора скорости. Результаты показали, что при скоростях электронов меньше некоторого критического значения удары упруги, а при критической скорости столкновения становятся неупругими, электроны теряют энергию, а атомы газа переходят в возбуждённое состояние. При дальнейшем увеличении скорости удары снова становились упругими, пока не достигалась новая критическая скорость. Наблюдаемое явление позволило сделать вывод о том, что атом может или вообще не поглощать энергию, или же поглощать в количествах равных разности энергий стационарных состояний^{[источник не указан 1010 дней]}.

Примечания[править | править код]

↑ Планетарная модель атома. Постулаты Бора Архивная копия от 21 февраля 2009 на Wayback Machine на Портале Естественных Наук Архивная копия от 26 ноября 2009 на Wayback Machine
↑ Боровский радиус Архивная копия от 11 сентября 2015 на Wayback Machine согласно CODATA

Литература[править | править код]

Борн М. Атомная физика, 2-е изд. — М.: Мир, 1967, 493 с.
Джеммер, Макс. Эволюция понятий квантовой механики / Пер. с англ. / Под ред. Л. И. Пономарёва. — М.: Наука, 1985. — С. 11. — 384 с.
Милантьев В. П. История возникновения квантовой механики и развитие представлений об атоме. — М.: Книжный дом «ЛИБРОКОМ», 2017, 246 с. ISBN 978-5-397-05872-8.

Источник

После
нескольких месяцев работы
Бор в 1913 г. опубликовал свою квантовую
теорию атома. Основу
этой теории составляют три постулата.

Первый
постулат Бора:

Атом
может находиться не во всех состояниях,
допускаемых
классической физикой, а только в особых,
квантовых (или
стационарных) состояниях, каждому из
которых соответствует своя определенная
энергия Е_n.
В стационарном
состоянии атом не излучает и не поглощает
энергию.

Второй
постулат Бора:

При
переходе атома из одного стационарного
состояния в
другое излучается или поглощается квант
света с энергией ћω,
равной
разности энергий стационарных состояний
(рис.25.5):

ћω
= |Е_n₂-Е_n₁|
(25.1)

Е_n₁–
энергия в начальном состоянии, Е_n₂–
энергия в конечном состоянии.

Третий
постулат Бора:

В стационарном
состоянии электрон может двигаться
только по такой («разрешенной») орбите,
радиус которой удовлетворяет условию:

m·υ·r=n·ћ
(25.2)

–
условие
стационарности электронных орбит, где
m·υ·r
— момент импульса электрона, n
— номер квантового состояния (n
=1, 2, 3, …).

Целое число n,
определяющее номер квантового состояния
и энергию атома в этом состоянии,
называется главным
квантовым числом.

Применив свою
теорию к простейшему из атомов — атому
водорода, Бор получил результаты,
полностью согласующиеся с экспериментальными
данными.

Рассмотрим
простейший атом — атом водорода. Он
состоит из ядра, в состав которого входит
один протон, и одного электрона,
вращающегося вокруг ядра по круговой
орбите. На электрон со стороны ядра
действует кулоновская сила притяжения,
сообщая ему центростремительное
ускорение, поэтому

(25.3)

[е — заряд электрона
и протона, ε_о
— электрическая постоянная].

Поскольку должен
выполняться первый постулат Бора,
воспользуемся условием стационарности
электронных орбит. Определим из него
скорость υ

(25.4)

возведем в квадрат
и подставим в (25.4). Из полученного
выражения найдем

отсюда радиус
орбит электрона в атоме водорода равен

(25.5)

Подставляя в (25.5)
значения констант и считая n
= 1, получаем значение первого боровского
радиуса, который является единицей
длины в атомной физике:

r_Б
= 0,528-10^-10
м.

§ 25.3 Энергия атома водорода

По боровской модели
ядро атома считается неподвижным,
поэтому полная энергия Е атома является
суммой кинетической энергии Е_к
вращения электрона и потенциальной
энергии Е_п
взаимодействия электрона с ядром:

(25.6)

Полученное значение
Е отрицательно, так как потенциальная
энергия двух зарядов, находящихся
на бесконечно большом расстоянии,
предполагается равной нулю. При сближении
зарядов потенциальная энергия уменьшается.

Каждое значение
энергии, которой обладает атом в том
или ином стационарном состоянии, называют
энергетическим
уровнем.
Чем больше n,
тем дальше от ядра находится электрон
и тем выше его энергетический уровень.

Энергетические
уровни атома принято изображать
горизонтальными линиями, а переходы
атома из одного стационарного состояния
в другое – стрелками (рис.25.6).

Когда атом переходит
с более высокого на более низкий
уровень (чему соответствует «перескок»
электрона на более близкую к ядру
орбиту), то происходит излучение кванта
света. При поглощении, наоборот, падающий
на атом квант (фотон) переводит атом
из состояния с меньшей в состояние с
большей энергией; сам фотон при этом
исчезает, а поглотивший его электрон
оказывается на более далекой от ядра
орбите.

Состояние
атома сn
=1 называют основным
или нормальным состоянием.
В этом состоянии энергия атома минимальна,
и он может находиться в нем (при
отсутствии внешних воздействий) сколь
угодно долго.

Все остальные
состояния с n>1
называют возбужденными.
В возбужденном состоянии атом может
находиться в течение очень малого
промежутка времени (порядка 10^-8
с), после чего самопроизвольно
переходит в основное состояние (сразу
или поэтапно, уровень за уровнем),
излучая при этом соответствующие кванты.

В основном
состоянии атом водорода обладает
энергией Е_і
= -13,6 эВ. При переходе в возбужденные
состояния его энергия возрастает.

Минимальную
энергию, которую нужно затратить для
удаления электрона с первой боровской
орбиты на «бесконечность», называют
энергией
ионизации W_і
или энергией связи атома водорода.

Таким образом, для
ионизации атома водорода, находящегося
в основном состоянии, ему необходимо
сообщить энергию ΔЕ
=W_і
= 13,6 эВ. Если же ему будет передаваться
энергия ΔЕ
<W_і,
то при ΔЕ=Е_n—Е_і
атом перейдет в состояние с энергией
Е_п,
а при ΔЕ ≠ Е_n—Е_іпоглощения
энергии не произойдет и атом останется
в прежнем состоянии.

Такой («скачкообразный»)
характер поглощения энергии должен
наблюдаться для атомов любого химического
элемента. Для атомов ртути он был
обнаружен уже в 1913 г. немецкими
физиками-экспериментаторами Д.
Франком и Г. Герцем. Их опыты подтвердили
существование в атомах дискретных
энергетических уровней, что сыграло
важнейшую роль в развитии квантовой
теории атома.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Квантовые постулаты Бора – это два основных допущения, введённые Н.Бором для объяснения устойчивости атома и спектральных закономерностей (в рамках модели атома Резерфорда).

Планетарная модель атома Резерфорда позволила объяснить результаты опытов по рассеянию α-частиц вещества, но она не способна объяснить факт существования атома и его устойчивость.

В соответствии с планетарной моделью электроны атома должны двигаться вокруг неподвижного ядра. Двигаясь вокруг ядра с центростремительным ускорением под действием силы притяжения к ядру, электрон должен, как и всякий ускоренно движущийся электрический заряд, излучать электромагнитные волны с частотой, равной частоте обращения электрона вокруг ядра.

Энергия электрона в атоме должна при этом непрерывно уменьшаться за счёт излучения. Сам электрон должен с каждым оборотом приближаться по спирали к ядру и упасть на него под действием электрической силы притяжения. При этом атом потеряет всю электронную оболочку, а также присущие ему физические и химические свойства. Кроме того, атом должен потерять спектр излучения частоты, то есть атом должен давать излучение с непрерывным (сплошным) спектром частот.

Эти результаты, полученные с помощью классической механики и электродинамики, находятся в резком противоречии с опытом, который показывает, что

Атомы являются весьма устойчивыми системами и в невозбуждённом состоянии могут существовать неограниченно долго, не излучая при этом электромагнитные волны
Спектр излучения атома является линейчатым (дискретным) – образованным из отдельных линий (от латинского discretus – прерывистый, состоящий из отдельных значений)

Всё это свидетельствует о том, что законы классический физики применить к электронам в атомах нельзя, поэтому необходимы новые представления о механизме излучения и поглощения атомами электромагнитных волн. В основе современной теории атома лежитквантовая механика – теория, устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов), а также связь величин, которые характеризуют частицы и системы, с физическими величинами, измеряемыми опытным путём.

В 1913 году датский физик Нильс Бор (1885 – 1962) ввёл идеи квантовой теории в ядерную модель атома Резерфорда и разработал теорию атома водорода, которая подтвердилась всеми известными тогда опытами. Бор сформулировал в виде постулатов основные положения новой теории, которые налагали лишь некоторые ограничения на допускаемые классической физикой движения. Однако последовательной теории атома Бор не дал. Впоследствии теория Бора была включена как частный случай в квантовую механику. В основе теории Бора лежат два постулата.

Первый постулат Бора: постулат стационарных состояний

Атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определённая энергия E_n. В стационарном состоянии атом не излучает.

Второй постулат Бора: правило частотe

Излучение света происходит при переходе атома из стационарного состояния с большей энергией E_k в стационарное состояние с меньшей энергией E_n. Энергия излученного фотона равна разности энергий стационарных состояний:

hv_kn = E_k — E_n

Частота излучения равна:

v_kn = (E_k — E_n) / h = (E_k / h) — (E_n / h)

Или, длина волны излучения λ равна:

1 / λ_kn = (1 / hc) (E_k — E_n)

Где h – постоянная Планка, с – скорость света в вакууме.

Если E_k > E_n, то происходит излучение фотона, если E_k < E_n, то происходит поглощение фотона, при котором атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией. Таким образом, для каждого атома имеется ряд строго определённых дискретных значений энергии, которыми он может обладать. Физические величины, например энергия и импульс, которые могут принимать лишь дискретные (квантовые) значения, носят название квантованные физические величины (квантование физических величин). При этом энергетические уровни атома – это возможные значения энергии атома.

Правило квантования орбит позволяет определить радиусы стационарных орбит:

mv_nr_n = nh’

где n = 1, 2, 3…, m – масса электрона, r_n – радиус n-ой орбиты, v_n – скорость электрона на этой орбите.

Число n – положительное число, которое называется главное квантовое число.

Величина (mv_n)r_n – момент импульса электрона.

h’ – это величина, которая равна:

h’ = h/2π = 1,05445887•10^-34 Дж•с

где h – постоянная Планка.

Главное квантовое число указывает номер орбиты, по которой может обращаться электрон.

Свои постулаты Н.Бор применил для построения теории простейшей атомной системы – атома водорода, состоящего из ядра – протона, и одного электрона. Эта теория также применима для водородоподобных ионов, то есть атомов с зарядом ядра Ze и потерявших все электроны, кроме одного (например, Li²⁺, Be³⁺ и т.п.). В предположении, что электрон движется по круговой орбите, постулаты Бора позволяют найти радиусы r_n стационарных, возможных орбит электрона. На электрон действует кулоновская сила:

F_k = (1 / 4πε₀) (ε² / r_n²)

Где е – модуль заряда электрона, равный заряду ядра, ε₀ = 8,85418782 * 10^-12 Ф/м – электрическая постоянная в единицах СИ.

Кулоновская сила сообщает электрону на орбите центростремительное ускорение:

a_цс = (v_n²) / r_n

Согласно второму закону Ньютона:

F_k = ma_цс

Поэтому

(mv_n²) / r_n = e² / (4πε₀r_n²)

Или

mv_n²r_n = e² / (4πε₀)

Используя правило квантования орбит mv_nr_n = nh’, можно получить выражения для возможных радиусов орбит. Исключая скорость v_n из предыдущего выражения, получим:

r_n = 4πε₀n²h’ / me² (так как h’ = h / 2π)

Таким образом, радиусы орбит электрона в атоме водорода прямо пропорциональны квадратам главного квантового числа n.

Наименьший радиус орбит при n = 1, то есть радиус первой орбиты в атоме водорода равен:

r₁ = 4πε₀h’ / me² = 0,528 * 10^-10 м = 0,528 Å

Радиус первой орбиты в атоме водорода носит название первый Боровский радиус и служит единицей длины в атомной физике.

Полная энергия Е электрона в атоме водорода, согласно механике Ньютона, равна сумме кинетической энергии Е_k и потенциальной энергии П взаимодействия электрона с ядром:

E = Е_k — П = (mv_n² / 2) — (e² / 4πε₀r_n)

Потенциальная энергия электрона в атоме отрицательна:

П = — (e² / 4πε₀r_n)

Так как нулевой уровень отсчёта берётся на бесконечности (рис. 1.3), а по мере приближения электрона к ядру его потенциальная энергия уменьшается. Взаимодействующие частицы – ядро и электрон – имеют заряды противоположных знаков.

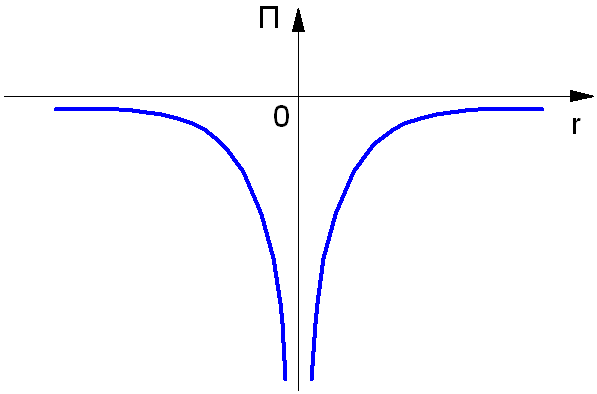
Рис. 1.3. Потенциальная энергия электрона в атоме.

Подставляя значение скорости

v_n² = — e² / 4πε₀mr_n

в выражение полной энергии, получим:

E = (m / 2) (e² / 4πε₀mr_n) — (e² / 4πε₀r_n)

Подставляя в эту формулу выражение для радиусов орбит, получим энергетические уровни электрона в атоме водорода (значения энергий стационарных состояний атома):

E_n = -(1 /(4πε₀)²) me⁴ / 2h’²n² = — (me⁴ / 8h²ε₀²) * (1 / n²), n = 1,2,3…

Энергия Е_n электрона в атоме водорода зависит от главного квантового числа n, которое определяет энергетические уровни электрона в атоме водорода.

Основное энергетическое состояние атома (нормальное состояние атома) – это энергетический уровень при n = 1.

Значение энергии, соответствующее первому (низшему) энергетическому уровню в атоме водорода равно:

E₁ = -(1 /(4πε₀)²) me⁴ / 2h’²λ = -2,485 * 10^-19 Дж = -13,53 эВ

В этом состоянии атом может находиться сколько угодно долго. Для того чтобы ионизировать атом водорода, ему нужно сообщить энергию 13,53 эВ, которая называется энергия ионизации.

Энергетические уровни при n > 1 – это возбуждённые энергетические состояния (возбуждённые состояния атома). Возбуждённое состояние атома является менее устойчивым, чем основное состояние. Время жизни атома в этом состоянии имеет порядок 10^-8 секунд. За это время электрон успевает совершить около ста миллионов оборотов вокруг ядра.

При переходе электрона с удалённой от ядра стационарной k-орбиты на ближайшую n-ую орбиту атом излучает фотон, энергия которогоhv_nk согласно второму постулату Бора определяется:

hv_kn = E_k — E_n = -(1 / (4πε₀)²) * (me⁴ / 2h’²) * [(1 / n²) — (1 / k²)] = (me⁴ / 8h²ε₀²) * [(1 / n²) — (1 / k²)]

Частота излучения атома водорода:

v_kn = (1 / (4πε₀)²) * (me⁴ / h’³) * [(1 / n²) — (1 / k²)] = R[(1 / n²) — (1 / k²)]

Где

R = (me⁴ / (4πε₀)²) * 4πh’³) = (me⁴ / 8h³ε₀²) = 3,288 * 10¹⁵ c^-1— постоянная Ридберга

Постоянная Ридберга определяется через постоянную Планка, массу и заряд электрона.

Длина волны излучения определяется соотношением:

1 / λ_nk = v_nk / c = (me⁴ / 8ε₀²h³c) * [(1 / n²) — (1 / k²)] = R_c[(1 / n²) — (1 / k²)]

Где

R_c = R / c = 1,0974 * 10⁷ м^-1 — также постоянная Ридберга

с = 3*10⁸ м/с – скорость света в вакууме.

Теоретическое значение R совпадает с экспериментальным значением, полученным из спектроскопических измерений.

Энергия обычно измеряется в электронвольтах (эВ). Электронвольт– это значение энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов в 1 В:

1 эВ = 1,6 * 10^-19 Кл * 1В = 1,6 * 10^-19 Дж

Источник

На прошлом уроке мы с вами рассматривали опыты Эрнеста
Резерфорда по рассеянию альфа-частиц, которые позволили учёному создать ядерную
(или планетарную) модель атома.

Однако при всей своей убедительности планетарная модель атома
оказалась внутренне противоречивой. По законам электродинамики движущийся
ускоренно заряд излучает электромагнитные волны. Следовательно, атом должен
непрерывно излучать электромагнитные волны. Излучение же связано с уменьшением
энергии электрона в поле ядра. Следствием этого должно явиться уменьшение
скорости движения и частоты вращения электронов вокруг ядра. Если частота
непрерывно изменяется, то спектр излучения атома должен быть сплошным.
Уменьшение скорости электрона должно привести к тому, что электрон будет
двигаться по спирали к ядру и в течение короткого времени упадёт на него, то
есть в этой модели атом должен быть неустойчивым.

Это находится в полном противоречии с экспериментальными
фактами, которые свидетельствуют о том, что:

·
атом является достаточно устойчивой системой;

·
атом излучает электромагнитные волны лишь при определенных
условиях, а не непрерывно;

·
а спектры излучения атомов являются линейчатыми.

Эти противоречия возникли потому, что к электронам в атомах
применяли законы классической физики, а, как мы уже с вами знаем, в микромире
действуют свои законы, отличные от законов макромира. Первым признал
невозможность применения законов классической физики к атомам датский учёный
Нильс Бор. Он ввёл элементы квантовой теории в модель атома Резерфорда и в 1913
году создал неклассическую теорию атома. В её основе лежала идея связать в
единое целое три результата, полученные в физике к тому времени.

Для решения этой задачи Бор, сохраняя классический подход к
описанию поведения электрона в атоме, выдвинул два предположения, которые мы
называем постулатами Бора. Сразу же отметим, что физический смысл этих
постулатов не только не мог быть объяснён в классической физике, но, более
того, находился в глубоком противоречии с классическим описанием движения
электрона в атоме.

В современном виде постулаты Бора формулируются следующим
образом.

Первый постулат Бора (постулат стационарных состояний):

атом может находиться в особых стационарных (квантовых)
состояниях, каждому из которых соответствует определенная энергия. Находясь в
стационарном состоянии, атом не излучает и не поглощает энергию.

Стационарные состояния можно пронумеровать, присвоив им
порядковые номера, причём каждому состоянию соответствует определенное
дискретное значение энергии. Согласно модели Бора стационарным состояниям атома
соответствуют определенные (разрешённые) орбиты, по которым электроны движутся
вокруг ядра. При движении по этим орбитам электроны не излучают
электромагнитные волны.

Первый постулат противоречит нашим представлениям о движении
в классической механике, так как мы знаем, что скорость тел изменяется
постепенно и может принимать любые значения. Бор вводит понятие квантования
скоростей и орбит электрона: скорости и радиусы орбит могут изменяться не
непрерывно, а имеют только определённый дискретный набор значений.

Второй постулат Бора ещё называют правилом частот:

атом может переходить из одного стационарного состояния в
другое. При этом переходе может испускаться или поглощаться квант
электромагнитного излучения, частота которого определяется разностью энергий
атома в данных состояниях:

Из формулы следует, что если электрон переходит с более
низкой орбиты на более высокую, то он поглощает квант энергии. Если же
наоборот, переход осуществляется с более высокой на более низкую орбиту, то
электрон излучает квант энергии.

Состояние атома, которому соответствует наименьшая энергия,
называется основным. А состояния, которым соответствуют большие значения
энергии, — возбуждёнными. В основном энергетическом состоянии атом может
находиться неограниченно долго, а в остальных стационарных состояниях порядка 10^–6
с. Это так называемое время жизни атома в возбуждённом состоянии.

Как следует из второго постулата Бора, частота излучения
атома не связана с частотой вращения электрона по орбите, она определяется
разностью значений энергии атома в начальном и конечном состояниях. Переход
атома из одного стационарного состояния в другое сопровождается
электромагнитным излучением определённой длины волны:

Для объяснения же эмпирических закономерностей в спектре
атома водорода эти два постулата были дополнены правилом квантования орбит,
которое иногда называют третьим постулатом Бора:

в стационарном состоянии атома электрон, движущийся по
круговой орбите, должен иметь квантованные (дискретные) значения момента
импульса, которые удовлетворяют условию:

В записанной формуле m — это масса электрона, υ — его скорость на n-й орбите, r_n — радиус стационарной орбиты, а n
= 1, 2, 3, … — это номер орбиты электрона.

Таким образом, постулаты Бора основывались на трёх
экспериментальных предпосылках — результатах исследования атомных спектров,
квантовой теории излучения, развитой Планком и Эйнштейном, и ядерной
(планетарной) модели атома Резерфорда.

Исходя из этих постулатов и используя планетарную модель
строения атома, Нильс Бор разработал количественную теорию атома водорода. Он
рассчитал радиусы стационарных орбит электрона в атоме водорода и вычислил
соответствующие им значения энергии.

Проделаем это и мы. Итак, согласно классическим
представлениям, электрон движется вокруг ядра под действием кулоновской силы,
которая сообщает ему центростремительное ускорение:

Согласно второму закону Ньютона, сила притяжения со стороны
ядра должна определяться произведением массы электрона и его
центростремительного ускорения:

С другой стороны, как упоминалось выше, сила притяжения к
ядру есть не что иное, как сила Кулона, определяемая, в данном случае,
отношением квадрата заряда электрона к квадрату радиуса орбиты:

Перепишем второй закон Ньютона с учётом наших рассуждений и
представим полученное выражение так, как это показано на экране:

Теперь запишем условие квантования орбит и выразим из него
скорость электрона:

Далее найдём выражение, для определения радиусов разрешённых стационарных
орбит электрона в атоме водорода:

Как видно из формулы, радиусы стационарных устойчивых
орбит возрастают пропорционально квадратам номеров орбит:

Для примера давайте с вами определим радиус первой боровской
орбиты электрона.

Этот радиус, ближайший к атомному ядру, определяет размер
атома водорода в основном состоянии.

Так как радиус орбиты может принимать только дискретные
(квантованные) значения, то и энергия атома в различных стационарных состояниях
может также принимать только дискретные значения.

Итак, очевидно, что энергия электрона в атоме водорода равна
сумме его кинетической энергии при движении по круговой орбите и потенциальной
энергии в электростатическом поле ядра:

(поскольку взаимодействуют частицы, имеющие заряды
противоположных знаков, то между ними действует сила кулоновского притяжения и
потенциальная энергия их взаимодействия отрицательна).

Подставим в эту формулу значения скорости электрона и радиуса
орбиты:

Проведя все необходимые математические вычисления и
преобразования, получим формулу для определения энергии электрона, находящегося
на n-й орбите:

Из этой формулы видно, что энергия атома водорода квантована
и определяется только номером орбиты.

Давайте рассчитаем значение энергии электрона в атоме
водорода на первой боровской орбите.

Для наглядного представления возможных энергетических
состояний атомов используются энергетические диаграммы, на которых каждое
стационарное состояние атома отмечается горизонтальной линией, называемой
энергетическим уровнем.

Ниже всех на диаграмме располагается энергетический уровень,
соответствующий основному состоянию (состояния с минимальной энергией).
Энергетические уровни возбуждённых состояний располагаются над основным уровнем
на расстояниях, пропорциональных разности энергий возбуждённого и основного
состояний. Переходы атома из одного состояния в другое изображаются
вертикальными линиями между соответствующими уровнями на диаграмме. Направление
перехода обозначается стрелкой.

Из диаграммы видно, что чем электрон дальше от ядра, тем на
меньшую величину отличаются соседние уровни энергии, то есть густота
энергетических уровней растёт. Квантовые скачки при этом уменьшаются,
вследствие чего переходы между стационарными состояниями атома всё больше и
больше становятся «похожими» на непрерывное изменение энергии, то есть энергия
становится почти непрерывной величиной, как и в классической теории.

Если попытаться выразить частоту излучения атома водорода при
его переходе с одного энергетического уровня на другой, то окажется, что полученное
выражение полностью совпадает с эмпирической формулой Бальмера — Ридберга:

А вычисленная постоянная Ридберга по этой формуле показывает
хорошее совпадение с найденной из эксперимента.

В 1922 году Нильсу Бору была присуждена Нобелевская премия
«за заслуги в исследовании строения атомов и излучения», так как его исследования
фактически положили начало новому этапу развития спектроскопии, которая из
эмпирической науки превратилась в эффективный метод изучения атомной структуры.
Спустя пол века по этому поводу Бор скажет: «Я увидел путь рождения спектров!»

Итак, что же дала нам модель атома водорода по Бору. Во-первых,
она позволила вычислить энергию ионизации атома водорода, хорошо согласующуюся
с экспериментом. А во-вторых, дала мощный толчок к объяснению закономерностей
периодической системы химических элементов Менделеева. Согласно модели атома
Бора электроны движутся по определенным орбитам, образующим различные группы —
электронные оболочки. Структура электронных оболочек определяет химические
свойства элементов, которые периодически повторяются по мере заполнения
оболочек электронами. Это позволило «предсказывать» свойства ранее неизвестных
элементов. Так, например, был открыт элемент га́фний, по своим свойствам
аналогичный цирконию. Модель атома Бора также объяснила основные закономерности
спектра атома водорода, хотя частично сохранила классический характер,
поскольку в ней предполагалось, что электроны движутся по орбитам вокруг ядра.

Оставалось, однако, неясным, от чего зависит интенсивность
излучения тех или иных частот. Без ответа остался вопрос, почему совершаются те
или иные переходы. Но самым серьёзным недостатком модели атома Бора была
невозможность построить теорию более сложных атомов (даже атома гелия — одного
из простейших атомов, непосредственно следующего за атомом водорода). Но модель
атома Бора явилась переходным этапом на пути к созданию современной теории
атомных и ядерных явлений — квантовой механики.

Источник

Полуклассическая теория Бора[править | править код]

Формула Зоммерфельда — Дирака[править | править код]

Достоинства теории Бора[править | править код]

Недостатки теории Бора[править | править код]

Экспериментальное подтверждение теории Бора[править | править код]

Примечания[править | править код]

Литература[править | править код]

§ 25.3 Энергия атома водорода

Первый постулат Бора: постулат стационарных состояний

Второй постулат Бора: правило частотe

Вам также может понравиться

Как найти все острова в сабнатика

Как найти свой логин на майле

Как найти плотность энергии формула

Добавить комментарий Отменить ответ