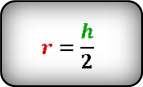Как найти радиус пески

Как найти радиус пески

Нужный объем песка постоянно рассчитывают строители при выполнении широкого спектра работ:

  • засыпки и поднятия участков;
  • строительстве фундаментов и заборов;
  • формировании стяжки;
  • заливке отмостки;
  • приготовлении бетона;
  • благоустройстве территорий.
Точный расчет необходимого объема песка экономит время и деньги
Точный расчет необходимого объема песка экономит время и деньги

В большинстве случаев для строительных целей используют карьерный или речной песок. Удельный вес 1 м³ карьерного песка – 1 500 кг, речного – 1 630 кг.

Речной песок более тяжелый, что объясняется меньшим размером зерен и большей плотностью материала. Приобретать песок рекомендуется в сухую погоду, когда в нем содержится минимум избыточной влаги.

РАСЧЕТ ОБЪЕМА ПЕСКА ДЛЯ ЗАСЫПКИ

Предположим, нам нужно засыпать участок площадью 6 соток (600 м²), подняв его на уровень 0,5 м.

Для определения объема песка следует умножить площадь участка на высоту засыпки. В нашем расчете – 600 х 0,5 = 300 м³.

После засыпки песок уляжется, на это нужно сделать поправку. Коэффициент уплотнения колеблется в пределах 1,05–1,3, в зависимости от вида песка. Для нашего примера возьмем среднюю величину 1,1, то есть добавим к рассчитанному объему еще 10 %. В результате получим 300 х 1,1 = 330 м³ песка.

Песок доставляют на самосвалах с разным объемом кузова
Песок доставляют на самосвалах с разным объемом кузова

Заказывая материал, нужно обязательно уточнить, каким транспортом его доставят. В кузов КамАза, к примеру, помещается 12 м³ песка, МАЗа – 6 м³, ЗИЛа – 3 м³. При загрузке с горкой объем может увеличиться до 1,5 раза.

РАСЧЕТ ОБЪЕМА ПЕСКА ДЛЯ БЕТОННОЙ СМЕСИ

При расчете количества песка для строительной смеси при создании фундаментов или стяжки нужно учитывать марку цемента.

Из-за неправильного объема песка снизится качество бетона
Из-за неправильного объема песка снизится качество бетона

Сначала вычисляют необходимый объем бетона по формуле, приведенной выше. Исходя из класса бетона определяют требуемое количество песка.

Рассчитать его можно двумя способами:

  • По долевому соотношению песка и цемента

Для разных марок цемента используют разные пропорции. Показатель включения песка варьируется от 2–4,5 : 1.

Предположим, мы используем цемент марки М-200, для которого принято соотношение 2,8 : 1. Значит, на 100 кг цемента нужно взять 280 кг песка.

  • По процентному содержанию в бетоне

Зная необходимый объем бетона, просчитываем объем песка, исходя из его процентного содержания в смеси. В зависимости от класса бетона доля песка колеблется в пределах 29–36 %. Значит, нам потребуется минимум 29 м³ песка.

Расчет объема песка в конусной насыпи

Представим ситуацию, когда песок уже выгружен из самосвала и точно неизвестно, сколько его было в каждой машине. Просчитать объем конусной насыпи простым сложением не получится.

Для расчета объема песка в конусной насыпи нужно замерить ее радиус и высоту
Для расчета объема песка в конусной насыпи нужно замерить ее радиус и высоту

Узнать точный объем песка в конусной насыпи можно по формуле: V = ⅓π х R² х H, где R – радиус конуса, H – его высота, π = 3,14.

КАК ПОСЧИТАТЬ НУЖНЫЙ ОБЪЕМ ПЕСКА

Предположим, высота насыпи 1 метр, а радиус – 1,5 м. Рассчитываем:

КАК ПОСЧИТАТЬ НУЖНЫЙ ОБЪЕМ ПЕСКА

Конечно, песок не дает идеального конуса, но примерно оценить объем таким образом возможно. А зная точный объем необходимого и имеющегося в наличии песка, проще планировать расход и поставки. Не будет простоев в работе, жесткой экономии, вынужденного снижения качества бетона и, соответственно, прочности готовых конструкций.

Источник

Как найти радиус окружности

Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.

Выбирайте формулу в зависимости от известных величин.

Через площадь круга

  1. Разделите площадь круга на число пи.
  2. Найдите корень из результата.
Иллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
  • π (пи) — константа, равная 3,14.

Через длину окружности

  1. Умножьте число пи на два.
  2. Разделите длину окружности на результат.
Иллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • P — длина окружности (периметр круга).
  • π (пи) — константа, равная 3,14.

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Иллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • D — диаметр.

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

Иллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
  • a, b — стороны вписанного прямоугольника.

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

Иллюстрация: Лайфхакер
  • r — искомый радиус окружности.
  • a — сторона описанного квадрата.

Через стороны и площадь вписанного треугольника

  1. Перемножьте три стороны треугольника.
  2. Разделите результат на четыре площади треугольника.
Иллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • a, b, с — стороны вписанного треугольника.
  • S — площадь треугольника.

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

Иллюстрация: Лайфхакер
  • r — искомый радиус окружности.
  • S — площадь треугольника.
  • p — полупериметр треугольника (равен половине от суммы всех сторон).

Через площадь сектора и его центральный угол

  1. Умножьте площадь сектора на 360 градусов.
  2. Разделите результат на произведение пи и центрального угла.
  3. Найдите корень из полученного числа.
Иллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • S — площадь сектора круга.
  • α — центральный угол.
  • π (пи) — константа, равная 3,14.

Через сторону вписанного правильного многоугольника

  1. Разделите 180 градусов на количество сторон многоугольника.
  2. Найдите синус полученного числа.
  3. Умножьте результат на два.
  4. Разделите сторону многоугольника на результат всех предыдущих действий.
Иллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
  • N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✂️📌

  • Как найти периметр прямоугольника
  • Как научить ребёнка считать играючи
  • Как перевести обычную дробь в десятичную
  • 6 способов посчитать проценты от суммы с калькулятором и без
  • 9 логических задач, которые по зубам только настоящим интеллектуалам

Источник

Определите
коэффициент фильтрации водоносных
песков по результатам откачки воды из
одиночной скважины совершенного типа.
По величине коэффициента фильтрации
определите водопроницаемость и
водопроводимость водоносного песка.
Сделайте
схематический рисунок. Данные для
расчётов приведены в таблице 7.

Таблица
7 – Исходные
данные к заданию 6

№
варианта

Мощность

водоносного

горизонта,

Н,
м

Дебит

скважины,

Q,
м3/сут

Понижение

уровня
воды

в
скважине,

S,
м

Радиус
депрессионной воронки,

R,
м

Радиус

скважины,

r,
м

0

12

508

4

98

0,1

1

10

350

5

58

0,2

2

24

2478

12

285

0,3

3

9

490

3

74

0,1

4

12

500

7

80

0,2

5

35

6770

20

520

0,3

6

18

809

10

115

0,2

7

26

3003

20

350

0,3

8

7

150

3

35

0,1

9

28

2475

16

325

0,2

10

8

170

2

25

0,1

11

15

450

11

62

0,3

12

17

550

8

77

0,1

13

27

2200

10

255

0,3

14

23

2100

15

220

0,3

15

25

2950

12

395

0,3

16

16

725

2

102

0,2

17

14

613

9

72

0,1

18

29

2902

11

389

0,3

19

37

6800

5

578

0,3

20

21

2350

7

401

0,3

Пример
решения задачи для варианта № 0

Рисунок
6 – Схема расчёта гидрогеологических
параметров для совершенной скважины:
а) стандартная; б) для конкретных условий

Дано:

Н
= 12 м;

Q
= 508 м3/сут;

S
= 4 м;

R
= 98 м;

r
= 0,1 м

Найти:Кф,
Кв

Решение:

Коэффициент
фильтрации можно определить двумя
способами, используя формулу Дюпюи:

а)
по величине слоя воды в скважине после
откачки h,
м;

б)
через последовательное понижение уровня
воды в скважине при откачке S,
м.

Подставив
в формулу Дюпюи числовое значение π
= 3,14 и заменив
натуральные логарифмы десятичными,
получим формулу, более удобную для
расчётов:

или

,

откуда

,где

Кф
– коэффициент
фильтрации, м/сут;

Q
– дебит скважины, м3/сут;

R–
радиус депрессионной воронки, м;

r
– радиус скважины, м;

H
– мощность водоносного горизонта, м;

h
– слой воды в скважине после откачки,
м.

По
условию задачи неизвестна величина h.
При решении задачи первым способом ее
находят вычитанием понижения уровня
воды в скважине после откачки из мощности
водоносного горизонта h
= Н – S (рисунок
6).

Подставив
числовые значения в любую из вышеприведенных
формул, определим коэффициент фильтрации
по слою воды в скважине после откачки:

При
решении задачи вторым способом в самом
начале нужно разложить разность квадратов
(Н2
– h2)
на произведение суммы и разности этих
чисел. Тогда формула примет следующий
вид:

Поскольку
h = H – S,
то S = H – h.
Подставим в первых скобках (Н
– S) вместо
h,
во вторых – только значение S,
получим для расчёта следующую формулу:

Судя
по величине коэффициента фильтрации
водоносного горизонта – 13,90
м/сут, это
средневодопроницаемые пески.

Водопроводимость водоносного горизонта
равна:

Вывод:
Кф
= 13,90 м/сут;
Кв
= 166,80 м2/сут;
средневодопроницаемые
пески.

Задание 7

Для
определения гидрогеологических
параметров грунтового водоносного
горизонта мощностью Н был заложен куст
совершенных скважин, состоящий из
центральной (Ц скв.) и двух наблюдательных
скважин (скв. 1) и (скв. 2). Они расположены
в плане на одной прямой на расстоянии
соответственно L1
 и L2
от центральной. Из центральной скважины
производилась откачка грунтовой воды
с определением дебита Q,
а в наблюдательных замерялись понижения
уровней S1
и S2
(рисунок
7).

Постройте
схему и определите коэффициент фильтрации
песков, коэффициент водопроводимости
водоносного слоя и радиус влияния.
Данные для
расчётов приведены в таблице 8.

Таблица
8 – Исходные
данные к заданию 7

№
варианта

Мощность
водоносного горизонта,

Н,
м

Дебит

центр.

скв.,

Q,
м3/сут

Расстояние
скв. 1 от центр.,

L2,
м

Расстояние
скв. 2 от центр.,

L2
,
м

Понижение
уровня воды в скв.1,

S1,

м

Понижение
уровня воды в скв.2,

S2,
м

0

6,5

65

18

38

3,0

2,1

1

12,7

200

16

35

3,1

1,5

2

12,9

300

26

40

4,9

2,9

3

15,1

320

20

80

5,5

2,5

4

18,3

400

27

150

4,8

2,8

5

7,3

90

17

90

4,9

1,9

6

10,8

420

11

50

2,8

2,0

7

16,0

390

37

75

2,7

2,0

8

17,0

290

24

85

4,8

1,8

9

14,0

180

15

90

3,0

2,1

10

15,7

220

40

120

4,0

2,2

11

14,2

190

45

130

3,0

1,2

12

13,3

170

35

95

2,6

0,9

13

12,4

75

10

60

2,2

0,6

14

11,7

90

22

82

3,2

1,5

15

14,4

102

32

92

2,4

1,2

16

12,6

122

34

99

2,3

0,8

17

13,7

150

36

109

2,1

1,2

18

13,0

140

42

102

1,9

0,5

19

15,3

350

50

150

2,7

1,7

20

15,0

295

70

220

2,5

1,1

Пример
решения задачи для варианта №0

Рисунок
7 – Схема расчёта гидрогеологических
параметров для куста совершенных
скважин: а) стандартная; б) для конкретных
условий

Дано:

Н
= 6,5 м;

Q
= 65 м3/сут;

L1
= 18 м;

L2
= 38 м;

S1
= 3,0 м;

S2=
2,1 м

Найти:
Кф;
Кв;
R

Решение:

Коэффициент
фильтрации можно вычислить по
преобразованной формуле Дюпюи:

Коэффициент
водопроводимости слоя равен произведению
коэффициента фильтрации на мощность
слоя:

Радиус
влияния можем вычислить из уравнения:

откуда
R
=
102,34
= 218,78 м.

Вывод:
Кф
= 2,21 м/сут; Кв
= 143,65 м2/сут;
R
= 218,78
м.

Задача 8

По
данным, приведенным в таблице 9, постройте
схему и определите приток воды к
совершенной скважине с круговым контуром
питания при горизонтальном водоупоре
(рисунок 8),
пропущенные
значения необходимо вычислить.

Таблица
9 – Исходные
данные к заданию 8

№

варианта

Абсолютные

отметки,

м

глубинаУГВ

м

Столб

воды
в

скваж.

h
, м

Коэф.

фильтрации

Кф,
м/сут

Понижение

уровня
воды

в
скважине,

S,
м

Расстояние

от
скваж.

до
водоёма,

L,
м

Диаметр

скважины,

d,
мм

0

–
устья скваж.

66,0;

–
статич.

уровня

59,2;

–
динамич.

уровня
?;

–
кровли

водоупора

45,5

?

?

12,4

5,5

77

152

1

?

?

11,4

6,5

56

305

2

?

?

6,8

3,2

73

208

3

?

?

12,0

4,2

42

114

4

?

?

4,9

3,7

69

208

5

?

?

0,7

6,0

80

152

6

?

?

0,2

4,3

54

152

7

?

?

3,8

8,9

37

305

8

?

?

11,6

6,2

99

208

9

?

?

14

5,9

74

208

10

?

?

6,5

4,6

62

114

11

–
устья скваж

95,6;

–
статич.

уровня
?;

–
динамич.

уровня
?;

–
кровли

водоупора

75,5

?

12,4

4,5

3,2

50

208

12

?

10,8

16,5

11,2

62

114

13

?

11,1

7,4

7,8

121

208

14

?

13,8

4,6

5,8

68

152

15

?

3,9

7,1

4,7

65

114

16

?

6,8

5,5

5,0

84

208

17

?

7,9

10,4

3,7

91

305

18

?

6,5

1,4

0,9

82

114

19

?

8,5

0,8

7,4

49

208

20

?

2,9

3,2

5,8

50

152

Пример
решения задачи для варианта № 0

Рисунок
8 – Схема расчёта гидрогеологических
параметров для совершенной скважины с
круговым контуром питания: а) стандартная;
б) для конкретных условий

R
– радиус депрессионной воронки (радиус
влияния), м;

L
– расстояние от скважины до водоёма,
м;

r
– радиусскважины, мм;

S
– понижение уровня подземных вод, м;

H
– мощность водоносного горизонта, м;

h
– мощность слоя воды в скважине после
откачки, м;

а.о.у.
– абсолютная отметка устья скважины,
м;

а.о.с.у.
– абсолютная отметка статического
уровня грунтовых вод, м;

а.о.д.у.
– абсолютная отметка динамического
уровня грунтовых вод, м;

а.о.к.в.
– абсолютная отметка кровли водоупора
(или подошвы водоносного горизонта), м.

Дано:

Абс.
отм. устья 66,0 м;

Абс.
отм. статич. уровня 59,2 м;

Абс
отм. кровли водоупора 45,5 м;

S
= 5,5 м;

Кф
= 12,4 м/сут;

L
= 77 м;

d
= 152 мм

Найти:h;
абс. отм. динам. уровня; глубину залегания
УГВ; q

Решение:

Находим
пропущенные в варианте значения.

Определяем
динамический уровень в скважине, для
этого из статического уровня вычитаем
понижение S,
то есть: 59,2
– 5,5 = 53,7, м;

Определяем
глубину залегания статического уровня,
для этого из абсолютной отметки устья
вычитаем абсолютную отметку УГВ,
то есть: 66,0 –
59,2 = 6,8
м;

Определяем
столб воды в скважине после откачки
h,
для этого из абсолютной отметки
динамического уровня вычитаем абсолютную
отметку кровли водоупора: h
= 53,7 – 45,5 =
8,2 м.

Определяем
мощность водоносного горизонта:

–
через понижение S
и оставшийся после откачки столб воды
h:

H=
S+ h
= 5,5 + 8,2 = 13,7
м;

–
через разность абсолютных отметок
статического уровня УГВ и кровли
водоупора:

H=
а.о.с.у. – а.о.к.в. = 59,2
– 45,5 = 13,7 м.

Составим
расчётную схему (рисунок 7).

Определим
радиус влияния R
по формуле:

отсюда
0,5R = 71,68
м.

Так
как L
больше 0,5R,
то для расчёта единичного притока к
совершенной скважине, используем
следующую формулу:

В
случае если L
(расстояние от центра скважины до
водоёма) будет меньше или равно 0,5R,
то используется формула:

Диаметры
скважин даны в миллиметрах, поэтому
находим радиус скважины r
(мм) и переводим
это значение в метры.

Вывод:
h
= 8,2м; абс.
отм. динам. уровня
53,7м;
глубина УГВ
6,8м; q=624м3/сут

Задача 9

По
данным, приведенным в таблице 10,
постройте
схему (рисунок 9) и определите приток
воды в совершенную скважину, вскрывшую
напорные воды,
пропущенные
значения необходимо вычислить.

Таблица
10 – Исходные
данные к заданию 9

№

варианта

Абсолютные

отметки,

м

Мощность
водоносного слоя, м

Напор
над подошвой верхнего водоупора, м

Напор
над кровлей нижнего водоупора, м

Понижение

уровня
воды в скважине,

S,
м

Коэфф.
фильтрации

Кф,
м/сут

Диаметр

скважины

d,
мм

0

–
устья скв. 42,5;

–
подошва верхнего водоупора ?;

–
кровля нижнего водоупора 13,4;

–
пьезометр. уровень 39,6;

–
динамич. уровень водоупора 36,1

?

15,2

?

?

9,6

305

1

?

14,2

?

?

11,4

305

2

?

20,1

?

?

6,8

208

3

?

16,4

?

?

12,0

114

4

?

12,2

?

?

4,9

208

5

?

13,5

?

?

0,7

152

6

?

18,8

?

?

0,2

152

7

?

14,8

?

?

3,8

305

8

?

15,6

?

?

11,6

208

9

?

16,2

?

?

14

208

10

?

13,7

?

?

6,5

114

11

–
устья
скв. 73,4;

–
подошва верхнего водоупора 46,3;

–
кровля нижнего водоупора ?;

-пьезометр.
уровень ?;

-динамич.
уровень водоупора 63,8

15,9

22,8

?

?

4,5

208

12

12,3

18,9

?

?

16,5

114

13

17,2

21,3

?

?

7,4

208

14

15,4

26,2

?

?

4,6

152

15

19,2

22,4

?

?

7,1

114

16

14,1

19,7

?

?

5,5

208

17

14,7

19,1

?

?

10,4

305

18

13,6

23,5

?

?

1,4

114

19

9,8

18,3

?

?

0,8

208

20

18,8

21,4

?

?

3,2

152

Пример
решения задачи для варианта № 0

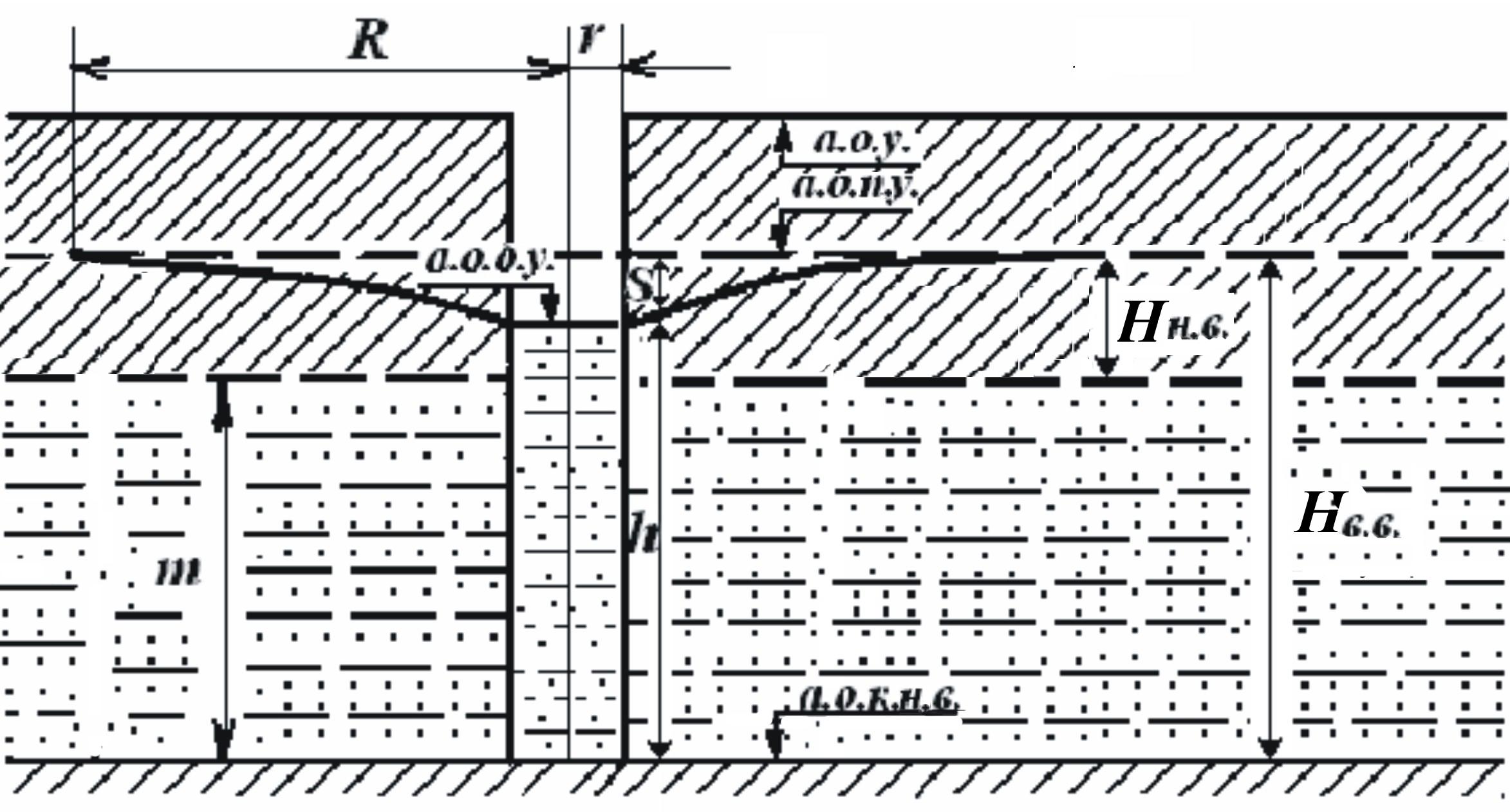
Рисунок
9 – Схема притока напорных вод к
артезианской скважине

R
– радиус депрессионной воронки (радиус
влияния), м;

r
– радиус скважины, мм;

S
– понижение уровня подземных вод, м;

m
– мощность
водоносного горизонта, м;

h
– мощность слоя воды в скважине после
откачки, м;

Нвв
– напор над подошвой верхнего водоупора,
м;

Ннв
– напор
над подошвой нижнего водоупора, м;

а.о.у.
– абсолютная отметка устья скважины,
м;

а.о.п.у.
– абсолютная отметка пьезометрического
уровня вод, м;

а.о.д.у.
– абсолютная отметка динамического
уровня напорных вод, м;

а.о.к.н.в.
– абсолютная отметка кровли нижнего
водоупора, м.

Дано:

Абс.
отм. устья 42,5 м;

Абс.
отм. пьез. уровня 39,6 м;

Абс.
отм. динам. уровня 36,1 м;

Абс
отм. кровли нижнего водоупора 13,4 м;

Нвв
=15,2
м;

Кф
= 9,6 м/сут;

d
= 305 мм

Найти:S,
h;
глубину залегания УГВ; Ннв;
абс. отм. подошвы верхнего водоупора;
m;
R;
 q

Решение:

Находим
пропущенные в варианте значения.

Определяем
понижение уровня подземных вод, для
этого из статического уровня вычитаем
динамический уровень, то есть: S
= 39,2 – 36,1 =
3,5 м.

Определяем
столб воды в скважине после откачки
h,
для этого из абсолютной отметки
динамического уровня вычитаем абсолютную
отметку кровли нижнего водоупора: h
= 36,1 – 13,4 =
22,7 м.

Определяем
глубину залегания УГВ,
для этого из абсолютной отметки устья
вычитаем абсолютную отметку
пьезометрического уровня, то есть: 42,5
– 39,6 = 2,9 м.

Определяем
напор над подошвой нижнего водоупора,
для этого абсолютной отметки статического
уровня вычитаем абсолютную отметку
кровли нижнего водоупора: 39,6 – 13,4 = 26,2
м.

Абсолютную
отметку подошвы верхнего водоупора
определяем как разность абсолютной
отметки пьезометрического уровня и
высоты напора над подошвой верхнего
водоупора: 39,6 – 14,2 = 25,4 м.

Мощность водоносного
пласта вычисляют как разность абсолютных
отметок подошвы верхнего и кровли
нижнего водоупоров:

m
= 25,4 – 13,4 =
12,0 м

Вычисляем радиус
депрессионной воронки:

R=10
·S
·√
Кф
= 10
·3,5
·√9,6
= 108,4
м

Определяем приток
воды в совершенную скважину, вскрывшую
напорные воды по формуле:

Вывод:
S
= 3,5
м; h
= 22,7 м;
глубина УГВ
2,9 м; Ннв=26,2
м; абс. отм.
подошвы верхнего водоупора
25,4 м;
m
= 12,0
м;
R=108,4
м;
q=624
м3/сут

Задача 10

Определить
приток грунтовой воды к совершенной
канаве (траншее, дрене) с 2-х сторон и с
одной стороны. Привести схематический
рисунок канавы с гидрогеологическими
параметрами (рисунок 10). После определения
притока рассчитайте величину
водопроводимости, удельный дебит,
охарактеризуйте грунт по водопроницаемости
(величине Кф).
Данные для расчётов приведены в таблице
11.

Таблица
11 – Исходные
данные к заданию 10

№
варианта

Длина
канавы

L,
м

Глубина
залег. УГВ,

м

Мощность

водоносн.

слоя,

Н,
м

Абс.
отметка,

Радиус
влияния канавы,

R,
м

Коэф.
фильтр.,

Кф,
м/сут

поверхн.

земли

динамич.
уровня

0

117

1,1

4,4

65,2

61,7

20

5,5

1

94

1,5

3,5

70,3

67,5

10

2,7

2

100

1,3

3,6

62,5

57,9

36

9,9

3

85

1,4

2,7

60,1

56,9

28

7,1

4

95

1,6

3,8

59,4

56,1

16

4,3

5

145

1,8

2,9

50,8

46,4

25

6,4

6

50

1,9

4,0

61,2

58,7

36

2,5

7

100

0,9

2,6

63,3

60,1

23

6,8

8

126

0,8

4,7

66,7

61,4

47

10

9

59

1,0

3,5

68,4

65,2

14

4,9

10

45

1,1

4,4

75,1

71,7

59

3,7

11

142

1,3

3,7

71,5

65,6

48

11

12

133

2,0

3,9

74,4

67,7

38

10,3

13

87

1,7

3,2

73,8

70,35

25

7,4

14

140

2,2

3,4

80,3

73,3

39

11,3

15

148

2,1

2,9

84,6

77,7

28

10,7

16

75

1,9

4,5

72,5

70,0

28

7,8

17

48

1,1

2,7

82,5

80,05

14

2,2

18

45

1,4

4,8

74,4

70,45

15

3,2

19

53

1,6

3,9

81,6

77,5

17

4,4

20

80

1,7

4,1

64,2

61,1

23

6,5

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Найти радиус окружности печи

Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.

Номер печи

Объём помещения (куб. м)

Масса (кг)

Стоимость (руб.)

дровяная

18 000

дровяная

19 500

электрическая

15 000

Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 5700 руб.

Масса (кг)

Номер печи

Отранжируем номера печей по их массе в соответствии с таблицей, получим:

15 кг – 3; 40 кг – 1; 48 кг – 2.

Задание 2. Найдите суммарную площадь стен парного отделения строящейся бани (без площади двери). Ответ дайте в квадратных метрах.

Имеем парное отделение с размерами 3,5 м x 2,2 м и высотой стен 2 м. Также в нем есть дверь шириной 0,6 м = 60 см и высотой 1,8 м.

Сначала найдем площадь стен с учетом площади двери, получим:

м2

И, затем, вычтем площадь двери:

м2

Задание 3. На сколько рублей покупка дровяной печи, подходящей по объёму парного отделения, обойдётся дешевле электрической с учётом установки?

Вычислим объем парного отделения как объем прямоугольного параллелепипеда со сторонами 3,5 x 2,2 x 2 м, получим:

м3

Подойдет или дровяная печь 2 или электрическая 3. С учетом установки электрическая печь стоит:

15 000 + 5700 = 20 700 руб,

а дровяная – 19 500 руб. Разность в стоимости, равна:

20700 – 19500 = 1200 руб.

Задание 4. В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 10 %, на печь номер 2 — 35 %, на печь номер 3 — 25%. Сколько рублей стоила печь номер 1 в прошлом году?

Стоимость 1-й печи со скидкой в 10%, равна 18 000 руб, следовательно, ее стоимость без скидки, равна:

руб.

Задание 5. Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.

Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.

Радиус закругления (гипотенузу) можно найти из прямоугольного треугольника с катетами 60 см и 25 см. По теореме Пифагора, имеем:

см

  • Вариант 1
  • Вариант 1. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
    • 1-5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 2
  • Вариант 2. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
    • 1-5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 3
  • Вариант 3. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
    • 1-5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 4
  • Вариант 4. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
    • 1-5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 5
  • Вариант 5. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
    • 1-5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 6
  • Вариант 6. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
    • 1-5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 7
  • Вариант 7. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
    • 1-5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 8
  • Вариант 8. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
    • 1-5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 9
  • Вариант 9. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
  • Задания 1-5 полностью совпадают с Вариант 1. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
  • Вариант 10
  • Вариант 10. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
  • Решения заданий по номерам
  • Задания 1-5 полностью совпадают с Вариант 2. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25

  • Внимание! Нумерация заданий в сборнике 2021 отличается от сборника 2020

  • Вариант 11
  • Задания совпадают с Вариант 1. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 25
  • Вариант 12
  • Задания совпадают с Вариант 2. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 25
  • Вариант 13
  • Задания 1-5 совпадают с Вариант 19. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 3. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 23
  • Вариант 14
  • Задания 1-5 совпадают с Вариант 20. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 4. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 23
  • Вариант 15
  • Задания 1-5 совпадают с Вариант 13. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 5. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 25
  • Вариант 16
  • Задания 1-5 совпадают с Вариант 14. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 6. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 25
  • Вариант 17
  • Задания 1-5 совпадают с Вариант 5. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 1. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 14
  • Вариант 18
  • Задания 1-5 совпадают с Вариант 6. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 2. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 14
  • Вариант 19
  • Задания совпадают с Вариант 3. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 8
    • 14
    • 24
  • Вариант 20
  • Задания совпадают с Вариант 4. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 8
    • 14
  • Вариант 21
  • Задания совпадают с Вариант 5. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 8
    • 14
    • 21
  • Вариант 22
  • Задания совпадают с Вариант 6. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 8
    • 14
    • 21
    • 22
    • 23
  • Вариант 23
  • Задания совпадают с Вариант 7. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1
    • 8
    • 14
    • 25
  • Вариант 24
  • Задания совпадают с Вариант 8. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1
    • 8
    • 14
    • 25
  • Вариант 25
  • Задания совпадают с Вариант 9. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1
    • 14
  • Вариант 26
  • Задания совпадают с Вариант 10. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1
    • 14
  • Вариант 27
  • Задания 1-5 совпадают с Вариант 17. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 11. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 14
    • 25
  • Вариант 28
  • Задания 1-5 совпадают с Вариант 18. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 12. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 14
    • 24
    • 25
  • Вариант 29
  • Задания совпадают с Вариант 13. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 8
    • 14
    • 25
  • Вариант 30
  • Задания совпадают с Вариант 14. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1
    • 8
    • 25
  • Вариант 31
  • Задания 1-5 совпадают с Вариант 29. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 15. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 8
    • 14
  • Вариант 32
  • Задания 1-5 совпадают с Вариант 30. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 16. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 8
    • 14
  • Вариант 33
  • Задания совпадают с Вариант 17. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 14
  • Вариант 34
  • Задания совпадают с Вариант 18. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 1-5
    • 14
  • Вариант 35
  • Задания 1-5 совпадают с Вариант 15. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 19. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 14
  • Вариант 36
  • Задания 1-5 совпадают с Вариант 16. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 20. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 14

Найти радиус окружности печи

Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.

Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (см. рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.

Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.

Номер печи Тип Объем помещения Масса Стоимость
1 Дровяная 8-12 40 18 000
2 Дровяная 10-16 48 19 500
3 Электрическая 9-15,5 15 15 000

Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6500 руб.

Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наименьшим для отопления помещений. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.

Из таблицы видно, что наименьший объем для первой печи — 8, для второй — 10, а для третьей — 9.

Найти радиус окружности печи

№ 5

Хозяин выбрал дровяную печь. Чертёж печи показан на рисунке. Размеры указаны в сантиметрах.

Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке по дуге окружности (см. рис.). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха показаны на рисунке. Найдите радиус в сантиметрах: ответ округлите до десятых.

[spoiler title=”источники:”]

http://math-oge.sdamgia.ru/problem?id=383595

http://remmeros.ru/matematika/234-dlya-ustanovki-pechki-khozyainu-ponadobilos-uznat-radius-zakrugleniya-arki-r.html

[/spoiler]

Источник

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

Радиус вписанной окружности в ромб

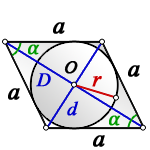
a – сторона ромба

D – большая диагональ

d – меньшая диагональ

α – острый угол

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула 1 радиуса вписанной окружности в ромб

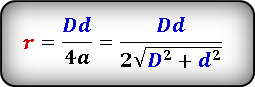
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула 2 радиуса вписанной окружности в ромб

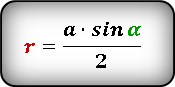
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула 3 радиуса вписанной окружности в ромб

Формула 4 радиуса вписанной окружности в ромб

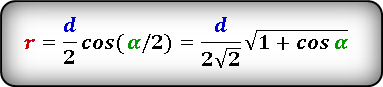
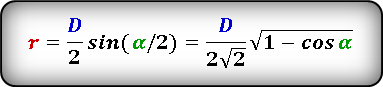
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

Формула 5 радиуса вписанной окружности в ромб

Формула 6 радиуса вписанной окружности в ромб

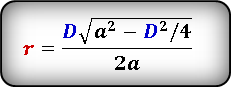
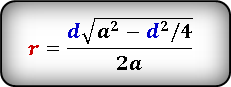
2. Радиус вписанной окружности ромба, равен половине его высоты

Радиус вписанной окружности в ромб

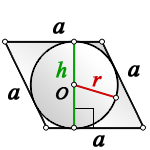
a – сторона ромба

h – высота

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Формула 7 радиуса вписанной окружности в ромб

Источник

Добавить комментарий