Нахождение радиуса круга: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса круга
1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:
C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2 π R
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:
S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:
S = π R 2
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать – как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Как посчитать радиус окружности
Онлайн калькулятор
Как посчитать радиус зная длину окружности
Чему равен радиус если длина окружности ?
Чему равен радиус (r) если длина окружности C?
Формула
r = C /2π , где π ≈ 3.14
Пример
Если длина круга равна 3 см, то его радиус примерно равен 0.477 см.
Как посчитать радиус окружности зная её площадь
Чему равен радиус окружности если
Чему равен радиус окружности (r) если её площадь S?
Формула
Пример
Если площадь круга равна 5 см 2 , то его радиус примерно равен 1.26 см.
Как посчитать радиус окружности зная диаметр
Чему равен радиус окружности если
Чему равен радиус окружности (r) если её диаметр d?
Формула
Пример
Если диаметр круга равен 3 см, то его радиус = 1.5 см.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
http://poschitat.online/radius-okruzhnosti
[/spoiler]
Все формулы ОГЭ 2023 по физике для 9 класса в удобном формате с пояснениями для успешной сдачи экзамена 24 мая 2023 года по каждой теме для решения задач и тренировочные варианты формата ОГЭ 2023.
- Скачать формулы №1
- Скачать формулы №2
- Скачать формулы №3
- Решать варианты ОГЭ 2023 по физике 9 класс
fizika_9klass_oge2023_formyli
Формулы ОГЭ 2023 по физике 9 класс состоят из следующих пунктов:
1. Скорость v = s/t, где v — скорость, s — расстояние, t — время.
2. Ускорение a = (v2 — v1)/t, где a — ускорение, v2 — конечная скорость, v1 — начальная скорость, t — время.
3. Закон сохранения энергии E1 + W = E2, где E1 — начальная энергия, W — работа, E2 — конечная энергия.
4. Мощность P = W/t, где P — мощность, W — работа, t — время.
5. Сила F = m*a, где F — сила, m — масса тела, a — ускорение.
6. Закон Архимеда FАрх = p*V*g, где FАрх — сила Архимеда, p — плотность жидкости, V — объем жидкости, g — ускорение свободного падения.
7. Закон Ома I = U/R, где I — сила тока, U — напряжение, R — сопротивление.
8. Закон Кулона F = k*q1*q2/r^2, где F — сила взаимодействия двух зарядов, k — постоянная Кулона, q1 и q2 — заряды тел, r — расстояние между зарядами.
9. Закон сохранения импульса p1 = p2, где p1 — начальный импульс, p2 — конечный импульс.
10. Закон Гука F = k*x, где F — сила, k — коэффициент жесткости пружины, x — деформация пружины.
Знание этих формул поможет ученикам подготовиться к ОГЭ по физике 9 класс и успешно справиться с заданиями на экзамене.
Экзамен будет состоять из заданий, проверяющих знания школьной программы по физике 9 класса, включая формулы и законы, а также умение решать задачи и анализировать экспериментальные данные. Ученикам рекомендуется тщательно подготовиться к экзамену, изучив весь курс физики и отработав навыки решения задач.
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Найти радиус и центростремительное ускорение, если известна скорость и период. Напишите формулы, пожалуйста.
Мастер
(1289),
закрыт
3 года назад
Владимир Александрович
Высший разум
(102904)
3 года назад
Найти радиус R и центростремительное ускорение a, если известна скорость V и период T. Напишите формулы, пожалуйста.
Период (Т) равен 0.05 с
Скорость (V) равна 15 м/с.
РЕШЕНИЕ:
Период Т это время полного оборота по кругу радиуса R. Его (круга) длина, с одной стороны: L = 2пR, с другой – L = V*T. Приравниваем: 2пR = V*T. Получаем:
R = V*T/(2п) = 15*0.05/(2*3,14) = 0,119 м.
Центростремительное ускорение: а = V²/R = V²/(V*T/(2п)) = 2пV/T = 2*3.14*15/0.05 = 1884 м/с².
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
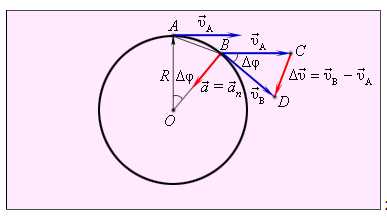
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
fizmat.by
Обозначения физических величин
Величины |
|
|
Наименование |
Обозначение |
Механические величины |
|
| Вес |
G, P, W |
| Время |
t |
| Высота |
h |
| Давление |
p |
| Диаметр |
d |
| Длина |
l |
| Длина пути |
s |
| Импульс (количество движения) |
p |
| Количество вещества |
ν, n |
| Коэффицент жесткости (жесткость) |
Ʀ |
| Коэффицент запаса прочности |
Ʀ, n |
| Коэффицент полезного действия |
η |
| Коэффицент трения качения |
Ʀ |
| Коэффицент трения скольжения |
μ, f |
| Масса |
m |
| Масса атома |
ma |
| Масса электрона |
me |
| Механическое напряжение |
σ |
| Модуль упругости (модуль Юнга) |
E |
| Момент силы |
M |
| Мощность |
P, N |
| Объем, вместимость |
V, ϑ |
| Период колебания |
T |
| Плотность |
ϱ |
| Площадь |
A, S |
| Поверхностное натяжение |
σ, γ |
| Постоянная гравитационная |
G |
| Предел прочности |
σпч |
| Работа |
W, A, L |
| Радиус |
r, R |
| Сила, сила тяжести |
F, Q, R |
| Скорость линейная |
ϑ |
| Скорость угловая |
ώ |
| Толщина |
d, δ |
| Ускорение линейное |
a |
| Ускорение свободного падения |
g |
| Частота |
ν, f |
| Частота вращения |
n |
| Ширина |
b |
| Энергия |
E, W |
| Энергия кинетитеская |
EƦ |
| Энергия потенциальная |
Ep |
|
|
| Длина волны | λ |
| Звуковая мощность |
P |
| Звуковая энергия |
W |
| Интенсивность звука |
I |
| Скорость звука |
c |
| Частота |
ν, f |
Тепловые величины и величины молекулярной физики |
|
| Абсолютная влажность |
a |
| Газовая постоянная (молярная) |
R |
| Количество теплоты |
Q |
| Коэффицент полезного действия |
η |
| Относительная влажность |
ϕ |
| Относительная молекулярная масса |
Mr |
| Постоянная (число) Авогадро |
NA |
| Постоянная Больцмана |
Ʀ |
| Постоянная (число) Лошмидта |
NL |
| Температура Кюри |
TC |
| Температура па шкале Цельсия |
t, ϴ |
| Температура термодинамическая (абсолютная температура) |
T |
| Температурный коэффицент линейного расширения |
a, ai |
| Температурный коффицент объемного расширения |
β, av |
| Удельная теплоемкость |
c |
| Удельная теплота парообразования |
r |
| Удельная теплота плавления |
λ |
| Удельная теплота сгорания топлива (сокращенно: теплота сгорания топлива) |
q |
| Число молекул |
N |
| Энергия внутренняя |
U |
Электрические и магнитные величины |
|
| Диэлектрическая проницаемость вакуума (электрическая постоянная) |
Ԑo |
| Индуктивность |
L |
| Коэффицент самоиндукции |
L |
| Коэффицент трансформации |
K |
| Магнитная индукция |
B |
| Магнитная проницаемость вакуума (магнитная постоянная) |
μo |
| Магнитный поток |
Ф |
| Мощность электрической цепи |
P |
| Напряженность магнитного поля |
H |
| Напряженность электрического поля |
E |
| Объемная плотность электрического заряда |
ϱ |
| Относительная диэлектрическая проницаемость |
Ԑr |
| Относительная магнитная проницаемость |
μr |
| Плотность эенгии магнитного поля удельная |
ωm |
| Плотность энергии электрического поля удельная |
ωэ |
| Плотность заряда поверхностная |
σ |
| Плотность электрического тока |
J |
| Постоянная (число) Фарадея |
F |
| Проницаемость диэлектрическая |
ԑ |
| Работа выхода электрона |
ϕ |
| Разность потенциалов |
U |
| Сила тока |
I |
| Температурный коэффицент электрического сопротивления |
a |
| Удельная электрическая проводимость |
γ |
| Удельное электрическое сопротивление |
ϱ |
| Частота электрического тока |
f, ν |
| Число виток обмотки |
N, ω |
| Электрическая емкость |
C |
| Электрическая индукция |
D |
| Электрическая проводимость |
G |
| Электрический момент диполя молекулы |
p |
| Электрический заряд (количество электричества) |
Q, q |
| Электрический потенциал |
V, ω |
| Электрическое напряжение |
U |
| Электрическое сопротивление |
R, r |
| Электродвижущая сила |
E, Ԑ |
| Электрохимический эквивалент |
Ʀ |
| Энергия магнитного поля |
Wm |
| Энергия электрического поля |
Wэ |
| Энергия Электромагнитная |
W |
Оптические величины |
|
| Длина волны |
λ |
| Освещенность |
E |
| Период колебания |
T |
| Плотность потока излучения |
Ф |
| Показатель (коэффицент) преломления |
n |
| Световой поток |
Ф |
| Светасила объектива |
f |
| Сила света |
I |
| Скорость света |
c |
| Увеличение линейное |
β |
| Увеличение окуляра, микроскопа, лупы |
Ѓ |
| Угол отражения луча |
έ |
| Угол падения луча |
ԑ |
| Фокусное расстояние |
F |
| Частота колебаний |
ν, f |
| Энергия излучения |
Q, W |
| Энергия световая |
Q |
Величины атомной физики |
|
| Атомная масса относительная |
Ar |
| Время полураспада |
T1/2 |
| Дефект массы |
Δ |
| Заряд электрона |
e |
| Масса атома |
ma |
| Масса нейтрона |
mn |
| Масса протона |
mp |
| Масса электрона |
me |
| Постоянная Планка |
h, ħ |
| Радиус электрона |
re |
Величины ионизирующих излучений |
|
| Поглощеная доза излучения (доза излучения) |
D |
| Мощность поглощенной дозы излучения |
Ď |
| Активность нуклида в радиоактивном источнике |
A |
www.kilomol.ru
Радиус кривизны траектории
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1. Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.
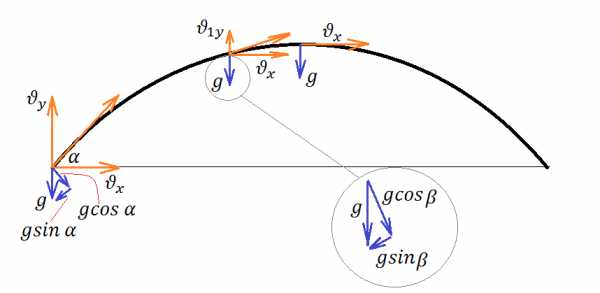
К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м, м, м.
Задача 2. Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и :
Откуда .
Ответ: а) , б) .
easy-physic.ru
Чему равен радиус земли? Нужно для решения задачи по физике.
в районе 6500 км.
Двум лунным меридианам.
Примерно 6.000 км
Полярный радиус 6356 км. Экваториальный радиус 6378 км. 40.075 км радиус Земли
touch.otvet.mail.ru
напишите формулу радиуса круга по физике.
Радиус круга изучают в математике, а не в физике, бл…
S = πR^2 — отсюда R = корень из выражения S/π
<a href=»/» rel=»nofollow» title=»4078963:##:otvety/thread?tid=6c645576ab6a24c0″>[ссылка заблокирована по решению администрации проекта]</a> посмотри
Если по физике, то решив несложное уравнение Шредингера мы получим четыре третьих пи эр в кубе (это если волновая функция ФИ равна одной второй) Про интегралы в следующих вопросах.
touch.otvet.mail.ru
Боровский радиус | Все формулы
Боровский радиус — радиус ближайшей к ядру орбиты электрона атома водорода в модели атома
Боровский радиус часто используется в атомной физике в качестве атомной единицы длины. Определение Боровского радиуса включает не приведённую, а обыкновенную массу электрона и, таким образом, радиус Бора не точно равен радиусу орбиты электрона в атоме водорода. Это сделано для удобства: Боровский радиус в таком виде возникает в уравнениях, описывающих и другие атомы, где выражение для приведённой массы отлично от атома водорода
В формуле мы использовали :
— Боровский радиус
[Дж*с] — Постоянная планка
[Кг] — Масса электрона
— Постоянная тонкой структуры
— Скорость света в вакууме
xn--b1agsdjmeuf9e.xn--p1ai
Боровский радиус – Формулы по физике.рф
Боровский радиус — радиус ближайшей к ядру орбиты электрона атома водорода в модели атома
Боровский радиус часто используется в атомной физике в качестве атомной единицы длины. Определение Боровского радиуса включает не приведённую, а обыкновенную массу электрона и, таким образом, радиус Бора не точно равен радиусу орбиты электрона в атоме водорода. Это сделано для удобства: Боровский радиус в таком виде возникает в уравнениях, описывающих и другие атомы, где выражение для приведённой массы отлично от атома водорода
В формуле мы использовали :
— Боровский радиус
[Дж*с] — Постоянная планка
[Кг] — Масса электрона
— Постоянная тонкой структуры
— Скорость света в вакууме
xn--e1adcbkcgpcji1bjh6h.xn--p1ai
Кинематика
Динамика
- Силы трения
- Трение покоя
Максимальная сила трения покоя (Fтр)max пропорциональна силе нормального давления (N) и зависит от характера взаимодействия соприкасающихся поверхностей тел, определяемого коэффициентом трения (μ)
(Fтр)max=μ×N
СИ: Н - Трение скольжения
Сила трения скольжения (Fтр) пропорциональна силе давления (N), коэффициенту трения (μ) и направлена противоположно направлению движения тела.
Fтр=μ×N
СИ: Н - Коэффициент трения
Коэффициент трения (μ) вычисляют как отношение модулей силы трения (Fтр) и силы давления (N).
μ=Fтр/N - Движение тела под действием силы трения
1) Путь (l), пройденный движущимся телом под действием силы трения до полной остановки (тормозной путь), прямо пропорционален квадрату начальной скорости (v0) и обратно пропорционален коэффициенту трения (μ):
, (g — ускорение свободного падения).
2) Время (t) движения тела под действием силы трения до момента полной остановки (время торможения) прямо пропорционально начальной скорости (v0) и обратно пропорционально коэффициенту трения (μ):
СИ: м, с
, (g — ускорение свободного падения).
- Движение тела под действием нескольких сил
- Условие равновесия тела (как материальной точки).
Тело находится в равновесии (в покое или движется равномерно и прямолинейно), если сумма проекций всех сил (), действующих на тело, на любую ось (ОХ, ОY, O, …) равна нулю.
;
;
СИ: Н - Движение тела по наклонной плоскости
Ускорение тела, скользящего вниз по наклонной плоскости с углом наклона (α) и коэффициентом трения тела о плоскость (μ), не зависит от массы тела и равно:, (g — ускорение свободного падения)
СИ: м/с2 - Движение связанных тел через неподвижный блок
Ускорение двух тел, массами m1 и m2, связанных нитью, перекинутой через неподвижный блок, равно:
, (g — ускорение свободного падения)
СИ: м/с2
), действующих на тело, на любую ось (ОХ, ОY, O, …) равна нулю.
;
;
, (g — ускорение свободного падения)
, (g — ускорение свободного падения)- Законы сохранения в механике
- Импульс тела
Импульс тела () — векторная величина, равная произведению массы (m) тела на его скорость ().
СИ: (кг×м)/с - Импульс силы
Импульс силы ( — произведение силы на время t её действия) равен изменению импульса тела.
СИ: Н×с - Закон сохранения импульса
Геометрическая сумма импульсов тел (), составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
СИ: Н×с - Механическая работа силы
Работа (А) постоянной силы равна произведению модулей векторов силы () и перемещения () на косинус угла между этими векторами.
СИ: Дж - Теорема о кинетической энергии
Работа (А) силы (или равнодействующей сил) равна изменению кинетической энергии (Ek1 и Ek2) движущегося тела.
,
где m — масса тела, v1, v2 — начальная и конечная скорости тела
СИ: Дж - Потенциальная энергия поднятого тела
Потенциальная энергия (ЕП) тела, поднятого на некоторую высоту (h) над нулевым уровнем, равна работе (А) силы тяжести (m×g) при падении тела с этой высоты до нулевого уровня.
A=ЕП=m×g×h
СИ: Дж - Работа силы тяжести
Работа (А) силы тяжести (mg) не зависит от пути, пройденного телом, а определяется разностью высот (Δh=h2-h1) положения тела в конце и в начале пути и равна разности его потенциальных энергий (EП2 и EП1).
A=-(EП2-EП1)=-m×g×Δh
СИ: Дж - Потенциальная энергия деформированного тела
Потенциальная энергия (ЕП) деформированного тела (пружины) равна работе силы упругости при переходе тела (пружины) в состояние, в котором его деформация равна нулю.
ЕП =,
где k — жесткость; х — деформация пружины.
СИ: Дж - Закон сохранения полной механической энергии
Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.
ЕК2+ЕП2=ЕК1+ЕП1=const
СИ: Дж
) — векторная величина, равная произведению массы (m) тела на его скорость (
).
— произведение силы 
на время t её действия) равен изменению импульса тела.
), составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
) на косинус угла между этими векторами.
,
,- Движение жидкостей и газов по трубам
- Закон Бернулли
Давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость её движения меньше, и наоборот, в тех частях, где скорость больше, давление меньше.
,
где p1, v1, h1 — давление, скорость и вертикальная координата жидкости в одном сечении трубы; p2, v2, h2 — давление, скорость и вертикальная координата жидкости в другом сечении трубы;
ρ — плотность жидкости; g — ускорение свободного падения.
СИ: Па
,
