Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
![]()
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
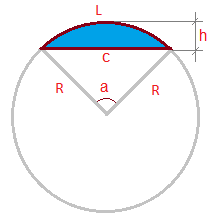
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.
 Сегмент круга
Сегмент круга
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Вычислить радиус окружности по сегменту
Радиус и высота сегмента круга

Свойства
Зная радиус и высоту сегмента, можно найти центральный угол α, через который становится возможным рассчитать все остальные измерения сегмента, такие как длина дуги, длина хорды и площадь сегмента круга. Из формулы высоты следует, что косинус половинного угла равен разности единицы и отношения высоты к радиусу. cos〖α/2〗=1-h/r
Вычислив таким образом центральный угол сегмента круга, подставляем его в следующие формулы для длины дуги и длины хорды. Длина дуги вычисляется как произведение угла на радиус, а длина хорды находится из прямоугольного треугольника как удвоенное произведение радиуса на синус половинного угла (рис.141). P=αr c=2r sin〖α/2〗
Площадь сегмента круга наряду с площадью равнобедренного треугольника, образованного двумя радиусами и хордой, является составляющей площади сектора круга. Поэтому, чтобы найти площадь сегмента необходимо вычесть из последней площадь треугольника. Упростив такое выражение, получаем половину квадрата радиуса, умноженную на разность угла α и его синуса. S=S_сек-S_тр=(r^2 α)/2-r^2 sinα=1/2 r^2 (α-sinα )
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.
 Сегмент круга
Сегмент круга
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Как определить радиус дуги или сегмента круга и найти центр
Иногда, при выполнении особо заковыристых работ по отделке приходится решать не совсем простые задачи. Например, имеется часть окружности, говоря по научному — дуга и для этой дуги нужно определить радиус и найти центр окружности.
Сделать это можно двумя методами. Первый метод основан на расчетах, а второй — прикладной. Сначала рассмотрим первый метод, его достоинства и недостатки, а затем второй.
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки», поэтому здесь лишь приведу основные формулы:
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад — для того, чтобы напомнить формулы — есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше — то искомый центр дуги выше на прямой.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Категории:
- Расчет конструкций . Основы прикладной геометрии
Оценка пользователей:
8.5 (голосов: 2)
Переходов на сайт:
31889
Комментарии:
R = H/(1 — cos(a/2))
Радиус прямо пропорционален H.
Как так?
Я достаточно подробно ответил на ваш вопрос в статье «Расчет арочной перемычки», где вы задали подобный вопрос.
Если угол не нужен для дальнейших расчетов, радиус находится проще — без тригонометрических функций и даже можно без калькулятора — на бумажке. R = L^2/(8*H) + H/2
Сначала термины:
Отрезок, соединяющий концы дуги называется хордой (a), а высота сегмента (перпендикуляр из середины хорды) — стрелкой (h).
Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. То есть R^2=(R-h)^2+(a/2)^2.
А что касается нахождения центра, то перпендикуляры к серединам хорд пересекаются в центре!
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Радиус и высота сегмента круга

Свойства
Зная радиус и высоту сегмента, можно найти центральный угол α, через который становится возможным рассчитать все остальные измерения сегмента, такие как длина дуги, длина хорды и площадь сегмента круга. Из формулы высоты следует, что косинус половинного угла равен разности единицы и отношения высоты к радиусу. cos〖α/2〗=1-h/r
Вычислив таким образом центральный угол сегмента круга, подставляем его в следующие формулы для длины дуги и длины хорды. Длина дуги вычисляется как произведение угла на радиус, а длина хорды находится из прямоугольного треугольника как удвоенное произведение радиуса на синус половинного угла (рис.141). P=αr c=2r sin〖α/2〗
Площадь сегмента круга наряду с площадью равнобедренного треугольника, образованного двумя радиусами и хордой, является составляющей площади сектора круга. Поэтому, чтобы найти площадь сегмента необходимо вычесть из последней площадь треугольника. Упростив такое выражение, получаем половину квадрата радиуса, умноженную на разность угла α и его синуса. S=S_сек-S_тр=(r^2 α)/2-r^2 sinα=1/2 r^2 (α-sinα )
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/vychislit-radius-okruzhnosti-po-segmentu
http://geleot.ru/education/math/geometry/calc/circular_segment/radius_and_height
[/spoiler]
Зная радиус и высоту сегмента, можно найти центральный угол α, через который становится возможным рассчитать все остальные измерения сегмента, такие как длина дуги, длина хорды и площадь сегмента круга. Из формулы высоты следует, что косинус половинного угла равен разности единицы и отношения высоты к радиусу.
cos〖α/2〗=1-h/r
Вычислив таким образом центральный угол сегмента круга, подставляем его в следующие формулы для длины дуги и длины хорды. Длина дуги вычисляется как произведение угла на радиус, а длина хорды находится из прямоугольного треугольника как удвоенное произведение радиуса на синус половинного угла (рис.141).
P=αr
c=2r sin〖α/2〗
Площадь сегмента круга наряду с площадью равнобедренного треугольника, образованного двумя радиусами и хордой, является составляющей площади сектора круга. Поэтому, чтобы найти площадь сегмента необходимо вычесть из последней площадь треугольника. Упростив такое выражение, получаем половину квадрата радиуса, умноженную на разность угла α и его синуса.
S=S_сек-S_тр=(r^2 α)/2-r^2 sinα=1/2 r^2 (α-sinα )
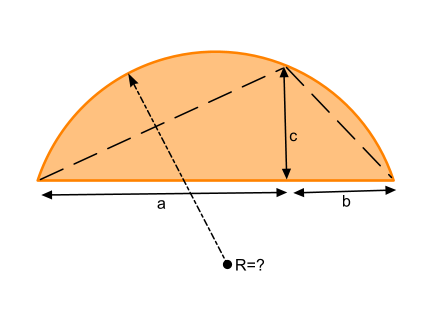
По сегменту определить радиус окружности
Небольшой калькулятор, который позволит нам тремя измерениями заданного сегмента круга определить его радиус
Вам нужно всего три измерения и два/один инструмент: линейка +уголок(что бы отмерить прямой угол)
Итак, у вас есть неизвестный сегмент круга и вы измерили три значения (a,b,c)
Соединим точки на окружности между собой (пунктирная линия). Мы получили треугольник, с высотой (c) и общим основанием (a+b)
Этот треугольник оказывается вписанным в окружность, а мы знаем связь между площадью треугольника, его сторонами (p, q, m) и описанной окружностью радиусом (R)
(S=cfrac{pqm}{4R})
Тогда (R=cfrac{pqm}{4S})
Одна сторона нам известна (a+b)
две другие мы найдем по теореме Пифагора (sqrt{a^2+c^2}) и (sqrt{b^2+c^2})
Осталось решить что же делать с площадью
Вспомним, что площадь треугольника равна половине произведения основания треугольника на его высоту
(S=cfrac{(a+b)c}{2})
подставим все найденные выражения и получим
(R=cfrac{sqrt{a^2+c^2}sqrt{b^2+c^2}}{2c})
Если бы мы выбрали (a) и (b) равными то получили бы
(R=cfrac{{a^2+c^2}}{2c})
где (с) – уже являлась бы высотой сегмента.
Сегмент круга
Данный калькулятор считает параметры сегмента круга, а именно:
- длину дуги (L),
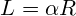
- длину хорды (C),
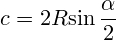
- площадь (S),
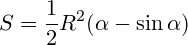
- высоту (h),
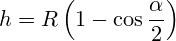
Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:
1) сегмент круга решается с помощью радиуса (R) и угла (A).
2) сегмент круга находим с помощью высоты и длины хорды.
Однако, как справедливо заметил наш пользователь:“на практике hourто случается, что как радиус дуги, так и угол неизвестны” (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента, вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу: