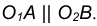Сопряжения в инженерной графике на чертежах с примерами
Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
Точка касания К и центры окружностей
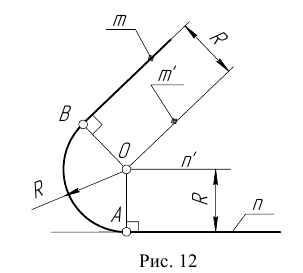
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 
Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 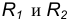
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 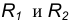
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Построение касательных
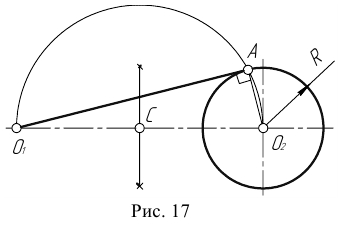
Пример 1. Дана окружность с центром в точке 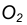
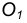
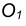
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 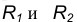
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Окружность
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ 
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.
Хорда AB стягивает дуги 

Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать – как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://izamorfix.ru/matematika/planimetriya/okruzhnost.html
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
[/spoiler]
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а)2 + (у – b)2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
Пример №1:
(х – 1)2 + (у – 2)2 = 42
Найдем центр окружности:
х – 1=0
x=1
у – 2=0
y=2
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2=4
R 2=22
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.
Пример №2:
х2 + (у + 1)2 =1
Можно представить уравнение окружности ввиде:
(х-0)2 + (у + 1)2 =12
Найдем центр окружности:
х=0
у + 1=0
y=–1
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2=1
R 2=12
R=1
Построим окружность.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Окружность — геометрическая фигура, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от данной точки.
Эту точку называют центром окружности, а заданное расстояние — радиусом окружности.
Радиус — это отрезок, соединяющий центр окружности с любой точкой окружности. Из определения следует, что можно провести бесконечное количество радиусов, и они все имеют одинаковую длину.
Отрезок, который соединяет две точки на окружности, называют хордой.
Если хорда проходит через центр окружности, то её называют диаметром окружности.
Диаметр — самая длинная хорда.
В окружности также можно провести бесконечное количество диаметров.
Если соединить две точки окружности не отрезком, а кривой, проходящей по самой окружности, то часть окружности между двумя точками называют дугой.
Если на окружности отметить две точки, то получаются две дуги. Поэтому для названия дуги используют три латинские буквы, которые могут быть как маленькие, так и большие.
На рисунке выше можем назвать: дуга (BDH), дуга (ACG) и другие.
На рисунке ниже нарисованы: дуга (AxB) и дуга (AyB).
Часть плоскости, ограниченная окружностью, называется кругом.
В задачах, где необходимо выполнить конструкции, используются циркуль и линейка.
Очень важно запомнить, что в этих задачах линейка используется не как инструмент для измерения, а исключительно только для того, чтобы провести прямую, луч или отрезок через две данные точки, то есть, чтобы провести прямую линию. Циркуль используется для построения окружности или дуги окружности.
Рассмотрим пять основных построений, в которых используем упомянутые действия — построение прямой линии и окружности.
1. На данном луче от его начала отложить отрезок, равный данному.
2. Построение угла, равного данному.
3. Построение биссектрисы угла.
4. Построение перпендикулярных прямых.
5. Построение середины отрезка.
1. На данном луче от его начала отложить отрезок, равный данному.
См. видео.
Ясно, что таким образом мы получили отрезок, равный данному. Соответственно определению окружности, она состоит из точек, расположенных на заданном расстоянии (радиусе) от некоей точки (центра окружности).
Если центром служит начальная точка луча (C), радиусом — данный отрезок (AB), то точка пересечения окружности и луча (D) и есть искомая конечная точка отрезка (CD), равного данному отрезку (AB).
2. Построение угла, равного данному.
См. видео.
Докажем, что построенный угол (ECD) и есть тот искомый угол, равный данному углу (AOB).
Если мы построили окружность с центром (C) — начальной точкой луча и таким же радиусом, как у окружности с центром (O), то (CD) (=) (OB).
Если далее мы построили окружность с центром (D) и радиусом, равным отрезку (BA), и получили точку пересечения обеих окружностей (E), то (BA) (=) (DE).
Провели луч (CE). Очевидно, (OA) (=) (CE).
Значит, треугольники (AOB) и (ECD) равны по третьему признаку равенства треугольников, у них равны и углы, в том числе угол (ECD) равен углу (AOB).
3. Построение биссектрисы угла.
См. видео.
Чтобы доказать, что (OC) действительно делит угол (AOB) пополам, достаточно рассмотреть треугольники (AOC) и (BOC).
(OA = OB) как радиусы одной окружности, а (AC = BC), так как мы при построении выбрали одинаковые радиусы для обеих окружностей.
Сторона (OC) — общая.
Эти треугольники равны по третьему признаку.
Следовательно, их соответствующие углы равны.
Значит, (AOC) и (BOC) — две равные части одного угла, это означает, что луч (OC) делит угол пополам.
4. Построение перпендикулярных прямых.
См. видео.
Почему (DE) является перпендикулярной к (BC)?
(AB = AC) — так эти точки были отложены при построении.
(BD = CD), так как мы обе окружности построили с одинаковыми радиусами.
Значит, (DA) или (EA) — медианы, проведённые к основанию равнобедренных треугольников (BDC) или (BEC).
Медиана в равнобедренном треугольнике является также высотой, то есть перпендикулярна к основанию.
5. Построение середины отрезка.
См. видео.
Эта конструкция такая же, как в случае построения перпендикулярных прямых, и уже доказано, что (DC) или (EC) делит (AB) пополам, то есть (C) — серединная точка отрезка (AB).
Окружность
- Построение окружности циркулем
- Радиус, хорда и диаметр
- Дуга
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
D = 2r.
Дуга
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ 
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.
Хорда AB стягивает дуги 

|
Встретил забавную задачу и приглашаю многоуважаемую публику ей поразвлечься… ) Есть окружность. Внутри окружности проведена хорда a, от одного из концов этой хорды проведен внутри окружности под прямым углом отрезок b так, что он не пересекает и не касается окружности. От второго конца отрезка b опять же, под прямым углом, проведен отрезок с, который вторым концом касается окружности. Длина всех отрезков больше нуля. Отрезки a и с лежат в разных полуплоскостях относительно прямой, проходящей через отрезок b. Я не знаю, вроде все по условиям, все как на картинке, честное слово! Мы знаем длины a, b и c. Нужно найти радиус окружности. Можно воспользоваться свойствами хорды, готовыми уравнениями. Точка пересечения двух хорд делит обе хорды в одинаковом соотношении. Используем эту формулу для нахождения отрезка d (cм. рисунок). Когда хорды перпендикулярны то радиус окружности находится по второй формуле. автор вопроса выбрал этот ответ лучшим Тут вспомнил, как мне один раз на практике нужно было найти радиус окружности и были три точки.. Сделано это было простым графическим методом без всяких заумностей.. Просто известно, что радиус в каждой точке окружности перпендикулярен касательной к окружности (которая есть суть производной, но это так, к слову).. Далее, известно, что хорда всегда идёт параллельно касательной (собственно касательная – это хорда сдвинутая на край окружности и касающаяся её в одной точке).. Вот и всё, что нужно.. Без матриц, определителей, систем уравнений, хитроумных формул и построений.. Итак, вот рисунок.. Т. е., мы просто достроили ещё одну хорду (красным цветом), затем каждую хорду поделили пополам и из середины каждой хорды провели линии, перпендикулярные хорде.. Точка пересечения двух линий, перпендикулярных хордам и есть центр окружности.. Теперь из цента мы ставим ногу циркуля и рисуем окружность (можно использовать карандаш на нитке (как пришлось использовать на практике).. Также для построения перпендикуляров использовалась нитка и древний способ построения перпендикуляров.. Деление напополам: сложение отмеренной нитки вдвое.. Всё делается на коленке.. И даже можно использовать на местности для построения окружностей в масштабах сотен метров и более.. Т.е. мы нашли не только радиус, но даже центр окружности и при желании можем с помощью циркуля (или карандаша на нитке) построить искомую окружность.. Именно так на практике мне один раз пришлось искать окружность, причём нужно было знать не только радиус, но расположение центра.. Этот метод наиболее прост, универсален и с помощью его можно искать все параметры окружности.. Если нужно найти радиус с наперёд заданной точностью, то можно использовать метод в моём предыдущем ответе, решение системы из трёх квадратных уравнений, которые описывают нахождение трёх точек, можно решать их не обязательно аналитически, что немного трудоёмко (но не сложно), а используя тот же Маткад.. Кроме того этот аналитический метод может помочь определить не только радиус окружности, но и координаты центра с любой заданной точностью, т.е. все параметры окружности.. Кстати, посткриптум, этот графический метод пришлось придумывать на ходу, поскольку нужно было срочно найти ответ, искать что-то в литературе как найти окружность просто не было времени.. Конечно хорошо знать определитель, которым задаётся дуга окружности через 3 точки.. Как это написал Гр. Роджер.. Можно сделать хитроумные геометрические построения, как сделал родиоил2.. Можно использовать свойства дуги, как попытался это сделать мсб.. Но вот, положим вам на практике нужно быстро определить, тогда нужно искать свойства дуг, определителей?.. Или пыхтеть с построениями? Которые могут быть не очень точны из-за несовершенства инструментария.. Как же поступить? Да как на войне: быстро и эффективно, используя смекалку и минимум средств.. Воспользуемся простыми формулами, которые известны из школы.. И элементами аналитической геометрии (опять это практически школа).. Известно, что уравнение окружности: (x-xo)^2+(y-yo)^2=R^2 где xo, y0, R – соответственно координаты центра и радиус окружности.. Установим первую точку А так, чтобы она находилась в начале координат А(0,0), тогда следующая точка В имеет координаты (0,а), следующая точка С (b, c+a).. Теперь напишем три уравнения одной и той же окружности для трёх точек: (xo)^2+(yo)^2=R^2 (xo)^2+(а-yo)^2=R^2 (b-xo)^2+(с+а-yo)^2=R^2 Получилась система из трёх квадратных уравнений с тремя неизвестными: xo, y0, R.. Значит эта система вполне решается стандартным образом.. Например приравниваем первое и второе уравнение: (xo)^2+(yo)^2=(xo)^2+(а-yo)^2 Тогда всё приводится к уравнению: (yo)^2-(а-yo)^2=0 Упрощаем его и получаем простое линейное уравнение: -2ay0-(а)^2=0 y0=-(а)^2/2a=-a/2 Из него находим первую координату центра.. Затем эту координату подставляем в первое уравнение (которое попроще): (xo)^2+(a/2)^2=R^2 x0=+(-)sqrt(R^2-(a/2)^2) Теперь координаты центра подставляем опять в третье уравнение: (b-R^2-(a/2)^2)^2+(с+а+a/2)^2=R^2 Далее всё приводим, раскрывая скобки, получая уравнение 4-й степени.. Не в каждой школе дают решение уравнения 4-й степени, но это не сложно используя метод Феррари или метод разложения на множетели.. Грустный Роджер 2 года назад Это трёхходовка на аналитическую геометрию. Я расскажу, как она решается, но вычисления вы уж проведите сами… Будем считать, что длины всех трёх отрезков нам известны, и будем для простоты считать, что начало координат находится в точке сопряжения отрезков a, b. Тогда нижний конец отрезка а находится в точке (0, -А) (пусть заглавная буква – это длина соответствующего отрезка), а верхний конец отрезка с находится в точке (В, С). И тогда уравнение окружности, проходящей через три точки с известными координатами, пишется фактически “в одно действие” – через определитель, составленный из координат трёх точек, через которые она проходит: По счастью, при сделанном выше выборе осей координат одна строка определителя получается почти нулевой, и тогда он элементарно превращается в определитель третьего порядка (если знать, что такое минор): Тут, если совсем формально, перед определителем 3 порядка должен стоять минус, но поскольу он равен нулю, то фиг с ним, с минусом… Ну так вот. “Каноническое” уравнение окружности в декартовой системе координат выглядит так: x² + y² + Mx + Ny + K = 0. Если раскрыть определитель, то приравниванием коэффициентов при соответствующих степенях х, у враз получаются выражения для M, N и К. Ну а как только эти величины известны, радиус вычисляется как корень из (M² + N² – 4C). rodleoil2 2 года назад Предлагаю графическое решение Оно поможет найти и математическое решение Чертим линии а,б,с, соблюдая размеры и углы. Чертим одинаковые окружности, чтобы они попарно (одинакового размера рядом) пересекались. на данном чертеже все окружности одинаковые (размеры позволяют). Оранжевые окружности. Проводим линии через пересечения окружностей. Зеленые тонкие линии. Расстояния от точек соприкосновения заданных отрезков “а”, “б”, а также концов отрезков “а” и “с” и тонких зеленых линий будет радиусом Толстые зеленые линии. Также, легко заметить, что мы проводили тонкие зеленые линии – это серединные перпендикуляры к хордам. При необходимости, математическое решение можно получить работая с размерами отрезков, треугольниками, углами… Но на практике, на чертежах, хватает и графического решения. Грустный Роджер 2 года назад (Продолжение банкета…) Ответ msb натолкнул на забавную мысль: если нужно решить задачу графически, чисто циркулем и линейкой, то хорды b, c вообще на фиг не нужны, потому что есть окружность (это, заметьте, по условию задачки!) и есть хорда в ней. Всё, sapienti sat. На окружности строится ещё одна хорда, лежащая точно напротив хорды а, это делается циркулем и линейкой (проводятся два перпендикуляра к концам отрезка, фигня вопрос…), это нам даёт прямоугольник, вписанный в окружность. Собсно, всё, радиус отсюда определяется на раз. Но и это ещё не конец! Можно не строить этот прямоугольник. Можно построить два перпендикуляра – один к середине хорды a, второй – к середине отрезка, образованного лежащими на окружности концами хорд b, c. Точка их пересечения даст центр окружности. Никольский 2 года назад Фигура АВСD – описанная равнобедренная трапеция (см. рисунок), где а – верхнее основание трапеции, f – нижнее основание трапеции, k – боковая сторона трапеции, m – диагональ трапеции. k и m вычисляются из прямоугольных треугольников, f=2с + а Р – полупериметр треугольника АСD. Р = (m + k + f)/2 Есть формула, по которой вычисляется радиус окружности описанной равнобедренной трапеции: R = (kmf)/(4(sqrt(P(P-k)(P-m)(P-f))) Выражая k, m, f через а, в, с, получим (даже не буду пытаться) конечную формулу. Если знать конкретные числовые значения а, в, с, то найти R можно с помощью калькулятора. Геометрические задачи решаются графически. Здесь много лишних данных. Достаточно продлить отрезок b до пересечения с окружностью и соединить линией эту точку пересечения с точкой пересечения отрезка a c окружностью. Это будет диаметр окружности, который только остается разделить пополам с помощью циркуля и линейки и измерить. Знаете ответ? |
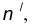 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.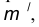 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.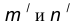 найдем центр сопряжения О.
найдем центр сопряжения О.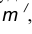 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.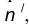 проведенная радиусом
проведенная радиусом 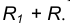
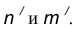
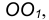 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.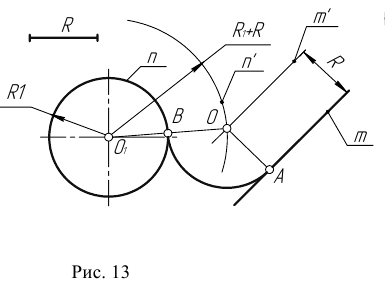
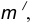 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 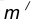 равен
равен 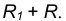
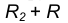 проведем окружность
проведем окружность 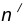 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.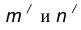 .
.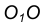 с дугой m.
с дугой m.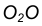 с дугой n .
с дугой n .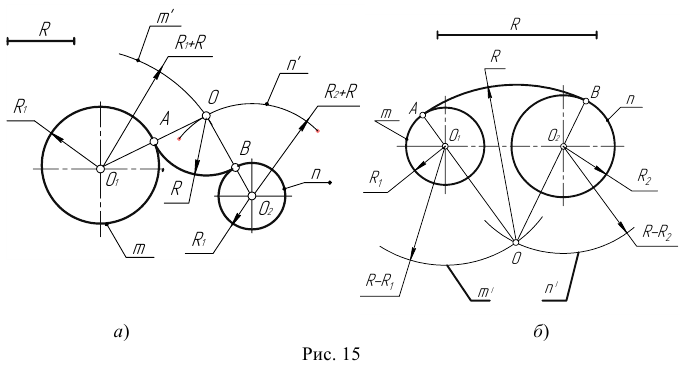
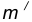 на расстоянии
на расстоянии  от данной окружности m.
от данной окружности m. на расстоянии
на расстоянии 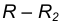 от данной окружности n.
от данной окружности n.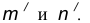
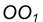 с заданной окружностью m.
с заданной окружностью m.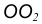 c заданной окружностью n.
c заданной окружностью n.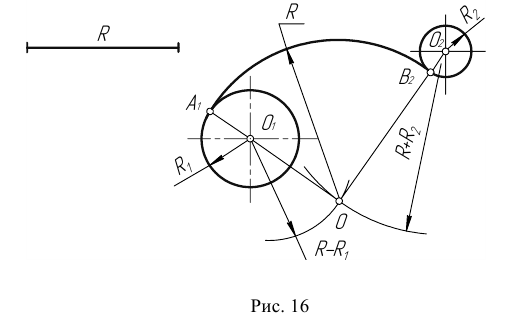
 с центром окружности
с центром окружности 
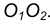
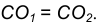
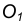 с точкой А.
с точкой А.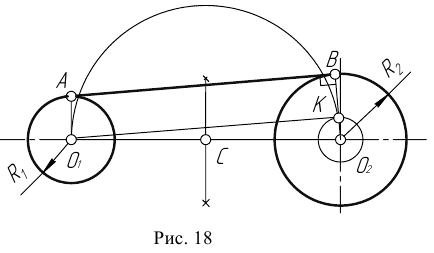
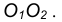
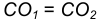 проведем вспомогательную окружность.
проведем вспомогательную окружность.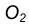 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 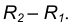
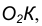 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем