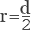Как посчитать радиус окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать радиус окружности
Чтобы посчитать радиус окружности (круга) воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Как посчитать радиус зная длину окружности
Чему равен радиус если длина окружности ?
Ответ:
0
Чему равен радиус (r) если длина окружности C?
Формула
r = C/2π, где π ≈ 3.14
Пример
Если длина круга равна 3 см, то его радиус примерно равен 0.477 см.
Как посчитать радиус окружности зная её площадь
Чему равен радиус окружности если
её площадь ?
Ответ:
0
Чему равен радиус окружности (r) если её площадь S?
Формула
r = √S/π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см2, то его радиус примерно равен 1.26 см.
Как посчитать радиус окружности зная диаметр
Чему равен радиус окружности если
её диаметр ?
Ответ:
0
Чему равен радиус окружности (r) если её диаметр d?
Формула
r = d/2
Пример
Если диаметр круга равен 3 см, то его радиус = 1.5 см.
См. также
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
При помощи нашего калькулятора вы легко сможете узнать радиус круга или окружности.
Для того что бы вычислить радиус круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить радиус круга.
Радиус круга рассчитывается по следующим формулам:
- Если нам известна длина:
Формула для расчета радиуса круга через его длину:
R=P/(2π) - Если нам известна площадь:
Формула для расчета радиус круга через площадь:
R=√
S/π
- Если нам известен диаметр:
Формула для расчета радиус круга через диаметр:
R=D/2
Где R – радиус круга, S – площадь круга, P – длина круга, D – диаметр, π – число Пи которое всегда примерно равно 3,14.
Радиус круга (окружности) – отрезок, который соединяет центр плоской геометрической фигуры с ее граничной линией. Онлайн калькулятор позволяет найти радиус круга по исходному значению длины окружности.
Размер любой окружности зависит от одного единственного параметра, которым руководствуются при ее начертании – это радиус. Радиус окружности по определению является расстоянием от центра окружности до каждой точки, находящейся на ней. Радиус окружности находится в прямо пропорциональной зависимости от длины окружности и диаметра. Радиус окружностей, вписанных и описанных вокруг многоугольников, также связан и с другими измерениями.

Радиус круга представляет собой равноудаленность всех точек окружности от ее центра. Вне зависимости от размера окружности, радиус представляет собой отношение длины окружности к удвоенному числу π, приблизительно равному 3,14. 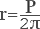
Также значение радиуса можно рассчитать, опираясь на площадь круга. Для этого надо извлечь квадратный корень из отношения площади круга к числу π. 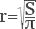
Самый простой способ определит радиус круга – через диаметр. Диаметр является удвоенным радиусом, значит, для нахождения радиуса нужно диаметр разделить на два:
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Найти радиус если длина окружности 10п
Как посчитать радиус окружности
Онлайн калькулятор
Как посчитать радиус зная длину окружности
Чему равен радиус если длина окружности ?
Чему равен радиус (r) если длина окружности C?
Формула
r = C /2π , где π ≈ 3.14
Пример
Если длина круга равна 3 см, то его радиус примерно равен 0.477 см.
Как посчитать радиус окружности зная её площадь
Чему равен радиус окружности если
Чему равен радиус окружности (r) если её площадь S?
Формула
Пример
Если площадь круга равна 5 см 2 , то его радиус примерно равен 1.26 см.
Как посчитать радиус окружности зная диаметр
Чему равен радиус окружности если
Чему равен радиус окружности (r) если её диаметр d?
Формула
Пример
Если диаметр круга равен 3 см, то его радиус = 1.5 см.
Радиус — что это такое и как найти радиус окружности
Через длину стороны
Формула для нахождения длины окружности через радиус:
, где r — радиус окружности.
Найти радиус круга, зная окружность
Окружность круга P
Результат
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Длина диаметра равна удвоенной длине радиуса.
Вычисление радиуса
Радиус можно посчитать разными способами.
Если известен диаметр
Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.
Если известна длина окружности круга
Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:
Означает данное значение отношение длины окружности к диаметру той же окружности.
Если известна площадь круга
Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:
В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.
Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.
Способ расчета радиуса круга:
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Как посчитать радиус зная длину окружности
Чему равен радиус (r) если длина окружности C?
Формула
r = C /2π , где π ≈ 3.14
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
По площади сектора и центральному углу
- Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем
В случае, когда величина α выражена в в радианах , получаем
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Центральный угол, вписанный угол и их свойства
Связанные определения
- Центральный угол в окружности — это угол , образованный двумя радиусами.
- Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .
В случае, когда величина α выражена в градусах , справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах , справедлива пропорция
из которой вытекает равенство:
Уравнение окружности
r 2 = ( x – a ) 2 + ( y – b ) 2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
Длина окружности равна 10 пи найдите радиус окружности
Вопрос по математике:
Найдите радиус окружности, длина которой равна 10п см
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 2
2πr = 10π
10π/2/π=r
10π/2/π=5
r – радиус
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат – это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи – смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Как посчитать радиус окружности
Онлайн калькулятор
Как посчитать радиус зная длину окружности
Чему равен радиус если длина окружности ?
Чему равен радиус (r) если длина окружности C?
Формула
r = C /2π , где π ≈ 3.14
Пример
Если длина круга равна 3 см, то его радиус примерно равен 0.477 см.
Как посчитать радиус окружности зная её площадь
Чему равен радиус окружности если
Чему равен радиус окружности (r) если её площадь S?
Формула
Пример
Если площадь круга равна 5 см 2 , то его радиус примерно равен 1.26 см.
Как посчитать радиус окружности зная диаметр
Чему равен радиус окружности если
Чему равен радиус окружности (r) если её диаметр d?
Формула
Пример
Если диаметр круга равен 3 см, то его радиус = 1.5 см.
[spoiler title=”источники:”]
http://online-otvet.ru/matematika/5cea9d1696f4e19a2952a635
http://poschitat.online/radius-okruzhnosti
[/spoiler]