Радиус описанной окружности прямоугольника
Радиус описанной окружности прямоугольника равен половине его диагонали
a , b – стороны прямоугольника
d – диагональ
Формула радиуса описанной окружности прямоугольника (R):
Калькулятор – вычислить, найти радиус описанной окружности прямоугольника через стороны
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:

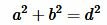 . . |
(1) |
Из равенства (1) найдем d:
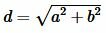 . . |
(2) |
Пример 1. Стороны прямоугольника равны  . Найти диагональ прямоугольника.
. Найти диагональ прямоугольника.
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя  в (2), получим:
в (2), получим:

Ответ: 
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac<large d> <large 2>) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac<large sqrt> <large 2>) | (4) |
Пример 2. Стороны прямоугольника равны  . Найти радиус окружности, описанной вокруг прямоугольника.
. Найти радиус окружности, описанной вокруг прямоугольника.
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя  в (4), получим:
в (4), получим:


Ответ: 
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
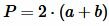 |
(5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны  . Найти периметр прямоугольника.
. Найти периметр прямоугольника.
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя  в (5), получим:
в (5), получим:

Ответ: 
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 |
(6) |
 |
(7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 |
(8) |
 |
(9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
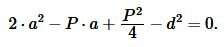 |
(10) |
Вычислим дискриминант квадратного уравнения (10):
Сторона прямоугольника вычисляется из следующих формул:
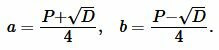 |
(12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
( frac< P><2>>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).
Пример 4. Диагональ прямоугольника равна  , а периметр равен
, а периметр равен  . Найти стороны прямоугольника.
. Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим  ,
,  в (11):
в (11):

Подставляя значения  и
и  в первую формулу (12), получим:
в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения  и
и  в формулу, получим:
в формулу, получим:

Ответ:  ,
, 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Радиус описанной окружности прямоугольника
Как известно, прямоугольником является четырехугольник с прямыми углами. Противоположные углы прямоугольника в сумме составляют 180°, соответственно, вокруг него можно описать одну окружность, при этом, вершины прямоугольника должны быть расположены на этой окружности. Центр прямоугольника и описанной вокруг него окружности размещен в месте пересечения диагоналей. Диагонали прямоугольника равны. Если известны стороны прямоугольника, можно рассчитать величину диагоналей по теореме Пифагора. Диагональ прямоугольника является в то же время и диаметром описанной окружности. R описанной окружности представляет половину диагонали прямоугольника и рассчитывается путем извлечения квадратного корня из суммы квадратов его сторон деленный на 2 или как половина его диагонали:

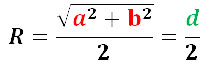
d — диагональ;
a, b — величины сторон прямоугольника.
Если известны стороны прямоугольника или диагонали, можно быстро найти R описанной окружности с помощью калькулятора.
[spoiler title=”источники:”]
http://matworld.ru/geometry/pryamougolnik.php
[/spoiler]
Радиус окружности прямоугольника с учетом площади и угла между диагональю и шириной
Идти
Окружность прямоугольника = 1/2*(sqrt(Площадь прямоугольника*cot((pi/2)-Угол между диагональю и шириной прямоугольника)))/(cos((pi/2)-Угол между диагональю и шириной прямоугольника))
Радиус окружности прямоугольника с учетом площади и тупого угла между диагоналями
Идти
Окружность прямоугольника = 1/2*(sqrt(Площадь прямоугольника*cot((pi–Тупой угол между диагоналями прямоугольника)/2)))/(cos((pi–Тупой угол между диагоналями прямоугольника)/2))
Радиус окружности прямоугольника с учетом площади и острого угла между диагоналями
Идти
Окружность прямоугольника = 1/2*(sqrt(Площадь прямоугольника*cot(Острый угол между диагоналями прямоугольника/2)))/(cos(Острый угол между диагоналями прямоугольника/2))
Радиус окружности прямоугольника с заданными площадью и углом между диагональю и длиной
Идти
Окружность прямоугольника = 1/2*(sqrt(Площадь прямоугольника*cot(Угол между диагональю и длиной прямоугольника)))/(cos(Угол между диагональю и длиной прямоугольника))
Радиус окружности прямоугольника по периметру и ширине
Идти
Окружность прямоугольника = sqrt(Периметр прямоугольника^2-(4*Периметр прямоугольника*Ширина прямоугольника)+(8*Ширина прямоугольника^2))/4
Радиус окружности прямоугольника по периметру и длине
Идти
Окружность прямоугольника = sqrt(Периметр прямоугольника^2-(4*Периметр прямоугольника*Длина прямоугольника)+(8*Длина прямоугольника^2))/4
Радиус окружности прямоугольника по периметру и углу между диагональю и шириной
Идти
Окружность прямоугольника = 1/2*(Периметр прямоугольника/2*1/(sqrt(1+sin(2*((pi/2)-Угол между диагональю и шириной прямоугольника)))))
Радиус окружности прямоугольника по периметру и тупому углу между диагоналями
Идти
Окружность прямоугольника = 1/2*(Периметр прямоугольника/2*1/(sqrt(1+sin(2*((pi–Тупой угол между диагоналями прямоугольника)/2)))))
Радиус окружности прямоугольника по периметру и острому углу между диагоналями
Идти
Окружность прямоугольника = 1/2*(Периметр прямоугольника/2*1/(sqrt(1+sin(2*(Острый угол между диагоналями прямоугольника/2)))))
Радиус окружности прямоугольника по периметру и углу между диагональю и длиной
Идти
Окружность прямоугольника = 1/2*(Периметр прямоугольника/2*1/(sqrt(1+sin(2*Угол между диагональю и длиной прямоугольника))))
Радиус окружности прямоугольника, заданный шириной и углом между диагональю и шириной
Идти
Окружность прямоугольника = 1/2*(Ширина прямоугольника*cosec((pi/2)-Угол между диагональю и шириной прямоугольника))
Радиус окружности прямоугольника по длине и углу между диагональю и шириной
Идти
Окружность прямоугольника = 1/2*(Длина прямоугольника*sec((pi/2)-Угол между диагональю и шириной прямоугольника))
Радиус окружности прямоугольника по ширине и тупому углу между диагоналями
Идти
Окружность прямоугольника = 1/2*(Ширина прямоугольника*cosec((pi–Тупой угол между диагоналями прямоугольника)/2))
Радиус окружности прямоугольника по площади и ширине
Идти
Окружность прямоугольника = 1/2*sqrt(Ширина прямоугольника^2+(Площадь прямоугольника/Ширина прямоугольника)^2)
Радиус окружности прямоугольника с заданной площадью и длиной
Идти
Окружность прямоугольника = 1/2*sqrt(Длина прямоугольника^2+(Площадь прямоугольника/Длина прямоугольника)^2)
Радиус окружности прямоугольника по ширине и острому углу между диагоналями
Идти
Окружность прямоугольника = 1/2*(Ширина прямоугольника*cosec(Острый угол между диагоналями прямоугольника/2))
Радиус окружности прямоугольника, заданный шириной и углом между диагональю и длиной
Идти
Окружность прямоугольника = 1/2*(Ширина прямоугольника*cosec(Угол между диагональю и длиной прямоугольника))
Радиус окружности прямоугольника с заданной длиной и углом между диагональю и длиной
Идти
Окружность прямоугольника = 1/2*(Длина прямоугольника*sec(Угол между диагональю и длиной прямоугольника))
Радиус окружности прямоугольника при заданной длине и остром угле между диагоналями
Идти
Окружность прямоугольника = Длина прямоугольника/(2*cos(Острый угол между диагоналями прямоугольника/2))
Радиус окружности прямоугольника при заданной длине и тупом угле между диагоналями
Идти
Окружность прямоугольника = Длина прямоугольника/(2*sin(Тупой угол между диагоналями прямоугольника/2))
Радиус окружности прямоугольника по площади и периметру
Идти
Окружность прямоугольника = 1/4*sqrt(Периметр прямоугольника^2-(8*Площадь прямоугольника))
Окружность прямоугольника
Идти
Окружность прямоугольника = sqrt(Длина прямоугольника^2+Ширина прямоугольника^2)/2
Радиус окружности прямоугольника при заданном диаметре окружности
Идти
Окружность прямоугольника = Диаметр окружности прямоугольника/2
Радиус окружности прямоугольника по диагонали
Идти
Окружность прямоугольника = Диагональ прямоугольника/2
Радиус окружности прямоугольника по периметру и ширине
Идти
Окружность прямоугольника = sqrt(Периметр прямоугольника^2-(4*Периметр прямоугольника*Ширина прямоугольника)+(8*Ширина прямоугольника^2))/4
Радиус окружности прямоугольника по периметру и длине
Идти
Окружность прямоугольника = sqrt(Периметр прямоугольника^2-(4*Периметр прямоугольника*Длина прямоугольника)+(8*Длина прямоугольника^2))/4
Диаметр окружности прямоугольника
Идти
Диаметр окружности прямоугольника = sqrt(Длина прямоугольника^2+Ширина прямоугольника^2)
Окружность прямоугольника
Идти
Окружность прямоугольника = sqrt(Длина прямоугольника^2+Ширина прямоугольника^2)/2
Радиус окружности прямоугольника при заданном диаметре окружности
Идти
Окружность прямоугольника = Диаметр окружности прямоугольника/2
Диаметр окружности прямоугольника по радиусу окружности
Идти
Диаметр окружности прямоугольника = 2*Окружность прямоугольника
Радиус окружности прямоугольника по диагонали
Идти
Окружность прямоугольника = Диагональ прямоугольника/2
Радиус описанной окружности прямоугольника
Вокруг прямоугольника становится возможным описать окружность, так как сумма противоположных углов в нем равна 180° , а это обязательно условие для окружностей, описанных вокруг многоугольников. Такая окружность касается всех вершин прямоугольника, а ее центр находится в точке пересечения диагоналей прямоугольника. Если провести радиусы к вершинам прямоугольника, то станет очевидным, что они представляют собой половины диагоналей, а диагонали прямоугольника можно найти из теоремы Пифагора в прямоугольном треугольнике, стороны которого – это стороны прямоугольника. 
Геометрические фигуры. Прямоугольник. Формулы.
Диагональ прямоугольника — это всякий отрезок, который соединяет 2-е вершины противолежащих углов прямоугольника.
Диагонали прямоугольника имеют одинаковую длину.
Диагонали прямоугольника делятся точкой пересечения пополам.
Длина диагонали прямоугольника можно вычислить по теореме Пифагора. И она равняется квадратному корню из суммы квадратов длины и ширины.
Формулы для вычисления длины диагонали прямоугольника:
1. Формула диагонали прямоугольника через 2 стороны прямоугольника (по теореме Пифагора):

2. Формула диагонали прямоугольника через площадь и сторону:

3. Формула диагонали прямоугольника через периметр и сторону:

4. Формула диагонали прямоугольника через радиус окружности (описанной):
5. Формула диагонали прямоугольника через диаметр окружности (описанной):
6. Формула диагонали прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:

7. Формула диагонали прямоугольника через косинус угла, который прилегает к диагонали, и длину стороны, которая прилегает к этому углу:

8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:

Признаки прямоугольника.
Параллелограмм — это прямоугольник, если выполняются условия:
— Если диагонали его имеют одинаковую длину.
— Если квадрат диагонали параллелограмма равняется сумме квадратов смежных сторон.
— Если углы параллелограмма имеют одинаковую величину.
Стороны прямоугольника.
Длинная сторона прямоугольника является длиной прямоугольника, а короткая — ширина прямоугольника.
Формулы для определения длин сторон прямоугольника:
1. Формула стороны прямоугольника (длина и ширина прямоугольника) через диагональ и еще одну сторону:

2. Формула стороны прямоугольника (длина и ширина прямоугольника) через площадь и еще одну сторону:

3. Формула стороны прямоугольника (длина и ширина прямоугольника) через периметр и еще одну сторону:

4. Формула стороны прямоугольника (длина и ширина прямоугольника) через диаметр и угол α:
5. Формула стороны прямоугольника (длина и ширина прямоугольника) через диаметр и угол β:

Окружность, описанная вокруг прямоугольника.
Окружность, описанная вокруг прямоугольника — это круг, который проходит сквозь 4-ре вершины прямоугольника, с центром на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника:
1. Формула радиуса окружности, которая описана около прямоугольника через 2-е стороны:

2. Формула радиуса окружности, которая описана около прямоугольника через периметр квадрата и сторону:

3. Формула радиуса окружности, которая описана около прямоугольника через площадь квадрата:

4. Формула радиуса окружности, которая описана около прямоугольника через диагональ квадрата:

5. Формула радиуса окружности, которая описана около прямоугольника через диаметр окружности (описанной):

6. Формула радиуса окружности, которая описана около прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:

7. Формула радиуса окружности, которая описана около прямоугольника через косинус угла, который прилегает к диагонали, и длину стороны у этого угла:

8. Формула радиуса окружности, которая описана около прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:

Угол между стороной и диагональю прямоугольника.
Формулы для определения угла между стороной и диагональю прямоугольника:
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:

2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:

Угол между диагоналями прямоугольника.
Формулы для определения угла меж диагоналей прямоугольника:
1. Формула определения угла меж диагоналей прямоугольника через угол между стороной и диагональю:
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Радиус описанной окружности прямоугольника
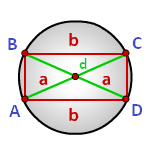
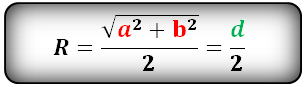
Формула радиуса описанной окружности прямоугольника (R):
Калькулятор — вычислить, найти радиус описанной окружности прямоугольника через стороны
Подробности Автор: Administrator Опубликовано: 09 сентября 2011 Обновлено: 13 августа 2021
Радиус описанной окружности прямоугольника
Радиус описанной окружности прямоугольника равен половине его диагонали

a, b – стороны прямоугольника
d – диагональ
Формула радиуса описанной окружности прямоугольника (R):

Калькулятор – вычислить, найти радиус описанной окружности прямоугольника через стороны
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 13 августа 2021
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
