Как найти радиус сектора окружности
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:

O — центр круга, OA — радиус круга.
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | ) 2 = π | D 2 | = π | D 2 | . |
| 2 | 2 2 | 4 |
Сектор круга. Площадь сектора
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:

Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.

Формула площади сектора:
| S = | πr 2 | · n = | πr 2 n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
можно представить в виде произведения
| πr 2 n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:

Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.

Площадь сегмента AMB будет вычисляться по формуле:
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
Как найти радиус окружности

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать – как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
 ,
,
где R – радиус круга, D – диаметр круга
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .






Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности



то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем



В случае, когда величина α выражена в в радианах, получаем
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
http://www.resolventa.ru/demo/diaggia6.htm
[/spoiler]
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
Информация по назначению калькулятора
Сектор круга – это часть окружности внутри круга, состоящая из дуги вместе с ее двумя радиусами. Часть окружности (также известная как дуга) и 2 радиуса окружности встречаются в обеих конечных точках дуги, образуя сектор. Форма сектора круга выглядит как кусочек пиццы или пирога. В геометрии круг – одна из самых совершенных фигур. Форма сектора окружности – самая простая форма в геометрии. У него есть свои собственные различные части. Например, диаметр, радиус, окружность, сегмент, сектор.
Круг разделен на два сектора, и разделенные части известны как второстепенные сектора и главные сектора.
Большая часть круга является основным сектором, в то время как меньшая часть является второстепенным сектором.
В случае полукругов окружность делится на два сектора одинакового размера.
2 радиуса встречаются в части окружности круга, известной как дуга, образуя сектор окружности.
Онлайн калькулятор предназначен для нахождения параметров сектора круга, таких как:
- Площадь сектора
- Длина дуги
- Радиус
- Периметр сектора
- Центральный угол сектора в градусах и радианах
– это объем пространства, занимаемого в пределах границы сектора круга. Сектор всегда начинается с центра круга. Полукруг также является сектором круга, в данном случае круг имеет два сектора одинакового размера.
Можно найти зная радиус и центральный угол в градусах (Ssek = ( α / 360° ) * πr2)
– находится путем умножения радиуса на центральный угол сектора в радианах (L = r * α)
– равен сумме длины дуги и двум радиусам (Psek = L + r + r)
Вы здесь
-
Радиус и угол сектора круга
Сектор круга является его частью, ограниченной двумя радиусами. Поскольку радиус является неизменным показателем для круга и его сектора, то сам сектор будет зависеть от длины дуги или центрального угла сектора, измеренного в градусах. Зная радиус и угол сектора круга, вычислить площадь сектора круга представляется возможным, разделив площадь самого круга на 360 градусов и умножив на данный угол.
S=πr^2 α/〖360〗^° =(r^2 α)/2Теперь через площадь сектора круга можно найти и длину дуги, разделив удвоенное значение на радиус. После подстановки приведенной для площади формулы сокращается радиус и число π, и остается произведение радиуса на угол сектора круга.
p=2S/r=2πr α/〖360〗^° =rα
Смотрите также
Окружность, круг, сегмент, сектор. Формулы и свойства
- Окружность – определение
- Круг – определение
- Радиус и диаметр окружности
- Основные свойства окружности
- Формулы длины окружности и площади круга
- Уравнение окружности
- Касательная окружности и ее свойства
- Секущая окружности и ее свойства
- Хорда окружности и ее свойства
- Центральный угол, вписанный угол и их свойства
- Дуга, длина дуги, градусная мера дуги
- Полуокружность и полукруг
- Сектор, площадь сектора
- Сегмент, площадь сегмента
- Концентрические окружности
- Кольцо
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равен единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
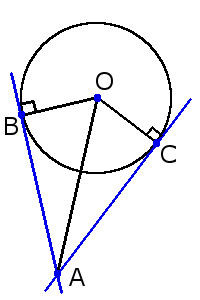
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
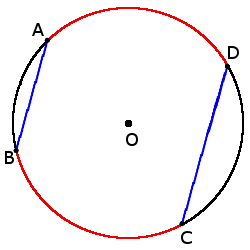
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
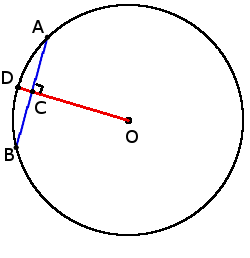
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
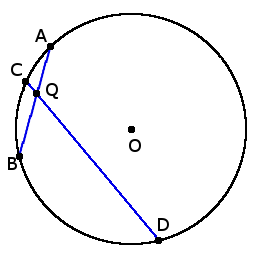
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
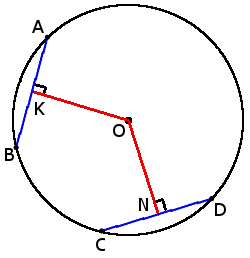
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK
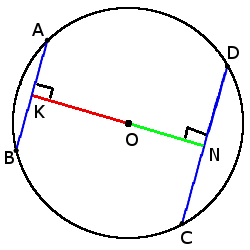
6. Чем больше хорда, тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
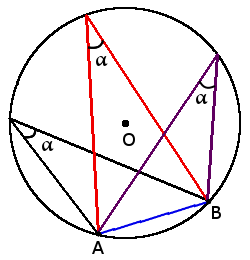
1. Все вписанные углы, которые опираются на одну дугу – равны.
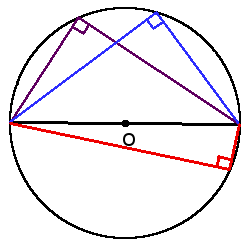
2. Вписанный угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
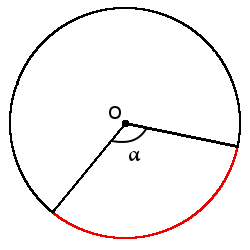
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
