Как определить радиус дуги или сегмента круга и найти центр
Иногда, при выполнении особо заковыристых работ по отделке приходится решать не совсем простые задачи. Например, имеется часть окружности, говоря по научному – дуга и для этой дуги нужно определить радиус и найти центр окружности.
Сделать это можно двумя методами. Первый метод основан на расчетах, а второй – прикладной. Сначала рассмотрим первый метод, его достоинства и недостатки, а затем второй.
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье “Расчет арочной перемычки”, поэтому здесь лишь приведу основные формулы:
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад – для того, чтобы напомнить формулы – есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше – то искомый центр дуги выше на прямой.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье “Записаться на прием к доктору”
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины – номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Категории:
- Расчет конструкций . Основы прикладной геометрии
Оценка пользователей:
8.5 (голосов: 2)
Переходов на сайт:
31889
Комментарии:
R = H/(1 – cos(a/2))
Радиус прямо пропорционален H.
Как так?
Я достаточно подробно ответил на ваш вопрос в статье “Расчет арочной перемычки”, где вы задали подобный вопрос.
Если угол не нужен для дальнейших расчетов, радиус находится проще – без тригонометрических функций и даже можно без калькулятора – на бумажке. R = L^2/(8*H) + H/2
Сначала термины:
Отрезок, соединяющий концы дуги называется хордой (a), а высота сегмента (перпендикуляр из середины хорды) — стрелкой (h).
Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. То есть R^2=(R-h)^2+(a/2)^2.
А что касается нахождения центра, то перпендикуляры к серединам хорд пересекаются в центре!
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье “Записаться на прием к доктору” (ссылка в шапке сайта).
Определение центра окружности и центра дуги окружности
Порядок определение центра
Взаимное пересечение перпендикуляров, восставленных в середине каждой хорды, определяет центр окружности (точку О). На фиг. 9,6 показано нахождение центра дуги окружности (построение аналогично предыдущему).
Выпрямление дуги окружности
Определение длины 1 дуги АВ окружности (приближенный способ, фиг. 10).
Через хорду АВ проводят перпендикуляр (фиг. 10,а), пересекающий дугу в точке К. Из точек С и D, как из центров, радиусами г, равными d— диаметру окружности, проводят две дуги до взаимного их пересечения в точке 01.
Расстояние между точками пересечения лучей 01А и O1B с касательной, проведенной к окружности в точке К, определяет приближенное значение спрямленной дуги (отрезок А1В1).
Расстояние между точками С1 и D1 определяет приближенную длину полуокружности. При отсутствии центра окружности
длина дуги АВ (фиг. 10,6) может быть определена следующим путем: хорду А В делят на четыре равные части; одну четвертую часть откладывают от точки В на дуге АВ; полученную точку С соединяют с точкой деления 1. Отрезок 1—С равен половине длины дуги АВ; CD — приближенное значение длины всей дуги АВ.
Определение длины окружности. Длину окружности определяют по формуле l=П*D, где l — длина окружности, П = 3,14159, a D—диаметр окружности. На фиг. 11,а показана длина l окружности диаметра D.
Графически длина окружности приближенно может быть определена путем суммирования длины двух сторон аз равностороннего треугольника и двух сторон а квадрата, вписанных в окружность, как это показано на фиг. 11,6 (2аз + 2а4). Точность определения — 0,01. На фиг. 11,в длина окружности определена следующим способом: из центра О под углом 30° проводят прямую до пересечения ее в точке А с касательной к окружности; от точки А откладывают отрезок АВ, равный трем радиусам R; из точки В, как из центра, радиусом ВМ проводят дугу окружности до пересечения с касательной прямой в точках С и D. Отрезок CD будет равен длине окружности. Точность определения — 0,0001.
Определение приближенной длины очерка эллипса (фиг. 12). Для определения длины очерка эллипса ACBD соединяют точки А и С и из центра О радиусом, равным АС, засекают на осях эллипса точки М и N. Измерив длину отрезка MN, умножают ее на 3,14 и получают приближенную длину очерка эллипса (l = 3,14*MN).
Определение центра окружности и центра дуги
Определение центра окружности (рис. 28).
- 1) Провести в окружности две непараллельные хорды АВ и CD.
- 2) К середине хорды А В восстановить перпендикуляр (см. деление отрезка на две равные части при помощи циркуля).
- 3) Выполнить аналогичное построение для хорды ВС.
Пересечение перпендикуляров является центром окружности.
Определение центра дуги окружности (рис. 29).
- 1) Назначить на дуге три произвольных точки А, В и С.
- 2) Соединить точки прямыми.
- 3) Через середины полученных хорд АВ и ВС провести перпендикуляры.
Точка О пересечения перпендикуляров является центром дуги.
Сопряжения
Сопряжением называется плавный переход от одной линии к другой.
Из всего многообразия сопряжений различных линий выделяют основные виды сопряжений:
- • сопряжение прямой линии с дугой окружности;
- • сопряжение двух различно расположенных прямых линий с помощью дуги окружности;
- • сопряжение дуг двух окружностей с помощью прямой линии;
- • сопряжение дуг двух окружностей с помощью третьей.
Дуги окружностей, с помощью которых выполняется сопряжение, называют дугами сопряжения. Для построения дуги сопряжения необходимо на чертеже выявить:
- • центр дуги сопряжения;
- • радиус этой дуги;
- • точки сопряжения, в которых дуга сопряжения переходит в сопрягаемые линии.
Задаваясь одним из этих параметров, остальные можно определить графически.
При сопряжении прямой линии с дугой окружности прямая линия является касательной к окружности. В этом случае центр дуги окружности О и точка сопряжения К лежат на перпендикуляре к сопрягаемой прямой (рис. 30).
При сопряжении дуг двух окружностей точка сопряжения К должна лежать на линии, соединяющей центры сопрягаемых дуг (рис. 31).
Сопряжение пересекающихся прямых линий с помощью дуги заданного радиуса.
Сопряжение двух взаимно перпендикулярных прямых а и b дугой окружности заданного радиуса R (рис. 32, а).
- 1) Из точки пересечения прямых как из центра провести дугу окружности радиусом R до пересечения с прямыми в точках А и В (рис. 32, б).
- 2) Из полученных точек/1 и В как из центров тем же радиусом провести дуги окружностей до взаимного пересечения в точке О (рис. 32, в).
3) Из точки О радиусом R провести дугу сопряжения (рис. 32, г). Точки А и В являются точками сопряжения.
Сопряжение двух пересекающихся прямых а и b под произвольным углом дугой заданного радиуса R (рис. 33, 34).
Центр сопряжения О должен лежать на расстоянии R от заданных прямых. Для его определения необходимо:
- 1) Из произвольных точек на заданных прямых провести дуги радиусом R.
- 2) Построить линии, касательные к дугам. Точка О пересечения этих линий является центром сопряжения (рис. 33, а).
- 3) Из точки О опустить перпендикуляры на заданные прямые.
Точки И и i? являются точками сопряжения (рис. 33,6).
4) Из точки О как из центра провести дугу радиуса R. Эта дуга является дугой сопряжения.
На рисунке 34 сопряжение прямых линий выполнено аналогично.
Сопряжение параллельных прямых дугой окружности. Если на одной из прямых а и b задана точка сопряжения А (рис. 35, а), сопряжение выполняют следующим образом.
- 1) Из точки А опустить перпендикуляр на прямую b (рис. 35, б).
- 2) Разделить отрезок АВ пополам (рис. 35, в).
- 3) Из точки О как из центра провести дугу сопряжения радиусом ОА (рис. 35, г).
Сопряжение дуги окружности радиуса R и прямой а дугой заданного радиуса Rj (рис. 36).
Для выполнения этого сопряжения сначала необходимо определить множество центров дуг радиуса Rx.
1) На расстоянии Rx от прямой а провести параллельную ей прямую т. Прямая т является множеством центров дуг радиуса Rx.
2) Из центра О провести дугу концентрической окружности радиусом (R + R). Точка Ох пересечения дуги с прямой т будет центром дуги сопряжения.
Точка сопряжения С получена на перпендикуляре, опущенном из точки 0 на прямую а, а точка В является точкой пересечения окружности с прямой, соединяющей точки О и Ох.
Сопряжение дуг двух окружностей с помощью прямой линии. Это сопряжение сводится к построению внешней (рис. 37) или внутренней (рис. 38) касательной к данным окружностям.
Построение внешней касательной, сопрягающей две окружности радиусов R и R (рис. 37, а).
- 1) Соединить центры окружностей.
- 2) Отрезок 00 разделить точкой О2 пополам.
- 3) Из точки О провести окружность радиусом (R — Rx), равным разности радиусов заданных окружностей (рис. 31,6).
- 4) На построенной окружности сделать засечки радиусом R2 = 020. Точки обозначены Е и D (рис. 37, в).
- 5) Продлить отрезки ОЕ и OD до пересечения с окружностью радиуса R. Полученные точки С и В являются точками сопряжения (рис. 37, г).
- 6) Соединить точки Ей D с центром Ох.
- 1) Из точек С и В параллельно отрезкам ОхЕ и OxD провести отрезки, сопрягающие две окружности.
Точки сопряжения на окружности радиуса R можно получить, опустив перпендикуляры из точки Ох к отрезкам ОхЕ и OxD.
Построение внутренних касательных, сопрягающих две окружности радиусов R и R (рис. 38, а).
- 1) Из середины отрезка ООх — точки 02 — проводят дугу радиусом R2 = 020 (рис. 38, б).
- 2) Из центра О проводят дугу радиусом (R + R), равным сумме радиусов заданных окружностей. В пересечении этих окружностей отмечают точки Е и D.
- 3) Точки Е п D соединить с точкой О (рис. 38, в). Точки С и В пересечения прямых ОЕ и OD с окружностью являются точками сопряжения.
- 4) Точки Е и D соединить с точкой О у.
- 5) Через точки С и В провести прямые линии параллельно отрезкам ЕО и DO у.
Прямые ССХ и ВВх являются касательными, сопрягающими заданные окружности. Точки сопряжения Су и В у лежат на пересечении перпендикуляров, проведенных из центра О, к прямым ССу и В By.
Построение сопряжения двух дуг окружностей. Сопряжение двух дуг окружностей может быть внешнее (рис. 39, а) и внутреннее (рис. 39, б). Точка сопряжения А лежит на прямой, соединяющей центры окружностей.
Расстояние между центрами при внешнем сопряжении равно сумме радиусов окружностей (R + Ry), а при внутреннем сопряжении — разности этих радиусов (R — Ry). В точке сопряжения А окружности имеют общую касательную t.
Построение сопряжения двух дуг окружностей дугой заданного радиуса.
Такой вид сопряжения может быть внешним, внутренним и смешанным.
Построение внешнего сопряжения двух дуг окружностей радиусов R и Ry с помощью дуги радиуса R2 (рис. 40, а). При внешнем сопряжении дуги находятся с внешней стороны дуги сопряжения, т.е. точки сопряжения представляют собой точки перегиба.
- 1) Из центра О радиусом (R + R2), а из центра Ох радиусом (Rx + R2) проводят дуги до пересечения в точке 02 (рис. 40, б). Точка 02 является центром дуги сопряжения.
- 2) Соединить точку 02 с центрами дуг О и Ох. Точки В и С, лежащие на линиях 020 и 020х, являются точками сопряжения (рис. 40, в).
- 3) Из точки 02 как из центра провести дугу сопряжения радиусом R2 (рис. 40, в).
Построение внутреннего сопряжения двух дуг окружностей радиусов R и Rx при помощи дуги радиуса R2 (рис. 41, а). При внутреннем сопряжении сопрягаемые дуги находятся внутри дуги сопряжения, т.е. дуга сопряжения и сопрягаемые дуги находятся по одну сторону касательных, проведенных через точки сопряжения. Точки сопряжения в этом случае представляют собой точки самоприкосновения.
Порядок построения следующий (рис. 41,5).
- 1) Из центра О провести дугу радиусом (Л2 – Л), а из центра Ох — дугу радиусом, равным (R2 — R<). В пересечении этих дуг получают точку 02 — центр дуги сопряжения.
- 2) Соединить точку 02 с центрами дуг О и О^. Точки В иВ, лежащие на прямых 020 и 020х, являются точками сопряжения.
- 3) Из точки 02 как из центра провести дугу сопряжения радиусом R2.
Построение смешанного сопряжения двух дуг окружностей радиусов Ru RC помощью дуги радиуса R2 (рис. 42, а). При смешанном сопряжении двух данных дуг окружностей третьей дугой одна сопрягаемая дуга находится внутри дуги сопряжения, а другая — вне ее, т.е. одна точка сопряжения является точкой самоприкосновения, а вторая — точкой перегиба.
Построение смешанного сопряжения аналогично построению внешнего и внутреннего сопряжений. При этом возможны два варианта.
1) Дуга сопряжения с дугой радиуса R имеет внутреннее сопряжение, а с дугой радиуса — внешнее (рис. 42, б).
При таком сопряжении из центра О необходимо провести дугу радиусом (R2 — R), а из центра Ох — радиусом (R2 + Ri). Пересечение проведенных дуг определяет центр дуги сопряжения — точку О2–
В этом случае точка В — точка самоприкосновения, а точка Вх — точка перегиба.
2) Дуга сопряжения с дугой радиуса R имеет внешнее сопряжение, а с дугой радиуса Ru внутреннее (рис. 42, в).
В этом случае из центра О необходимо провести дугу радиусом (/?2 + R), а из центра 0 — радиусом (R2 — R). Точка В стала точкой перегиба, а точка Вь точкой самоприкосновения.
На рисунке 43 показан случай смешанного сопряжения двух дуг окружностей третьей дугой заданного радиуса R2, когда расстояние а между центрами дуг меньше суммы их радиусов (R + R <).Построения ясны из чертежа.
[spoiler title=”источники:”]
http://www.cad-project.ru/opredelenie-czentra-okruzhnosti
http://bstudy.net/787728/tehnika/opredelenie_tsentra_okruzhnosti_tsentra_dugi
[/spoiler]
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
![]()
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
mistet409
Вопрос по геометрии:
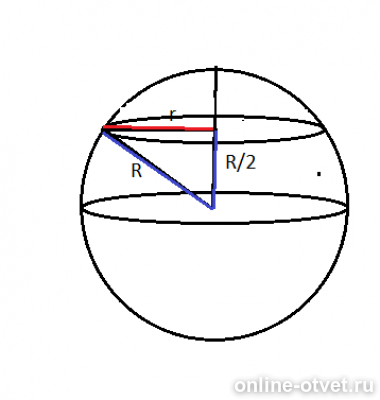
Через середину радиуса шара проведена перпендикулярная ему плоскость. Найдите радиус шара, если площадь сечения равна 243π
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
viteding748
Cм. рисунок
Радиус шара равен R
Радиус сечения r
S(сечения)=πr²
πr²=243π
r²=243
По теореме Пифагора ( на рисунке треугольник с синими и красной сторонами)
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
При всем таком длинном условии задачи, сводится она к нахождению длины гипотенузы в прямоугольном треугольнике , длина катетов которого нам известна.
По двум катетам найти гипотенузу. Проще не бывает задачек в геометрии.
Вся фишка в том, чтобы такую простую задачу вычленить в бытовом случае.
Это условие как раз и показывает школьникам, для чего нужна геометрия.

Обозначим конкретные точки вершин.
Тогда отрезок АВ по условию равен 72
Катет ВС будет половиной отрезка ВД – 42 : 2 = 21
Почему? да потому что отрезок АС по условию – радиус дуги. А радиус всерда исходит из центра окружности.
Осталось сделать вычисления, применив теорему Пифагора о том, что квадрат гипотенузы равен сумме квадратов катетов. В прямоугольном треугольнике.
Подставив значения длины отрезков и произведя вычисления получим


Ответ: радиус дуги арки кожуха равен 75 (единицам измерения)
