Download Article
Download Article
The radius of a sphere (abbreviated as the variable r or R) is the distance from the exact center of the sphere to a point on the outside edge of that sphere. As with circles, the radius of a sphere is often an essential piece of starting information for calculating the shape’s diameter, circumference, surface area, and/or volume. However, you can also work backward from the diameter, circumference, etc. to find the sphere’s radius. Use the formula that works with the information you have.
-

1
Find the radius if you know the diameter. The radius is half the diameter, so use the formula r = D/2. This is identical to the method used for calculating the radius of a circle from its diameter.[1]
- If you have a sphere with a diameter of 16 cm, find the radius by dividing 16/2 to get 8 cm. If the diameter is 42, then the radius is 21.
-

2
Find the radius if you know the circumference. Use the formula C/2π. Since the circumference is equal to πD, which is equal to 2πr, dividing the circumference by 2π will give the radius.[2]
- If you have a sphere with a circumference of 20 m, find the radius by dividing 20/2π = 3.183 m.
- Use the same formula to convert between the radius and circumference of a circle.
Advertisement
-

3
Calculate the radius if you know the volume of a sphere. Use the formula ((V/π)(3/4))1/3.[3]
The volume of a sphere is derived from the equation V = (4/3)πr3. Solving for the r variable in this equation gets ((V/π)(3/4))1/3 = r, meaning that the radius of a sphere is equal to the volume divided by π, times 3/4, all taken to the 1/3 power (or the cube root.)[4]
- If you have a sphere with a volume of 100 inches3, solve for the radius as follows:
- ((V/π)(3/4))1/3 = r
- ((100/π)(3/4))1/3 = r
- ((31.83)(3/4))1/3 = r
- (23.87)1/3 = r
- 2.88 in = r
- If you have a sphere with a volume of 100 inches3, solve for the radius as follows:
-

4
Find the radius from the surface area. Use the formula r = √(A/(4π)). The surface area of a sphere is derived from the equation A = 4πr2. Solving for the r variable yields √(A/(4π)) = r, meaning that the radius of a sphere is equal to the square root of the surface area divided by 4π. You can also take (A/(4π)) to the 1/2 power for the same result.[5]
- If you have a sphere with a surface area of 1,200 cm2, solve for the radius as follows:
- √(A/(4π)) = r
- √(1200/(4π)) = r
- √(300/(π)) = r
- √(95.49) = r
- 9.77 cm = r
- If you have a sphere with a surface area of 1,200 cm2, solve for the radius as follows:
Advertisement
-

1
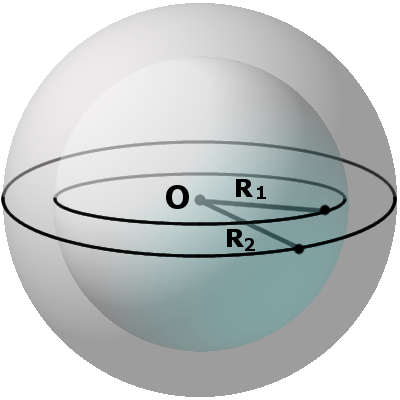
Identify the basic measurements of a sphere. The radius (r) is the distance from the exact center of the sphere to any point on the surface of the sphere. Generally speaking, you can find the radius of a sphere if you know the diameter, the circumference, the volume, or the surface area.
- Diameter (D): the distance across the sphere – double the radius. Diameter is the length of a line through the center of the sphere: from one point on the outside of the sphere to a corresponding point directly across from it. In other words, the greatest possible distance between two points on the sphere.
- Circumference (C): the one-dimensional distance around the sphere at its widest point. In other words, the perimeter of a spherical cross-section whose plane passes through the center of the sphere.
-
Volume (V): the three-dimensional space contained inside the sphere. It is the “space that the sphere takes up.”[6]
- Surface Area (A): the two-dimensional area on the outside surface of the sphere. The amount of flat space that covers the outside of the sphere.
- Pi (π): a constant that expresses the ratio of the circle’s circumference to the circle’s diameter. The first ten digits of Pi are always 3.141592653, although it is usually rounded to 3.14.
-

2
Use various measurements to find the radius. You can use the diameter, circumference, volume, and surface area to calculate the radius of a sphere. You can also calculate each of these numbers if you know the length of the radius itself. Thus, to find the radius, try reversing the formulas for these components’ calculations. Learn the formulas that use the radius to find diameter, circumference, volume, and surface area.[7]
- D = 2r. As with circles, the diameter of a sphere is twice the radius.
- C = πD or 2πr. As with circles, the circumference of a sphere is equal to π times the diameter. Since the diameter is twice the radius, we can also say that the circumference is twice the radius times π.
- V = (4/3)πr3. The volume of a sphere is the radius cubed (times itself twice), times π, times 4/3.
- A = 4πr2. The surface area of a sphere is the radius squared (times itself), times π, times 4. Since the area of a circle is πr2, it can also be said that the surface area of a sphere is four times the area of the circle formed by its circumference.
Advertisement
-

1
Find the (x,y,z) coordinates of the central point of the sphere. One way to think of the radius of a sphere is as the distance between the point at the center of the sphere and any point on the surface of the sphere. Because this is true, if you know the coordinates of the point at the center of the sphere and of any point on the surface, you can find the radius of the sphere simply by calculating the distance between the two points with a variant of the basic distance formula. To begin, find the coordinates of the sphere’s center point. Note that because spheres are three-dimensional, this will be an (x,y,z) point rather than an (x,y) point.
- This process is easier to understand by following along with an example. For our purposes, let’s say that we have a sphere centered around the (x,y,z) point (4, -1, 12). In the next few steps, we’ll use this point to help find the radius.
-

2
Find the coordinates of a point on the surface of the sphere. Next, you’ll need to find the (x,y,z) coordinates of a point on the surface of the sphere. This can be any point on the surface of the sphere. Because the points on the surface of a sphere are equidistant from the center point by definition, any point will work for determining the radius.
- For our example problem, let’s say that we know that the point (3, 3, 0) lies on the surface of the sphere. By calculating the distance between this point and the center point, we can find the radius.
-

3
Find the radius with the formula d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2).[8]
Now that you know the center of the sphere and a point on the surface, calculating the distance between the two will find the radius. Use the three-dimensional distance formula d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2), where d equals distance, (x1,y1,z1) equals the coordinates of the center point, and (x2,y2,z2) equals the coordinates of the point on the surface to find the distance between the two points.- In our example, we would plug in (4, -1, 12) for (x1,y1,z1) and (3, 3, 0) for (x2,y2,z2), solving as follows:
- d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2)
- d = √((3 – 4)2 + (3 – -1)2 + (0 – 12)2)
- d = √((-1)2 + (4)2 + (-12)2)
- d = √(1 + 16 + 144)
- d = √(161)
- d = 12.69. This is the radius of our sphere.
- In our example, we would plug in (4, -1, 12) for (x1,y1,z1) and (3, 3, 0) for (x2,y2,z2), solving as follows:
-

4
Know that, in general cases, r = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2).[9]
In a sphere, every point on the surface of the sphere is the same distance from the center point. If we take the three-dimensional distance formula above and replace the “d” variable with the “r” variable for radius, we get a form of the equation that can can find the radius given any center point (x1,y1,z1) and any corresponding surface point (x2,y2,z2).- By squaring both sides of this equation, we get r2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2. Note that this is essentially equal to the basic sphere equation r2 = x2 + y2 + z2 which assumes a center point of (0,0,0).
Advertisement
Add New Question
-
Question
How do I find the radius of a sphere if I know its volume is three times its surface area?

Write an equation whereby the volume [(4πr³) / 3] is set equal to three times the surface area (4πr²). Thus, [(4πr³) / 3] = 12πr². Divide both sides by 4π, so that r³/3 = r². Multiply by 3: r³ = 3r². Divide by r²: r = 3. In other words, a sphere’s volume can be three times its surface area only if its radius is 3 units.
-
Question
How do I calculate the radius of a sphere in my hand by using a ruler?

You can get a very close approximation by carefully measuring the circumference and dividing by twice-pi (6.28).
-
Question
Two solid spheres A & B are made of the same material. The radius of B is 3 times the radius of A, and the surface area of A is 20 cubic cm. How do I calculate the surface area of B?

The surface area (S) of a sphere equals 4πr², where r is the radius. Using that equation to solve for r: r = √(S / 4π). Now substitute 20 for S, and solve for the radius of sphere A: r = √(20 / 4π) = √(20 / 12.56) = √ 1.59 = 1.26 cm. That’s the radius of sphere A. The radius of sphere B is three times the radius of sphere A: (3)(1.26) = 3.79 cm. So for sphere B, the surface area is 4πr² = (4)(3.14)(3.79)² = 180.4 square centimeters. (That answer makes sense, because when you multiply the radius of a sphere by 3, you multiply its surface area by 3² or 9.) (We didn’t exactly triple the original surface area, because we rounded off some numbers along the way.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
This article was published on demand. However, if you are trying to get to grips with solid geometry for the first time, it’s arguably better to start the other end: calculating the properties of the sphere from the radius.
-
The order in which the operations are performed matters. If you are uncertain how priorities work, and your calculating device supports parentheses, then make sure to use them.
-
π or pi is a Greek letter that represents the ratio of the diameter of a circle to its circumference. It’s an irrational number and cannot be written as a ratio of 2 integers. Many approximations exist, 333/106 gives pi to four decimal places. Today most people memorize the approximation 3.14 which is usually sufficiently accurate for everyday purposes.
Show More Tips
Thanks for submitting a tip for review!
Advertisement
About This Article
Article SummaryX
If you know the diameter, you can find the radius of a sphere by dividing the diameter in half. If you know the circumference, you can find the radius by dividing the circumference by 2 times pi. To learn how to calculate the radius of a sphere using two points on the sphere, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 522,007 times.
Did this article help you?
Как найти радиус, если известен только диаметр
Если вы работаете с окружностью, вы часто пользуетесь терминами радиус и диаметр. Существует ряд простых формул, позволяющих найти радиус, зная длину окружности, площадь окружности и объем сферы. Есть ли формула, позволяющая узнать радиус, зная значение диаметра?

Инструкция
Диаметр (от древнегреческого διάμετρος «диаметр, поперечник») – это отрезок, который соединяет две точки на окружности или сфере, проходящий через центр этой окружности или сферы. Диаметром также называется длина этого отрезка. Радиус (от латинского radius «луч, спица колеса») – это отрезок, который соединяет центр окружности или сферы с любой точкой, находящейся на этой окружности или сфере, радиусом называется также длина этого отрезка.
Радиус принято обозначать буквой r, диаметр – буквой d. По определению радиус равен половине диаметра, а диаметр равен по величине двум радиусам. Соответственно d=2r, r=d/2. Значит, для того, чтобы узнать величину радиуса, зная диаметр, надо разделить диаметр на два.
Пример. Диаметр окружности d равен 8. Чему равен радиус r? Решение: r=d/2, значит, чтобы найти радиус, надо значение диаметра 8 разделить на два. 8/2=4. Ответ: r=4, радиус равен четырем.
Если вы ищите длину радиуса или диаметра, помните, что длина не может быть отрицательным числом. Поэтому если в ходе решения вы пришли к формуле d=2r= √x (квадратный корень из x), а x равен, к примеру 16, то диаметр d=±4,и радиус r=±2. Так как длина не может быть отрицательным числом, получаете ответ: диаметр равен четырем, радиус равен двум.
Интересен факт того, что в анатомии также встречается слово «радиус», оно обозначает одну из костей предплечья, лучевую кость (находится кнаружи и слегка кпереди от локтевой кости). А еще у слова радиус есть значение, уходящее истоками в древний Рим – это название короткого римского меча, который использовали легионеры для обороны. Легионер говорил: «Здесь я и Рим!» – чертил на земле этим мечом полосу и защищался до последнего.
Видео по теме
Источники:
- радиус на сайте формула.ру
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
#1
Очень часто людям требуется узнать точный размер какого-то объекта. На производстве, строительстве, моделировании и многом-многом другом точность является одним из главных правил. В природе очень распространены идеальные фигуры. Одним из таких тел является сфера. В стереометрии понятию «шар» даётся следующее определение: сфера – геометрическое место точек, равноудалённых от одной единственной – центра сферы. Расстояние, на котором находятся все эти точки, является постоянным и называется радиусом. Радиус является основным параметром и очень важно уметь вычислять его значение. Для проведения этой операции существует множество способов, как практических, так и теоретических. В большинстве из них фигурирует понятие числа «Пи», в котором обязательно нужно разобраться. Число «Пи» является постоянным иррациональным трансцендентным числом. Это значит, что его десятичная запись является бесконечной. Сама константа определяется отношением длины окружности к её радиусу. С древности учёные вычисляли значение этого числа, на данный момент известно уже более миллиарда знаков после запятой. На практике и, в частности, в данной статье понадобится не слишком точное значение данной константы. И хоть первые десять знаков выглядят как 3.3, чтобы найти радиус сферы будет использоваться округлённое значение 3,4.
#2
Первый способ годится, если имеется реальное сферическое тело, например, мяч для игры в настольный теннис. Как вычислить его радиус? Для этого достаточно использовать штангенциркуль, а именно поместить в раствор циркуля шарик, таким образом будет получено значение его диаметра. Оно равно сорока миллиметрам, если берётся стандартная модель. Теперь остаётся лишь поделить диаметр пополам и получится точное значение радиуса, а именно 20 мм. Для подобных случаев формула будет иметь вид R = D/2, (где R – радиус, а D – диаметр сферы) . Однако, часто приходится работать с абстрактными телами и вычислить их диаметр на практике невозможно. В таком случае, для нахождения радиуса необходимо знать значение какой-либо другой величины, например объёма или площади поверхности. Важно рассмотреть каждый из таких примеров отдельно, так как решение будет отличаться существенно. Будет предоставлен лёгкий способ найти радиус сферы, формула прилагается сама собой.
#3
Пусть дана сфера, площадь поверхности (S) которой равна 10 сантиметров квадратных. Найти её радиус. Для начала следует вспомнить общую формулу для вычисления площади поверхности шара, а именно: S = 4*Pi*(R^2) . Теперь нужно пошагово избавить значение Rот посторонних множителей и степени: R^2 = S / (4*Pi) , отсюда Rбудет равно корню квадратному из S / 4*Pi. Теперь имеется всё необходимое для решения исходной задачи, следует подставить известную Sв формулу: R = 10 / (4*Pi) . Далее потребуется помощь калькулятора: Pi*4 = 4 * 3,4 = 2,6. Далее выполняется операция деления: 10 / 2,6 = 0,3. Корень квадратной из данной величины равен 0.2, округлив данное значение до десятых, получится 0,9. Также не стоит забывать и о соблюдениях размерности, площадь была дана в сантиметрах квадратных, значит ответ будет в обычных сантиметрах. Ответ: сфера имеет радиус 0,9 см. Для всех подобных задач общая формула будет выглядеть так: R = √(S/(4*Pi) ) , где R – радиус, а S – площадь поверхности.
#4
Следующий пример. Дан шар объёмом 48 литров. Вычислить его радиус. Для решения данной задачи следует прибегнуть к формуле объёма шара. V = 4/3 * Pi * R^3. Как и в прошлом примере, следует выразить радиус в чистом виде: R^3 = (V * 3/4) / Pi. После извлечения корня кубического получится R = sqrt[3]((V * 3/4) / Pi) . Обозначение “sqrt[3]” означает кубический корень. Теперь стоит подставить объём в формулу и произвести вычисления: R = sqrt[3]((48 * 3/4) / Pi) = sqrt[3](36 / Pi) = sqrt[3](1,8) = 2,4. Важное внимание следует уделить размерности в этом случае, ведь объём дан в литрах, а ответ требуется дать в величинах, измеряющих длину.
#5
Стоит отметить, что 1 литр равен одному дециметру кубическому, следовательно ответ получен в дециметрах. Ответ: 2,5 дециметров или 2,5 сантиметра. Для всех подобных задач радиус можно вычислить с помощью формулы R = sqrt[3]((V * 3/4) / Pi) , где R – радиус, sqrt[3] – корень кубический, а V – объём шара. На практике, не имея возможность вычислить диаметр, но имея возможность найти объём шара, радиус сферы можно рассчитать с помощью воды и мензурки. Для этого нужно налить 100 мл воды в мензурку, полностью опустить в неё шар, зафиксировать новое значение. Из него вычесть 100 мл – это и будет объём шара. Далее производить действия по аналогии с последней задачей.
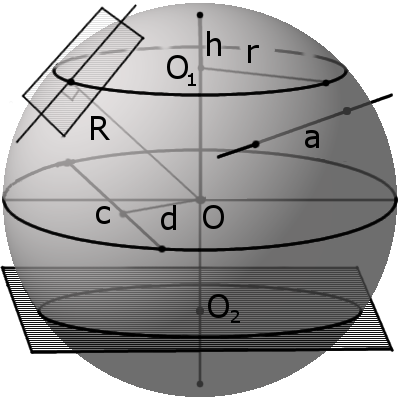
Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Формула. Объём шара:
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2
Основные свойства сферы и шара
Секущая, хорда, секущая плоскость сферы и их свойства
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.
Касательная, касательная плоскость к сфере и их свойства
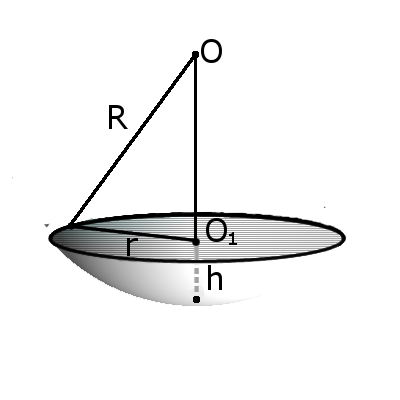
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

S = π R(2 h + √ 2 h R – h 2 )
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение радиуса шара: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус шара и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса шара

1. Через объем
Радиус шара вычисляется по формуле:

V – объем шара; равен трем четвертым произведения его радиуса в кубе и числа π .

π – число, приближенное значение которого равняется 3,14.
2. Через площадь поверхности
Радиус шара рассчитывается таким образом:

S – площадь поверхности шара; равна четырем его радиусам в квадрате, умноженным на число π .
S = 4 π R 2
Примеры задач
Задание 1
Объем шара составляет 904,32 см 3 . Найдите его радиус.
Решение:
Воспользовавшись первой формулой получаем:
Задание 2
Вычислите радиус шара, если площадь его поверхности равна 314 см 2 .
Решение:
В данном случае рассчитать радиус шара можно, применив 2-ю формулу (через площадь поверхности):
Площадь поверхности шара формула и калькулятор онлайн
Что такое шар?
В стереометрии есть большой раздел, который называется фигуры вращения. Об этом редко говорят в школе, но плоские фигуры можно вращать вокруг какой-либо оси или точки. Так получаются объемные фигуры.
Стереометрия это наука о фигурах в пространстве. Простейшими единицами стереометрии является точка, прямая и плоскость.
Например, цилиндр образован вращением прямоугольника или квадрата. Поэтому, если рассечь цилиндр плоскостью, то сечение примет форму того самого квадрата или прямоугольника, который вращали, чтобы получить фигуру.
Так же и шар образован вращением. Как не трудно догадаться, основной для шара послужил круг. Причем сразу стоит сказать, что именно круг, а не окружность.
Следует понимать, что круг и окружность разные фигуры. Так окружность представляет собой набор точек равноудаленных от центра. Переводя на более простой язык окружность – это сама линия и центр окружности. А круг включает в себя и все внутреннее пространство. У окружности не может быть площади.
То есть, шар имеет какое-то внутренне заполненное пространство. Интересно, что сфера так же имеет пространство внутри, только условно полое.
Формулы для вычисления радиуса

- Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см. Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).

- Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см.
- Такая же формула используется при вычислении радиуса и длины окружности круга.

- Например, дан шар с объемом 100 см 3 . Радиус этого шара вычисляется так:
- ((V/π)(3/4)) 1/3 = r
- ((100/π)(3/4)) 1/3 = r
- ((31,83)(3/4)) 1/3 = r
- (23,87) 1/3 = r
- 2,88 см = r

- Например, дан шар с площадью поверхности 1200 см 3 . Радиус этого шара вычисляется так:
- √(A/(4π)) = r
- √(1200/(4π)) = r
- √(300/(π)) = r
- √(95,49) = r
- 9,77 см = r
V = 4/3 πr3,
где V — объем, r — радиус шара.
Отсюда, радиус шара равен корню кубическому из объема шара деленного на три четвертых Пи:
Определение радиуса сферы при помощи площади ее поверхности
Допустим, нам дана сфера вместе с площадью её поверхности. В таком случае мы будем использовать формулу площади её поверхности для того, чтобы вычислить радиус.

где S – это площадь поверхности сферы, число Пи = 3,14.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.

Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:

- S = 4 * 3,14 * 10²;
- S мяча равна ≈ 1256 см².
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).


Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).



Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).



Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс , у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .



По той же причине всю сферу можно рассматривать как сферический пояс , у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).



Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).


Высотой шарового сектора называют высоту его сферического сегмента .
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы .
Объем шара через длину окружности

Формула для нахождения объема шара через длину окружности: <6pi^3>> , где L — длина окружности шара.
Эта формула легко выводится формулы объема шара через его радиус и формулы для нахождения длины окружности
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2

3. Параметрическое уравнение сферы с центром в точке ( x 0, y 0, z 0):
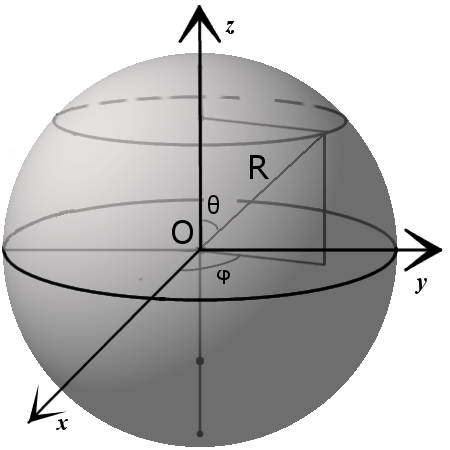
x = x 0 + R · sin θ · cos φ y = y 0 + R · sin θ · sin φ z = z 0 + R · cos θ
где θ ϵ [0, π ], φ ϵ [0,2 π ].
Определение радиуса сферы при помощи объема шара
Если нам дан объём шара, ограниченного сферой, то радиус находится так:

где V – это объём шара, число Пи = 3,14.
Определение основных величин

- Диаметр (D) – это отрезок, который соединяет две точки на поверхности шара и проходит через его центр (то есть это наибольшее расстояние между противоположными точками, лежащими на поверхности шара). Диаметр равен удвоенному радиусу.
- Длина окружности (С) представляет собой длину окружности большого круга, то есть круга, который образует секущая плоскость, проходящая через центр шара.
- Объем (V) – это значение трехмерного пространства, занимаемого шаром. [6]
- Площадь поверхности (А) – это значение двумерного (плоского) пространства, ограниченного поверхностью шара.
- Пи (π) – это постоянная, которая равна отношению длины окружности к ее диаметру. Первыми десятью цифрами этой постоянной являются 3,141592653, но зачастую число Пи округляется до 3,14.

- D = 2г. Как и в случае круга , диаметр шара в два раза больше его радиуса.
- C = πD = 2πr. Как и в случае круга , длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара.
- V = (4/3)πr 3 . Объем шара равен произведению 4/3 на π и на радиус в кубе. [7]
- А = 4πr 2 . Площадь поверхности шара равна учетверенному произведению π на радиус в квадрате. Так как площадь круга равна πr 2 , то площадь поверхности шара в четыре раза больше площади круга, который образует секущая плоскость, проходящая через центр шара.
r = С / 2π
π — величина постоянная, равна отношению длины окружности к диаметру. Число Пи, равное 3,141592653… обычно округляется до 3,14.
— по площади шара.
Площадь шара равна произведению четырех пи на квадрат радиуса:
Нахождение радиуса по расстоянию между двумя точками

- Рассмотрим пример. Дан шар с центром с координатами (4,-1,12). Воспользуйтесь этими координатами, чтобы найти радиус шара.

- В нашем примере допустим, что некоторая точка, лежащая на поверхности шара, имеет координаты (3,3,0). Вычислив расстояние между этой точкой и центром шара, вы найдете радиус.

- В рассматриваемом примере вместо (x1,y1,z1) подставьте (4,-1,12), а вместо (x2,y2,z2) подставьте (3,3,0):
- d = √((x2 – x1) 2 + (y2 – y1) 2 + (z2 – z1) 2 )
- d = √((3 – 4) 2 + (3 – -1) 2 + (0 – 12) 2 )
- d = √((-1) 2 + (4) 2 + (-12) 2 )
- d = √(1 + 16 + 144)
- d = √(161)
- d = 12,69. Это искомый радиус шара.

- Возведите обе стороны этого уравнения в квадрат, и получите r 2 = (x2 – x1) 2 + (y2 – y1) 2 + (z2 – z1) 2 . Отметьте, что это уравнение соответствует уравнению сферы r 2 = x 2 + y 2 + z 2 с центром с координатами (0,0,0).
C = πD = 2πr
Отсюда, радиус равен частному от деления длины окружности © на 2 пи:
Через площадь поверхности
Радиус шара рассчитывается таким образом:

S – площадь поверхности шара; равна четырем его радиусам в квадрате, умноженным на число π .
S = 4 π R 2
Одиннадцать свойств
В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:


- Точки на сфере находятся на одинаковом расстоянии от одной фиксированной, называемой центром. Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
- Контуры и плоские участки сферы являются кругами. Это однозначное свойство, которое определяет шар.
- Сфера имеет постоянную ширину и обхват. Ширина поверхности — это расстояние между парами параллельных касательных плоскостей. Множество других замкнутых выпуклых поверхностей имеют постоянную ширину, например, тело Мейснера. Обхват поверхности — это окружность границы её ортогональной проекции на плоскость. Каждое из этих свойств подразумевает другое.
- Все точки сферы омбилические. В любой точке поверхности вектор нормали расположен под прямым углом к ней, поскольку шар — это линии, выходящие из его центра. Пересечение плоскости, которая содержит нормаль с поверхностью, сформирует кривую — нормальное сечение. Любая замкнутая поверхность будет иметь как минимум четыре точки, называемых омбилическими. Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
- У шара нет центра поверхности. Например, два центра, соответствующие минимальной и максимальной секционной кривизне, называются фокальными точками, а совокупность всех таких точек образует одноимённую поверхность. И только у шара она преобразуется в единую точку.
- Все геодезические сферы являются замкнутыми кривыми. Для этой фигуры они большие круги. Многие другие поверхности разделяют это свойство.
- Имеет наименьшую площадь при наибольшем объёме. Это определяет шар однозначно. Например, мыльный пузырь: его окружает фиксированный объём, поверхностное натяжение минимизирует площадь его поверхности для такого объёма. Конечно, пузырь не будет идеальным шаром, поскольку внешние силы, такие как гравитация, будут искажать его форму.
- Сфера — единственная вложенная поверхность, у которой нет границы или сингулярностей с постоянной положительной средней кривизной.
- Сфера имеет наименьшую общую среднюю кривизну среди всех выпуклых тел с заданной площадью поверхности.
- Шар имеет постоянную гауссову кривизну. Это внутреннее свойство, которое определяется путём измерения длины и углов и не зависит от того, как поверхность встроена в пространство.
Сфера превращается в себя трёхпараметрическим семейством жёстких движений. Любое вращение вокруг линии, проходящей через начало координат, может быть выражено как комбинация вращений вокруг трёхкоординатной оси.
[spoiler title=”источники:”]
http://exceltut.ru/ploshhad-poverhnosti-shara-formula-i-kalkulyator-onlajn/
[/spoiler]
Радиус шара
Радиус
Отрезок, соединяющий центр шара с любой точкой на его поверхности, является радиусом шара, обозначается как r или R. В зависимости от исходных данных радиус шара можно вычислить:
— по диаметру. Как известно, радиус шара равен половине его диаметра:
г = D/2,
где г — радиус, D — диаметр шара.
— по длине окружности.
Длина окружности © равна произведению пи на диаметр (D), через радиус шара — удвоенному произведению пи на радиус ®:
C = πD = 2πr
Отсюда, радиус равен частному от деления длины окружности © на 2 пи:
r = С / 2π
π — величина постоянная, равна отношению длины окружности к диаметру. Число Пи, равное 3,141592653… обычно округляется до 3,14.
— по площади шара.
Площадь шара равна произведению четырех пи на квадрат радиуса:
S=4πr2,
где S — площадь шара, r — радиус.
Из этой формулы выводим форму радиуса:
r = √S / 4π,
т.е. радиус равен корню квадратному из площади шара деленной на четыре пи.
— по объему шара.
Объем шара равен произведению четырех третьих на число пи и на радиус шара в кубе:
V = 4/3 πr3,
где V — объем, r — радиус шара.
Отсюда, радиус шара равен корню кубическому из объема шара деленного на три четвертых Пи:
