Как найти радиус сферы описанной около призмы

Призма, вписанная в сферу

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу

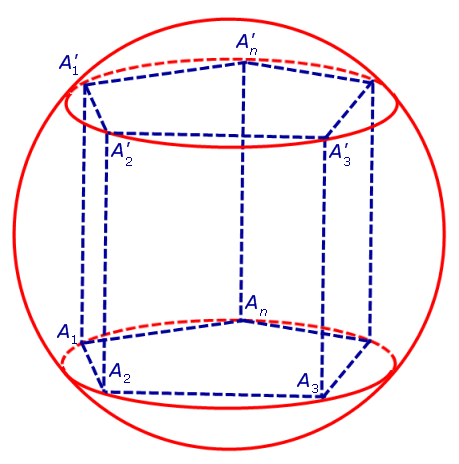
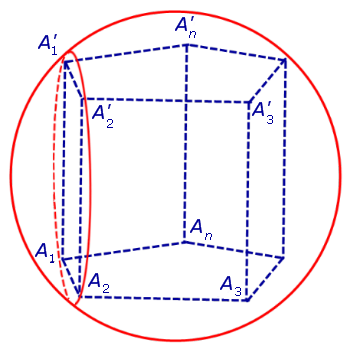
Определение 1. Призмой, вписанной в сферу, называют такую призму, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если призма вписана в сферу, то сферу называют описанной около призмы.

Теорема. Около призмы можно описать сферу тогда и только тогда, когда выполнены следующие два условия:

1. Призма является прямой призмой;
2. Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если n – угольная призма A₁A₂ . A_nA’₁A’₂ . A’_n вписана в сферу, то оба условия теоремы выполнены.

Для этого заметим, что плоскость каждого из оснований призмы пересекает сферу по окружности, на которой лежат вершины этого основания. Таким образом, многоугольники, являющиеся основаниями призмы, оказываются вписанными в окружности (рис. 1), то есть второе условие теоремы выполнено.

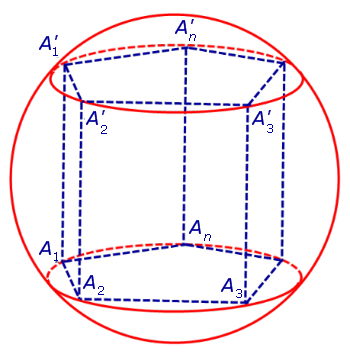
Каждая из боковых граней призмы также вписана в окружность (рис. 2).

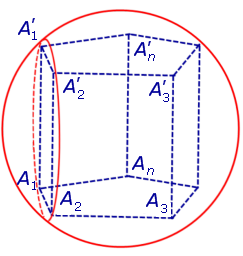
Рассмотрим какое-нибудь боковое ребро призмы, например, A₂A’₂. Поскольку это ребро перпендикулярно к ребрам основания A₁A₂ и A₂A₃ , то в силу признака перпендикулярности прямой и плоскости заключаем, что боковое ребро A₂A’₂ перпендикулярно к плоскости основания призмы, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма вписана в сферу, то оба условия теоремы выполнены.

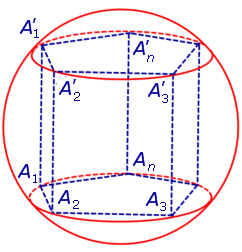
Для этого обозначим символом O₁ центр окружности радиуса r , описанной около нижнего основания призмы, а символом O’₁ обозначим центр окружности, описанной около верхнего основания призмы (рис. 3).

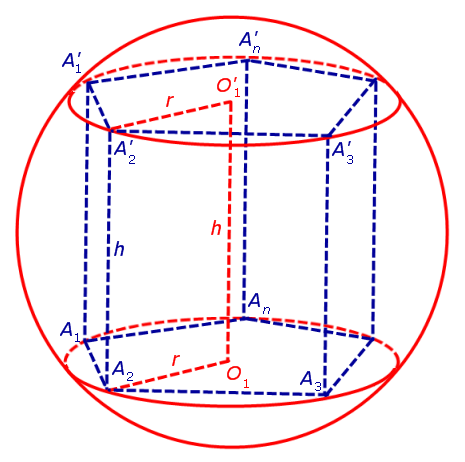
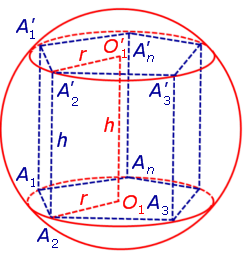
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны.

Согласно утверждению 1 из раздела «Призмы, вписанные в цилиндры» отрезок O₁O’₁, соединяющий центры окружностей, описанных около нижнего и верхнего оснований призмы, параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок O₁O’₁ перпендикулярен плоскости основания призмы и равен h.

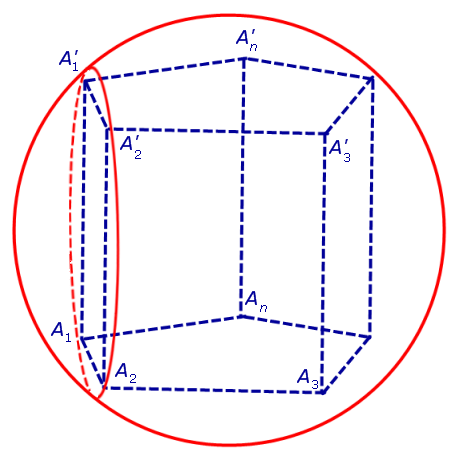
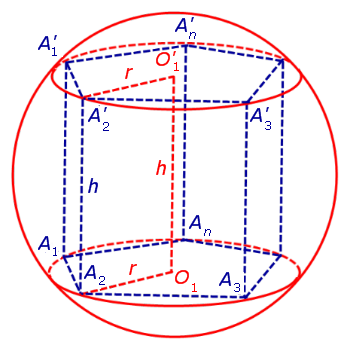
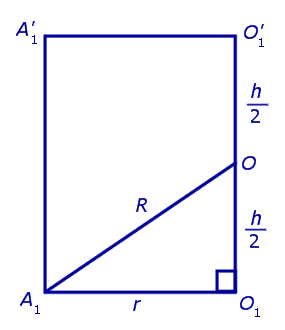
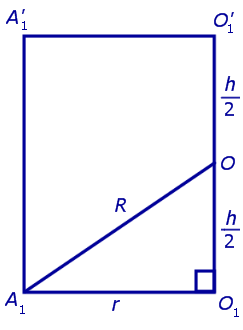
Обозначим буквой O середину отрезка O₁O’₁ и докажем, что все вершины призмы будут находиться на одном и том же расстояниии от точки O (рис. 4).

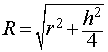(1)

от всех вершин призмы. Отсюда следует, что точка O является центром сферы радиуса R , описанной около призмы.

Следствие 1. Около любой прямой треугольной призмы можно вписать сферу.

Следствие 2. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать сферу.

Следствие 3. Около любой правильной призмы можно описать сферу.

Для доказательства следствия 3 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.

Радиус сферы, описанной около правильной n – угольной призмы

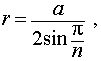
то из формулы (1) получаем выражение для радиуса описанной сферы

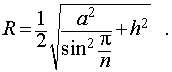(2)

Ответ.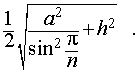

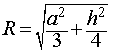
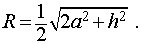
Следствие 6. Радиус сферы, описанной около около правильной шестиугольной призмы с высотой h и ребром основания a равен

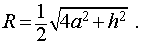
Отношение объема правильной n – угольной призмы к объему шара, ограниченного описанной около призмы сферой

Задача 2. Около правильной n – угольной призмы с высотой h и ребром основания a описана сфера. Найти отношение объемов призмы и шара, ограниченного сферой, описанной около данной призмы.

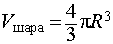
Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около призмы сферой, через высоту и ребро основания призмы:

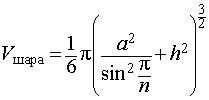
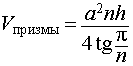
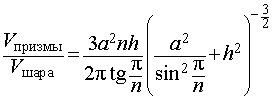
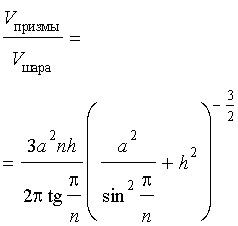
Ответ.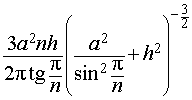

Следствие 7. Отношение объема правильной треугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

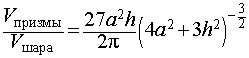
Следствие 8. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

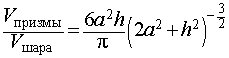
Следствие 9. Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Радиус описанной сферы и ребро “A” треугольной призмы

Свойства

Зная радиус сферы, описанной вокруг правильной треугольной призмы с равносторонним треугольником в основании, можно найти сторону этого основания и затем посчитать высоту основания, радиусы вписанной и описанной окружностей около него, а также площадь. a=√(6/5) R_1 h=a/√2=√(3/5) R_1 r=a/(2√3)=2√(2/5) R_1 R=a/√3=√(2/5) R_1 S=(√3 a^2)/4=(3√3 〖R_1〗^2)/10

Боковое ребро треугольной призмы в совокупности с радиусом описанной сферы позволяет вычислить диагональ боковой стороны, периметр призмы и площадь боковой, а затем и полной поверхности призмы. d=√(a^2+b^2 )=√(6/5 〖R_1〗^2+b^2 ) P=3(2a+b)=3(2√(6/5) R_1+b) S_(б.п.)=3ab=3b√(6/5) R_1 S_(п.п.)=3b√(6/5) R_1+(3√3 〖R_1〗^2)/5

Чтобы найти объем треугольной призмы через радиус описанной сферы и боковое ребро, нужно подставить в формулу объема необходимое выражение вместо площади основания и умножить его на боковое ребро. V=S_(осн.) b=(3√3 〖R_1〗^2)/10 b

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/radius-okruzhnosti

http://geleot.ru/education/math/geometry/calc/prism/radius_sphere_and_edge_a

[/spoiler]

Зная радиус сферы, описанной вокруг правильной треугольной призмы с равносторонним треугольником в основании, можно найти сторону этого основания и затем посчитать высоту основания, радиусы вписанной и описанной окружностей около него, а также площадь.
a=√(6/5) R_1
h=a/√2=√(3/5) R_1
r=a/(2√3)=2√(2/5) R_1
R=a/√3=√(2/5) R_1
S=(√3 a^2)/4=(3√3 〖R_1〗^2)/10

Боковое ребро треугольной призмы в совокупности с радиусом описанной сферы позволяет вычислить диагональ боковой стороны, периметр призмы и площадь боковой, а затем и полной поверхности призмы.
d=√(a^2+b^2 )=√(6/5 〖R_1〗^2+b^2 )
P=3(2a+b)=3(2√(6/5) R_1+b)
S_(б.п.)=3ab=3b√(6/5) R_1
S_(п.п.)=3b√(6/5) R_1+(3√3 〖R_1〗^2)/5

Чтобы найти объем треугольной призмы через радиус описанной сферы и боковое ребро, нужно подставить в формулу объема необходимое выражение вместо площади основания и умножить его на боковое ребро.
V=S_(осн.) b=(3√3 〖R_1〗^2)/10 b

3.4. Вписанные и описанные многогранники

Среди множества выпуклых многогранников выделим два важных семейства: вписанные и описанные многогранники.

Определение 22

Выпуклый многогранник называют вписанным, если все его вершины лежат на сфере. Эта сфера называется описанной для рассматриваемого многогранника.

Определение 23

Выпуклый многогранник называют описанным, если все его грани касаются сферы. Эта сфера называется вписанной для рассматриваемого многогранника.

Очевидно сходство введённых понятий с известными из курса планиметрии понятиями вписанных и описанных многоугольников, описанных и вписанных окружностей.

Не любой многогранник является вписанным или описанным, однако верны следующие две теоремы, аналогичные соответствующим теоремам про треугольник.

Теорема 3.4 (об описанной сфере треугольной пирамиды)

Треугольная пирамида имеет единственную описанную сферу.

Доказательство. Рассмотрим треугольную пирамиду ABCD (рис. 73). Построим плоскости, перпендикулярные соответственно рёбрам AB, AC и AD и проходящие через их середины. (Геометрическим местом точек пространства, равноудалённых от концов некоторого отрезка, является плоскость, перпендикулярная этому отрезку и проходящая через его середину. Докажите это самостоятельно.) Обозначим через O точку пересечения этих плоскостей. (Такая точка существует, и она единственна. Докажем это. Возьмём первые две плоскости. Они пересекаются, поскольку перпендикулярны непараллельным прямым. Обозначим прямую, по которой пересекаются первые две плоскости, через l. Эта прямая l перпендикулярна плоскости ABC. Плоскость, перпендикулярная AD, не параллельна l и не содержит её, поскольку в противном случае прямая AD перпендикулярна l, т. е. лежит в плоскости ABC.) Точка O равноудалена от точек A и B, A и C, A и D, значит, она равноудалена ото всех вершин пирамиды ABCD, т. е. сфера с центром в O соответствующего радиуса является описанной сферой для пирамиды ABCD.

Итак, мы доказали существование для пирамиды ABCD описанной сферы. Осталось доказать её единственность. Центр любой сферы, проходящей через вершины пирамиды, равноудалён от этих вершин, значит, он принадлежит плоскостям, которые перпендикулярны рёбрам пирамиды и проходят через середины этих рёбер. Следовательно, центр такой сферы совпадает с точкой O.

Теорема доказана. ▼

Отметим, что при этом мы доказали, что все серединные перпендикуляры к рёбрам пирамиды пересекаются в одной точке.

Теорема 3.5 (о вписанной сфере треугольной пирамиды)

У любой треугольной пирамиды существует единственная вписанная сфера.

Доказательство. Рассмотрим треугольную пирамиду ABCD (рис.  74). Проведём биссекторные плоскости  её двугранных углов с рёбрами AB, AC и BC. Эти плоскости имеют единственную общую точку (подумайте почему). Обозначим её через Q. Точка Q равноудалена от всех граней пирамиды. (Она равноудалена от ABC и ABD, ABC и ADC, ABC и CBD.) Значит, сфера соответствующего радиуса с центром в точке Q является вписанной в пирамиду ABCD. Единственность этой сферы доказывается так же, как и в предыдущей теореме. ▼

Как и в предыдущем случае, мы доказали, что все шесть биссекторных плоскостей треугольной пирамиды пересекаются в одной точке.

Замечание. Понятия вписанной и описанной сферы могут относиться также к конусу и цилиндру. Любой конус имеет описанную и вписанную сферы. Если провести осевое сечение конуса, то эта плоскость пересечёт описанную и вписанную сферы по большим окружностям этих сфер, причём получившиеся окружности будут соответственно описаны или вписаны в осевое сечение конуса. Цилиндр, как и конус, всегда имеет описанную сферу. Но в отличие от конуса вписать сферу можно не во всякий цилиндр, а лишь в цилиндр с квадратным осевым сечением.

Задачи, задания, вопросы

1(в). Найдите радиусы описанного и вписанного шаров для правильного тетраэдра с ребром a.

2(в). Найдите ребро куба, вписанного в сферу радиуса R.

3(в). Докажите, что если около параллелепипеда можно описать сферу, то этот параллелепипед — прямоугольный.

4(в). Имеется правильная пирамида со стороной основания a и боковым ребром b. Найдите радиус: а) описанной сферы; б) вписанного шара; в) сферы, касающейся всех рёбер пирамиды; г) сферы, касающейся рёбер основания и продолжений боковых рёбер; д) радиус сферы, которая касается основания и боковых рёбер. Каждый пункт решите для пирамиды следующего вида: 1) четырёхугольной; 2) треугольной; 3) шестиугольной.

5(в). Найдите радиус описанного и вписанного шаров для конуса с радиусом основания r и высотой h.

6.Около шара описаны цилиндр и конус, осевым сечением которого является прямоугольный треугольник. Найдите отношение образующих цилиндра и конуса.

7(в). Найдите радиус сферы, описанной около правильной n-угольной призмы с высотой h и стороной основания a.

8(в). В основании правильной треугольной призмы лежит треугольник со стороной 1. Найдите боковое ребро призмы, если известно, что в неё можно вписать шар.

9(т). Известно, что в заданную призму можно вписать шар. Найдите площадь её боковой поверхности, если площадь основания равна S.

10(т). Плоскость проходит на расстоянии a от центра единичной сферы. Найдите ребро куба, одна грань которого лежит в этой плоскости, а вершины противоположной грани находятся на сфере.

11(в). Около призмы можно описать сферу. Докажите, что основание призмы — многоугольник, около которого можно описать окружность. Найдите радиус этой окружности, если высота призмы h, а радиус описанной около неё сферы равен R.

12(в). Основанием пирамиды служит многоугольник, около которого можно описать окружность. Докажите, что существует сфера, описанная около этой пирамиды. Найдите радиус этой сферы, если радиус окружности, описанной около основания пирамиды, равен r, её высота h, а основание высоты совпадает с вершиной основания пирамиды.

13.В треугольной пирамиде ABCD ребро AB равно a, а углы ACB и ADB — прямые. Найдите радиус описанной около этой пирамиды сферы.

14.Найдите ребро куба, одна грань которого принадлежит основанию конуса, а остальные вершины расположены на его боковой поверхности. Радиус основания конуса равен r, его высота h.

15.Через центр сферы радиуса R проведены три попарно перпендикулярные плоскости. Найдите радиус сферы, касающейся всех этих плоскостей и данной сферы.

16.Осевым сечением конуса является правильный треугольник со стороной a. Через ось конуса проведены две перпендикулярные плоскости, которые делят конус на четыре части. Найдите радиус шара, вписанного в одну из этих частей.

17.Внутри единичного куба находятся восемь равных шаров. Каждый шар вписан в один из трёхгранных углов куба и касается трёх шаров, соответствующих соседним вершинам. Найдите радиусы этих шаров.

18(в). Четыре сферы радиуса R попарно касаются друг друга. Найдите радиус сферы, касающейся всех четырёх сфер.

19.Два шара касаются друг друга и граней трёхгранного угла, все плоские углы которого прямые. Найдите отношение радиусов этих шаров.

20(п). Докажите, что если в данный четырёхгранный угол можно вписать шар, то суммы противоположных плоских углов этого четырёхгранного угла равны. Докажите справедливость обратного утверждения: если суммы противоположных плоских углов четырёхгранного угла равны, то в него можно вписать шар.

21(п). Дан трёхгранный угол OABC, в котором ∠BOC = a, ∠COA = b, ∠  AOB = g. Пусть вписанный в него шар касается грани BOC в точке K. Найдите ∠KOB.

22(т). Треугольник ABC вписан в основание конуса, S — вершина конуса. В трёхгранном угле SABC двугранные углы с рёбрами SA, SB и SC равны соответственно x, y и z. Найдите угол между плоскостями SAB и SAO, где SO — высота данного конуса.

23(т). Четырёхгранный угол OABCD (OA, OB, OC, OD — его рёбра) разделён плоскостью OAC на два трёхгранных угла. В каждый из полученных углов вписан шар. Эти шары касаются плоскости OAC в точках K и M.  Найдите угол KOM, если ∠BOA = a, ∠DOA = b, ∠BOC = ∠COD.

24(п). Докажите, что радиус шара, проходящего через точки пересечения медиан граней произвольного тетраэдра, в три раза меньше радиуса описанного около рассматриваемого тетраэдра шара. Используя этот факт, докажите, что в произвольном тетраэдре выполняется неравенство R ⩾ 3r, где R и r — соответственно радиусы описанного и вписанного шаров.

25(т). Боковое ребро правильной четырёхугольной пирамиды равно l, а плоский угол при вершине равен a. Найдите радиус описанной около этой пирамиды сферы.

Призма вписана в шар, если все ее вершины лежат на поверхности шара (на сфере). В этом случае также говорят, что шар описан около призмы (или сфера описана около призмы).

Призма может быть вписана в шар тогда и только тогда, когда

1) призма  прямая;

2) около ее основания можно описать окружность.

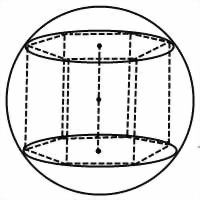
Отсюда следует, что в шар может быть вписана прямая треугольная призма, правильная призма.

Поскольку четырехугольник может быть вписан в окружность, если сумма его противолежащих углов равна 180º, то прямая четырехугольная призма может быть вписана в шар только при выполнении этого условия.

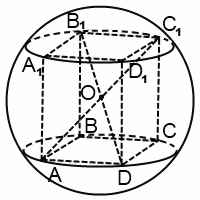
В частности, из параллелепипедов описать шар можно только около прямоугольного параллелепипеда. Центр шара в этом случае — точка пересечения диагоналей параллелепипеда.

В общем случае центр описанного около призмы шара лежит на середине высоты призмы, проходящей через центры описанных около ее оснований окружностей. Центр описанного шара может находиться внутри призмы, вне призмы а также на ее боковой грани.

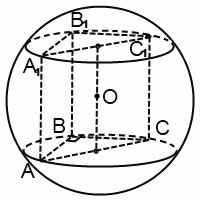
Например, для треугольной призмы, в которой угол ABC — прямой, центр описанного шара лежит на боковой грани, на высоте, соединяющей середины гипотенуз в основаниях призмы.

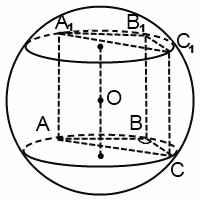
Если угол ABC — тупой, то центр описанного около треугольной призмы шара находится вне призмы.

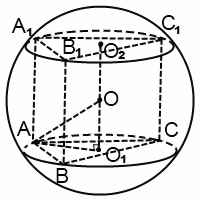Рассмотрим прямоугольный треугольник AOO1. O1O2=H — высота призмы, AO=R — радиус шара, AO1=r — радиус окружности, описанной около основания призмы. По теореме Пифагора