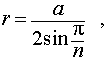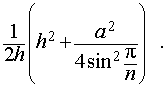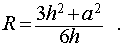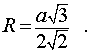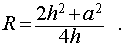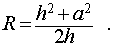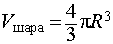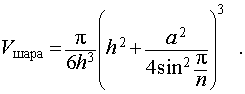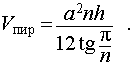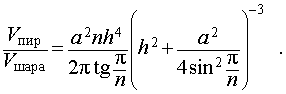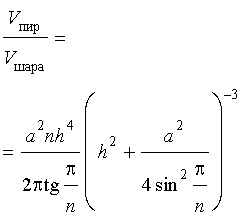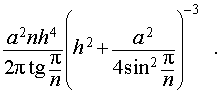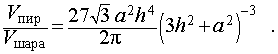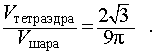Как найти радиус сферы описанной около тетраэдра

Радиус описанной сферы тетраэдра

Свойства

Зная радиус сферы, описанной около тетраэдра, нужно, во-первых, найти ребро тетраэдра, а также можно узнать сразу радиус сферы, вписанной в тетраэдр, так как он ровно в три раза меньше радиуса описанной окружности. a=(2√6 R_1)/3 r_1=R_1/3

Затем, зная ребро тетраэдра через радиус сферы, описанной около тетраэдра, можно найти его периметр, который представляет собой длину всех ребер тетраэдра, площадь одной грани и площадь полной поверхности тетраэдра, состоящей из четырех граней. P=4√6 R_1 S_1=2√3 〖R_1〗^2 S_(п.п.)=4S_1=8√3 〖R_1〗^2

Помимо радиусов вписанной и описанной около тетраэдра сфер, тетраэдр также обладает радиусами вписанной и описанной окружностей около основания, являющимся одной из граней, которые можно вычислить через радиус описанной сферы. r=(√2 R_1)/3 R=(2√2 R_1)/3

Чтобы найти высоту тетраэдра, нужно умножить радиус описанной вокруг него сферы на четыре и разделить на три, а чтобы вычислить апофему тетраэдра через радиус описанной сферы, необходимо умножить его на корень из двух. h=(4R_1)/3 l=√2 R_1

Объем тетраэдра, зная радиус сферы, описанной около него, равен радиусу в кубе, умноженному на коэффициент восемь корней из трех, деленный на три.. V=(8√3 〖R_1〗^3)/3

Пирамида, вписанная в сферу

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

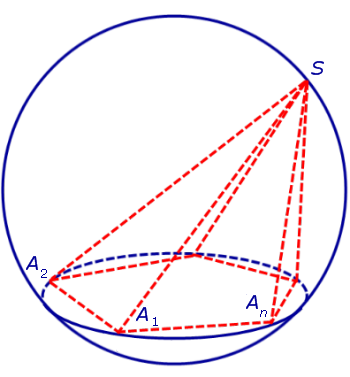
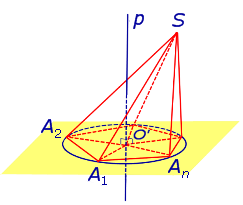
Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.

Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

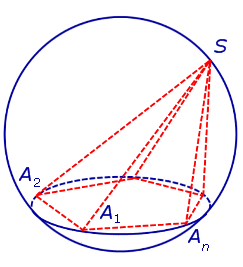
Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

На рисунке 2 изображена пирамида SA₁A₂ . A_n , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A₁A₂ . A_n – основание пирамиды. Доказано.

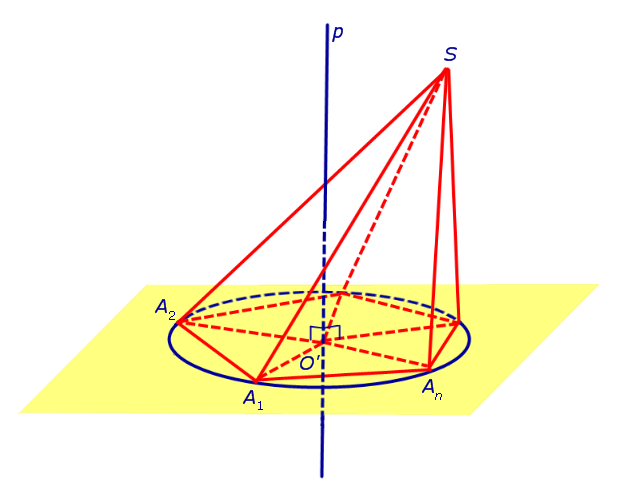
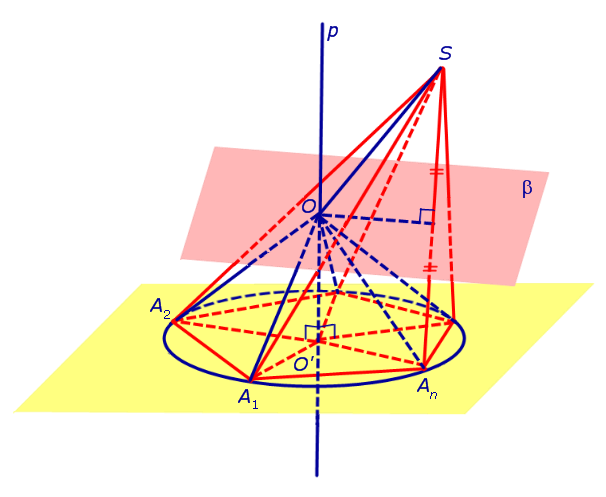
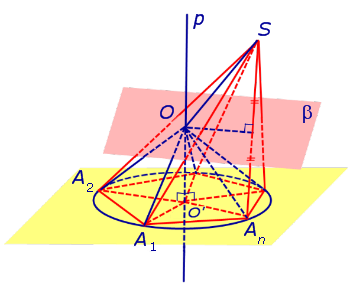
Теперь предположим, что около основания A₁A₂ . A_n пирамиды SA₁A₂ . A_n можно описать окружность. Докажем, что в этом случае около пирамиды SA₁A₂ . A_n можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A₁A₂ . A_n , символом O’ и проведем прямую p, проходящую через точку O’ и перпендикулярную к плоскости многоугольника A₁A₂ . A_n (рис. 3).

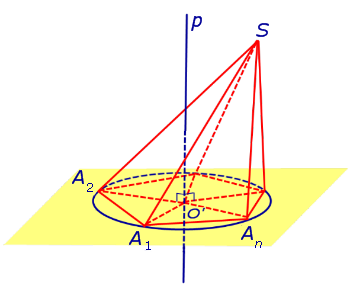
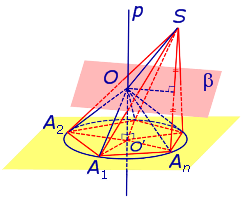
Рассмотрим плоскость β, проходящую через середину отрезка SA_n и перпендикулярную к этому отрезку. Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA₁A₂ . A_n . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.

Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA₁A₂ . A_n . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA₁A₂ . A_n .

Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A₁A₂ . A_n , что противоречит определению пирамиды.

Следствие 1. Около любой правильной пирамиды можно описать сферу.

Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.

Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.

Радиус сферы, описанной около правильной n – угольной пирамиды

Задача 1. Высота правильной n – угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.

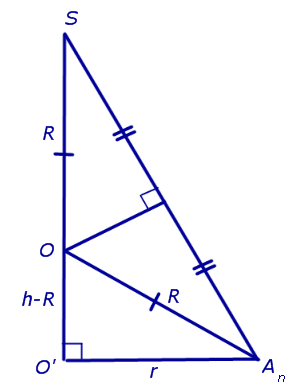
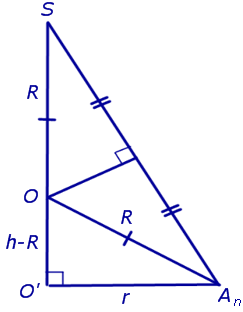
Решение. Рассмотрим правильную n – угольную пирамиду SA₁A₂ . A_n и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’A_n (рис. 5).

Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OA_n получаем

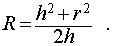(1)

из формулы (1) получаем соотношение

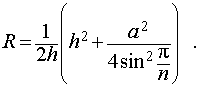(2)

Ответ.

Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен

Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен

Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен

Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен

Отношение объемов правильной n – угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Задача 2. Около правильной n – угольной пирамиды с высотой h и ребром основания a описана сфера. Найти отношение объемов пирамиды и шара, ограниченного сферой, описанной около данной пирамиды.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около пирамиды сферой, через высоту и ребро основания пирамиды:

Ответ.

Следствие 7. Отношение объема правильной треугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной пирамиды, равно

Следствие 8. Отношение объема правильного тетраэдр с ребром a к объему шара, ограниченного сферой, описанной около данного тетраэдра, равно

Следствие 9. Отношение объема правильной четырехугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 10. Отношение объема правильной шестиугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Тетраэдр.

Тетраэдр – это частный случай правильной треугольной пирамиды.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Медиана тетраэдра – это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).

Бимедиана тетраэдра – это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).

Высота тетраэдра – это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Типы тетраэдров.

Правильный тетраэдр – это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Правильный тетраэдр – это один из 5-ти правильных многогранников.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

– Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

– Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

– Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

– Каркасный тетраэдр — тетраэдр, который таким условиям:

• есть сфера, которая касается каждого ребра,
• суммы длин ребер, что скрещиваются равны,
• суммы двугранных углов при противоположных ребрах равны,
• окружности, которые вписаны в грани, попарно касаются,
• каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
• перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.

– Соразмерный тетраэдр, бивысоты у него одинаковы.

– Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

Формулы для определения элементов тетраэдра.

Высота тетраэдра:

где h – высота тетраэдра, a – ребро тетраэдра.

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

где V – объем тетраэдра, a – ребро тетраэдра.

Основные формулы для правильного тетраэдра:

Где S – Площадь поверхности правильного тетраэдра;

h – высота, опущенная на основание;

r – радиус вписанной в тетраэдр окружности;

[spoiler title=”источники:”]

http://www.resolventa.ru/spr/stereometry/piramide_sphere.htm

http://www.calc.ru/1535.html

[/spoiler]

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

• Формулы расчета радиуса сферы (шара)
  • Правильная треугольная пирамида
  • Правильная четырехугольная пирамида

  • Правильная шестиугольная пирамида

Формулы расчета радиуса сферы (шара)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

• a – ребро основания пирамиды;
• h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

Координаты центра описанной вокруг тетраэдра сферы.
Радиус описанной вокруг тетраэдра сферы.

Пусть A(xa, ya, za), B(xb, yb, zb), C(xc, yc, zc), S(xs, ys, zs) – вершины тетраэдра,
bgColor=”#F0E68C”
O(xo, yo, zo) – центр описанной вокруг тетраэдра SABC сферы радиуса R

Из второго, третьего и четвёртого уравнения вычистаем первое:

По формулам Крамера:

В знаменателе стоит отличное от нуля смешанное произведение векторов AS, BS, CS, равное по модулю утроенному объёму данного тетраэдра SABC. Поэтому у данной системы сущестует единственное решение.

Центр описанной вокруг тетраэдра сферы имеет координаты:

Радиус описанной сферы:

На главную страницу.

Зная радиус сферы, описанной около тетраэдра, нужно, во-первых, найти ребро тетраэдра, а также можно узнать сразу радиус сферы, вписанной в тетраэдр, так как он ровно в три раза меньше радиуса описанной окружности.
a=(2√6 R_1)/3
r_1=R_1/3

Затем, зная ребро тетраэдра через радиус сферы, описанной около тетраэдра, можно найти его периметр, который представляет собой длину всех ребер тетраэдра, площадь одной грани и площадь полной поверхности тетраэдра, состоящей из четырех граней.
P=4√6 R_1
S_1=2√3 〖R_1〗^2
S_(п.п.)=4S_1=8√3 〖R_1〗^2

Помимо радиусов вписанной и описанной около тетраэдра сфер, тетраэдр также обладает радиусами вписанной и описанной окружностей около основания, являющимся одной из граней, которые можно вычислить через радиус описанной сферы.
r=(√2 R_1)/3
R=(2√2 R_1)/3

Чтобы найти высоту тетраэдра, нужно умножить радиус описанной вокруг него сферы на четыре и разделить на три, а чтобы вычислить апофему тетраэдра через радиус описанной сферы, необходимо умножить его на корень из двух.
h=(4R_1)/3
l=√2 R_1

Объем тетраэдра, зная радиус сферы, описанной около него, равен радиусу в кубе, умноженному на коэффициент восемь корней из трех, деленный на три..
V=(8√3 〖R_1〗^3)/3

Instead of tetrahedron, let us work out a general formula for $n$-simplex first.

Given any non-degenerate $n$-simplex $S$ with vertices $v_1, ldots, v_{n+1}$. Let

• $V$ be the volume of $S$.
• $ell_{ij} = | v_i – v_j |$ be the edge lengths.
• $c$ and $R$ be the center and radius for the circumsphere.
• $lambda_1, ldots, lambda_{n+1}$ be the barycentric coordinates of $c$ with respect to $S$.
  i.e the list of $n+1$ real numbers such that
  $$c = sum_{i}lambda_i v_iquadtext{ with }quad sum_{i}lambda_i = 1$$

Recall for any two points $u, v$ with barycentric coordinates $mu_i, nu_i$ with respect to $S$.
Their distance is given by the formula:

$$| u – v |^2 = -sum_{i < j}ell_{ij}^2(mu_i – nu_i)(mu_j – nu_j)$$

Apply this to circumcenter $c$ and vertex $v_k$, we obtain

$$R^2 = -sum_{i<j}ell_{ij}^2 (lambda_i – delta_{ki})(lambda_j – delta_{kj}) = sum_{j}ell_{kj}^2 lambda_j – frac12 sum_{i,j} ell_{ij}^2lambda_ilambda_j$$
Multiply by $lambda_k$ and sum over $k$, we obtain

$$R^2 = frac12sum_{i,j} ell_{ij}^2 lambda_ilambda_j
quadimpliesquad
2R^2 = sum_{j}ell_{kj}^2 lambda_j;;text{ for all }ktag{*1}$$

To proceed, rewrite everything in matrix form. Let

• ${bf theta}$ be the $(n+1)times 1$ column vector with all entries $1$.
• ${bf lambda}$ be the $(n+1)times 1$ column vector with entries $lambda_i$.
• $Lambda$ be the $(n+1)times(n+1)$ matrix with entries $ell_{ij}^2$.
• $Delta$ be the $(n+2)times(n+2)$ matrix
  $begin{bmatrix}0 & {bf theta}^T \ {bf theta} & Lambdaend{bmatrix}$

In terms of them, $(*1)$ becomes $2R^2{bf theta} = Lambda {bf lambda}$.

Together with ${bf theta}^T{bf lambda} = sum_{i} lambda_i = 1$, we obtain

$$Delta begin{bmatrix} -2R^2 \ {bf lambda}end{bmatrix}
= begin{bmatrix}0 & {bf theta}^T \ {bf theta} & Lambdaend{bmatrix}
begin{bmatrix} -2R^2 \ {bf lambda}end{bmatrix}
= begin{bmatrix} 1 \ 0end{bmatrix}
quadimpliesquad
begin{bmatrix} -2R^2 \ {bf lambda}end{bmatrix} = Delta^{-1}begin{bmatrix} 1 \ 0end{bmatrix}
$$
Extracting the first component of both sides and notice $Delta^{-1} = (detDelta)^{-1} {rm adj}Delta$, we get
$$-2R^2 = frac{detLambda}{detDelta}$$

Notice $detDelta$ is simply the Cayley-Menger determiant for $S$ which satisfies
$$V^2 = frac{(-1)^{n+1}}{2^n n!^2} detDelta$$
This means the volume $V$, the circumradius $R$ and $detLambda$ of a $n$-simplex are related by following formula:

$$bbox[border:1px solid blue;padding: 16px;]{(-1)^n 2^{n+1}(n!)^2 (VR)^2 = detLambda}tag{*2}$$

For example, when $n = 2$, the $n$-simplex becomes a triangle. If $a, b, c$ are
the side lengths of a triangle. $(*2)$ reduces to the familiar relation among its area, circumradius and side lengths.

$$32V^2R^2 = det
begin{bmatrix}
0 & a^2 & b^2\
a^2 & 0 & c^2\
b^2 & c^2 & 0
end{bmatrix}
= 2a^2b^2c^2
quadiffquad
4VR = abc
$$

Back to the original problem of tetrahedron which corresponds to $n = 3$.
Let $a, b, c$ be the lengths of the three edges attached to a vertex. Let $a_1, b_1, c_1$ be the lengths of corresponding opposite edges. $(*2)$ becomes
$$-576(VR)^2 =
detbegin{bmatrix}
0 & a^2 & b^2 & c^2\
a^2 & 0 & c_1^2 & b_1^2\
b^2 & c_1^2 & 0 & a_1^2\
c^2 & b_1^2 & a_1^2 & 0
end{bmatrix}
$$
Reproducing the complicated formula appeared in the link in Edward Jiang’s comment.

To simplify further, we first multiply
$2^{nd}/3^{rd}/4^{th}$ row/column of $Lambda$ by $frac{bc}{a}, frac{ac}{b},
frac{ab}{c}$ and then divide the $1^{st}$ row/column or resulting matrix by $abc$. At the end, we find
$$detLambda = detbegin{bmatrix}
0 & 1 & 1 & 1\
1 & 0 & (cc_1)^2 & (bb_1)^2\
1 & (cc_1)^2 & 0 & (aa_1)^2\
1 & (bb_1)^2 & (aa_1)^2 & 0
end{bmatrix}
$$
This has the form of a Cayley-Menger determinant for a “triangle” with sides $aa_1$, $bb_1$ and $cc_1$. Recall Heron’s formula for computing area of triangle, $detLambda$ can be factorized as follows:

$$detLambda = -16 p(p-aa_1)(p-bb_1)(p – cc_1)quadtext{ where }quad p = frac{aa_1 + bb_1 + cc_1}{2}$$

As a result, we obtain a much simpler relation for tetrahedron.

$$bbox[border:1px solid blue;padding: 16px;]{6VR = sqrt{p(p-aa_1)(p-bb_1)(p-cc_1)}}tag{*3}$$

Update

I recently come across an elegant proof of formula $(*3)$ using sphere inversion (the 3d-counterpart of circle inversion in 2d). It explains why the RHS
is the area of a triangle with sides $aa_1$, $bb_1$, $cc_1$.

Let $OABC$ be a tetrahedron with sides $OA = a, OB = b, OC = c, BC = a_1, CA = b_1, AB = c_1$. Let $V$ and $R$ be its volume and circumradius.
Let $A’, B’, C’$ be the image of $A, B, C$ under a sphere inversion with respect to the sphere centered at $O$ with radius $rho = sqrt[3]{abc}$.

Notice tetrahedron $OA’B’C’$ is sharing a trihedral angle at $O$ with $OABC$.
Since
$$|OA’||OB’||OC’| = frac{rho^2}{a}frac{rho^2}{b}frac{rho^2}{c} = abc = |OA| |OB| |OC|$$
The volume of tetrahedron $OA’B’C’$ also equals to $V$.

Under the sphere inversion, the circumsphere of $OABC$ get mapped at a plane at a distance $frac{rho^2}{2R}$ from $R$. The points $A’$, $B’$, $C’$ belong to this plane and they are forming a triangle with sides $B’C’ = frac{a_1rho^2}{bc}, C’A’ = frac{b_1rho^2}{ac}, A’B’ = frac{c_1rho^2}{ab}$. If $Delta(u,v,w)$ is the area of a triangle of sides $u,v,w$, then
$$V = frac{1}{3}frac{rho^2}{2R}Deltaleft(
frac{a_1rho^2}{bc},
frac{b_1rho^2}{ac},
frac{c_1rho^2}{ab}
right)
= frac{1}{6R}
Deltaleft(
frac{a_1rho^3}{bc},
frac{b_1rho^3}{ac},
frac{c_1rho^3}{ab}
right)
= frac{1}{6R}
Delta(aa_1,bb_1,cc_1)
$$
Together with Heron’s formula, $(*3)$ follows.