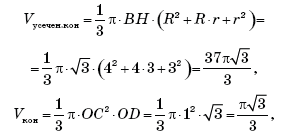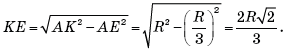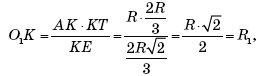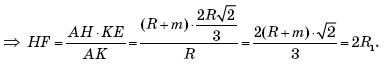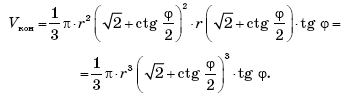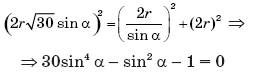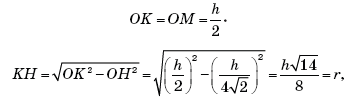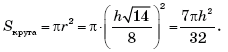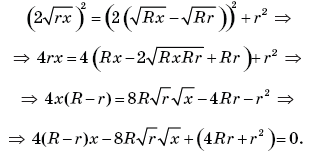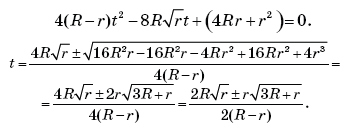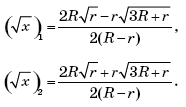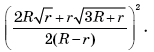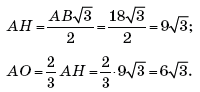Как найти радиус сферы в усеченном конусе

Пирамида, вписанная в конус

Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды.

Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Упражнение 1

Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Ответ:

Упражнение 2

Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Ответ:

Упражнение 3

Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Ответ: 1.

Пирамида, описанная около конуса

Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду.

В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.

Упражнение 1

Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Ответ:

Упражнение 2

Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Ответ: 2.

Упражнение 3

Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Ответ:

Сфера, вписанная в конус

Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы.

В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса.

Напомним, что радиус r окружности, вписанный в треугольник, находится по формуле

где S – площадь, p – полупериметр треугольника.

Упражнение 1

В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.

Решение. Треугольник SAB равносторонний. Высота SH равна Площадь S равна Полупериметр p равен 3. По формуле r = S/p получаем

Упражнение 2

В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.

Решение. Обозначим h высоту SH конуса . Из формулы r = S/p имеем:

где r = 1, a = FG = 4, p =

Решая уравнение

находим

Упражнение 3

Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус вписанной сферы.

Решение. Высота SH конуса равна 1. Образующая .

Полупериметр p равен

По формуле r = S/p , имеем

Ответ:

Упражнение 4

Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.

Решение. Радиус основания конуса равен 6. Площадь треугольника SFG равна 48, полупериметр 16. По формуле r = S/p имеем r = 3.

Ответ: r = 3.

Упражнение 5

Можно ли вписать сферу в наклонный конус?

Ответ: Нет.

Сфера, вписанная в усеченный конус

Сфера называется вписанной в усеченный конус, если она касается его основани й и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы.

В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.

Упражнение 1

В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.

Решение. Имеем: A 1 B = A 1 O 1 = 2, A 2 B = A 2 O 2 = 1. Следовательно, A 1 A 2 = 3 , A 1 C = 1.

Таким образом,

Упражнение 2

В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания.

Решение. Пусть A 1 O 1 = 2. Обозначим r = A 2 O 2 . Имеем: A 1 A 2 = 2+ r , A 1 C = 2 – r . По теореме Пифагора, имеет место равенство из которого следует, что выполняется равенство Решая полученное уравнение относительно r , находим

Упражнение 3

В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60 о . Найдите радиус вписанной сферы.

Решение. Заметим, что осевым сечением конуса, из которого получен усеченный конус, является равносторонний треугольник со стороной 2. Радиус r сферы, вписанной в усеченный конус, равен радиусу окружности, вписанной в этот равносторонний треугольник, т.е.

Упражнение 4

Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы.

Решение. Воспользуемся формулой r = S/p , где S – площадь осевого сечения, p – полупериметр. В нашем случае S = 3 . Для нахождения полупериметра напомним, что для четырехугольника, описанного около окружности, суммы противоположных сторон равны. Значит, полупериметр равен удвоенной образующей цилиндра, т.е. p = 4. Следовательно, r = ¾.

Ответ:

Упражнение 5

Можно ли вписать сферу в усеченный наклонный конус.

Ответ: Нет.

Сфера, описанная около конуса

Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу .

Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса.

Напомним, что радиус R окружности, описанной около треугольника, находится по формуле

где S – площадь, a , b , c – стороны треугольника.

Упражнение 1

Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.

Решение. Треугольник SAB равносторонний со стороной 2. Высота SH равна Площадь S равна По формуле R = abc /4 S получаем

Упражнение 2

Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.

Решение. Имеем, OB = 5 , HB = 4. Следовательно, OH = 3. Учитывая, что SO = OB = 5, получаем h = 8.

Ответ: h = 8.

Упражнение 3

Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус описанной сферы.

Решение. Треугольник SAB – прямоугольный, равнобедренный. Следовательно, радиус R описанной сферы равен радиусу основания цилиндра, т.е. R = 1.

Ответ: R = 1.

Упражнение 4

Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.

Решение. В треугольнике SAB имеем: SA = SB = 10, SH = 8. По теореме Пифагора, AH = 6 и, следовательно, S = 48. Используя формулу R = abc /4 S , получаем

Упражнение 5

Можно ли описать сферу около наклонного конуса?

Ответ: Да.

Сфера, описанная около усеченного конуса

С фера называется описанной около усеченного конуса, если окружност и основани й усеченного конуса лежат на сфере. При этом усеченный к онус называется в писанным в сферу.

Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы.

Упражнение 1

Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.

Решение. Заметим, что A 1 O 1 B 2 O 2 и O 1 B 1 B 2 A 2 – ромбы. Треугольники A 1 O 1 A 2 , O 1 A 2 B 2 , O 1 B 1 B 2 – равносторонние и, значит, A 1 B 1 –диаметр. Следовательно, R = 2.

Ответ: R = 2,

Упражнение 2

Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45 о с плоскостью другого основания. Найдите радиус описанной сферы.

Решение. Имеем A 2 O 2 = 1, A 1 A 2 = 2, O 1 O 2 = , OO 1 = O 1 C = 1. Следовательно, OO 2 = 1 + и, значит,

Упражнение 3

Радиус одного основания усеченного конуса равен 4, высота 7, радиус описанной сферы 5. Найдите радиус второго основания усеченного конуса.

Решение. Имеем OO 1 = 3 , OO 2 = 4 и, следовательно, O 2 A 2 = 3.

Ответ: 3.

Упражнение 4

Найдите радиус сферы, описанной около усеченного конуса, радиусы оснований которого равны 2 и 4, а высота равна 5.

Решение. Обозначим R радиус описанной сферы. Тогда

Учитывая, что O 1 O 2 = 6, имеем равенство

Решая его относительно R , находим

Упражнение 5

Можно ли описать сферу около усеченного наклонного конуса.

Ответ: Нет.

Условие

Решение

Написать комментарий

Комбинации тел вращения

Конус и усеченный конус

Следует объяснить учащимся, что при решении различных задач
на комбинацию конуса и усеченного конуса достаточно изобразить их сечение
плоскостью, проходящей через ось конуса. В таком случае решение
стереометрической задачи сводится к решению задачи планиметрической на
комбинацию трапеции и треугольника.

Задача 1.  Трапеция со сторонами 2, 2, 2 и 4 вращается
вокруг прямой, лежащей в плоскости трапеции и проходящей через одну из вершин
большего основания перпендикулярно этому основанию. Найдите объем тела вращения.

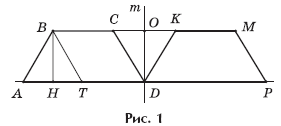
Решение. Пусть трапеция ABCD, у которой AB
= BC = CD = 2, AD = 4, вращается вокруг прямой m,
проходящей через вершину D перпендикулярно основанию AD. На
рисунке 1 изображено осевое сечение полученного тела вращения (плоскость сечения
проходит через ось вращения m). Это сечение состоит из двух равных и
симметричных относительно прямой m трапеций ABCD и PMKD,
которые равными прямоугольными треугольниками COD и KOD (O
= m ∩ BC)
дополняются до равных прямоугольных трапеций ABOD и PMOD. Это
означает, что объем тела, полученного при вращении трапеции ABCD, равен
разности объема усеченного конуса, полученного при вращении прямоугольной
трапеции ABOD вокруг прямой m, и объема конуса, полученного при
вращении прямоугольного треугольника COD вокруг прямой m. Найдем
объем тела вращения.

Высота конусов равна OD. Отрезки BO = r
и AD = R являются радиусами соответственно верхнего и нижнего
оснований усеченного конуса, а отрезок OC — радиус основания прямого
кругового конуса с вершиной D. Найдем объемы этих конусов.

Проведем отрезок BT параллельно CD. Тогда из
равенств BT = CD = AB = BC и BC = TD
следует, что AB = BT = AT, откуда треугольник ABT —
правильный, в котором

При этом BM = 3BC = 6 (CK = AT =
BC), значит,

(OD — серединный перпендикуляр BM). Тогда

и искомый объем тела вращения равен

Ответ:  куб. ед.

Сферы, шары и конус

Перед решением задач на комбинацию сферы и конуса следует
повторить планиметрический материал о комбинациях окружности и равнобедренного
треугольника.

Во многих случаях решение задачи упрощается, если
использовать сечения комбинации сферы и конуса диаметральной плоскостью сферы,
содержащей ось конуса. В результате решение данной стереометрической задачи
сводится к решению задачи планиметрической на комбинацию окружности и
равнобедренного треугольника.

Задача 2.  В конус помещены две сферы. Одна из этих сфер
вписана в конус, а вторая касается первой сферы и конической поверхности, имея с
ней общую окружность. Найдите отношение радиусов первой и второй сфер, если
образующая конуса в три раза больше радиуса его основания.

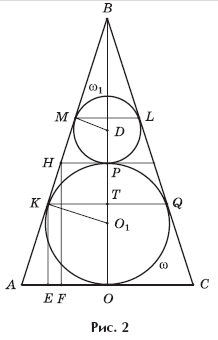
Решение. Рассмотрим сечение комбинации данных конуса и
двух сфер плоскостью, проходящей через ось конуса (рис. 2). Сечением конуса
является равнобедренный треугольник ABC
(AB = BC, BO AC), в котором OA = R (R — радиус основания конуса);
сечением сферы, вписанной в конус, — окружность
ω с центром O₁,
вписанная в треугольник ABC и касающаяся его сторон в точках K,
Q и O (KQ AC); сечением второй сферы — окружность
ω₁, касающаяся
окружности ω в точке
P и боковых сторон треугольника ABC — в точках M и L
(P — точка касания сфер, ML — диаметр окружности касания этой
сферы с боковой поверхностью конуса).

Обозначим:
O₁K = R₁ —
радиус окружности ω
(радиус первой сферы),
O₁K
 AB; DM = r — радиус окружности ω₁
(радиус второй сферы), DM AB.

Проведем: KE
AC; HF
AC; PH
AC (PH —
общая касательная окружностей ω
и ω₁).

Из условия следует: AB = 3R. Имеем: AK =
AO = R
(как отрезки касательных к окружностиω),
значит, AK : AB = R : 3 R = 1 : 3.

Так как BO
AC,KE AC,
то KE
BO. По теореме Фалеса получим:

AE: AO = AK : AB = 1 : 3,

откуда Тогда в прямоугольном треугольнике AKE

Кроме того,

Так как KQ AC, BO AC, то KQ BO. Далее, O₁K
AB (как радиус,
проведенный в точку касания). Значит,  AKE
=  O₁KT
(как углы с соответственно перпендикулярными сторонами). Тогда прямоугольные
треугольники AKE и O₁KT подобны, поэтому AK
: O₁K = KE : KT, откуда

значит,

Найдем иначе длину OP = HF.

Пусть KH = m. Имеем: HK = HP, а
HP = HM (как отрезки касательных к окружностям
ω и
ω₁), отсюда KM
= 2m, AH = R + m. Тогда из подобия прямоугольных
треугольников AKE и AHF получаем:

AK : AH = KE : HF

Из равенства находим: 2m = R
m = 0,5R.

Значит, KM = 2m = 20,5R
= R.
Поэтому BM = BK – KM = 2R – R = R.
Тогда из подобия прямоугольных треугольников BO₁K и
BDM имеем:

R ₁ : r = O₁K :
DM = BK : BM = 2R : R = 2 : 1.

Ответ: 2 : 1.

Задача 3. Внутри конуса расположены четыре равных шара
радиуса r так, что каждый из них касается двух других шаров, основания
конуса и его боковой поверхности. Найдите объем конуса, если его образующие
наклонены к плоскости основания под углом j.

Решение. Пусть PO — высота данного конуса (точка
O — центр его основания); точки A, B, C, D —
центры данных шаров. Так как все шары равны и каждый из них касается основания
конуса, то центры A, B, C, D этих шаров равноудалены
от плоскости основания конуса и расположены в плоскости, параллельной основанию
конуса и удаленной от нее на расстояние R.

По условию задачи каждый из шаров касается двух других шаров.
Поэтому AB = BC = CD = DA = 2r
(точка касания двух шаров лежит на линии их центров), откуда следует, что
четырехугольник ABCD — ромб. Вследствие равенства шаров AC = BD.
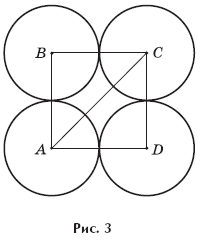
Значит, ABCD — квадрат со стороной 2r и расстояние между центрами
A и C «противоположных» (не касающихся) шаров равно (как диагональ
квадрата). (На рисунке 3 изображено сечение шаров плоскостью, проходящей через
их центры.)

Плоскость, проведенная через высоту конуса, перпендикулярна
основанию конуса и пересекает это основание по его диаметру. Поэтому проекция
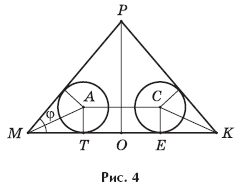
образующей конуса расположена на диаметре его основания, значит, угол
j между образующей конуса и
плоскостью его основания равен углу между этой образующей и диаметром основания,
проведенным через основание образующей (рис. 4).

Проведем плоскость α = (PAC) через ось OP конуса. В пересечении этой плоскости с
конусом получается равнобедренный треугольник PMK (PM = PK
как образующие конуса). А так как шары касаются боковой поверхности конуса, то
пересечением плоскости a
с шарами, имеющими центры A и C, являются два круга радиуса r
с теми же центрами, вписанные в углы PMK и PKM, при этом точки
A и C расположены на биссектрисах этих углов (см. рис. 4). В
треугольнике PMK высота PO равна высоте h конуса, а
основание MK — диаметру основания конуса, то есть MK = 2R,
где R — радиус основания конуса.

Для вычисления объема конуса воспользуемся формулой Найдем
высоту h конуса и радиус R.

Пусть T и E — точки, в которых круги с центрами
A и C касаются основания MK треугольника PMK (в
точках T и E шары с центрами A и C касаются
основания конуса).
Тогда AT MK и CE MK, при этом AT = CE = r, значит,

В прямоугольном треугольнике MAT

находим:

Вследствие симметрии равнобедренного треугольника PMK
относительно PO имеем:

тогда

В прямоугольном треугольнике OMP:

Тогда

Ответ:

Шары и усеченный конус

Решение задачи на комбинацию шара и усеченного конуса
упрощается, если использовать сечение комбинации шара и усеченного конуса
диаметральной плоскостью шара, содержащей ось конуса. В таком случае решение
данной стереометрической задачи сводится к решению планиметрической задачи на
комбинацию круга и равнобедренной трапеции.

Задача 4.  Радиус сферы, вписанной в усеченный конус,
равен r, радиус сферы, описанной около этого усеченного конуса, равен
Найдите угол между образующей усеченного конуса и его основанием.

Решение. Окружности оснований данного усеченного конуса —
это сечения параллельными плоскостями сферы с центром B и радиусом Так
как центр любой окружности, расположенной на сфере, принадлежит прямой,
проходящей через центр сферы и перпендикулярной плоскости этой окружности, то
центры O и T оснований усеченного конуса и центр B сферы
лежат на одной прямой, перпендикулярной плоскостям оснований этого конуса. На
этой же прямой расположен и центр A сферы, вписанной в усеченный конус,
так как вписанная в усеченный конус сфера касается его оснований в их центрах
O и T.

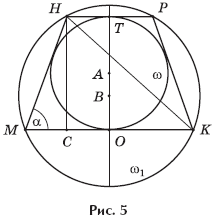
На рисунке 5 изображено сечение комбинации усеченного конуса
и двух данных сфер плоскостью, проходящей через центр B сферы
перпендикулярно плоскостям оснований усеченного конуса: в сечении конуса этой
плоскостью получается равнобедренная трапеция MHPK, а сечениями сфер
являются две окружности ω и ω₁
радиусов r и с центрами соответственно A и B, одна из которых
вписана в трапецию MHPK, а другая описана около нее.

Пусть HC — высота усеченного конуса (высота трапеции)
и α — угол наклона его
образующей MH к плоскости нижнего основания (угол при вершине нижнего
основания трапеции).

Выразим дважды длину диагонали HK через r и
a. С одной стороны, в
треугольнике MKH имеем:

С другой стороны, в треугольнике HCK ( HCK
=90°)
по теореме Пифагора находим:

HK² = CK² + CH².
(*)

Выразим CH и CK через r и
α.

Трапеция MHPK описана около окружности с центром A
и радиусом r, поэтому HC = 2r и
HP + MK = 2MH
(суммы противоположных сторон четырехугольника, описанного около окружности,
равны), откуда Кроме того, трапеция MHPK — равнобедренная, значит,
Следовательно, CK = MH.

В прямоугольном треугольнике MCH находим: Тогда
Подставив в (*)
вместо HK, CK и CH их выражения через r и
α, получаем:

(sin α ≠ 0, так как α ≠ 0).

Сделав подстановку sin² α
= t (0 < t < 1), получаем: 30t² – t – 1 =
0.

Находим:

(не удовлетворяет t > 0), t₂ = 0,2.
Тогда

sin² α
= 0,2 cos² α
= 0,8

cos 2α = 0,6 2α = arccos 0,6

α = 0,5arccos 0,6.

Таким образом,  M
=  K =
0,5arccos 0,6.

Ответ: 0,5arccos 0,6.

Сферы, шар и цилиндр

Перед решением задач на комбинацию сферы и цилиндра следует
повторить планиметрический материал о комбинациях окружности и прямоугольника
(квадрата), о комбинациях двух касающихся, пересекающихся и не имеющих общих
точек окружностей. Учащимся необходимо знать, что в цилиндр можно вписать сферу
тогда и только тогда, когда цилиндр равносторонний, так как диаметр сферы,
вписанной в цилиндр, равен высоте (образующей) этого цилиндра.

При решении задач на комбинацию сферы (шара) и цилиндра
совершенно не обязательно изображать сферу и цилиндр, а достаточно рассмотреть
сечение этой комбинации пространственных фигур плоскостью. Во многих случаях
решение задачи упрощается, если использовать сечения сферы (шара) и цилиндра
диаметральной плоскостью сферы (шара), содержащей ось цилиндра (параллельной
этой оси), или диаметральной плоскостью сферы (шара), перпендикулярной оси
цилиндра.

Задача 5.  Плоскость α,
образующая с осью цилиндра угол в 45°,
делит ось в отношении 1 : 3. Найдите площадь круга, по которому эта плоскость
пересекает шар, вписанный в цилиндр, если высота цилиндра равна h.

Решение. Пусть MT — ось данного цилиндра, точка
O — центр вписанного в него шара, O
MT.

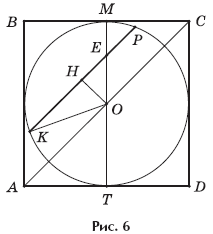
Рассмотрим сечение цилиндра и вписанного в него шара
плоскостью, проходящей через ось MT. В сечении получаем соответственно
квадрат ABCD и круг с центром O, вписанный в этот квадрат
(рис. 6). (Осевым сечением любого цилиндра является прямоугольник, но в данном
случае сечением цилиндра может быть только квадрат, так как в прямоугольник
нельзя вписать окружность.)

Касательная прямая m в точке A к окружности
нижнего основания цилиндра, расположенная в плоскости этого основания,
перпендикулярна диаметру AD. А так как AD — проекция AC на
эту плоскость, то AC m (по теореме о трех перпендикулярах). Тогда угол CAD — линейный
угол двугранного угла, образованного плоскостью основания цилиндра и плоскостью
β, проходящей через
AC и m, причем β (ABC) (по
признаку перпендикулярности двух плоскостей) и AC = β ∩ (ABC).
Поэтому ортогональной проекцией оси MT на плоскость
β является прямая AC,
следовательно,  COM = 45° — угол между
осью MT и плоскостью β.

Так как  CAD
= 45° (в квадрате
ABCD), то плоскость β наклонена к плоскости основания цилиндра под углом 45°
и образует с осью MT угол в 45°.

Это означает, что α β.

Далее, пусть точка E делит ось MT в отношении
ME : ET = 1 : 3, значит, ME : MT = 1 : 4.
Тогда Так
как α β, то плоскость
α проходит через точку E
и пересекает плоскость ABC осевого сечения цилиндра по прямой,
параллельной AC. Обозначим: KP — отрезок пересечения этой прямой и
круга — сечения шара плоскостью ABC; длина отрезка KP равна
диаметру круга, по которому плоскость α пересекает шар. Проведем OH B
KP, тогда HK = r — радиус этого круга. Найдем r.
Имеем:

KP AC COM =
MEP =
HEO = 45°,

тогда в равнобедренном прямоугольном треугольнике EOH

В прямоугольном треугольнике KOH

где r — радиус круга — сечения шара плоскостью
α.

Находим площадь этого круга:

Ответ:   кв. ед.

Задача 6.  В цилиндр помещены четыре попарно касающиеся
сферы радиуса R = 3 так, что каждая сфера касается данной цилиндрической
поверхности. При этом две сферы касаются нижнего, а две другие — верхнего
оснований цилиндра. Найдите объем этого цилиндра.

Решение. Пусть P и A — центры сфер,
касающихся верхнего основания цилиндра, B и C — центры сфер,
касающихся его нижнего основания. Тогда точки P и A равноудалены
от верхнего, а точки B и C — от нижнего основания на расстояния,
равные 3. Поэтому прямые AP и BC параллельны верхнему и нижнему
основаниям цилиндра (рис. 7).

Так как равные сферы с центрами A и P касаются,
то серединой отрезка AP является точка касания этих сфер, при этом AP
= 2R = 6. Аналогично, BP = AB = AC = PC =
BC = 6. Это означает: а) что треугольная пирамида PABC является
правильным тетраэдром с ребром, равным 6; б) скрещивающиеся ребра AP и
BC этого тетраэдра параллельны основаниям цилиндра.

Известно, что в правильном тетраэдре с ребром a
расстояние между скрещивающимися ребрами равно длине их общего серединного
перпендикуляра, то есть равно
В нашем случае, если точка H — середина
AP, точка K — середина BC, то отрезок HK — общий
серединный перпендикуляр ребер AP и BC, при этом

Так как скрещивающиеся ребра AP и BC тетраэдра
параллельны основаниям цилиндра, то HK перпендикулярен основаниям
цилиндра. Учитывая, что прямые AP и BC, содержащие центры шаров,
удалены от параллельных им соответственно верхнего и нижнего оснований цилиндра
на расстояния, равные 3, приходим к выводу: высота h цилиндра равна

Так как скрещивающиеся ребра правильного тетраэдра взаимно
перпендикулярны, то их серединный перпендикуляр HK — ось симметрии
тетраэдра PABC, совпадающая с осью O₁O цилиндра.
Поэтому ребра AP и BC расположены на перпендикулярных диаметрах
EF и MT цилиндра, где E, F, M и T — точки
касания боковой поверхности цилиндра со сферами, центры которых — соответственно
вершины A и P, B и C. Тогда BM = CT =
R,
значит,

MT = BC + 2MB = 4R = 4∙3
= 12 = 2r,

откуда r = 6, где r — радиус основания
цилиндра.

Следовательно, объем цилиндра равен

Ответ:   куб. ед.

Задача 7. Одна из образующих цилиндра расположена на
диаметре шара, а две другие являются хордами этого шара. Найдите радиус
основания и высоту цилиндра, если расстояние между каждой из пар этих образующих
равно 6, а радиус шара равен 10. Определите, весь ли цилиндр находится внутри
шара?

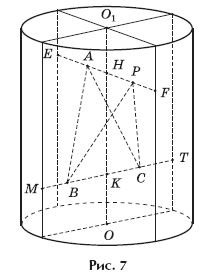
Решение. На рисунке 8 изображено сечение шара (круг ω) и цилиндра (круг ω₁)
плоскостью, проходящей через центр O шара перпендикулярно образующим
цилиндра (эта плоскость делит все образующие цилиндра пополам), при этом точка
O — середина образующей цилиндра, расположенной на диаметре шара, а точки
A и B — середины образующих цилиндра, являющихся данными хордами
шара.

Расстояние между образующими каждой из этих пар равно 6,
поэтому равносторонний треугольник OAB со стороной 6 вписан в круг
ω₁ с центром O₁,
равный основанию цилиндра и имеющий радиус А так как радиус шара равен 10, то
круг ω₁
лежит внутри круга ω с
центром O — диаметрального сечения шара. Это означает, что прямая,
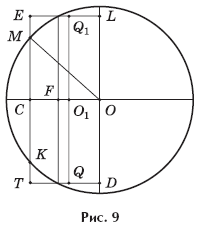
содержащая образующую цилиндра, проходящую через точку C, диаметрально
противоположную точке O (рис. 9), пересекает поверхность шара в некоторых
точках M и K, симметричных относительно диаметральной плоскости
OAB.

Пусть точка A — середина образующей PH
цилиндра, являющейся данной хордой шара.

Тогда OP = OH = 10 (как радиусы шара), и в
прямоугольном треугольнике OAP находим

значит, длина образующей цилиндра равна:

PH = 2AP = 16.

Найдем длину хорды MK шара, которая лежит на
образующей ET цилиндра, содержащей точку C и удаленной от центра
шара на расстояние Для этого рассмотрим сечение данной комбинации тел
диаметральной плоскостью шара, проходящей через ось Q₁Q цилиндра. На рисунке 9 изображены: сечение шара — круг с центром O и
радиусом OM = 10; сечение цилиндра — прямоугольник ELDT.

В прямоугольном треугольнике OCM находим:

поэтому Так как 16² > 1613,
то PH > MK. Значит, образующая ET цилиндра больше хорды
MK шара, которая лежит на этой образующей. Это говорит о том, что концы E
и T образующей ET цилиндра, а значит и некоторые две его части,
симметричные относительно проведенной диаметральной плоскости AOB,
находятся вне шара.

Ответ: нет, часть цилиндра расположена вне шара.

При решении задач на комбинации касающихся фигур вращения
учащимся полезно повторить, что если даны две касающиеся внешним образом
окружности ω(A;
R) и ω₁(B;
r), а прямая m является их общей внешней касательной, то
расстояние HK между точками касания H и K этой прямой с
окружностями ω и
ω₁ равно

Кроме того, учащимся необходимо объяснить, что в некоторых
случаях решению задачи на комбинацию касающихся фигур вращения способствует
«взгляд с различных сторон» на данную комбинацию.

Рассмотрим, например, следующую задачу.

Задача 8. На плоскости лежат цилиндр радиуса R и
два шара радиуса r (R > r). Цилиндр касается плоскости по
своей образующей; шары касаются друг друга и боковой поверхности цилиндра.
Найдите радиус шара, большего, чем данные, касающегося обоих данных шаров,
боковой поверхности цилиндра и плоскости.

Решение. Обозначим: α  —
плоскость, которой касаются все данные в условии задачи тела. Пусть x (x
> r) — искомая длина радиуса шара, касающегося обоих данных шаров,
боковой поверхности цилиндра и плоскости α .

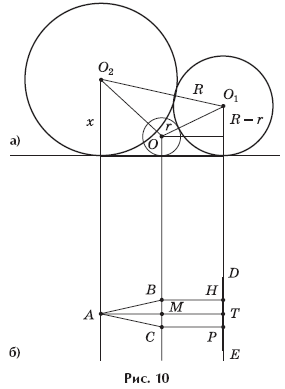
На рисунке 10,б (вид сверху): B и C —
точки, в которых шары радиуса r касаются плоскости
α , BC = 2r;
DE — образующая, по которой цилиндр касается плоскости α; A — точка касания
шара радиуса x и плоскости α .

На рисунке 10,а изображены данные шары и цилиндр в
плоскости, перпендикулярной оси цилиндра (вид — вдоль оси цилиндра). Точки O
и O₁ — центры соответственно шаров радиуса r и
основания цилиндра, точка O₂ — центр шара радиуса x.

Плоскость β,
проведенная через центры O и O₂ шаров с радиусами r
и x перпендикулярно плоскости α,
пересекает эти шары по касающимся кругам, а плоскость
α — по прямой AB,
которая является общей касательной кругов-сечений. Тогда Аналогично,

В сечение шара радиуса x и цилиндра диаметральной
плоскостью этого шара, перпендикулярной оси цилиндра, получаются два касающихся
круга, для которых AT — их общая касательная. Тогда Аналогично,

Далее, в прямоугольном треугольнике ABM ( AMB
= 90°) по теореме
Пифагора имеем:
AB² = AM² + BM².
Находим:

Тогда получаем:

Пусть Решаем уравнение

Получили:

Проверкой убеждаемся, что условию

удовлетворяет лишь

Тогда искомый радиус большего шара равен

Ответ:

Три сферы и более

Прежде чем приступить к решению задач на две, три и более
сферы, целесообразно решить несколько задач на две, три и более окружности. При
этом учащимся полезно знать, что если прямая в точках A и B
касается двух внешним образом касающихся окружностей радиусов R₁
и R₂, то длина отрезка AB равна Кроме того, с учащимися
следует повторить:

Множество всех точек пространства, равноудаленных от двух
равных касающихся сфер (шаров), есть плоскость, проходящая через точку касания
этих сфер (шаров) перпендикулярно линии их центров.

При решении задачи, в которой даны две, три и более попарно
касающиеся сферы, бывает удобно воспользоваться сечением этих сфер плоскостью,
проходящей через их центры (диаметральной плоскостью). Тогда данная задача
сводится к планиметрической задаче на взаимное расположение двух, трех и более
попарно касающихся окружностей.

Иногда бывает удобно «привлечь на помощь» треугольник или
тетраэдр с вершинами в центрах соответственно трех или четырех касающихся данных
сфер; при этом стороны треугольника и ребра тетраэдра равны суммам радиусов
данных сфер.

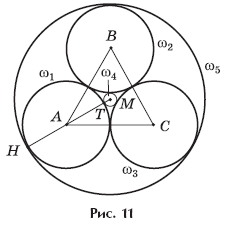
Задача 9.  Три равные сферы радиуса 6 касаются друг друга.
Найдите радиус сферы, касающейся всех этих сфер, если ее центр лежит в плоскости
центров трех данных сфер.

Решение. Обозначим: точки A, B, C —
центры трех данных касающихся друг друга сфер радиуса 6; точка K —
центр касающейся сферы.

Рассмотрим сечение данной комбинации сфер плоскостью ABC,
проведенной через их центры, при этом K
(ABC).

В сечении получаем три равные попарно касающиеся окружности
ω₁,
ω₂,
ω₃ с центрами A,
B и C радиуса 6 (рис. 11).
Тогда треугольник ABC —
равносторонний; AB = 12;

где M — центроид треугольника ABC.

Окружность ω₄
с центром K — сечение сферы, касающейся трех данных сфер, — касается
окружностей ω₁,
ω₂,
ω₃. Так как, с
одной стороны, (в треугольнике ABC) и, с другой стороны, центр K
окружности ω₄,
касающейся равных окружностей ω₁,
ω₂,
ω₃, равноудален от
их центров A, B и C, то центр K окружности
ω₄ совпадает с
центроидом M треугольника ABC.

Обозначим через T и H точки пересечения прямой
MA с окружностью ω₁.

Тогда отрезки MT и MH равны радиусам концентрических окружностей
ω₄ и
ω₅ с центром M,
одна из которых касается окружностей ω₁,
ω₂,
ω₃ внутренним
образом, друга — внешним. Так как

MT = AM – AT, MH = AM + AH,

то

Таким образом, существуют две концентрические сферы с центром
M, касающиеся всех данных трех сфер: радиус одной сферы равен , а радиус другой —

Ответ: ; .

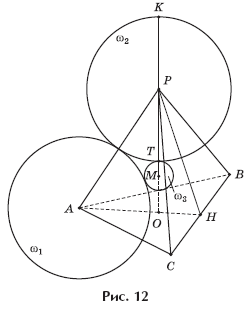
Задача 10.  В вершинах правильного тетраэдра с ребром 18
расположены центры четырех равных сфер, попарно касающихся друг друга. Найдите
радиус сферы, касающейся всех этих сфер.

Решение. Пусть центрами данных сфер являются вершины
правильного тетраэдра PABC, а центром сферы, касающейся всех этих сфер,
служит некоторая точка F.

Известно, что точка касания двух сфер принадлежит линии их
центров и расстояние между центрами данных сфер равно сумме длин их радиусов
(сферы касаются внешним образом). Это означает: FA = FB = FC
= FP (данные четыре сферы равны), то есть точка F равноудалена от
вершин данного правильного тетраэдра.

Известно, что в правильном тетраэдре PABC точкой,
равноудаленной от всех его вершин, является точка M пересечения отрезов,
соединяющих вершины тетраэдра с центроидами противоположных граней, причем где
O — центроид правильного треугольника ABC. Таким образом, центром
сферы, касающейся всех четырех данных сфер, является точка M.

На рисунке 12 изображено сечение данной комбинации тел
плоскостью APH (H — середина BC), где (APH)
BC, (APH)
(ABC),
так как высота тетраэдра PO расположена в плоскости APH. Сечением
тетраэдра этой плоскостью является треугольник APH, а сечением двух
данных сфер с центрами A и P — две равные касающиеся окружности
ω₁ и
ω₂ с теми же
центрами и радиусом 6. Так как центр M сферы, касающейся всех четырех
данных сфер, принадлежит секущей плоскости APH, то ее сечением является
окружность ω₃,
касающаяся окружностей ω₁
и ω₂, а
радиус окружности ω₃
равен радиусу этой сферы. Найдем радиус окружности
ω₃.

В правильном треугольнике ABC со стороной 18 имеем:

Тогда в прямоугольном треугольнике AOP (OP AO):

Теперь находим:

Обозначим через T и K  точки пересечения
прямой MP с окружностью ω₂.
Тогда отрезки MT и MK равны радиусам концентрических окружностей
ω₃ и
ω₄ с центром M,
одна из которых касается окружностей ω₁
и ω₂
внутренним образом, другая — внешним. Так как

MT = PM – PT, MK = PM + PK,

то

Таким образом, существуют две концентрические окружности с
центром M, касающиеся всех данных четырех сфер: радиус одной сферы равен
, а радиус другой — .

Ответ: ; .

Аналогичные задачи можно найти в задачнике для 11-го класса упомянутого выше
УМК. Среди них задачи 3.339–3.354, 3.355–3.375, 3.379–3.384, 3.397–3.403,
3.429–3.434, 3.436–3.444, 3.467–3.474, 3.477.

Потоскуев Е.

В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.

Нахождение радиуса сферы/шара

Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.

Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.

Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие (l) – его боковые стороны (AB и BC).

Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:

1. Через образующую и радиус основания конуса:

2. Через высоту и радиус основания конуса

Высота (h) конуса – это отрезок BE на рисунках выше.

Формулы площади и объема сферы/шара

Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:

Примечание: π округленно равняется 3,14.

Автор	Сообщение
	Заголовок сообщения: Вписанный в сферу усеченный конус Добавлено: 20 ноя 2011, 19:17
Оракул Зарегистрирован: 22 мар 2011, 20:12 Сообщений: 898 Откуда: Сочи Cпасибо сказано: 484 Спасибо получено: 248 раз в 189 сообщениях Очков репутации: 105	В сферу вписан усеченный конус, радиусы оснований которого равны 15 см и 24 см, высота равна 27 см. Нужно найти радиус сферы. Там получится окружность, описанная около трапеции. Но как найти этот радиус? Мы не знаем, где вообще будет центр окружности. Если рассматривать два случая, но каких и как? Подскажите
Вернуться к началу

Sviatoslav	Заголовок сообщения: Re: Вписанный в сферу усеченный конус Добавлено: 20 ноя 2011, 20:29
	И у них ответ красивый, 25, а у меня чушь какая-то получается Получается система (значка системы так и не нашел) [math]x + y = EG[/math] [math]{y^2} + G{C^2} = {x^2} + E{B^2}[/math] [math]x + y = 27[/math] [math]{y^2} + 144 = {x^2} + 56.25[/math] [math]y = 11.875[/math] Ну и там ужас. Может, ошибка в ответе или условии?
Вернуться к началу