В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.
Примечание: Напомним, что в любой куб можно вписать шар.
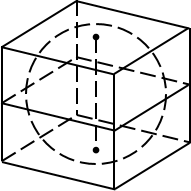
Для начала выполним чертеж.
- шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
- центр шара – точка O, которая также является центром куба.
Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:
R = a/2, где “a” – ребро куба (является стороной его грани).
Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.
Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.
Радиус вписанного шара через диагональ куба
Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:
Радиус вписанной сферы куба представляет собой половину ребра куба, так как диаметр такой сферы точно совпадает с самим ребром. Поэтому чтобы найти ребро куба через радиус вписанной сферы, нужно умножить последний на два. (рис.2.2)
a=2r
Найти площадь стороны куба можно как площадь квадрата, стороной которого является ребро куба. Тогда, вместо того чтобы возводить во вторую степень ребро, нужно возвести удвоенный радиус вписанной в куб сферы. Площадь боковой поверхности куба и площадь полной поверхности куба будут равны четырем и шести таким площадям соответственно, так как они представлены эти количеством граней куба.
S=a^2=4r^2
S_(б.п.)=4S=16r^2
S_(п.п.)=6S=24r^2
Чтобы вычислить объем, необходимо возвести в куб ребро a или удвоенный радиус вписанной сферы. Таким образом, мы получим, что объем куба через радиус сферы, вписанной в него, равен кубу этого радиуса, умноженному на 8.
V=a^3=8r^3
Периметр куба, как сумма длин всех ребер по одной стороне, равен произведению длины одного ребра и двенадцать. Периметр, выраженный через радиус вписанной окружности, равен 24 таким радиусам.
P=12a=24r
Диагональ стороны куба, то есть диагональ квадрата, вычисляется как произведение ребра куба на корень из двух, в данном случае она будет выглядеть как произведение радиуса вписанной сферы на 2 корня из двух.
d=a√2=2√2 r
Чтобы найти диагональ куба через радиус вписанной сферы, воспользуемся готовой формулой для диагонали куба через ребро и подставим вместо него удвоенный радиус. (рис.2.1.)
D=a√3=2√3 r
Радиус окружности, описанной вокруг куба, равен половине диагонали, как видно из рисунка. Так как диагональ куба равна удвоенному произведению радиуса и корня из трех, то разделив это выражение на два, коэффициенты сократятся, и останется только радиус, умноженный на корень из трех. (рис.2.3.)
R=D/2=(2√3 r)/2=√3 r
Найдите радиус окружности вписанной в куб
Радиус вписанной сферы куба
Свойства
Радиус вписанной сферы куба представляет собой половину ребра куба, так как диаметр такой сферы точно совпадает с самим ребром. Поэтому чтобы найти ребро куба через радиус вписанной сферы, нужно умножить последний на два. (рис.2.2) a=2r
Найти площадь стороны куба можно как площадь квадрата, стороной которого является ребро куба. Тогда, вместо того чтобы возводить во вторую степень ребро, нужно возвести удвоенный радиус вписанной в куб сферы. Площадь боковой поверхности куба и площадь полной поверхности куба будут равны четырем и шести таким площадям соответственно, так как они представлены эти количеством граней куба. S=a^2=4r^2 S_(б.п.)=4S=16r^2 S_(п.п.)=6S=24r^2
Чтобы вычислить объем, необходимо возвести в куб ребро a или удвоенный радиус вписанной сферы. Таким образом, мы получим, что объем куба через радиус сферы, вписанной в него, равен кубу этого радиуса, умноженному на 8. V=a^3=8r^3
Периметр куба, как сумма длин всех ребер по одной стороне, равен произведению длины одного ребра и двенадцать. Периметр, выраженный через радиус вписанной окружности, равен 24 таким радиусам. P=12a=24r
Диагональ стороны куба, то есть диагональ квадрата, вычисляется как произведение ребра куба на корень из двух, в данном случае она будет выглядеть как произведение радиуса вписанной сферы на 2 корня из двух. d=a√2=2√2 r
Чтобы найти диагональ куба через радиус вписанной сферы, воспользуемся готовой формулой для диагонали куба через ребро и подставим вместо него удвоенный радиус. (рис.2.1.) D=a√3=2√3 r
Радиус окружности, описанной вокруг куба, равен половине диагонали, как видно из рисунка. Так как диагональ куба равна удвоенному произведению радиуса и корня из трех, то разделив это выражение на два, коэффициенты сократятся, и останется только радиус, умноженный на корень из трех. (рис.2.3.) R=D/2=(2√3 r)/2=√3 r
Нахождение радиуса вписанного в куб шара
В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.
Примечание: Напомним, что в любой куб можно вписать шар.
Для начала выполним чертеж.
- шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
- центр шара – точка O, которая также является центром куба.
Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:
R = a/2, где “a” – ребро куба (является стороной его грани).
Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.
Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.
Радиус вписанного шара через диагональ куба
Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:
Найдите радиус сферы, вписанный в куб, диагональ которого равна 2корня из 3?
Геометрия | 10 — 11 классы
Найдите радиус сферы, вписанный в куб, диагональ которого равна 2корня из 3.
Диаметр сферы, вписанной в куб, равен стороне куба.
(Диаметр соединяет середины противоположных граней куба.
Расстояние между ними равно стороне куба).
Значит, радиус сферы равен половине стороны куба.
Диагональ куба в√3 раз больше его стороны.
Значит, если диагональ равна 2√3, то сторона равна 2.
Таким образом, радиус сферы равен 1.
1. Ребро правильного тетраэдра равно 4 см?
1. Ребро правильного тетраэдра равно 4 см.
Найдите радиус сферы, вписанной в тетраэдр.
2. Найдите ребро правильного тетраэдра, вписанного в сферу радиуса R.
Найдите радиус шара, вписанного в куб, если ребро куба равно 8?
Найдите радиус шара, вписанного в куб, если ребро куба равно 8.
Диагональ квадрата равна 6 корней из 2 чему равен радиус вписанной окружности?
Диагональ квадрата равна 6 корней из 2 чему равен радиус вписанной окружности.
Диагональ грани куба равна 3 корня из 2?
Диагональ грани куба равна 3 корня из 2.
Найдите объем куба.
Ребро куба равно а?
Ребро куба равно а.
Найдите радиус шара : а) вписанного в кууб б) описанного около куба.
В куб вписана сфера, r = 5?
В куб вписана сфера, r = 5.
Найдите Sповерхности куба.
В куб, диагональ грани которого равна 4, вписан шар?
В куб, диагональ грани которого равна 4, вписан шар.
Найти квадрат радиуса шара.
В куб со стороной A вписана сфера ?
В куб со стороной A вписана сфера .
Найдите объём части куба находяшейся вне сферы.
В квадрат вписана окружность Найти радиус окружности если диагональ равна 12 корней из 2?
В квадрат вписана окружность Найти радиус окружности если диагональ равна 12 корней из 2.
В сферу радиуса R вписана правильная четырёхугольная призма, у которой диагональ наклонена к плоскости основания под углом а?
В сферу радиуса R вписана правильная четырёхугольная призма, у которой диагональ наклонена к плоскости основания под углом а.
Найдите боковую поверхность призмы.
На этой странице находится вопрос Найдите радиус сферы, вписанный в куб, диагональ которого равна 2корня из 3?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
Радиус вписанной сферы куба
Свойства
Радиус вписанной сферы куба представляет собой половину ребра куба, так как диаметр такой сферы точно совпадает с самим ребром. Поэтому чтобы найти ребро куба через радиус вписанной сферы, нужно умножить последний на два. (рис.2.2) a=2r
Найти площадь стороны куба можно как площадь квадрата, стороной которого является ребро куба. Тогда, вместо того чтобы возводить во вторую степень ребро, нужно возвести удвоенный радиус вписанной в куб сферы. Площадь боковой поверхности куба и площадь полной поверхности куба будут равны четырем и шести таким площадям соответственно, так как они представлены эти количеством граней куба. S=a^2=4r^2 S_(б.п.)=4S=16r^2 S_(п.п.)=6S=24r^2
Чтобы вычислить объем, необходимо возвести в куб ребро a или удвоенный радиус вписанной сферы. Таким образом, мы получим, что объем куба через радиус сферы, вписанной в него, равен кубу этого радиуса, умноженному на 8. V=a^3=8r^3
Периметр куба, как сумма длин всех ребер по одной стороне, равен произведению длины одного ребра и двенадцать. Периметр, выраженный через радиус вписанной окружности, равен 24 таким радиусам. P=12a=24r
Диагональ стороны куба, то есть диагональ квадрата, вычисляется как произведение ребра куба на корень из двух, в данном случае она будет выглядеть как произведение радиуса вписанной сферы на 2 корня из двух. d=a√2=2√2 r
Чтобы найти диагональ куба через радиус вписанной сферы, воспользуемся готовой формулой для диагонали куба через ребро и подставим вместо него удвоенный радиус. (рис.2.1.) D=a√3=2√3 r
Радиус окружности, описанной вокруг куба, равен половине диагонали, как видно из рисунка. Так как диагональ куба равна удвоенному произведению радиуса и корня из трех, то разделив это выражение на два, коэффициенты сократятся, и останется только радиус, умноженный на корень из трех. (рис.2.3.) R=D/2=(2√3 r)/2=√3 r
Нахождение радиуса вписанного в куб шара
В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.
Примечание: Напомним, что в любой куб можно вписать шар.
Для начала выполним чертеж.
- шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
- центр шара – точка O, которая также является центром куба.
Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:
R = a/2, где “a” – ребро куба (является стороной его грани).
Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.
Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.
Радиус вписанного шара через диагональ куба
Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:
[spoiler title=”источники:”]
http://geleot.ru/education/math/geometry/calc/cube/radius_of_inscribed_sphere
[/spoiler]
Перед тем, как смело броситься на амбразуру решения задачи по нахождению радиуса сферы, нужно узнать, что вообще такое сфера и шар. Стереометрия говорит нам, что сфера – это поверхность, состоящая из массы точек пространства, которые находятся на одном расстоянии от центра. Эта точка – центр сферы, а радиус сферы (R) – это расстояние, на которое каждая точка удалена от центра сферы. Шар – это тело, которое ограничено поверхностью сферы.
Безусловно, способ определения того самого радиуса сферы будет зависеть от данных, которые у нас есть.
Способ 1. Определение радиуса сферы при помощи площади ее поверхности
Допустим, нам дана сфера вместе с площадью её поверхности. В таком случае мы будем использовать формулу площади её поверхности для того, чтобы вычислить радиус.
где S – это площадь поверхности сферы, число Пи = 3,14.
Способ 2. Определение радиуса сферы при помощи объема шара
Если нам дан объём шара, ограниченного сферой, то радиус находится так:
где V – это объём шара, число Пи = 3,14.
Способ 3. Альтернативные формулы определения радиуса сферы
В случае, если наша сфера вписана в правильный многогранник или описана вокруг него, можно воспользоваться следующим рядом формул.
Формула 1. Сфера вписана в правильный тетраэдр
Для сферы, которая вписана в правильный тетраэдр:
где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).
Формула 2. Сфера описана около правильного тетраэдра
Для сферы, которая описана около правильного тетраэдра:
где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).
Формула 3. Сфера вписана в куб
Для сферы, которая вписана в куб:
где a – длина ребра куба.
Формула 4. Сфера описана около куба
Для сферы, которая описана около куба:
где a – длина ребра куба.
22 января 2014
Это реальная задача из ЕГЭ по математике. Решается устно, если знать алгоритм. Тем не менее, мы подробно разберем все ключевые моменты решения этой задачи.
Задача B13. Найдите радиус сферы, вписанной в куб, ребра которого равны 42.

Самое веселое состоит в том, что искомый радиус уже присутствует на рисунке, т.е. для решения нужна обычная наблюдательность и хотя бы чуть-чуть трехмерного мышления. Тем не менее, «взгляд со стороны» на эту сферу дает нам больше уверенности в том, что мы ищем именно тот отрезок, который приведет нас к правильному ответу — радиусу.
Смотрите также:
- Сфера, описанная вокруг куба
- Случай четырехугольной пирамиды
- Сложение и вычитание дробей
- Комментарий к пробному ЕГЭ от 7 декабря
- Формулы приведения: ускоряем вычисления в тригонометрии
- Задача C1: показательные уравнения с ограничением