В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.
- Нахождение радиуса сферы/шара
- Формулы площади и объема сферы/шара
Нахождение радиуса сферы/шара
Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.

Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.

Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие (l) – его боковые стороны (AB и BC).
Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:
1. Через образующую и радиус основания конуса:

2. Через высоту и радиус основания конуса
![]()
Высота (h) конуса – это отрезок BE на рисунках выше.
Формулы площади и объема сферы/шара
Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:
![]()

Примечание: π округленно равняется 3,14.
Введение
Как всегда, речь пойдет исключительно о прямых круговых конусах и усеченных конусах (см. Рис. 1).

Рис.1 Прямой круговой и усеченный
Шар, описанный около конуса
Шар называют описанным около конуса, если вершина конуса и окружность основания конуса принадлежат поверхности шара. Конус в этом случае называют вписанным в шар (см. Рис. 2). Аналогично с усеченным: его можно вписать в шар, если окружности обоих его оснований лежат на поверхн

Рис.2 Шар, описанный около конуса
Всегда ли конус можно вписать в шар? Оказывается, что всегда.
Доказательство. Пусть ![]() – вершина конуса,
– вершина конуса, ![]() – диаметр его основания,
– диаметр его основания, ![]() – высота конуса (
– высота конуса (![]() ).
).

Рис.3 Иллюстрация условия
Тогда рассмотрим осевое сечение ![]() , около которого можно описать окружность (свойство треугольника) (см. Рис. 4).
, около которого можно описать окружность (свойство треугольника) (см. Рис. 4).

Рис.4 Окружность, описанная около треугольника ![]()
Отметим точку ![]() – центр описанной окружности около треугольника
– центр описанной окружности около треугольника ![]() . Она лежит на перпендикуляре
. Она лежит на перпендикуляре ![]() , но не обязательно строго на отрезке
, но не обязательно строго на отрезке ![]() – она может лежать и вне его, вне конуса, например под точкой
– она может лежать и вне его, вне конуса, например под точкой ![]() (см. Рис.5).
(см. Рис.5).

Рис.5 Возможные расположения точки ![]()
Но это неважно. Важно доказать, что если точка ![]() равноудалена от точек
равноудалена от точек ![]() ,
, ![]() и
и ![]() (см. Рис. 6), то она является центром описанного шара.
(см. Рис. 6), то она является центром описанного шара.

Рис.6 ![]() равноотдалена от точек
равноотдалена от точек ![]() ,
, ![]() и
и ![]()
Для этого необходимо доказать, что точка ![]() и все точки основания лежат на поверхности шара. Рассмотрим шар с центром в точке
и все точки основания лежат на поверхности шара. Рассмотрим шар с центром в точке ![]() и радиусом
и радиусом ![]() (см. Рис. 7).
(см. Рис. 7).

Рис. 7 Шар с центром в точке ![]() и радиусом
и радиусом ![]()
По построению ![]() , значит, точки
, значит, точки ![]() и
и ![]() также лежат на поверхности шара (они удалены на радиус
также лежат на поверхности шара (они удалены на радиус ![]() ). С другой стороны, если рассмотреть любую точку
). С другой стороны, если рассмотреть любую точку ![]() , которая лежит на основании конуса, то
, которая лежит на основании конуса, то ![]() (по двум катетам:
(по двум катетам: ![]() – общий катет,
– общий катет, ![]() – как радиусы основания) (см. Рис. 8).
– как радиусы основания) (см. Рис. 8).

Рис.8 ![]()
Тогда гипотенузы тоже равны ![]() , значит,
, значит, ![]() , откуда следует, что точка
, откуда следует, что точка ![]() также лежит на поверхности шара.
также лежит на поверхности шара.
Либо проще. ![]() – перпендикуляр, ось конуса. Любая точка на оси равноудалена от точек окружности основания. Тогда, раз точка
– перпендикуляр, ось конуса. Любая точка на оси равноудалена от точек окружности основания. Тогда, раз точка ![]() равноудалена от точек
равноудалена от точек ![]() ,
, ![]() и
и ![]() , значит, она и является центром искомого шара (см. Рис. 9). Что и требовалось доказать.
, значит, она и является центром искомого шара (см. Рис. 9). Что и требовалось доказать.

Рис. 9 ![]() – центр искомого шара
– центр искомого шара
Доказательство.
Докажем, что конус всегда можно вписать в шар. По сути, нужно найти точку, которая равноудалена от вершины конуса и всех вершин окружности его основания. Заметим, что ГМТ (ГМТ – геометрическое место точек) равноудаленных от окружности основания, – это перпендикуляр, проведенный к плоскости основания из центра этой окружности (см. Рис. 1).

Рис.1 ГМТ, равноудаленных от окружности основания
С другой стороны, ГМТ равноудаленных от точек ![]() и
и ![]() – это плоскость, проходящая через середину отрезка
– это плоскость, проходящая через середину отрезка ![]() , перпендикулярная ему. Очевидно, эта плоскость не параллельна высоте конуса, а значит, пересекает ее (см. Рис. 2).
, перпендикулярная ему. Очевидно, эта плоскость не параллельна высоте конуса, а значит, пересекает ее (см. Рис. 2).

Рис.2 ГМТ равноудаленных от точек ![]() и
и ![]()
Точка пересечения и будет искомым центром шара, т. к. она равноудалена от точек основания конуса и от его вершины (см. Рис. 3). Отметим, что эта точка может быть как внутри конуса, так и вне его.

Рис.3 Точка пересечения плоскости и высоты конуса
Пример 1
Дан конус, образующая ![]() , высота
, высота ![]() . Найти радиус описанного шара
. Найти радиус описанного шара ![]() .(см. Рис. 10).
.(см. Рис. 10).

Рис.10 Иллюстрация к примеру
Решение. Как известно, центр шара совпадает с центром окружности, описанной около треугольника, являющимся осевым сечением конуса. Соответственно, радиус описанного шара равен радиусу этой окружности. Тогда найдем радиус окружности, описанной около треугольника ![]() . Рассмотрим осевое сечение
. Рассмотрим осевое сечение ![]() (см. Рис. 11).
(см. Рис. 11).

Рис. 11 Осевое сечение ![]()
Видно, что ![]() и
и ![]() – египетские, значит,
– египетские, значит, ![]() . (см. Рис. 12).
. (см. Рис. 12).

Рис. 12 Египетские треугольники в осевом сечении
По следствию из теоремы синусов ![]() (см. Рис. 13).
(см. Рис. 13).
 |
Рис.13 Иллюстрация к теореме синусов

Ответ: ![]() .
.
Можно было найти радиус и по формуле ![]() .
.
Шар, описанный около усеченного конуса
Шар называют описанным около усеченного конуса, если оба основания усеченного конуса лежат на поверхности шара (см. Рис. 14).

Рис.14 Шар, описанный около усеченного конуса
Всегда ли усеченный конус можно вписать в шар? Рассмотрим осевое сечение, на этот раз им будет трапеция (см. Рис. 15).

Рис. 15 Трапеция – осевое сечение
Нужно, чтобы около осевого сечения можно было описать окружность (см. Рис. 16).

Рис. 16 Вписанная в окружность трапеция
Это можно сделать только в том случае, когда трапеция равнобедренная. С другой стороны, образующие всегда равны, значит, трапеция будет равнобедренной. То есть около любого усеченного конуса можно описать шар, и центр этого шара будет совпадать с центром окружности, описанной около осевого сечения. Аналогично с радиусом – радиус шара мы будем искать как радиус описанной около трапеции окружности (см. Рис. 17).

Рис. 17 Центр и радиус описанного шара
Рассмотрим теорию на примере.
Пример 2
Дан усеченный конус, радиусы оснований ![]() ,
, ![]() , а высота
, а высота ![]() . Найти радиус шара, описанного около данного усеченного конуса
. Найти радиус шара, описанного около данного усеченного конуса ![]() (см. Рис. 18).
(см. Рис. 18).

Рис.18 Иллюстрация к примеру
Решение. Необходимо найти радиус окружности, описанной около трапеции ![]() . Рассмотрим осевое сечение – равнобедренную трапецию
. Рассмотрим осевое сечение – равнобедренную трапецию ![]() (
(![]() как образующие). Ее основания
как образующие). Ее основания ![]() ,
, ![]() (диаметры оснований усеченного конуса), высота
(диаметры оснований усеченного конуса), высота ![]() (см. Рис. 19).
(см. Рис. 19).

Рис. 19 Выносной рисунок трапеции
Найдем радиус описанной окружности двумя способами.
Способ 1. Пусть ![]() – центр искомой описанной окружности. Опустим перпендикуляр
– центр искомой описанной окружности. Опустим перпендикуляр ![]() – он разделит отрезки
– он разделит отрезки ![]() и
и ![]() пополам. Пусть
пополам. Пусть ![]() ,
, ![]() и
и ![]() (как радиусы описанной окружности) (см. Рис. 20).
(как радиусы описанной окружности) (см. Рис. 20).

Рис.20 Способ 1
Рассмотрим ![]() и
и ![]() . По теореме Пифагора:
. По теореме Пифагора:
![]()
Раскрывая скобки и вычитая из верхнего нижнее, находим ![]() .
.
![]()
![]()
![]()
![]()
Получили, что длина отрезка отрицательная. На самом деле, противоречия нет, просто мы неверно отметили точку ![]() . То, что
. То, что ![]() отрицателен, означает, что на самом деле точка
отрицателен, означает, что на самом деле точка ![]() лежит ниже
лежит ниже ![]() . В этом случае
. В этом случае ![]() , а не
, а не ![]() (см. Рис. 21).
(см. Рис. 21).

Рис. 21 Верное положение точки ![]()
Тогда получаем, что ![]() ;
; ![]() .
.

Способ 2. Можно найти радиус описанной окружности как радиус окружности, описанной около треугольника, вершины которого являются также вершинами трапеции, например ![]() (см. Рис. 22).
(см. Рис. 22).

Рис.22 Радиус искомой окружности совпадает с радиусом окружности, описанной около треугольника
Найдем радиус по формуле ![]() .
.
Проведем ![]() и
и ![]() – высоты трапеции.
– высоты трапеции.
![]()
Далее, ![]() .
.
Тогда ![]() ,
, ![]() (см. Рис. 23).
(см. Рис. 23).

Рис.23 Вычисление элементов ![]()
Значит ![]() .
.
Ответ:![]() .
.
Шар, вписанный в конус (усеченный конус)
Шар вписан в конус, если поверхность шара касается основания конуса и его боковой поверхности (см. Рис. 24).

Рис.24 Шар, вписанный в конус
Что значит «шар касается основания и боковой поверхности»? Касание шара с основанием – это касание шара плоскости основания (см. Рис. 25).

Рис.25 Касание шара с плоскостью основания
Под фразой «шар касается боковой поверхности конуса» подразумевается, что шар «не выходит» за границы конуса, однако соприкасается с ним, то есть у них есть общая окружность на боковой поверхности (см. Рис. 26).

Рис.26 Общая окружность при касании шара с боковой поверхностью
Радиус такого шара ищется через радиус окружности, вписанной в осевое сечение (см. Рис. 27).

Рис.27 Окружность, вписанная в осевое сечение
Возникает вопрос: всегда ли шар можно вписать в конус? Всегда, т. к. в треугольник всегда можно вписать окружность.
Шар вписан в усеченный конус, если он касается оснований усеченного конуса и его боковой поверхности (см. Рис. 28).

Рис.28 Шар, вписанный в усеченный конус


Радиус такого шара можно найти через радиус окружности, вписанной в осевое сечение – трапецию (см. Рис. 29).
Шар вписать в усеченный конус можно не всегда, ведь в трапецию можно вписать окружность тогда и только тогда, когда сумма оснований равна сумме боковых сторон (см. Рис. 30).
Рис.30 Суммы противоположных сторон
Иначе говоря, сумма радиусов усеченного конуса должна быть равна образующей (см. Рис. 31) – это необходимое и достаточное условие для существования вписанного в усеченный конус шара.
Рис. 31 Сумма радиусов равна
Пример 3
Дан конус, ![]() ,
, ![]() . Найти радиус вписанного в него шара
. Найти радиус вписанного в него шара ![]() (см. Рис. 32).
(см. Рис. 32).

Рис.32 Иллюстрация к задаче
Решение. Достаточно найти радиус окружности, вписанной в треугольник – осевое сечение. Рассмотрим осевое сечение ![]() .
. ![]() (образующие конуса),
(образующие конуса), ![]() ,
, ![]() , тогда
, тогда ![]() . По теореме Пифагора из
. По теореме Пифагора из ![]() (прямоугольный)
(прямоугольный) ![]() Получаем
Получаем ![]() , тогда
, тогда ![]() (см. Рис. 33).
(см. Рис. 33).

Тогда по формуле
![]() .
.
Рис.33 Выносной рисунок осевого сечения

Ответ:
![]() .
.
Рис.34 Иллюстрация к условию задачи
Задача
Дан усеченный конус, в который вписан шар. Основания конуса ![]() и
и ![]() . Найти радиус вписанного шара
. Найти радиус вписанного шара ![]() (см. Рис. 34).
(см. Рис. 34).

Решение. Рассмотрим осевое сечение – это равнобедренная трапеция. Так как в нее можно вписать окружность, то образующая равна сумме радиусов, то есть 15.
Рис.35 Равнобедренная трапеция в сечении

Проведем две высоты. Получаем, что отрезки, на которые они разделили основание, равны 9-6-9 (см. Рис. 36).
Рис.36 Проведенные высоты
Значит, по теореме Пифагора ![]() (см. Рис. 37).
(см. Рис. 37).

Тогда
![]() .
.
Ответ:![]() .
.
Рис. 37. Прямоугольный
Заключение
Сегодня речь шла о таких конструкциях, как шар – конус и шар – усеченный конус. Мы выяснили, когда шар можно описать около конуса и усеченного конуса и как искать радиус такого шара (радиус описанного шара – это радиус окружности, описанной около осевого сечения конуса (усеченного конуса)). Кроме того, мы выяснили, когда шар можно вписать в конус (усеченный конус) и как искать радиус такого шара (радиус вписанного шара – это радиус окружности, вписанной в осевое сечение конуса (усеченного конуса)).
Список литературы
Атанасян Л.С. и др. 18-е изд. Геометрия. Учебник для 10–11 классов. – М.: Просвещение, 2009. – 255 с. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002. Рабочая тетрадь по геометрии 11 класс, В.Ф. Бутузов, Ю.А. Глазков
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-сайт hot.ee (Источник)
- Интернет-сайт hot.ee (Источник)
- Интернет-сайт schools.keldysh.ru (Источник)
Домашнее задание
Равносторонний конус (осевое сечение – равносторонний треугольник) вписан в шар. Найдите радиус шара, если образующая конуса равна 6 см. В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите объем шара, если объем конуса равен 12. Около сферы радиуса ![]() описан конус, высота которого равна
описан конус, высота которого равна ![]() . Найдите площадь полной поверхности конуса.
. Найдите площадь полной поверхности конуса.
Ответ:
8√3 см
Объяснение:
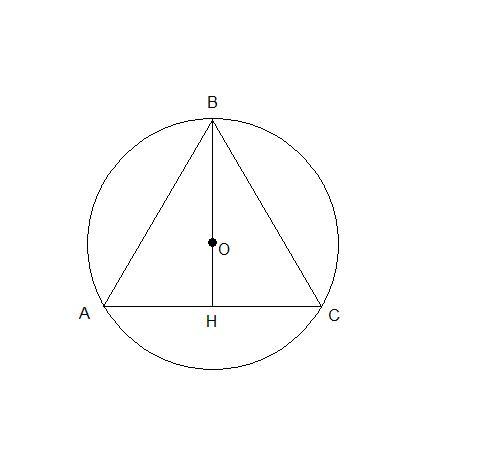
Шар описан вокруг конуса, значит осевое сечение конуса вписано в большой круг шара.
Радиус шара равен радиусу окружности, описанной около равностороннего треугольника со стороной 24 см.
Формула радиуса описанной окружности для правильного треугольника со стороной а:
см
Приложения:
Шар является описанным около куба, если все вершины куба находятся на поверхности шара.


Центр шара (O) — точка пересечения диагоналей куба.
Около любого куба можно описать шар.
Общие точки шара и куба — восемь вершин куба.
Чертится диагональное сечение.
и
CA1
— диагонали куба.
Радиус шара равен половине диагонали куба.
Шар является вписанным в куб, если он касается всех его граней.


Центр шара (O) находится в точке пересечения диагоналей куба.
В любой куб можно вписать шар.
Общие точки шара и куба — центры шести граней куба (точки касания шара и куба).
Чертится сечение плоскостью, которая параллельна грани куба и проходит через центр шара.
Радиус шара — половина стороны куба.
Шар является описанным около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.


Центр шара (O) находится в середине высоты цилиндра.
Общие элементы — две окружности.
Около любого цилиндра можно описать шар.
Чертится осевое сечение.
Радиус шара — половина диагонали осевого сечения цилиндра.
Шар является вписанным в цилиндр, если касается оснований цилиндра и всех его образующих.
Центр шара (O) — середина высоты цилиндра.
Осевое сечение — квадрат с вписанной в него окружностью.
Радиус шара равен радиусу цилиндра и половине высоты цилиндра.
Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Числовые ряды. Необходимый признак сходимости. Признак Даламбера
1 ставка
Где найти ответы на ОГЭ 2023?
1 ставка
Написать экологическое обоснование изделия из кольца
1 ставка
Высшая математика. Помогите пожалуйста, очень нужно!
1 ставка
Не хотят брать в 11 класс
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
тань сергеевна
Знаток
(484),
закрыт
15 лет назад
Лучший ответ
Nau
Просветленный
(23621)
15 лет назад
Ответ:
r=(R^2+H^2)/(2*H)
Все из теоремы Пифагора.
Остальные ответы
Alexey Burdin
Мыслитель
(9287)
15 лет назад
не всё
ещё из подобия треугольников
2r/l=l/H
r=l^2/(2H)=(R^2+H^2)/(2H)
Похожие вопросы
