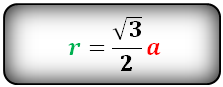Шестиугольник является правильным многоугольником, так как у него все стороны и углы равны. А значит, около любого шестиугольника можно описать окружность.

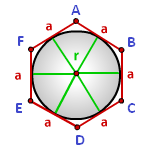
Центр правильного многоугольника равноудален от его вершин. Отрезок, соединяющий центр с вершинами называется радиусом правильного многоугольника и также является радиусом описанной около него окружности.
Формула радиуса описанной окружности около шестиугольника
Существует классическая формула для нахождения радиуса описанной окружности около правильного многоугольника
Для правильного шестиугольника n=6, тогда угол будет равен
По тригонометрической таблице sin(30°)=
Тогда формула радиуса описанной окружности около шестиугольника имеет следующий вид
Радиус описанной окружности около шестиугольника равен его стороне
Пример расчета радиуса окружности описанной около шестиугольника
Найдите радиус окружности описанной около правильного шестиугольника, если радиус вписанной окружности в него равен
Радиус описанной окружности около шестиугольника имеет вид R = a
Применив формулу радиуса вписанной окружности в шестиугольник, получаем:
Выразим сторону шестиугольника:
Выразим радиус описанной окружности через радиус вписанной: 
Радиус окружности, описанной около правильного шестиугольника
Содержание:
- Что такое окружность, описанная около правильного шестиугольника
- Как найти радиус, формула
- Свойства окружности, описанной около шестиугольника
- Площадь круга, ограниченного описанной окружностью
- Пример расчета радиуса окружности, описанной около шестиугольника
Что такое окружность, описанная около правильного шестиугольника
Правильный шестиугольник — выпуклый шестиугольник, у которого все стороны и углы равны.
Описанная около многоугольника окружность — это окружность, которая содержит все вершины выпуклого многоугольника. Ее центром является точка пересечения срединных перпендикуляров к сторонам многоугольника, обычно её обозначают прописной буквой О.
Как найти радиус, формула
Для расчетов используем формулу радиуса окружности, описанной около правильного многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула 1
(R=frac a{2sinleft(frac{360^0}{2n}right)})
где R — радиус описанной окружности правильного многоугольника,
а — длина стороны многоугольника,
n — количество сторон (или вершин) многоугольника.
Подставим в формулу значение n=6.
(R=frac a{2sinleft(frac{360^0}{2n}right)}=R=frac a{2sinleft(frac{360^0}{2·6}right)}=frac a{2sinleft(frac{360^0}{12}right)}=frac a{2sin30^0}.)
Так как (sin30^0=frac12), то (R=frac a{2sin30^0}=frac a{2·frac12}=frac a1). Получаем формулу радиуса окружности, описанной около правильного шестиугольника:
Формула 2
R=a
где R — радиус описанной окружности,
а — сторона правильного шестиугольника.
Примечание 1
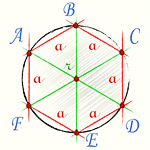
Эту же формулу модно найти и другим способом. Биссектрисы углов правильного шестиугольника разбивают его на шесть равных равносторонних треугольников. Точка пересечения биссектрис у правильного шестиугольника совпадает с точкой пересечения срединных перпендикуляров и является центром описанной окружности. Расстояние между центром окружности и вершиной шестиугольника равно радиусу описанной окружности и стороне равностороннего треугольника. Этот отрезок также равен стороне шестиугольника.
Свойства окружности, описанной около шестиугольника
- У правильного шестиугольника центры вписанной и описанной окружностей совпадают.
- Диаметр описанной окружности совпадает с большей диагональю правильного шестиугольника и равен его удвоенной стороне.
Площадь круга, ограниченного описанной окружностью
Чтобы вычислить площадь круга, ограниченного описанной окружностью правильного шестиугольника, используем стандартную формулу площади круга.
Формула 3
(S=π·r^2)
где S — площадь круга,
π — коэффициент, число π,
r — радиус круга.
Так как радиус круга равен стороне правильного шестиугольника, около которого описана окружность, получаем формулу:
Формула 4
(S=π·а^2)
где S — площадь круга,
π — коэффициент, число π,
а — сторона правильного шестиугольника.
Пример расчета радиуса окружности, описанной около шестиугольника
Задача
Дано: около правильного шестиугольника описана окружность. Меньшая диагональ правильного шестиугольника равна (5sqrt3 см.)
Найти: радиус описанной окружности.
Решение: Обозначим сторону правильного шестиугольника как а. Тогда его меньшая диагональ будет (аsqrt3 см). Следовательно, а=5 см. Радиус окружности, описанной около правильного шестиугольника равен его стороне. R=5 см.
Ответ: 5 см.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Радиус описанной окружности шестиугольника, формула
Для расчета радиуса описанной окружности шестиугольника используем формулу радиуса описанной окружности правильного многоугольника
[R = frac{a}{2 sin(frac{360°}{12})} = frac{a}{2 sin(30°)} = a]
(a – сторонa правильного шестиугольника; R – радиус описанной окружности правильного шестиугольника)
Также можно пойти другим путем. Если соединить все вершины правильного шестиугольника через центр, станет видно, что правильный шестиугольник состоит из 6-ти правильных треугольников, т.е.
[R = frac{a}{2 sin(π/6)} = a]
Вычислить, найти радиус описанной окружности шестиугольника по формуле (2)
Радиус описанной окружности шестиугольника |
стр. 253 |
|---|
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;
каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ) .
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .
Гексагон
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>normalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>normalsize),
где (p) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
[spoiler title=”источники:”]
http://shkolkovo.net/theory/77
http://calcsbox.com/post/geksagon.html
[/spoiler]
Радиус вписанной окружности в правильный шестиугольник
a – сторона шестиугольника
Формула радиуса вписанной окружности в шестиугольник, (r):
Калькулятор – вычислить, найти радиус вписанной окружности в шестиугольник
- Подробности
-
Автор: Administrator
-
Опубликовано: 10 сентября 2011
-
Обновлено: 13 августа 2021