| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
радиус:сходимости:sum_{n=0}^{infty}frac{x^{n}}{n!}
-
радиус:сходимости:sum_{n=1}^{infty}nx^{n}
-
радиус:сходимости:sum_{n=1}^{infty}frac{(x-3)^n}{n}
-
радиус:сходимости:sum_{n=0}^{infty}x^{n}
- Показать больше
Описание
Шаг за шагом найти радиус сходимости степенного ряда
radius-of-convergence-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
The Art of Convergence Tests
Infinite series can be very useful for computation and problem solving but it is often one of the most difficult…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Назначение сервиса. Онлайн калькулятор предназначен нахождения области сходимости степенного ряда. Результаты вычисления оформляются в формате Word (см. пример).
Например, исходный ряд 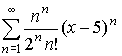 подразделяется на три части: n^n, 2^n*n!, (x-5)^n.
подразделяется на три части: n^n, 2^n*n!, (x-5)^n.
Правила ввода функций:
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, (x-4)n, записываем как(x-4)^n. - Число π ≡ pi, корень квадратный √¯ ≡ sqrt. Например, sqrt(n^2+n), en = exp(n)
Пример. 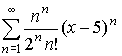 .
.
Решение.
Общий вид степенного ряда 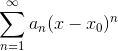 . В нашем случае x0=5,
. В нашем случае x0=5, 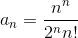 .
.
Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости R:
|x-x0|<R или x0-R<x<x0+R
Сходимость ряда на границах (при x=x0±R) необходимо исследовать дополнительно.
Найдем радиус сходимости ряда, используя формулу Даламбера:
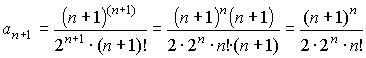 ;
;
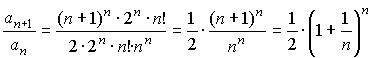 ;
;
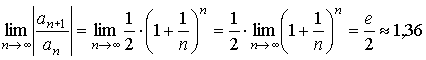 .
.
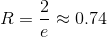
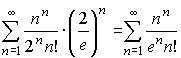 .
.
Для исследования сходимости этого ряда используем формулу Стирлинга 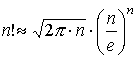 , верную для факториалов больших чисел.
, верную для факториалов больших чисел.
Получим ряд сравнения. Этот ряд расходится.
Проверим сходимость ряда при 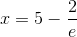 . Подставляя это значение в исходный ряд, получим числовой ряд
. Подставляя это значение в исходный ряд, получим числовой ряд
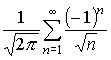 .
.
Этот ряд сходится (по признаку Лейбница).
Итак, мы получили область сходимости исходного ряда:
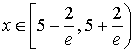 .
.
Пример 1:
Найти область сходимости ряда:

Решение от преподавателя:

Пример 2:
Найти область сходимости ряда:

Решение от преподавателя:

Пример 3:
Найти область сходимости ряда:

Решение от преподавателя:
Областью сходимости степенного ряда является интервал (-R;R), где: 
R – радиус сходимости. Вычислим его: 
x1 = 2 – 1 = 1
x2 = 2 + 1 = 3
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (1;3)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = 1
Получаем ряд: 
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется 
б) По второму признаку Лейбница предел ряда должен стремится к 0. 
Второе условие Лейбница выполняется.
Ряд сходится, значит, x = 1 – точка сходимости.
При x = 3
получаем ряд: 
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл: 
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 3 – точка расходимости.
Таким образом, данный степенной ряд является сходящимся при x [1;3)
Пример 4:
Исследовать область сходимости функционального ряда:![]()
Решение от преподавателя:

Пример 5:
Найти область сходимости степенного ряда:

Решение от преподавателя:


Пример 6:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  , при этом члены ряда не определены при х=-3/11, а если х≠-3/11, то
, при этом члены ряда не определены при х=-3/11, а если х≠-3/11, то

при любом х – ряд расходится всюду.
Пример 7:
Найти область сходимости ряда:
![]()
Решение от преподавателя:
Областью сходимости степенного ряда является интервал (-R;R), где: ![]()
R – радиус сходимости. Вычислим его: 
x1 = -1 – 2 = -3
x2 = -1 + 2 = 1
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-3;1)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = -3
Получаем ряд: ![]()
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие не выполняется
1<2<3
б) По второму признаку Лейбница предел ряда должен стремится к 0. ![]()
Второе условие Лейбница не выполняется.
Ряд расходится, значит, x = -3 – точка расходимости.
При x = 1
получаем ряд: ![]()
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
![]()
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 1 – точка расходимости.
Таким образом, данный степенной ряд является сходящимся при x (-3;1)
Пример 8:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  , при этом
, при этом

Следовательно, ряд сходится, если

и расходится, если

Если x=4/9, то ряд принимает вид  – знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
– знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
Если x=2/3, то ряд принимает вид  – такой ряд расходится (по признаку сравнения, т.к.
– такой ряд расходится (по признаку сравнения, т.к.  и ряд
и ряд  расходится (гармонический ряд)).
расходится (гармонический ряд)).
Окончательно получаем область сходимости исходного ряда: [4/9;2/3).
Пример 9:
Найдите множество абсолютной (условной) сходимости ряда:

Решение от преподавателя:

Пример 10:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  , при этом
, при этом

Следовательно, ряд сходится, если

и расходится, если

Если x=-3/7, то ряд принимает вид  – знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
– знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
Если x=-1/7, то ряд принимает вид  – такой ряд также сходится (обобщенный гармонический ряд с параметром p=11>1).
– такой ряд также сходится (обобщенный гармонический ряд с параметром p=11>1).
Окончательно получаем область сходимости исходного ряда: [-3/7;-1/7].
Пример 11:
Найдите множества абсолютной (условной) сходимости ряда

Решение от преподавателя:
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
Проверяем выполнение признака Лейбница:
Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю, то ряд сходится.
Ряд знакочередующийся. Составим ряд из абсолютных величин членов данного ряда

По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется

Второе условие Лейбница выполняется.
Данный ряд сходится, так как удовлетворяет условиям признака Лейбница для знакочередующихся рядов.
Следовательно, ряд условно сходящийся.
Следовательно, сходится условно и исходный ряд.
Область сходимости ряда:(-∞; +∞)
Пример 12:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  – обобщенный гармонический ряд с параметром
– обобщенный гармонический ряд с параметром  .
.
Такой ряд сходится, если

Однако  и поэтому
и поэтому  при любом х – ряд всюду расходится.
при любом х – ряд всюду расходится.
Пример 13:
Найти область сходимости ряда:

Решение от преподавателя:

По признаку Лейбница ряд расходится
Т. о., область сходимости имеет вид (-1; 1)
Пример 14:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  , при этом
, при этом

Следовательно, ряд сходится, если

и расходится, если

Если x=1/6, то ряд принимает вид  – такой ряд расходится (не выполнено необходимое условие сходимости).
– такой ряд расходится (не выполнено необходимое условие сходимости).
Если x=3/2, то ряд принимает вид  – такой ряд также расходится (также не выполнено необходимое условие сходимости).
– такой ряд также расходится (также не выполнено необходимое условие сходимости).
Окончательно получаем область сходимости исходного ряда:  .
.
Пример 15:
Найти область сходимости ряда:

Решение от преподавателя:

Сходимость степенного ряда.
Радиус и область сходимости степенного ряда
Краткая теория
Функциональным рядом называется ряд вида:
где
– функции,
определенные на некотором множестве
.
Множество
всех
точек сходимости ряда (*) называется его областью
сходимости.
В области сходимости
определены функции:
( n-я частичная сумма ряда)
(сумма ряда)
(остаток ряда)
Ряд
называется абсолютно сходящимся, если
сходится ряд
Из всех функциональных рядов наиболее
часто применяют степенные ряды, которыми называют ряды вида
Действительные числа
называют коэффициентами ряда.
Неотрицательное число
,
такое, что ряд (**) сходится в интервале
и расходится вне этого интервала, называется
радиусом сходимости этого ряда, а интервал
– интервалом сходимости ряда.
Радиус сходимости степенного ряда можно
найти по формулам:
или
Свойства степенных рядов
1. Сумма степенного ряда при всех
значениях
из интервала сходимости есть непрерывная
функция.
2. Степенной ряд в его интервале
сходимости можно почленно дифференцировать, то есть:
3. Степенной ряд можно интегрировать по
любому отрезку, содержащемуся в интервале сходимости, причем:
Пример решения задачи
Задача
Найдите
область сходимости степенного ряда:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Радиус
сходимости степенного ряда можно найти по формуле:
В
нашем случае:
Интервал
сходимости:
Исследуем сходимость ряда
на концах интервала:
При
Это
знакопеременный ряд.
-абсолютные величины членов ряда монотонно
убывают
По
признаку Лейбница ряд сходится
При
Это
ряд Дирихле – сходится, так как показатель степени в знаменателе больше единицы
Область
сходимости:
Ответ:
.
Пример 1.
Найти область сходимости степенного
ряда:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)![]() ;
;
д)
![]() .
.
а)
Найдем радиус сходимости R.
Так как
![]() ,
,![]() ,
,
то
 .
.
Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству
![]() ,
,
то есть интервал сходимости ряда![]() .
.
Исследуем на
сходимость данный ряд на концах интервала
сходимости.
При ![]() получаем
получаем
числовой ряд
![]() .
.
Этот ряд сходится, так как является
обобщенным гармоническим рядом![]() при
при![]() .
.
При ![]() получаем
получаем
числовой ряд
![]() .
.
Этот ряд абсолютно сходящийся, так как
ряд, составленный из абсолютных величин
его членов![]() ,
,
сходящийся.
Итак, область
сходимости данного ряда
![]() .
.
б)
Найдем радиус
сходимости R.
Так как
![]() ,
,
то .
.
Итак, интервал
сходимости ряда
![]() .
.
Исследуем на
сходимость данный ряд на концах интервала
сходимости.
При
![]() имеем числовой ряд
имеем числовой ряд
![]() .
.
Этот ряд расходящийся, так как![]() .
.
При
![]() имеем числовой ряд
имеем числовой ряд
![]() .
.
Этот ряд расходящийся, так как![]()
не существует.
Итак, область
сходимости данного ряда
![]() .
.
в)
Найдем радиус
сходимости R.
Так как
![]() ,
,![]() то
то .
.
Итак, интервал
сходимости
![]() .
.
Область сходимости данного ряда совпадает
с интервалом сходимости, то есть ряд
сходится при любом значении переменнойx.
г)
Найдем радиус сходимости R.
Так как
![]() ,
,![]() то
то![]() .
.
Так как
![]() ,
,
то ряд сходится только в точке![]() .
.
Значит, область сходимости данного ряда
представляет собой одну точку![]() .
.
д)
Найдем радиус сходимости R.
Так как
![]() ,
,![]() ,
,
то
 .
.
Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству
![]() ,
,
то есть![]() .
.
Отсюда
![]() − интервал сходимости,
− интервал сходимости,![]() − радиус сходимости.
− радиус сходимости.
Исследуем данный
ряд на сходимость на концах интервала
сходимости.
При
![]() получаем числовой ряд
получаем числовой ряд
![]() ,
,
который
расходится (гармонический ряд).
При
![]() получаем числовой ряд
получаем числовой ряд![]() ,
,
который сходится условно (ряд сходится
по признаку Лейбница, а ряд, составленный
их абсолютных величин его членов,
расходится, так как является гармоническим).
Итак, область
сходимости ряда
![]() .
.
2.3. Ряды Тейлора и Маклорена.
Разложение
функций в степенной ряд.
Приложение
степенных рядов к приближенным вычислениям
Примеры решения задач
Пример 1.
Разложить в степенной ряд функции:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)![]() .
.
а)
Заменив в формуле
![]() x
x
на
![]() ,
,
получим искомое разложение:
![]() ,
,
где ![]()
или
![]() .
.
б)
Заменяя в равенстве
![]() ,
,
где ![]()
x
на
![]() ,
,
получим искомое разложение:
![]() .
.
в)
Данную функцию можно записать так: ![]() .
.
Чтобы найти искомый ряд, достаточно в
разложение
![]() .,
.,
где ![]()
подставить ![]() .
.
Тогда получим:

или
![]() .
.
г)
Данную функцию можно переписать так:
![]() .
.
Функцию ![]()
можно разложить в степенной ряд, положив
в биномиальном ряде ![]() ,
,
получим ![]() .
.
![]() ,
,
где ![]() .
.
Чтобы получить
искомое разложение, достаточно перемножить
полученные ряды (ввиду абсолютной
сходимости этих рядов).
Следовательно,
![]()
![]() ,
,
где ![]() .
.
Пример 2.
Найти приближенные значения данных
функций:
а) ![]()
с точностью до 0,0001;
б) ![]()
с точностью до 0,00001.
а)
Так как ![]() ,
,
то в разложение функции ![]() ,
,
где ![]() подставим
подставим ![]() :
:
 или
или ![]()
Так как ![]() ,
,
то требуемая точность будет обеспечена,
если ограничиться только первыми двумя
членами полученного разложения.
Итак,
![]() .
.
б)
![]() .
.
Используем
биномиальный ряд
![]() .,
.,
где ![]() .
.
Полагая ![]()
и ![]() ,
,
получим следующее разложение:
![]()
или
![]() .
.
Если в последнем
знакочередующемся ряде учитывать только
первые два члена, а остальные отбросить,
то погрешность при вычислении ![]()
не превысит по абсолютной величине
0,000006. Тогда погрешность при вычислении
![]()
не превысит числа ![]() .
.
Следовательно,
![]() .
.
Пример 3.
Вычислить с точностью до 0,001:
а)  ; б)
; б)
 .
.
а)
 .
.
Разложим
подынтегральную функцию в степенной
ряд. Для этого подставим в биномиальный
ряд ![]()
и заменим x
на ![]() :
:
![]() .
.
Так как отрезок
интегрирования ![]()
принадлежит области сходимости
полученного ряда ![]() ,
,
то будем интегрировать почленно в
указанных пределах:

![]() .
.
В полученном
знакочередующемся ряде четвертый член
по абсолютной величине меньше 0,001.
Следовательно, требуемая точность будет
обеспечена, если учитывать только первые
три члена ряда.
 .
.
Так как первый из
отброшенных членов имеет знак минус,
то полученное приближенное значение
будет с избытком. Поэтому ответ с
точностью до 0,001 равен 0,487.
б)
Предварительно представим подынтегральную
функцию в виде степенного ряда. Заменим
в разложении функции
![]() ,
,
где ![]()
x
на
![]() ,
,
получим:
![]()
Тогда
![]() .
.

![]() .
.
Полученный
знакочередующийся ряд удовлетворяет
условиям признака Лейбница. Четвертый
член ряда по абсолютной величине меньше
0,001. Чтобы обеспечить требуемую точность,
достаточно найти сумму первых трех
членов.
Следовательно,  .
.
Соседние файлы в папке Матаматика
- #
- #
- #
- #
- #
- #

