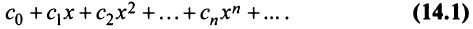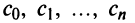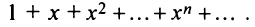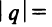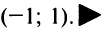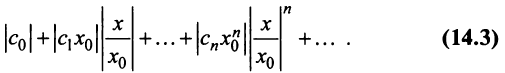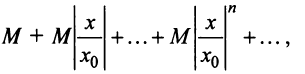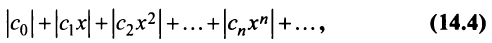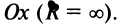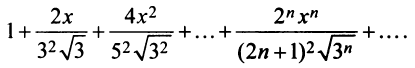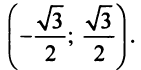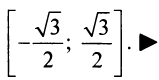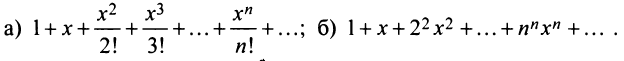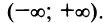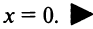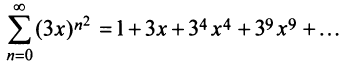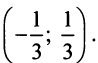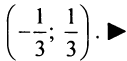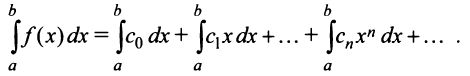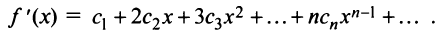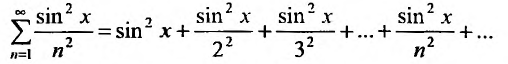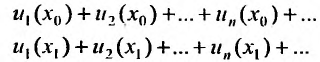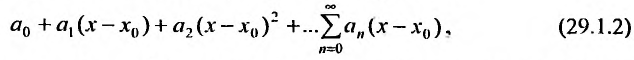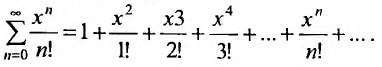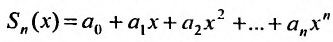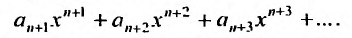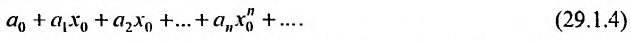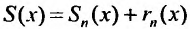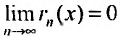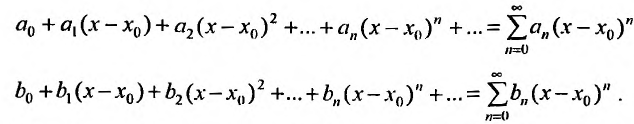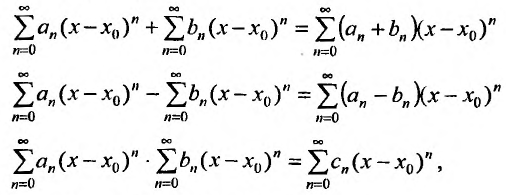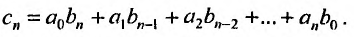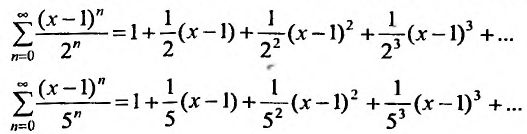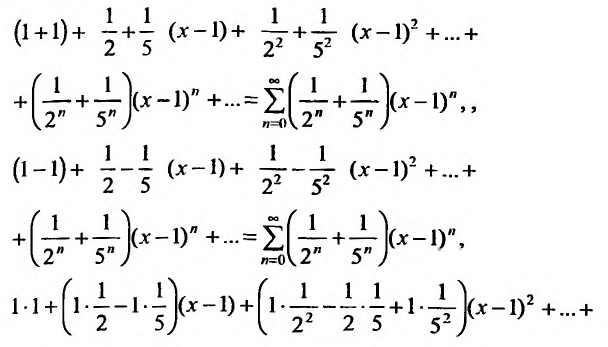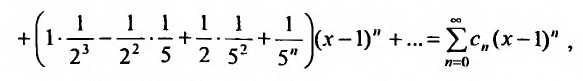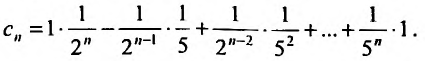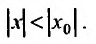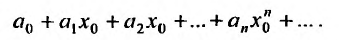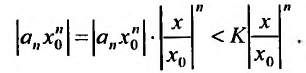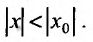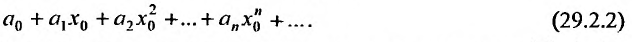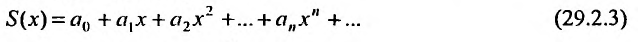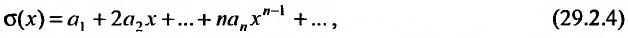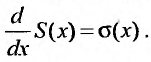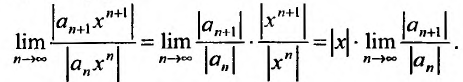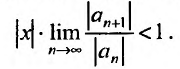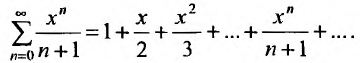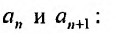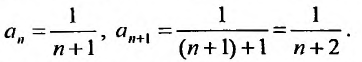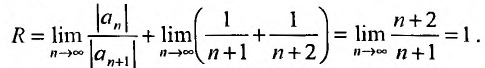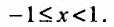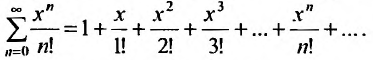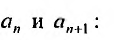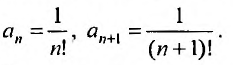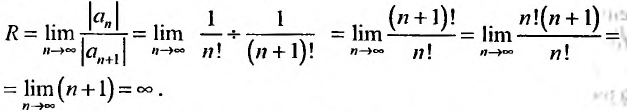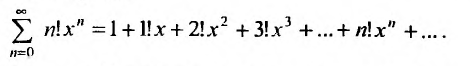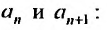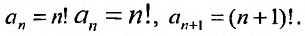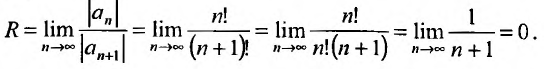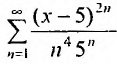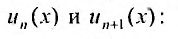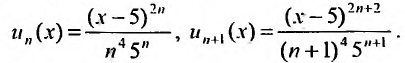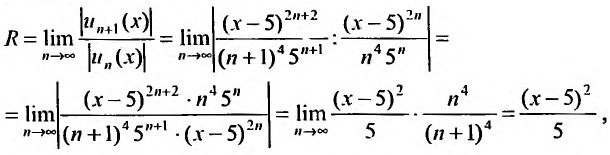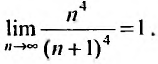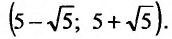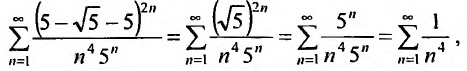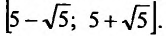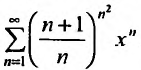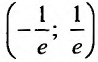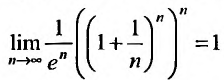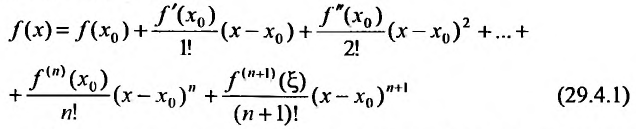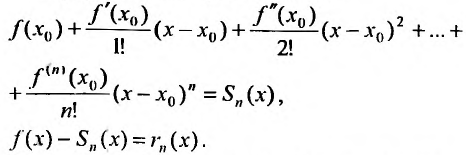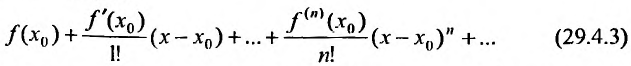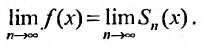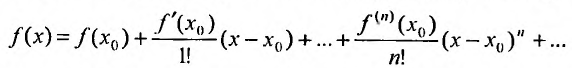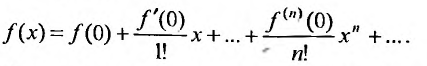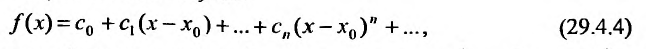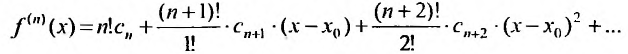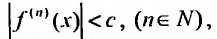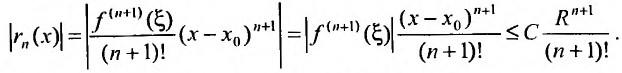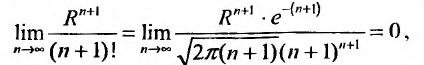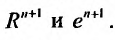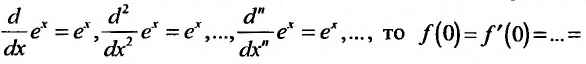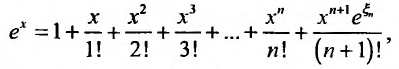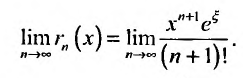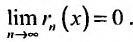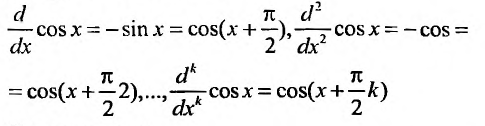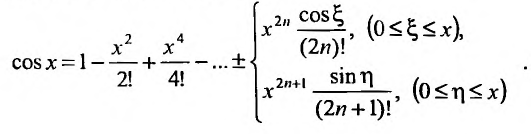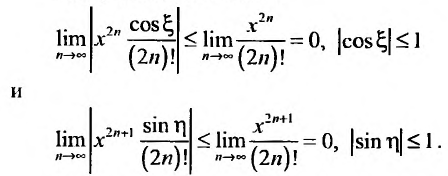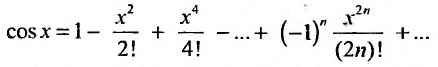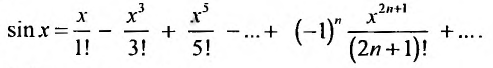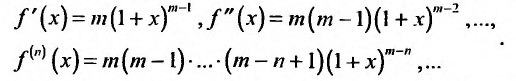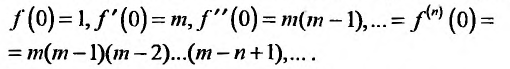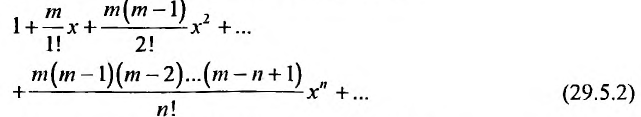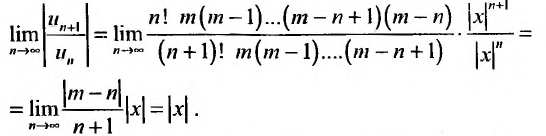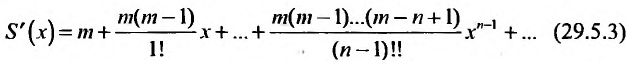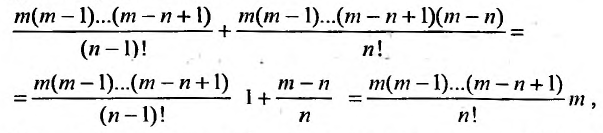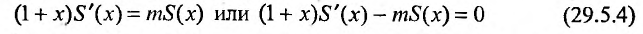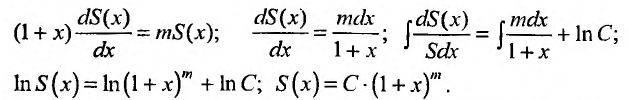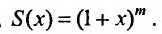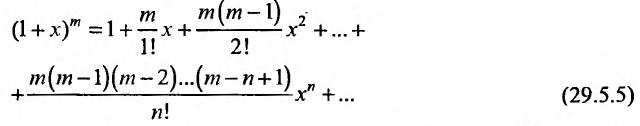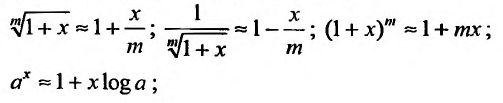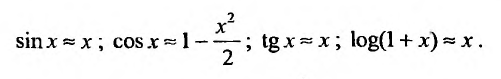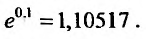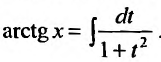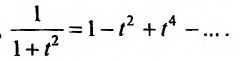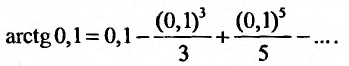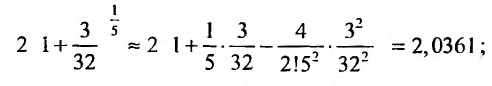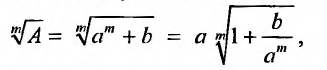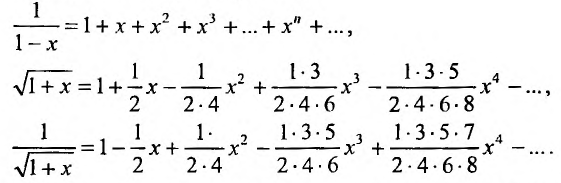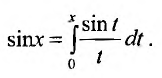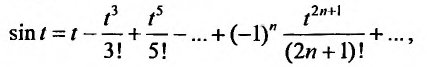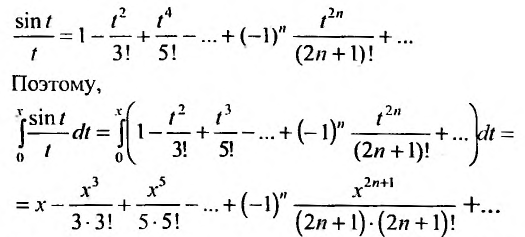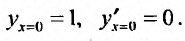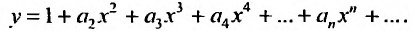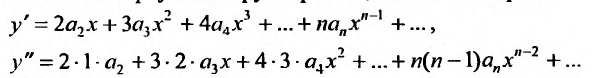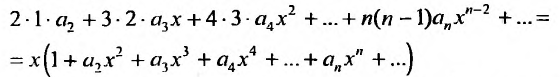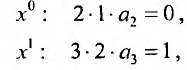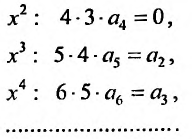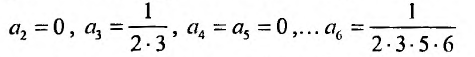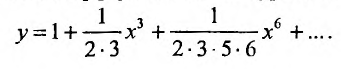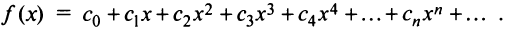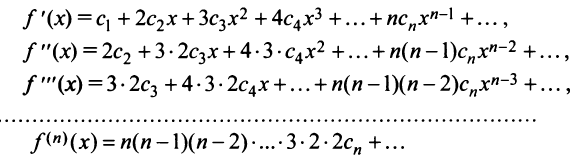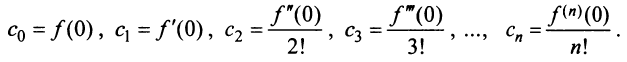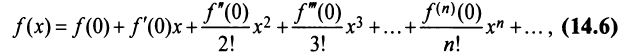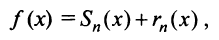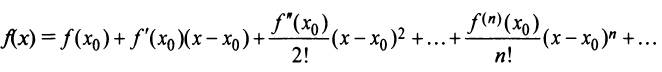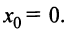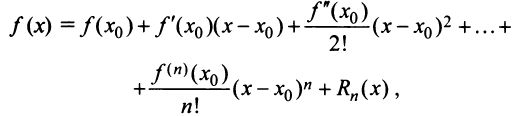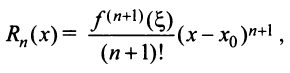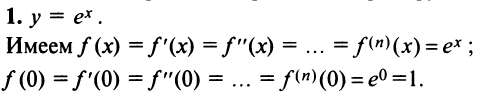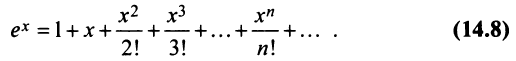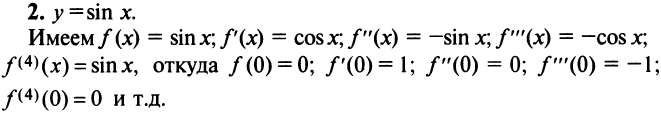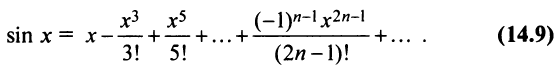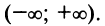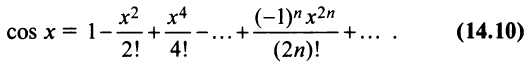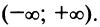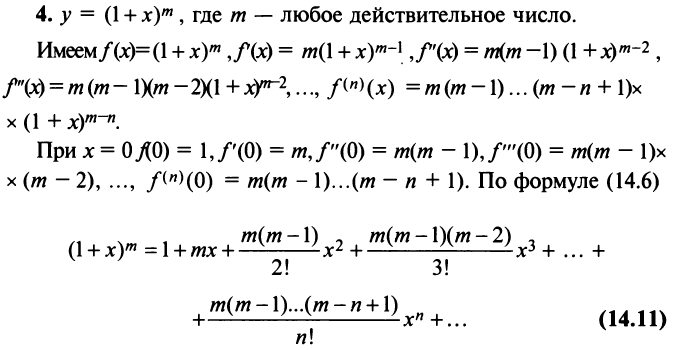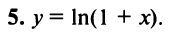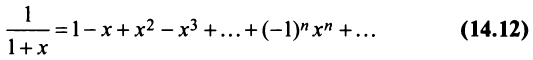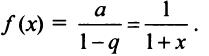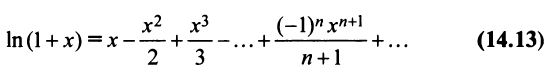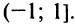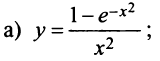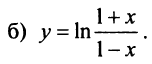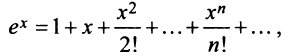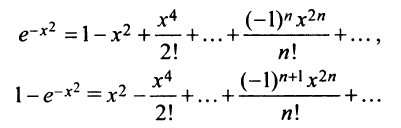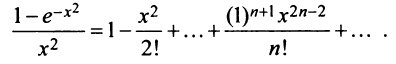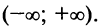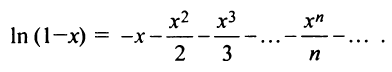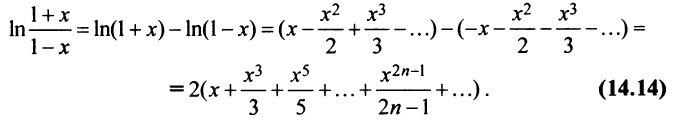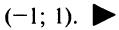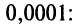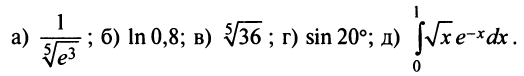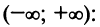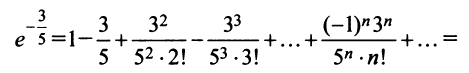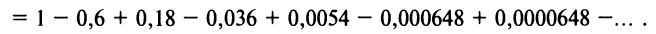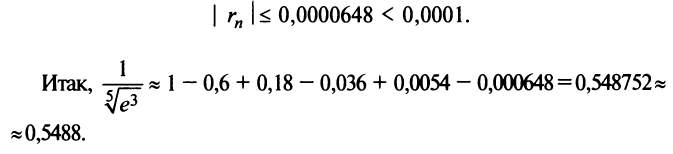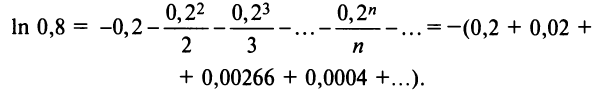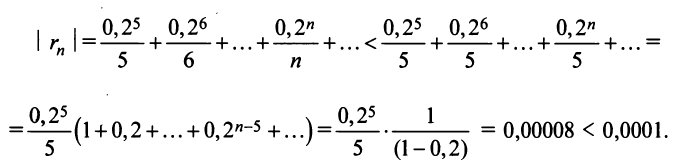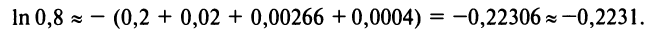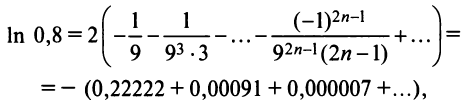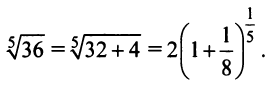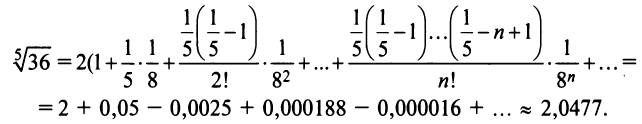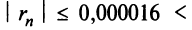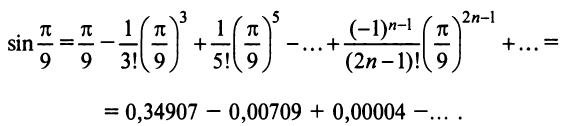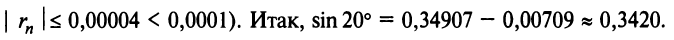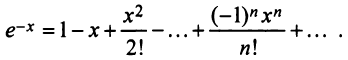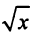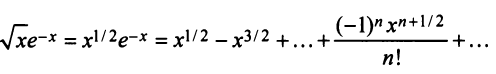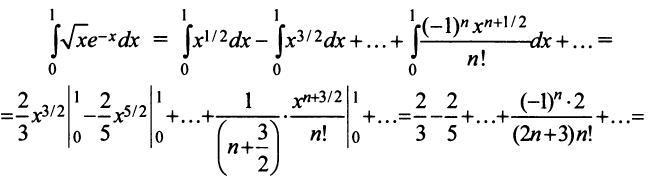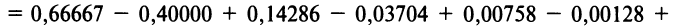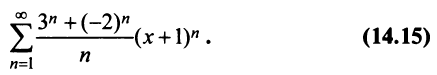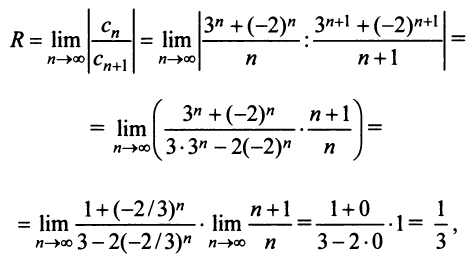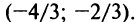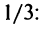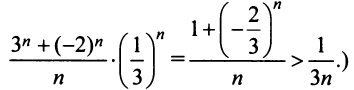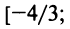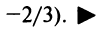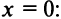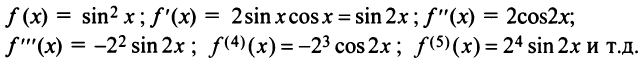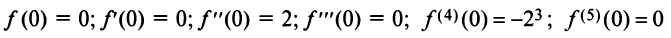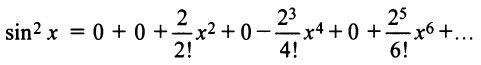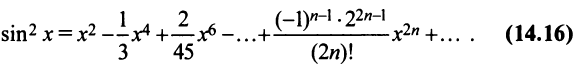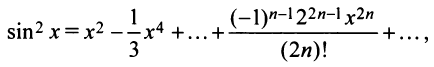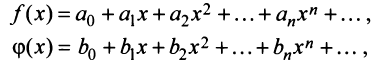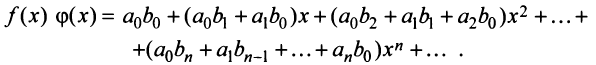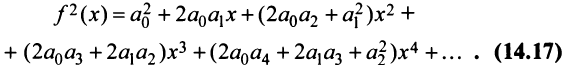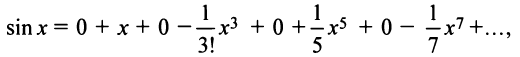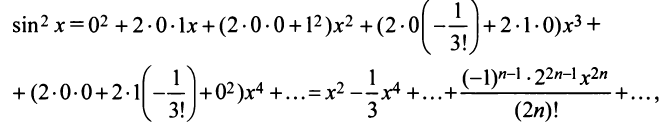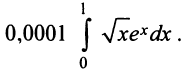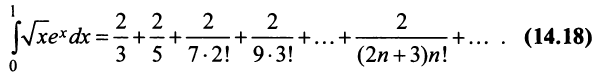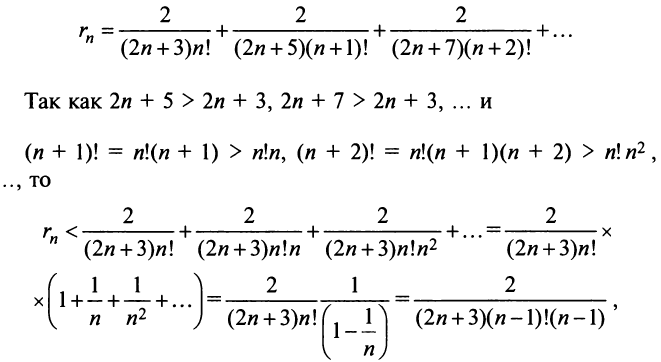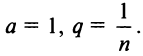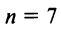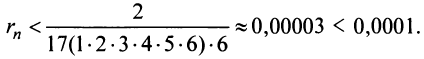Пример 1.
Найти область сходимости степенного
ряда:
а)
; б)
;
в)
; г)
;
д)
.
а)
Найдем радиус сходимости R.
Так как
,
,
то

Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству
,
то есть интервал сходимости ряда.
Исследуем на
сходимость данный ряд на концах интервала
сходимости.
При получаем
числовой ряд
.
Этот ряд сходится, так как является
обобщенным гармоническим рядомпри
.
При получаем
числовой ряд
.
Этот ряд абсолютно сходящийся, так как
ряд, составленный из абсолютных величин
его членов,
сходящийся.
Итак, область
сходимости данного ряда
.
б)
Найдем радиус
сходимости R.
Так как
,
то
Итак, интервал
сходимости ряда
.
Исследуем на
сходимость данный ряд на концах интервала
сходимости.
При
имеем числовой ряд
.
Этот ряд расходящийся, так как.
При
имеем числовой ряд
.
Этот ряд расходящийся, так как
не существует.
Итак, область
сходимости данного ряда
.
в)
Найдем радиус
сходимости R.
Так как
,
то

Итак, интервал
сходимости
.
Область сходимости данного ряда совпадает
с интервалом сходимости, то есть ряд
сходится при любом значении переменнойx.
г)
Найдем радиус сходимости R.
Так как
,
то
.
Так как
,
то ряд сходится только в точке.
Значит, область сходимости данного ряда
представляет собой одну точку.
д)
Найдем радиус сходимости R.
Так как
,
,
то

Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству
,
то есть.
Отсюда
− интервал сходимости,
− радиус сходимости.
Исследуем данный
ряд на сходимость на концах интервала
сходимости.
При
получаем числовой ряд
,
который
расходится (гармонический ряд).
При
получаем числовой ряд
,
который сходится условно (ряд сходится
по признаку Лейбница, а ряд, составленный
их абсолютных величин его членов,
расходится, так как является гармоническим).
Итак, область
сходимости ряда
.
2.3. Ряды Тейлора и Маклорена.
Разложение
функций в степенной ряд.
Приложение
степенных рядов к приближенным вычислениям
Примеры решения задач
Пример 1.
Разложить в степенной ряд функции:
а)
; б)
;
в)
; г)
.
а)
Заменив в формуле
x
на
,
получим искомое разложение:
,
где
или
.
б)
Заменяя в равенстве
,
где
x
на
,
получим искомое разложение:
.
в)
Данную функцию можно записать так: .
Чтобы найти искомый ряд, достаточно в
разложение
.,
где
подставить .
Тогда получим:
или
.
г)
Данную функцию можно переписать так:
.
Функцию
можно разложить в степенной ряд, положив
в биномиальном ряде ,
получим .
,
где .
Чтобы получить
искомое разложение, достаточно перемножить
полученные ряды (ввиду абсолютной
сходимости этих рядов).
Следовательно,
,
где .
Пример 2.
Найти приближенные значения данных
функций:
а)
с точностью до 0,0001;
б)
с точностью до 0,00001.
а)
Так как ,
то в разложение функции ,
где подставим
:

Так как ,
то требуемая точность будет обеспечена,
если ограничиться только первыми двумя
членами полученного разложения.
Итак,
.
б)
.
Используем
биномиальный ряд
.,
где .
Полагая
и ,
получим следующее разложение:
или
.
Если в последнем
знакочередующемся ряде учитывать только
первые два члена, а остальные отбросить,
то погрешность при вычислении
не превысит по абсолютной величине
0,000006. Тогда погрешность при вычислении
не превысит числа .
Следовательно,
.
Пример 3.
Вычислить с точностью до 0,001:
а) 

а)

Разложим
подынтегральную функцию в степенной
ряд. Для этого подставим в биномиальный
ряд
и заменим x
на :
.
Так как отрезок
интегрирования
принадлежит области сходимости
полученного ряда ,
то будем интегрировать почленно в
указанных пределах:
.
В полученном
знакочередующемся ряде четвертый член
по абсолютной величине меньше 0,001.
Следовательно, требуемая точность будет
обеспечена, если учитывать только первые
три члена ряда.

Так как первый из
отброшенных членов имеет знак минус,
то полученное приближенное значение
будет с избытком. Поэтому ответ с
точностью до 0,001 равен 0,487.
б)
Предварительно представим подынтегральную
функцию в виде степенного ряда. Заменим
в разложении функции
,
где
x
на
,
получим:
Тогда
.
.
Полученный
знакочередующийся ряд удовлетворяет
условиям признака Лейбница. Четвертый
член ряда по абсолютной величине меньше
0,001. Чтобы обеспечить требуемую точность,
достаточно найти сумму первых трех
членов.
Следовательно, 
Соседние файлы в папке Матаматика
- #
- #
- #
- #
- #
- #
Содержание:
Степенные ряды:
До сих пор мы рассматривали ряды, членами которых были числа, т.е. числовые ряды. Теперь перейдем к рассмотрению рядов, членами которых являются функции, в частности степенные функции
Такие ряды называются степенными, а числа
Область сходимости степенного ряда
Совокупность тех значений 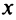
Пример:
Найти область сходимости степенного ряда
Решение:
Данный ряд можно рассматривать как геометрический ряд со знаменателем 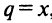
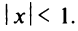
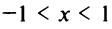
Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.
Теорема Абеля. 1) Если степенной ряд сходится при значении 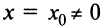
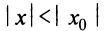
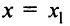
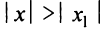
1) По условию ряд (14.1) сходится при 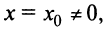
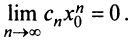
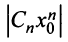
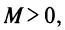
Рассмотрим ряд, составленный из абсолютных величин членов ряда (14.1) 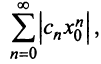
Члены ряда (14.3) согласно неравенству (14.2) меньше соответствующих членов ряда
представляющего геометрический ряд, который сходится, когда его знаменатель 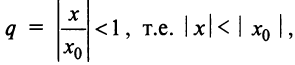
2) По условию ряд (14.1) расходится при 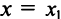
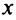
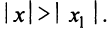
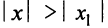
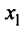
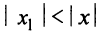
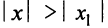
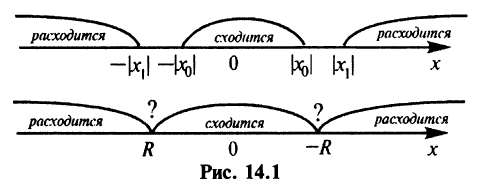
Из теоремы Абеля (см. рис. 14.1) следует, что существует такое число 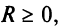
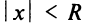
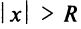
Число 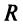
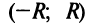
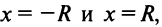
Найдем выражение радиуса сходимости степенного ряда (14.1) через его коэффициенты. Рассмотрим ряд, составленный из абсолютных величин его членов
в котором все коэффициенты 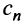
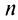
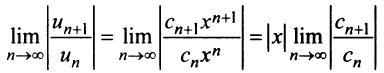
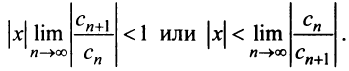
Замечание. Следует отметить, что у некоторых рядов интервал сходимости вырождается в точку 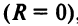
Пример:
Найти область сходимости степенного ряда
Решение:
Найдем радиус сходимости ряда по формуле (14.5) 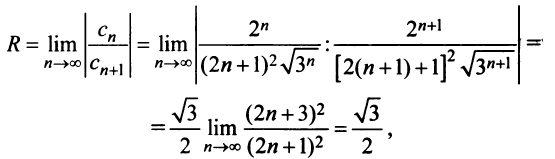
Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при 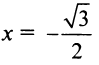
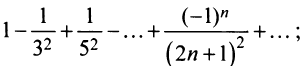
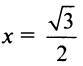
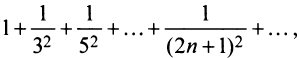
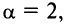
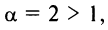
Следует отметить, что сходимость ряда на левом конце ин-тервала сходимости при 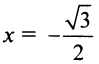
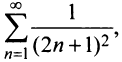
Итак, область сходимости данного ряда
Замечание. При исследовании сходимости на концах интервала сходимости для получающегося ряда с положительными членами применять признак Даламбера не имеет смысла, так как в этом случае всегда будем получать 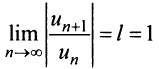
Пример:
Найти области сходимости степенных рядов:
Решение:
а) Радиус сходимости ряда по (14.5)
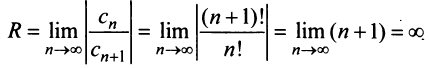
б) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что 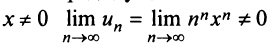
Итак, область сходимости ряда состоит из одной точки
Пример:
Найти область сходимости ряда
Решение:
Найти радиус сходимости по формуле (14.5) в данном случае не представляется возможным, так как коэффициенты ряда 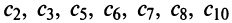
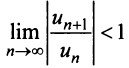
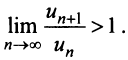
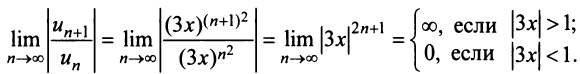
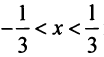
Исследуем сходимость на концах интервала сходимости: при 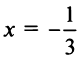
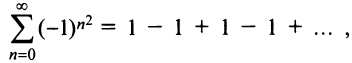
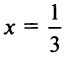
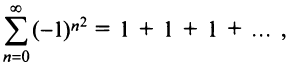
Итак, область сходимости ряда
Свойства степенных рядов. Пусть функция 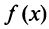
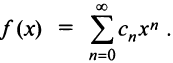
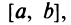
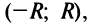
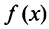
Кроме того, в интервале сходимости степенной ряд можно почленно дифференцировать:
При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости
Определение степенного ряда и его сходимости
Понятое функциональной зависимости является одним из важнейших в математике. Всякая функция осуществляет некоторое соответствие между объектами, составляющими область задания этой функции, и объектами, составляющими область её значений. Так можно рассматривать функции, которые ставят в соответствие числам – ряды. Эти функции называются функциональными рядами, т.е. функциональный ряд это выражение
членами которого являются некоторые функции переменной х. Например, ряд
является функциональным рядом.
Придавая в выражении (29.1.1) переменной х некоторые значения 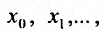
которые могут оказаться, как сходящимися, так и расходящимися.
В простейших случаях для определения сходимости ряда (29.1.1) можно применять к нему известные признаки сходимости числовых рядов, считая х фиксированным.
Определение 29.1.1. Совокупность всех значений переменной х, для которых соответствующие числовые ряды сходятся, называется областью сходимости функционального ряда (29.1.1). Определение 29.1.2. Функциональный ряд вида
где 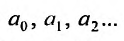
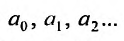
Если в ряде (29.1.2) сделать замену переменного, положив
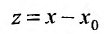
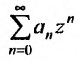
Очевидно, что исследование сходимости ряда (29.1.2) эквивалентно исследованию сходимости ряда (29.1.3). Примером степенного ряда может служить ряд
Сумма п первых членов ряда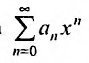
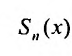
Для степенного ряда можно составить последовательность частичных сумм 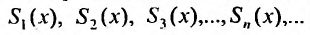
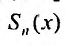
Остатком степенного ряда после n -го его члена (или n -ым остатком) называется ряд, полученный из заданного исключением n его первых членов:
Определение 29.1.3. Степенной ряд называется сходящимся на некотором множестве, если он сходится в любой точке этого множества.
Степенной ряд называется абсолютно сходящимся на некотором множестве, если в каждой точке этого множества сходится ряд из модулей его членов:
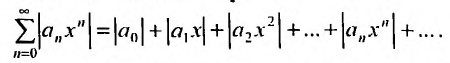
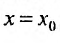
Соответствующий числовой ряд а0 +о,л:0 +… сходится абсолютно, если сходится ряд 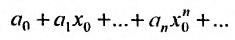
Так как каждой точке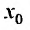
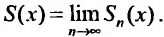
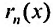
Для сходящегося степенного ряда предел остатка равен нулю:
Степенные ряды можно складывать, вычитать, умножать. Пусть заданы два степенных ряда:
Сумма, разность и произведение заданных степенных рядов определяется формулами:
где
Например, сумма, разность и произведение степенных рядов:
имеет вид:
где
Радиус сходимости, интервал сходимости
Области сходимости степенных рядов устроены довольно просто. Они описываются следующей теоремой.
Теорема 29.2.1 (теорема Абеля). Если степенной ряд
сходится при некотором 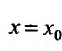
Если же степенной ряд (29.2.1) расходится при 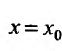
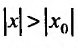
Доказательство. Предположим сначала, что степенной ряд (29.2.1) сходится в точке 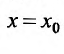
Тогда, в силу необходимого признака сходимости, 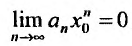
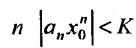
Если 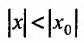
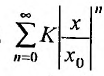
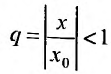
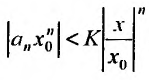
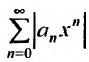
Предположим теперь, что степенной ряд (29.2.1) расходится, при 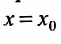
Возьмём тогда некоторое значение х, для которого 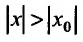
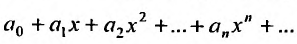
сходится. Но тогда из сходимости этого ряда, в силу первой части доказательства теоремы, вытекает сходимость ряда (29.2.2), что противоречит предположению, о его расходимости. Полученное противоречие означает, что для всех 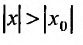
Если ряд (29.2.1) имеет вещественные коэффициенты и переменная х принимает только вещественные значения, то справедливо следующее определение, вытекающее из теоремы Абеля.
Определение 29.2.1. Величина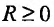
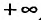
такая, что при всех х, у которых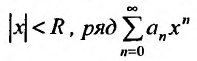
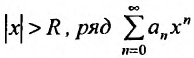
Множество точек х удовлетворяющих соотношению 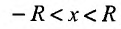
Итак, из определения 29.2.1 и теоремы Абеля следует, что областью сходимости степенного ряда – является интервал сходимости. И если значение 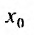
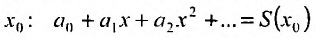
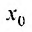
Свойства степенных рядов
Для степенных рядов справедливы следующие свойства:
1) Степенной ряд сходится равномерно внутри интервала сходимости.
2) Внутри интервала сходимости ряда сумма его является непрерывной функцией.
3) Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
4) Если степенной ряд
имеет радиус сходимости R , то и ряд
получаемый в результате почленного дифференцирования ряда (29.2.3) также имеет радиус сходимости R. Производная суммы ряда (29.2.3) равна сумме ряда (29.2.4), т.е.
Вычисление интервала сходимости
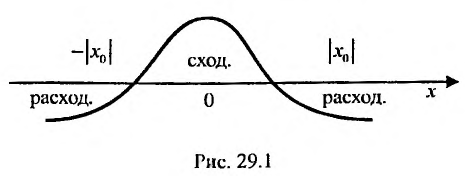
Как уже было сказано в и. 2 областью сходимости степенного ряда является интервал сходимости. Более того, из теоремы Абеля следует, что областью сходимости степенного ряда является интервал с центром в начале координат (рис 29.1).
Действительно, если 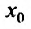
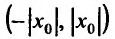
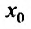
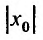
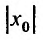
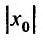
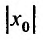
Заметим, что на концах интервала вопрос о сходимости или расходимости решается индивидуально в каждом конкретном случае. У некоторых рядов интервал сходимости может вырождаться в точку, у других охватывать всю ось Ох.
Укажем теперь способ вычисления радиуса сходимости степенного ряда.
Пусть задан степенной ряд 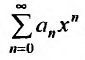
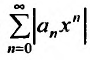
вычислим предел
Если этот предел меньше единицы, то, как следует из признака Д’Аламбера, ряд, составленный из модулей членов ряда (29.2.1) сходится, т.е. ряд сходится если
Если же 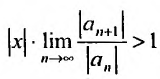
А это означает, что если 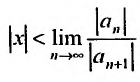
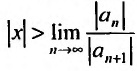
Учитывая определение радиуса сходимости степенного ряда, получим, что радиус сходимости можно вычислить по формуле:
Рассуждая аналогичным образом можно получить еще одну формулу для определения радиуса сходимости:
Если степенной ряд содержит только четные или нечетные степени х, то применяем признак Д’Аламбсра или Коши к ряду, составленному из модулей членов данного ряда.
Пример №1
Найти радиус и интервал сходимости степенного ряда:
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
Итак, степенной ряд сходится для |х| 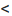
Исследуем сходимость ряда на концах интервала сходимости.
Пусть х =—1. Тогда получим знакочередующийся ряд 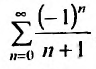
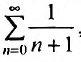
Суммируя вышесказанное, получим интервал сходимости
Пример №2
Найти радиус и интервал сходимости степенного ряда
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.2):
Так как 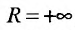
Пример №3
Найти радиус и интервал сходимости степенного ряда:
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
Так как радиус сходимости равен нулю, то ряд сходится только в одной точке x= 0.
Пример №4
Найти радиус и интервал сходимости степенного ряда
Решение:
Данный ряд содержит только четные степени (а- – 5), коэффициенты при нечетных степенях равны нулю. Поэтому воспользоваться формулами (29.3.1) и (29.3.2) не представляется возможным.
Считая х фиксированным, применим признак Д’Аламбера к ряду, составленному из модулей членов данного ряда. Выпишем значения
Тогда
так как
Ряд сходится, если 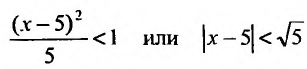
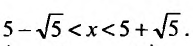
Исследуем сходимость ряда на концах интервала сходимости. Пусть 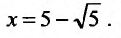
который сходится, как ряд Дирихле, для которого а = 4. При 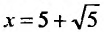
Пример №5
Найти радиус и интервал сходимости степенного ряда
Решение:
Выпишем значение 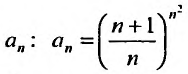
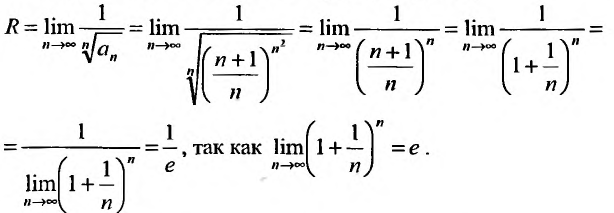
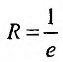
Исследуем его сходимость на концах интервала.
Пусть 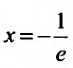
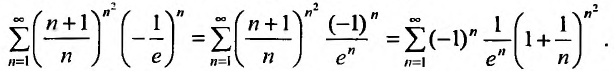
Следовательно, данный ряд расходится. И при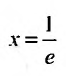
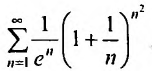
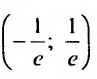
Ряды Тейлора и Маклорена
Как уже отмечалось, сумма сходящегося степенного ряда является некоторой функцией, определенной внутри интервала сходимости. В связи с этим мы рассмотрим задачу разложения некоторой функции в ряд, т.е. будем по заданной функции искать сходящийся ряд того или иного типа, сумма которого в интервале сходимости равнялась бы заданной функции.
Известно, что если функция f имеет на некотором отрезке производные всех порядков, то можно написать формулу Тейлора для любого значения n:
где 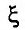
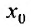
В формуле Тейлора обозначим:
пункта 27.2 (теорема 27.2.1) следует, что если
то степенной ряд
сходится и его суммой будет функция f(х), так как 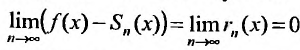
Справедливо и обратное утверждение, что если степенной ряд (29.4.3) сходится, то выполняется (29.4.2).
Определение 29.4.1. Представление функции f в виде ряда
называется разложением этой функции в ряд Тейлора. Если же 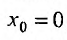
Следует заметить, что остаточный член в формуле Тейлора для функции J не обязательно является остатком ряда Тейлора для этой функции. Поэтому из сходимости ряда Тейлора для функции f , еще не следует сходимость именно к этой функции. При разложении функции в ряд Тейлора необходимо проверять условие (29.4.2). Однако сели разложение функции в какой-либо степенной ряд вообще возможно, то оно является разложением в ряд Тейлора, т.е. справедлива следующая теорема.
Теорема 29.4.1. Пусть
и стоящий справа ряд сходится в интервале 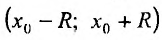
Доказательство. Так как степенной ряд в интервале сходимости можно почленно дифференцировать, то n-ую производную функции (29.4.4) можно представить в виде:
Полагая в последнем тождестве 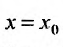
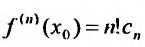
Из доказанной теоремы вытекает, что в одной и той же области, для одной и той же функции существует единственное разложение.
На практике, для разложения функции в ряд Тейлора, удобно пользоваться следующей теоремой.
Теорема 29.4.2. Если при любых х, удовлетворяющих неравенству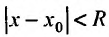
то ряд Тейлора, для этой функции, сходится в интервале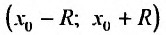
Доказательство. Из условия теоремы следует, что функцию f можно представить формулой Тейлора с остаточным членом в форме Лагранжа, т.е.
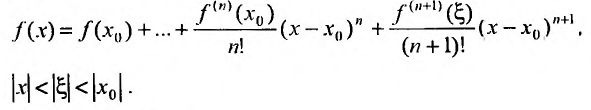
Переходя к пределу при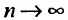
Воспользовавшись асимптотической формулой Стерлинга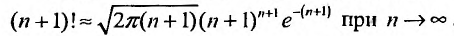
так как стспснно-показательная функция 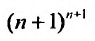
Тогда из неравенства (29.4.6) получим: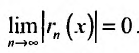
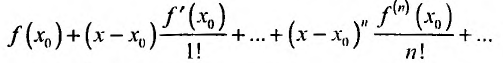
Разложение некоторых элементарных функций в ряд Маклорена
Из пункта 29.4 следует, что для того чтобы некоторая функция разлагалась в ряд Тейлора нужно, чтобы она имела производные любого порядка и чтобы либо 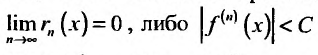
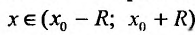
1. Разложение функции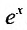
Находим производные данной функции и их значения при х=0. Так как
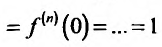
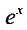
где 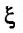
Вычислим предел остаточного члена, для любого х:
Выражение 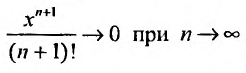
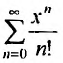
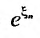
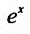
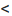
Следовательно, ряд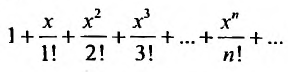
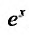
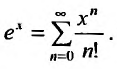
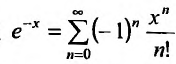
2. Разложение функций cos х и sin х. Для функции cos x имеем:
Следовательно,
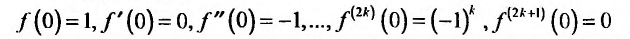
Маклорена с остаточным членом в форме Лагранжа для функции cosx имеет вид:
Ясно, что для любого X
Поэтому, функция cos л- разлагается в ряд Маклорена вида:
Аналогично получается разложение в ряд Маклорена функции sinx:
3. Биномиальный ряд.
Найдем разложение в степенной ряд функции
где m -произвольное действительное число.
Дифференцируя равенство (29.5.1) n раз, получим:
Значения функции и се производных при х = 0 равны:
Следовательно, ряд Маклорена имеет вид:
Если m- целое, то выражение (29.5.2) содержит конечное число членов. Если же m- нецелое, то выражение (29.5.2)- бесконечный ряд, называемый биномиальным.
Определим вначале радиус сходимости этого ряда, для чего применим признак Д’Аламбсра к ряду, составленному из модулей его членов:
Следовательно, при |х| 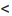
Покажем теперь, что ряд (29.5.2) сходится к функции 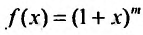
Умножим обе части (29.5.3) на 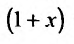
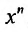
Эта сумма, как показано, равна произведению коэффициента при 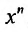
С другой стороны, вычисляя производную отношения
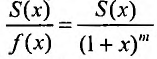
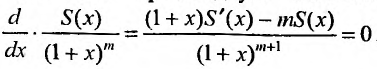
Решая дифференциальное уравнение 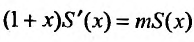
Пусть x = 0, тогда S(0) = С. Из (29.5.2) следует, что S(0) = 1, тогда С = 1.
Следовательно,
Итак, разложение
имеет место при всех х, удовлетворяющих условию 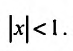
Применение рядов в приближенных вычислениях
Разложения функций в ряд Маклорена позволяют во многих случаях вычислить с большой степенью точности значения этих функций, заменяя ее конечным числом членов разложения. Чем меньше х, тем меньше членов можно брать в этом разложении для вычисления f(х) с желаемой точностью. Если х весьма мало, то достаточно ограничится первыми двумя членами, отбросив все остальные. Например, при х близких к нулю можно пользоваться следующими приближенными формулами:
Например, вычислим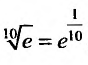
Имеем, 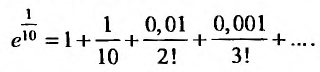
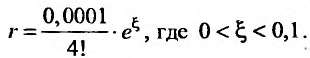
Иногда при вычислении значений функций удобно пользоваться почленным дифференцированием или интегрированием рядов.
Например, известно, что
С другой стороны,
Следовательно,
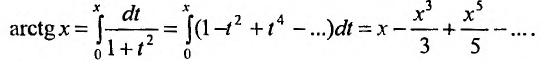
Этот ряд знакочередующийся. Поэтому, его остаток не превосходит первого «отброшенного» члена. Удерживая в разложении первых два слагаемых, получим значение arctg 0,1 = 0,09967 с пятью верными знаками.
При помощи биномиальною ряда можно быстро и довольно точно вычислять значение корней из чисел.
Пример №6
Вычислить 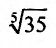
Решение:
Представим, этот корень в виде
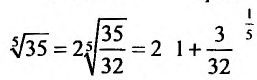
следующим член 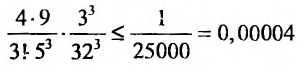
В общем случае можно записать:
где 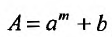
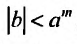
Кроме того, биномиальный ряд является основой многих дальнейших разложений функций в ряды. Например, можно найти разложение в ряд Маклорена функции:
При помощи рядов можно вычислять определенные интегралы.
Например, вычислим интегральный синус:
Имеем
тогда
Подставляя вместо x, те или иные конкретные значения переменной, мы можем вычислять интересующие нас значения интегрального синуса.
При помощи разложении в степенные ряды можно приближенно интегрировать разнообразные дифференциальные уравнения.
Например, найдем решение уравнения 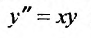
Будем искать решение этого уравнения в виде степенного ряда: 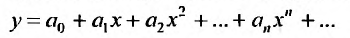
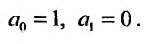
Вычислим первую и вторую производные от этого ряда:
и подставив у, 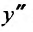
приравняем коэффициенты при равных степенях .г, предварительно умножив правую часть на х:
Получаем систему уравнений, из которой находим:
Замечаем, что отличными от нуля будут лишь те коэффициенты, у которых индекс и степень делятся на 3. Получим решение заданного дифференциального уравнения в виде:
- Заказать решение задач по высшей математике
Ряд Маклорена
Предположим, что функция 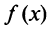
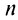
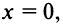
Выразим коэффициенты ряда через 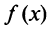
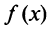
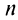
Полагая в полученных равенствах 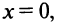
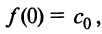
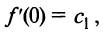
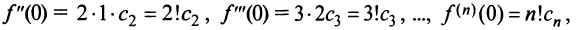
Подставляя значения коэффициентов 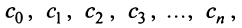
называемый рядом Маклорена.
Следует отметить, что не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд Маклорена, составленный формально для функции 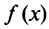
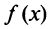
Так же как и для числовых рядов, сумму 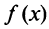
где 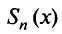
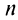
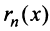
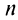
Тогда на основании свойства 4 сходящихся рядов (см. §13.1) можно сформулировать теорему.
Теорема. Для того чтобы ряд Маклорена сходился к функции 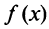
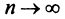
для всех значений 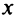
Можно доказать, что если функция 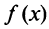
Замечание. Ряд Маклорена является частным случаем ряда Тейлора:
при
Ряд Тейлора тесно связан с формулой Тейлора.
где 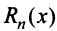
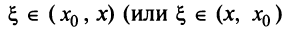
Очевидно, что при выполнении условия (14.7) остаток 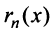
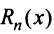
Разложение в ряд Маклорена некоторых функций
По формуле (13.6)
Область сходимости ряда 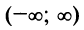
Очевидно, что производные четного порядка 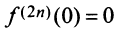
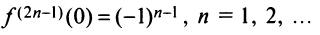
Область сходимости ряда
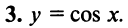
Область сходимости ряда
Интервал сходимости ряда 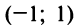
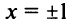
Ряд (14.11) называется биномиальным. Если 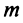
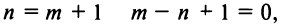
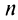
Получить разложение для этой функции можно проще, не вычисляя непосредственно коэффициенты ряда (14.6) с помощью производных.
Рассмотрим геометрический ряд
со знаменателем 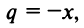
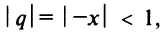
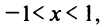
Интегрируя почленно равенство (14.12) в интервале 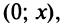
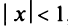
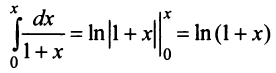
Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть
Можно доказать, что ряды, приведенные в формулах (14.8) — (14.13), сходятся к функциям, для которых они составлены.
При разложении более сложных функций используют непосредственно формулу (14.6) либо таблицу простейших разложений (14.8) – (14.13).
Пример №7
Разложить в ряд функции:
Решение:
а) Так как по (14.8)
то, заменяя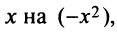
и, наконец,
Область сходимости ряда
б) В разложении 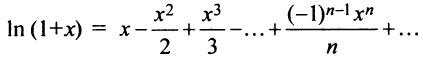
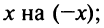
Теперь
Область сходимости ряда
Применение рядов в приближенных вычислениях
Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «неберущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.
Пример №8
Вычислить приближенно с точностью до
Решение:
а) Для вычисления 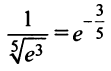
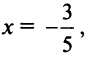
Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница (см. § 13.4) для сходящегося знакочередующегося ряда мы допустим погрешность 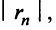
б) Для вычисления 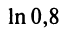
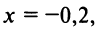
Если в качестве 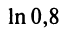
(Мы учли, что сумма сходящегося геометрического ряда в
скобках равна 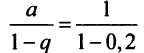
Следует отметить, что для вычисления логарифмов более удобным является ряд (14.14), который сходится быстрее ряда (14.13). Действительно, пусть 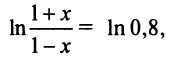
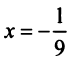
т.е. для вычисления 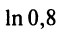
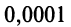
в) Представим 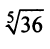
Так как 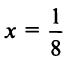
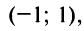
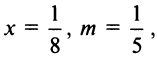
(Для обеспечения данной точности расчета необходимо взять 4 члена, так как по следствию из признака Лейбница для сходящегося знакочередующегося ряда погрешность 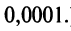
г) Для вычисления 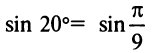
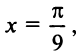
(Необходимо взять два члена, так как при этом погрешность
д)«Точное» интегрирование здесь невозможно, так как интеграл «неберущийся». Заменив 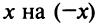
Умножая полученный ряд на
и почленно интегрируя в интервале 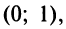
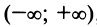
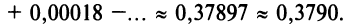
Пример №9
Исследовать сходимость ряда
Решение:
Радиус сходимости ряда (14.15), заданного по степеням 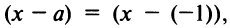
т.е. 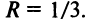
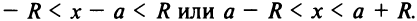
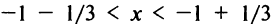
Исследуем сходимость ряда (14.15) на концах этого интервала. При 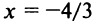
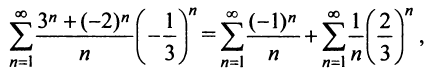
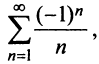
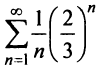
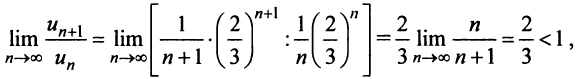
При 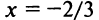
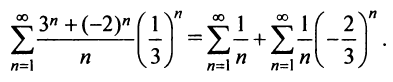
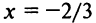
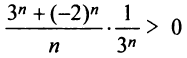
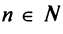
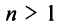
Итак, область сходимости степенного ряда (14.15)
Пример №10
Разложить в ряд Маклорена функцию
Решение:
Первый способ. Применим метод непосредственного разложения по формуле (14.6).
Вначале найдем производные до «-го порядка и вычислим их значения при
При 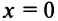
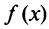
и т.д. Теперь по формуле (14.6) запишем ряд
или
Второй способ. Учитывая, что 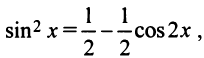
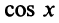
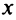

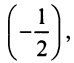
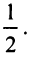
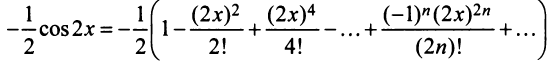
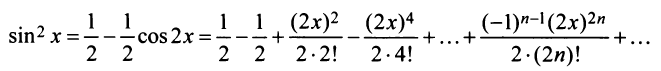
т.е. то же разложение (14.16).
Третий способ. Разложение функции 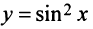
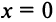
то произведение функций разлагается в той же окрестности в степенной ряд
В частности, при 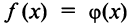
Для функции 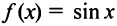
находим по формуле (14.17)
т.е. получили то же разложение (14.16).
Область сходимости ряда, как нетрудно убедиться, есть 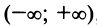
Пример №11
Вычислить с точностью до
Решение:
Выражение данного интеграла в виде числового ряда находится
Вычисление интеграла свелось не к нахождению суммы сходящегося знакочередующегося ряда, при вычислении которой погрешность оценивается с помощью следствия из теоремы Лейбница, а к определению суммы ряда с положительными членами с неизвестной оценкой погрешности.
Поступим следующим образом. Предположим, что для оценки суммы ряда мы взяли 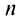
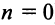
ибо выражение в круглых скобках представляет сумму сходящегося геометрического ряда (13.5) при
При
(Легко вычислить, что при любых 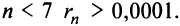
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
Круг сходимости[1] степенного ряда 
,
,
в котором ряд абсолютно сходится, а вне его, при 



Радиус сходимости[править | править код]
Радиус круга сходимости называется радиусом сходимости[1] ряда.
Радиус сходимости ряда Тейлора аналитической функции равен расстоянию от центра ряда до множества особых точек функции, и может быть вычислен по формуле Коши — Адамара:
Эта формула выводится на основе признака Коши.
Теорема Островского — Адамара[править | править код]
Для степенного ряда
,
у которого почти все коэффициенты равны нулю, в том смысле, что последовательность ненулевых коэффициентов 
для некоторого фиксированного 

Литература[править | править код]
- ↑ 1 2 Фихтенгольц Григорий Михайлович. Курс дифференциального и интегрального исчисления — 2 том. — 8. — Москва: Физматлит, 2001-. — С. 557. — 864 с. — ISBN 5-9221-0157-9.
См. также[править | править код]
- Аналитическое продолжение
Сходимость степенного ряда.
Радиус и область сходимости степенного ряда
Краткая теория
Функциональным рядом называется ряд вида:
где
– функции,
определенные на некотором множестве
.
Множество
всех
точек сходимости ряда (*) называется его областью
сходимости.
В области сходимости
определены функции:
( n-я частичная сумма ряда)
(сумма ряда)
(остаток ряда)
Ряд
называется абсолютно сходящимся, если
сходится ряд
Из всех функциональных рядов наиболее
часто применяют степенные ряды, которыми называют ряды вида
Действительные числа
называют коэффициентами ряда.
Неотрицательное число
,
такое, что ряд (**) сходится в интервале
и расходится вне этого интервала, называется
радиусом сходимости этого ряда, а интервал
– интервалом сходимости ряда.
Радиус сходимости степенного ряда можно
найти по формулам:
или
Свойства степенных рядов
1. Сумма степенного ряда при всех
значениях
из интервала сходимости есть непрерывная
функция.
2. Степенной ряд в его интервале
сходимости можно почленно дифференцировать, то есть:
3. Степенной ряд можно интегрировать по
любому отрезку, содержащемуся в интервале сходимости, причем:
Пример решения задачи
Задача
Найдите
область сходимости степенного ряда:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Радиус
сходимости степенного ряда можно найти по формуле:
В
нашем случае:
Интервал
сходимости:
Исследуем сходимость ряда
на концах интервала:
При
Это
знакопеременный ряд.
-абсолютные величины членов ряда монотонно
убывают
По
признаку Лейбница ряд сходится
При
Это
ряд Дирихле – сходится, так как показатель степени в знаменателе больше единицы
Область
сходимости:
Ответ:
.
Степенные ряды с комплексными членами и их свойства
Круг сходимости степенного ряда
Степенным рядом называется функциональный ряд (3.1), члены которого образованы степенями или
, то есть ряд вида
или
Ряд (3.9) называется рядом по степеням разности ; ряд (3.10) — рядом по степеням
. Очевидно, один ряд к другому можно преобразовать простой заменой.
Особенностью степенного ряда, как частного вида ряда (3.1), является аналитичность его членов во всей комплексной плоскости. Другая особенность связана с видом его области сходимости. В общем случае функционального ряда, областью сходимости может быть множество произвольного вида (см. примеры 3.1-3.5). Это и вся плоскость, и плоскость с выколотой точкой, и круг, и внешность круга, и полуплоскость, и кольцо, и пустое множество (ряд расходится всюду). В случае степенного ряда последнего случая быть не может — ряд имеет хотя бы одну точку сходимости. Так, ряд (3.9), очевидно, сходится в точке , а ряд (3.10) — в точке
.
В примере 3.1 определялась область сходимости степенных рядов вида (3.10). Кроме двух тривиальных случаев области сходимости — вся плоскость и только одна точка, в двух других областью сходимости оказывается круг, как и для ряда вида (3.9) из примера 3.4, п.”а”. Полученный результат не является случайным. Действительно, областью сходимости степенного ряда является круг. При этом область сходимости, состоящую из одной точки, можно рассматривать как круг радиуса , а в случае сходимости ряда во всей комплексной плоскости как круг радиуса
. Доказательство этого утверждения получается из основной теоремы теории степенных рядов — теоремы Абеля, которая формулируется и доказывается так же, как и в действительной области.
Теорема Абеля о сходимости ряда
Теорема 3.3 (теорема Абеля). Если степенной ряд (3.10) сходится в точке , то он сходится, и притом абсолютно, для любого
, удовлетворяющего неравенству
.
Как следствие этой теоремы устанавливается существование положительного числа , такого, что ряд (3.10) при
сходится, а при
расходится, т.е. окружность
разделяет плоскость на две части: внутри окружности ряд сходится, вне — расходится. Радиус этой окружности — число
— называется радиусом сходимости, круг
— кругом сходимости ряда.
Формула Коши-Адамара
Радиус сходимости степенного ряда определяется по формуле Коши-Адамара
(3.11)
Здесь — верхний предел последовательности
. Он всегда существует (конечный или бесконечный), и притом единственный. В случае
полагают
, а в случае
полагают
.
Замечания 3.1
1. Для ряда (3.9) имеем такое же утверждение: он сходится в круге , где радиус сходимости
определяется по формуле (3.11).
2. Радиус сходимости ряда можно определить иначе. Например, найти область сходимости ряда, используя формулы (3.8), а затем — радиус. Так, в примере 3.1 рассматриваются степенные ряды. Для первого из этих рядов найдена область сходимости , поэтому
, для второго из
получаем
. Для двух других рядов имеем соответственно
и
.
Пример 3.8. Доказать, что для ряда , где
для любого
, радиус сходимости можно определить по формулам:
(3.12)
Решение
Найдем область сходимости ряда, используя формулы (3.8):
Если , то неравенство
выполняется при любом
, т.е. ряд сходится всюду и
. Если
, то неравенство
не выполняется ни для какого значения
и ряд сходится только в одной точке
, то есть
.
В случае, когда предел является конечным и не равен нулю, обозначим его , то есть
. Тогда неравенство
, то есть
, выполняется для
, удовлетворяющих условию
, а это есть круг сходимости, следовательно,
. Первая из формул (3.12) доказана. Аналогично доказывается вторая.
Пример 3.9. Найти области сходимости комплексных рядов .
Решение
Радиус сходимости каждого из рядов , так как для первого ряда
и согласно (3.12)
; для второго ряда имеем
и
; для третьего из
получаем
. Поэтому областью сходимости каждого из этих рядов является круг
.
Исследуем сходимость рядов на границе круга сходимости — на окружности , или, что то же,
.
Для первого ряда в точках границы, т.е. при , получаем абсолютно сходящиеся ряды, так как
, а ряд
сходится. Следовательно, ряд
сходится во всех граничных точках. Поэтому он сходится абсолютно — круге
.
Ряд на границе расходится (см. пример 3.1, п.”а”).
Ряд , очевидно, расходится в точке
(точке границы
при
) как гармонический ряд
и сходится в точке
(точке
при
) как знакочередующийся ряд
. Заметим, что сходимость последнего ряда неабсолютная. Можно показать, что ряд расходится на границе
только при
, то есть
, а во всех других точках границы, т.е. при
, он сходится.
Заметим, что данные в примере ряды могут быть получены один из другого с помощью дифференцирования или интегрирования. Так, из ряда получаем дифференцированием ряд
или
, а из ряда
также дифференцированием — ряд
или
.
Пример 3.10. Найти радиус сходимости рядов: а) ; б)
.
Решение
Свойства степенных рядов
1. Если , т.е. ряд (3.10) сходится в круге
, то, используя признак Вейерштрасса, нетрудно установить, что ряд сходится равномерно в круге
, где
— любое положительное, меньшее
число,
. Это означает, что степенной ряд сходится равномерно внутри круга сходимости.
2. В силу аналитичности членов степенного ряда и свойств равномерно сходящихся рядов получаем (см. теорему 3.2), что внутри круга сходимости сумма степенного ряда есть функция аналитическая.
3. Степенной ряд можно почленно интегрировать и дифференцировать любое число раз внутри круга сходимости.
Последнее свойство означает, что ряд, полученный из ряда дифференцированием, т.е. ряд
или, что удобнее,
, и ряд, полученный интегрированием, т.е. ряд
, сходятся внутри круга сходимости исходного ряда, а потому их радиусы сходимости не меньше радиуса сходимости исходного ряда.
Покажем, что радиус сходимости при дифференцировании и интегрировании не меняется. Обозначим радиус сходимости данного степенного ряда через
, где
. Рассмотрим ряд, членами которого являются производные от членов данного ряда, т.е. ряд, полученный почленным дифференцированием:
. Общий член этого ряда
запишем в виде
, где
, а
— коэффициент исходного ряда. Радиус сходимости полученного ряда определим по формуле Коши-Адамара, т.е.
, где
Следовательно, . Здесь использован известный предел
, частный случай которого
был использован при решении примера 3.3. Так как ряд
получается из ряда
интегрированием, то из доказанного следует, что при интегрировании ряда радиус сходимости не изменяется.
Пример 3.11. Найти суммы следующих рядов с комплексными членами:
а) ; б)
; в)
; г)
.
Решение
Действия над степенными рядами
Кроме упомянутых выше свойств дифференцирования и интегрирования степенных рядов внутри круга сходимости как рядов, равномерно сходящихся, они обладают в круге сходимости общими свойствами сходящихся, в частности абсолютно сходящихся, рядов: ряды можно складывать и перемножать, т.е. рассматривать сумму и произведение рядов; можно также рассматривать их отношение — деление рядов.
Рассмотрим подробнее арифметические действия над степенными рядами. Обозначим и
— радиусы сходимости двух рядов
и
.
1. В общей области сходимости, т.е. в круге , где
, можно рассматривать сумму (разность) рядов: ряд
. Радиус сходимости полученного ряда не меньше
. Сумма
нового ряда равна
, где
и
— суммы рядов — слагаемых.
2. В круге можно рассматривать произведение рядов:
Получаем ряд , где
. или
. Радиус сходимости полученного ряда не меньше
, его сумма
равна
, где
n
— суммы рядов — сомножителей.
3. В некоторой окрестности точки можно рассматривать отношение рядов
(делимое) и
(делитель) при условии
. Частным этих рядов будет ряд
, такой, что выполняется равенство
Коэффициенты
определяются, как и в случае многочленов, методом неопределенных коэффициентов или делением “углом”.
Замечание 3.2. При сложении и умножении рядов, как отмечено выше, может получиться ряд, сходящийся в большей области, чем общая часть кругов сходимости двух исходных рядов: .
Приведем пример, подтверждающий это свойство. При сложении рядов и
, для которых, как нетрудно проверить, имеем
, получим ряд
. Радиус сходимости этого ряда
.
Рассмотренные арифметические операции- над рядами используются при решения задач разложения функции в степенные ряды: функций вида
Подстановка ряда в ряд
4. Еще одно действие — подстановка ряда в ряд связано с разложением в ряд сложной функции. Пусть ряд сходится в круге
, его сумма равна
; а ряд
в круге
и его сумма в этом круге равна
. Тогда в некоторой окрестности точки
, т.е. в круге
, можно рассматривать ряд
. Заметим, что для возможности выполнения этого действия требуется, чтобы имело место условие
, то есть
,в противном случае, как правило, не удается привести подобные члены. Поэтому записываем ряд в виде
Произведя действия возведения в степень (как умножение ряда на ряд) и приведение подобных членов, можно записать любое число членов ряда:
Суммой нового ряда будет функция .
Обобщение свойств степенных рядов
Обобщим свойства степенных рядов и действия над ними в виде утверждения.
Утверждение 3.1
1. Степенной ряд сходится в круге
; ряд
сходится в круге
.
2. Радиус сходимости ряда определяется по формулам (3.11) и (3.12).
3. На границах круга сходимости могут быть как точки сходимости, так и точки расходимости ряда.
4. Внутри круга сходимости ряд сходится равномерно; для ряда (3.10) это круг , для (3.9):
, где
— любое число,
.
5. Сумма степенного ряда внутри круга сходимости — функция аналитическая.
6. Внутри круга сходимости ряд можно интегрировать почленно и дифференцировать почленно любое число раз. Радиус сходимости ряда при этом не меняется. Сходимость в отдельных точках границы может измениться.
Ряды с комплексными членами по целым степеням
Рассмотрим два ряда и
. Первый ряд — степенной и, если он сходится не только в одной точке
, но и не всюду, то сходится в круге
. Второй ряд — не степенной, но, после замены
, получим степенной ряд
, область сходимости которого:
. Поэтому для ряда
имеем
, или
.
Если , то исходные ряды имеют общую область сходимости — кольцо
. Для каждого
, принадлежащего этому кольцу, получаем два сходящихся числовых ряда, которые, по свойству сходящихся числовых рядов, можно складывать. Следовательно, в области
можно рассматривать ряд вида
(3.14)
Ряд (3.14) — ряд по целым степеням, он состоит из двух частей: первое слагаемое составляют члены ряда с положительными степенями; второе слагаемое
— с отрицательными. Вторую часть можно записать в виде
, после чего становится понятней возможность записи суммы двух рядов в виде одного ряда, а именно по формуле (3.14), где полагаем
для
и
для
.
Используя для составляющих ряда (3.14) — рядов и
свойства степенных рядов (см. утверждение 3.1), можно сформулировать следующее утверждение для рядов по целым степеням.
Утверждение 3.2
1. Ряд сходится в кольце
.
2. В кольце , где
, ряд сходится равномерно.
3. В кольце сумма ряда (3.14) — функция аналитическая и ряд можно почленно интегрировать и дифференцировать любое число раз.
Пример 3.12. Найти кольцо сходимости и сумму ряда .
Решение
Запишем ряд в виде и, повторяя решение примера 3.4, находим кольцо сходимости ряда
. Сумму ряда
можно записать в виде
, где
-сумма ряда
,
— ряда
. Для нахождения суммы этих рядов применим формулу суммы членов бесконечно убывающей геометрической прогрессии. Получаем
для
и
для
. Окончательный ответ:
Заметим, что функция является аналитической всюду, кроме точек
и
, суммой данного ряда она является только в кольце
.
Отметим также, что в данном ряде отсутствует свободный член. Ряд , где свободный член равен 1 (при
), очевидно, сходится в том же кольце, а сумма его равна
Она действительно отличается только на величину свободного члена, т.е. на единицу от найденной выше.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.