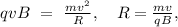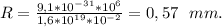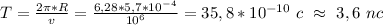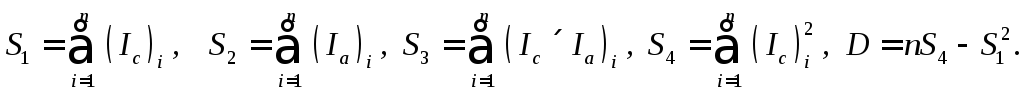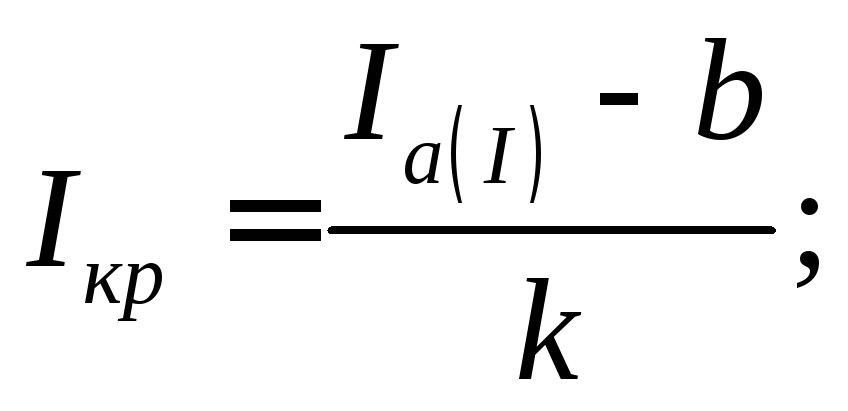Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
[ е = – 1.602 cdot 10^{-19} enspace Кл. ]
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
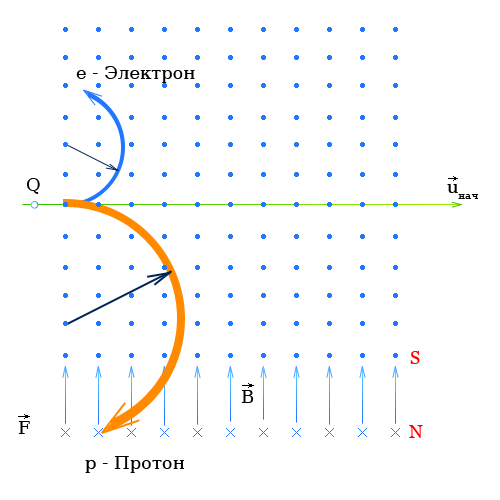
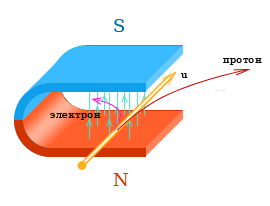
Сила Лоренца действующая на электрон и протон
Величина и направление силы Лоренца определяются соотношением
[ vector{F_{L}}= e vector{v} × vector{B} ]
где $vector{v}$, $vector{B}$ и $vector{F}$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
[ F_{L} = e v B ]
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины.
Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
Если
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10-31 кг — масса электрона, | кг |
| e | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
[ evB = frac{m_{e} v^{2}}{r} ]
и, следовательно,
[ r = frac{m_{e} v}{eB} ]
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
[ p = + 1.602 cdot 10^{-19} enspace Кл. ]
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Сила Лоренца действующая на протон
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
Если
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10-27 кг — масса протона, | кг |
| p | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
[ r = frac{m_{p} v}{p B} ]
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Сила Лоренца |
стр. 667 |
|---|
Как найти радиус окружности движения электрона
Электрон, ускоренный разностью потенциалов U = 1 кВ, влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Индукция магнитного поля В = 1,19 мкТл. Найти радиус R окружности, по которой движется электрон.
Дано:
U = 1 кВ = 10 3 В
В = 1,19 мкТл = 1,19 ·10 -6 Тл
Решение:
На электрон, движущейся в магнитном поле
действует сила Лоренца
,
которая является центростремительной
Т. к. движение электрона происходит по окружности, то
Радиус R окружности, по которой движется электрон, будет равен
Скорость электрона найдем из закона сохранения энергии
Ответ:
Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Величина и направление силы Лоренца определяются соотношением
где $vector$, $vector$ и $vector$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10 -31 кг — масса электрона, | кг |
| e | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
При больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя электронов me, а необходимо учитывать релятивистское увеличение массы.
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10 -27 кг — масса протона, | кг |
| p | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Аналогично при больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя протонов mp, а необходимо учитывать релятивистское увеличение массы.
Определите радиус окружности и период обращения электрона. Физика, 11 класс, параграф 1-7, 4 задача. Мякишев и Буховцев
Всем привет. Решили уже?
Определите радиус окружности и период обращения электрона в однородном магнитном поле с индукцией B =0,01 Тл. Скорость электрона перпендикулярна вектору магнитной индукции и равна 106 м/с.
Привет! Вот
Сила Лоренца является центростремительной силой:
Период обращения:
Ответ: 0,57 мм; 3,6 нс.
[spoiler title=”источники:”]
http://www.fxyz.ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5/%D1%8D%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%BE/%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D0%BE%D0%BB%D0%B5/%D1%81%D0%B8%D0%BB%D1%8B_%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D1%83%D1%8E%D1%89%D0%B8%D0%B5_%D0%B2_%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%BC_%D0%BF%D0%BE%D0%BB%D0%B5/%D1%81%D0%B8%D0%BB%D0%B0_%D0%BB%D0%BE%D1%80%D0%B5%D0%BD%D1%86%D0%B0/
http://class.rambler.ru/temy-gdz/opredelite-radius-okruzhnosti-i-period-obrascheniya-elektrona-fizika-11-klass-paragraf-1-7-4-zadacha-myakishev-i-buhovcev-14553.htm
[/spoiler]
Решение.
Рассмотрим движение электрона в плоском горизонтальном конденсаторе, определим скорость электрона при вылете из конденсатора. Покажем рисунок . Скорость определим по формуле:
[ vec{upsilon }={{vec{upsilon }}_{0}}+{{vec{upsilon }}_{y}},upsilon =sqrt{upsilon _{0}^{2}+upsilon _{y}^{2}}(1). ]
Со стороны пластин на электрон действует сила Кулона.
[ begin{align}
& {{F}_{K}}=ecdot E(2),{{F}_{K}}=mcdot a(3),a=frac{{{upsilon }_{y}}}{t}(4),t=frac{l}{{{upsilon }_{0}}}(5),ecdot E=mcdot a, \
& ecdot E=mcdot frac{{{upsilon }_{y}}cdot {{upsilon }_{0}}}{l},{{upsilon }_{y}}=frac{ecdot Ecdot l}{mcdot {{upsilon }_{0}}}(6).upsilon =sqrt{upsilon _{0}^{2}+{{(frac{ecdot Ecdot l}{mcdot {{upsilon }_{0}}})}^{2}}}(7). \
& upsilon =sqrt{{{({{10}^{7}})}^{2}}+{{(frac{1,6cdot {{10}^{-19}}cdot {{10}^{4}}cdot 5cdot {{10}^{-2}}}{9,1cdot {{10}^{-31}}cdot {{10}^{7}}})}^{2}}}=1,33cdot {{10}^{7}}. \
end{align}
]
Определим угол α под которым электрон вылетает из электрического поля и влетает в магнитное поле.
[ frac{{{upsilon }_{0}}}{upsilon }=sin alpha ,sin alpha =frac{{{10}^{7}}}{1,33cdot {{10}^{7}}}=0,7519.
]
Где: е – модуль заряда электрона, е = 1,6∙10-19 Кл, m – масса электрона, m = 9,1∙10-31 кг, В – индукция магнитного поля. При вылете из конденсатора электрон попадает в магнитное поле, силовые линии которого перпендикулярны силовым линиям электрического поля.
На заряженную частицу действует сила Лоренца, и сила Лоренца является центростремительной силой, выразим скорость частицы относительно оси Ох.
[ begin{align}
& {{F}_{L}}=qcdot Bcdot {{upsilon }_{x}}, {{F}_{L}}=mcdot a, a=frac{upsilon _{x}^{2}}{R},qcdot Bcdot upsilon =mcdot frac{upsilon _{x}^{2}}{R}, \
& {{upsilon }_{x}}=frac{qcdot Bcdot R}{m} (1),{{upsilon }_{x}}=upsilon cdot sin alpha ,R=frac{upsilon cdot sin alpha cdot m}{qcdot B}, \
& R=frac{1,33cdot {{10}^{7}}cdot 0,7519cdot 9,1cdot {{10}^{-31}}}{1,6cdot {{10}^{-19}}cdot {{10}^{-2}}}=5,67cdot {{10}^{-3}}. \
end{align} ]
Из этих формул также получаем формулу для расчета времени одного оборота:
[ R=frac{mcdot {{upsilon }_{x}}}{qcdot B}, T=frac{2cdot pi cdot R}{{{upsilon }_{x}}}, T=frac{2cdot pi cdot m}{qcdot B} (4). ]
Вдоль силовых линий поля магнитная сила не действует, поэтому частица движется прямолинейно с постоянной скоростью.
[ begin{align}
& {{upsilon }_{Y}}=frac{h}{T}, {{upsilon }_{Y}}=frac{hcdot qcdot B}{2cdot pi cdot m} ,{{upsilon }_{Y}}=upsilon cdot cos alpha ,cos alpha =sqrt{1-{{sin }^{2}}alpha }, \
& upsilon cdot sqrt{1-{{sin }^{2}}alpha } = frac{hcdot qcdot B}{2cdot pi cdot m},,h=frac{2cdot pi cdot mcdot upsilon cdot sqrt{1-{{sin }^{2}}alpha }}{qcdot B}. \
& h=frac{2cdot 3,14cdot 9,1cdot {{10}^{-31}}cdot 1,33cdot {{10}^{7}}cdot sqrt{1-{{(0,7519)}^{2}}}}{1,6cdot {{10}^{-19}}cdot {{10}^{-2}}}=31,32cdot {{10}^{-3}}. \
end{align}
]
Ответ: R = 6,67∙10-3 м, h = 31,32∙10-3 м.
14
Федеральное
Агентство по образованию
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И
РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики
ОТЧЕТ
Лабораторная
работа по курсу “Общая физика”
ИЗУЧЕНИЕ МАГНИТНОГО
ПОЛЯ КРУГОВОГО ТОКА
Преподаватель Студент
группы з-368-а
___________ /____________.
/ Смирнов
А.Н. /
____________ /
___________200_
г. __________ 2009г.
2009
1. ЦЕЛЬ РАБОТЫ
Целью
настоящей работы является определение
величины удельного заряда электрона
методом магнетрона.
2. ОПИСАНИЕ УСТАНОВКИ
И МЕТОДИКИ ЭКСПЕРИМЕНТА
В качестве магнетрона
используется электронная лампа 3Ц22С,
которая имеет цилиндрические анод и
катод. Диаметр катода равен 1 мм.
Несоосность между осями катода и анода
порядка 1 мм. Поэтому для данной лампы
расстояние от катода до анода можно
принять R
= (8 ± 1) мм.
На лампу надевается
соленоид с большим числом витков на
единицу длины. Густота намотки соленоида
для разных блоков (вариантов) приведена
в Журнале измерений.
Погрешность густоты
намотки соленоида составляет 5 вит./см.
Для определения
зависимости анодного тока от тока
соленоида используется следующая схема
измерения (рис. 2.1).
Рисунок 2.1 – Схема
экспериментальной установки
Значение анодного
тока измеряется микроамперметром (μA),
который вмонтирован в основную панель
лабораторного макета. Значение тока
соленоида измеряется миллиамперметром
(mA),
который также вмонтирован в основную
панель. Регулировка тока соленоида
осуществляется с помощью ручки
потенциометра RP1,
выведенную на основную панель. Ручка
потенциометра RP2
для регулирования анодного напряжения
выведена на малую панель (блок питания
лабораторного макета). В эту же панель
вмонтирован вольтметр (V),
измеряющий анодное напряжение.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ
ФОРМУЛЫ.
Значение
удельного заряда электрона вычисляется
в данной работе по формуле:
(3.1)
где:
Ua
–
анодное напряжение лампы;
μ
– относительная магнитная проницаемость
среды (для вакуума μ
= 1);
μ0
–
магнитная постоянная (в СИ
μ0
= 4·π·10-7
Гн/м);
n –
число витков, приходящихся на единицу
длины соленоида
(n
= 31500 вит/м
по условиям эксперимента ) ;
Iкр
– значение
силы тока в соленоиде, при котором
индукция магнитного
поля достигает
критического значения;
R
– расстояние от катода до анода.
Абсолютная суммарная
погрешность определения
значения
удельного заряда электрона e/m:

А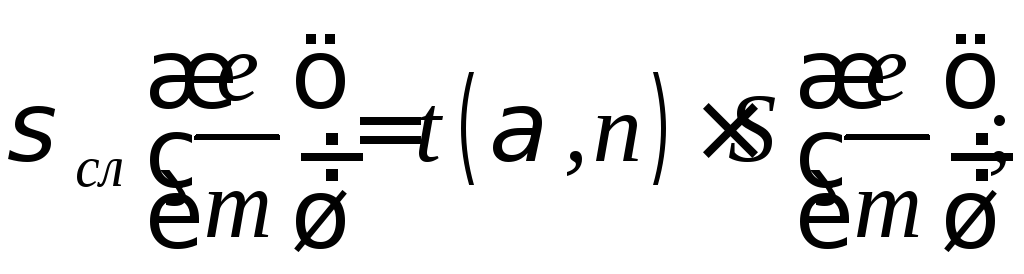
случайная погрешность
определения
удельного
заряда электрона:
(3.3)
где t(,
n)
– коэффициент
Стьюдента
с
абсолютная погрешность
определения
удельного
заряда электрона:
(3.4)
где
– значение
удельного заряда электрона при i
–ом
измерении ( i
=1. … , n),
n
– число измерений,
–среднее
значение
удельного заряда электрона.
А
систематическая погрешностьопределения
удельного
заряда электрона:
(3.5)
Относительная
систематическая погрешность определения
удельного
заряда электрона (из выражения 3.1):
(3.6)
Относительная
погрешность измерения
анодного напряжения Ua:
(3.7)
где
Δ(Ua)
–
абсолютная приборная систематическая
погрешность измерения величины Ua,
равна 1 в младшем разряде цифрового
вольтметра:
Δ(Ua)
= 0,01 В
(3.7а)
Относительная
погрешностьизмерения
расстояния от катода до анода R:
(3.8)
где Δ(R)
–
абсолютная погрешность измерения
величины R,
величина заданная:
R
= (8 ± 1) мм ; Δ(R)
= 1 мм. (3.8а)
Значение Iкр
на графике
Iа
= f(Ic)
определяется как абсцисса точки
пересечения прямых Iа(1)
= const
–горизонтальная
область 1 и Iа(2)
= kIc
+b
–
линейный участок в области 2 спада
анодного тока.
Параметры линейной
зависимости k
и b,
определяются методом наименьших
квадратов (МНК):
(3.9)
где обозначено:
(3.10)
В этих формулах n
– число экспериментальных точек, а
наборы чисел (Ic)
и (Iа)
– результаты измерений, то есть абсциссы
и ординаты экспериментальных
точек.
Погрешности
косвенного измерения параметров прямой
линии k
и b МНК
определяются по следующим формулам:
(3.11)
где
Значение Iкр
определяется
из уравнения:
Iа(1)
= k
Iкр
+b
(3.13)
получаем:
(3.14)
Относительная
погрешность определения
величины Iкр:
(3.15)
где относительные
погрешности параметров k
и b
определяются
как:
(3.16)
в выражении 3.15
погрешность величины Iа(I)
не учитывается,
как величина более малого порядка.
Относительная
погрешность густоты
намотки соленоида n:
(3.17)
где Δ(n)
–
абсолютная погрешность измерения
величины n.
Среднее
значение
удельного заряда электрона:
(3.18)
4. РЕЗУЛЬТАТЫ РАБОТЫ
И ИХ АНАЛИЗ.
Измеренные значения
и результаты их обработки приведены в
таблице.
Таблица 4.1
Зависимость
анодного тока Iа
от тока
соленоида Iс
при
различных значениях анодного напряжения
Uа
|
№№ опыта |
Uа |
Uа |
Uа |
Uа |
||||
|
Iс, mA |
Iа, μA |
Iс, mA |
Iа, μA |
Iс, mA |
Iа, μA |
Iс, mA |
Iа, μA |
|
|
1 |
50,23 |
200,00 |
49,982 |
200,00 |
49,843 |
200,00 |
76,075 |
200,00 |
|
2 |
61,10 |
143,60 |
68,386 |
154,40 |
74,376 |
178,00 |
80,139 |
191,60 |
|
3 |
61,32 |
120,00 |
68,297 |
162,80 |
74,682 |
152,00 |
80,240 |
186,40 |
|
4 |
60,705 |
180,00 |
68,995 |
103,60 |
74,877 |
137,20 |
80,509 |
166,00 |
|
5 |
61,239 |
130,00 |
69,037 |
101,20 |
75,194 |
111,20 |
80,675 |
152,00 |
|
6 |
60,763 |
174,40 |
68,839 |
116,80 |
74,843 |
140,40 |
80,935 |
137,20 |
|
7 |
61,201 |
132,40 |
68,877 |
111,20 |
74,948 |
130,00 |
80,951 |
137,20 |
|
8 |
61,803 |
79,20 |
69,221 |
82,40 |
75,454 |
91,60 |
81,059 |
122,80 |
|
9 |
61,611 |
94,00 |
69,114 |
94,00 |
76,075 |
49,60 |
81,253 |
111,20 |
|
Iкр |
Iкр |
Iкр |
Iкр |
На основании
экспериментальных данных (табл.4.1)
строятся графики зависимости анодного
тока от тока соленоида для различных
значений анодного напряжения (рис.4.2).
Определение
зависимости анодного тока от тока
соленоида.
Значение анодного
тока соответствующее горизонтальной
части кривых графика:
Ia(I)=
200 mA
Для линейных
участков кривых зависимость описывается
уравнением:
Iа
= k∙Ic
+ b
Графики зависимости
анодного тока от тока соленоида для
различных значений анодного напряжения
(рис.4.2).
Расчет параметров
линейной зависимости:
Зависимость
анодного тока от тока соленоида.
Таблица 4.3.
|
Uа, |
n |
параметр |
параметр |
Зависимость Iа |
Iкр 10-3A |
ε(Iкр)% |
σ(Iкр) 10-3A |
||||
|
k∙10-3 |
σ(k)∙10-3 |
ε(k)% |
b∙10-3A |
σ(b) ∙10-3A |
ε(b)% |
||||||
|
8,02 |
8 |
-2,1 |
1,26 |
0,6 |
131,6 |
2,28 |
0,02 |
− (2,1∙Ic |
61,2 |
0,6 |
0,4 |
|
10,09 |
8 |
-1,7 |
1 |
0,6 |
115,8 |
2,1 |
0,02 |
− (1,7∙Ic |
68,8 |
0,6 |
0,4 |
|
12,02 |
8 |
-1,6 |
1 |
0,6 |
123,6 |
2,3 |
0,02 |
− (1,6∙Ic |
75,5 |
0,6 |
0,4 |
|
14,04 |
8 |
-1,9 |
1,1 |
0,6 |
150,6 |
2,8 |
0,02 |
− (1,9∙Ic |
80,7 |
0,6 |
0,5 |
Удельный заряд
электрона при Uа
= 8,02 В (3.1):
Погрешности
экспериментальной установки:
Относительная
погрешностьизмерения
расстояния от катода до анода R
(3.8, 3.8а):
Относительная
погрешность густоты
намотки соленоида n
(3.17):
Относительная
погрешность измерения
анодного напряжения Ua
(3.7, 3.7а):
Относительная
систематическая погрешность определения
удельного
заряда электрона (3.6):
Абсолютная
систематическая погрешность определения
удельного
заряда электрона:
Аналогично
выполняется расчет для других значениях
Ua.
Результаты расчетов
представлены в таблице 4.4.
Систематическая
погрешность определения
удельного
заряда
электрона. Таблица
4.4.
-
Uа,
В(e/m)×1011
Кл/кгε(Uа),%
ε(n),%
ε(Iкр),%
ε(R),%
%
×1011
Кл/кг8,02
1,710
0,12
1,59
0,6
12,5
25,2
0,430
10,09
1,702
0,1
0,6
25,2
0,429
12,02
1,684
0,08
0,6
25,2
0,424
14,04
1,722
0,07
0,6
25,2
0,434
∑
6,818
1,717
Среднее значение
удельного заряда электрона (3.18):
Среднее значение
абсолютной систематической погрешности
определения удельного заряда электрона
:
Стандартная
абсолютная погрешность определения
удельного
заряда электрона (3.4):
Абсолютная случайная
погрешность определения удельного
заряда электрона (3.3), коэффициент
Стьюдента
t(0,9;
4) = 2,4:
Абсолютная суммарная
погрешность определения
значения
удельного заряда электрона e/m
(3.2):
Окончательный
результат:
Относительная
погрешность определения
значения
удельного заряда электрона e/m:
5. ВЫВОДЫ
В ходе выполнения
лабораторной работы изучена работа
магнетрона, сняты зависимости анодного
тока в лампе от тока соленоида при
различных значениях анодного напряжения
Uа.
По полученным
значениям на одном графике были построены
четыре зависимости Iа
= f(Iс)
и определены значения критического
тока Iкр.
Вид полученных
кривых соответствует теоретическому
виду.
На основании
полученных значений критического тока
Iкррассчитан удельный
заряд электрона и сделана оценка
погрешности:
табличное значение:
о
от табличного значения:
– экспериментально
подтверждена справедливость формулы:
Лампа магнетрона
имеет несоосность между осями катода
и анода порядка 1 мм и ε(R)
= 12,5%. Величина этой погрешности очень
большая, что и дает в итоге большую
погрешность эксперимента:
6. ОТВЕТЫ НА
КОНТРОЛЬНЫЕ ВОПРОСЫ
В магнетронной
системе поток заряженных частиц
управляется одновременно электрическим
и магнитным полями, направленными
взаимно перпендикулярно. В качестве
магнетрона можно использовать электронную
лампу с цилиндрическим анодом и
прямолинейным катодом, расположенным
на оси анода. Между анодом и катодом
приложено постоянное напряжение,
создающее радиальное электрическое
поле. На лампу надевают соленоид, по
которому протекает постоянный ток,
создающий постоянное магнитное поле,
направленное вдоль оси анода (рис. 5.1).
1
– катод;
2
– анод;
3 –
соленоид.
Рисунок
5.1 – Магнетрон
В качестве магнетрона
используется электронная лампа 3Ц22С,
которая имеет цилиндрические анод и
катод. На лампу надевается соленоид с
большим числом витков на единицу длины.
2.От чего зависит радиус кривизны траектории электрона в магнетроне?
Под
действием магнитного поля магнетрона
траектория движения электрона станет
криволинейной.
Из уравнения
следует,
что радиус кривизны траектории зависит
от скорости
электрона и от
величины магнитной индукции поля
соленоида:
3. Какая сила называется силой Лоренца и как определяется её направление?
На заряд, движущийся
в магнитном поле действует сила Лоренца:
FЛ
= e[v,B],
где e
– заряд электрона;
v
– скорость электрона;
B
– индукция магнитного поля.
Направление вектора
индукции магнитного поля В
определяется
по правилу буравчика. Направление силы
Лоренца определяется по правилу
в
произведения с учётом знака заряда.
Вектор силы всегда перпендикулярен
вектору скорости электрона.
Магнитная
сила, действующая на движущийся
положительный заряд, направлена
перпендикулярно к плоскости векторов
v и В в ту сторону, в которую поступательно
перемещается правый винт, если его
поворачивать по кратчайшему расстоянию
от вектора v
Рисунок 5.2 к вектору
В (рис. 5.2).
4. Почему сила Лоренца не изменяет кинетической энергии заряженной частицы?
Свойством силы
Лоренца является то, что ее работа всегда
равна нулю. Это следует из того, что
магнитная сила перпендикулярна к
скорости частицы. Элементарное перемещение
движущейся частицы направлено вдоль
скорости. Следовательно, скалярное
произведение силы на перемещение частицы
(элементарная работа) равно нулю. Таким
образом, магнитное поле в отличие от
электрического не в состоянии
непосредственно передать энергию
заряженной частице.
Учитывая, что
магнитное поле не совершает работы над
заряженной частицей, ее кинетическая
энергия остается постоянной (остается
постоянным модуль скорости частицы).
Магнитное поле способно изменять только
направление движения частицы. Поэтому
нормальное ускорение отлично от нуля.
5. По какому правилу и как определяется направление вектора магнитной индукции в соленоиде при заданном направлении тока в нём?
Внутри длинного
соленоида с током магнитное поле является
однородным и линии магнитной индукции
параллельны между собой. Направление
В и направление тока в витках соленоида
связаны правилом правого винта (рис.
5.3).
Рисунок
5.3.
Правило правого
винта: если
поместить острие винта в центре витка
и вращать винт в направлении тока, то
его поступательное движение укажет
направление линий магнитной индукции.
Таким
образом, существует взаимная связь
направлений тока в замкнутом проводнике
и его магнитного поля, их «сцепленность».
Соседние файлы в папке Физика ЛР№4 ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ КРУГОВОГО ТОКА
- #
22.06.201413.49 Кб16phyLab4.reg
- #
22.06.20146.67 Кб15журнал ЛР№4.txt
- #
- #
Помогите по физике!!! Пожалуйста!!!!
Екатерина Колесова
Знаток
(454),
закрыт
11 лет назад
Электрон, имеющий скорость 4,8 ּ 107 м/с, влетает в вертикальное магнитное поле перпендикулярно линиям индукции. Определите радиус окружности, по которому движется электрон в поле индукции 85 мТл.
Анатолий Ушаков
Мыслитель
(6194)
12 лет назад
Дано:
скорость электрона
V=4,8ּ10^7 м/с
индукция магнитного поля
B=85 мТл = 0,085Тл
Найти радиус окружности, по которому движется электрон
r -?
масса электрона
me=9.11ּ10^-31
заряд электрона
qe=1.6ּ10^-19
Формула: r = ( me * V ) / ( qe * B )
r = ( 9.11*10^-31 * 4.8*10^7 ) / ( 1.6*10^-19 * 0.085 ) = 9.91*10^-4 м
Ответ: r = 9.91*10^-4 м или 9.9 см