Математика, 3 класс
Урок №33. Круг. Окружность (центр, радиус, диаметр)
Перечень вопросов, рассматриваемых в теме:
– что такое окружность и круг?
– какие элементы имеет окружность?
– чем отличается круг от окружности?
Глоссарий по теме:
Окружность – это замкнутая кривая, все точки которой одинаково удалены от центра.
Круг – это геометрическая фигура, которая ограничена окружностью.
Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности.
Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. с. 94-96.
2. Рудницкая В. Н. Тесты по тматематике:3 класс. М.:Издательство «Экзамен», 2016 с. 48-51.
3. Рудницкая В.Н. Контрольные работы по математике:3 класс. М.: Издательство»Экзамен», 2017, с. 49-54.
4. Рудницкая В. Н. КИМ ВПР. Математика .3 класс. М.: Издательство «Экзамен», 2018, с. 77-79.
Теоретический материал для самостоятельного изучения
С незапамятных времен люди используют в своей жизни круг.
1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).
2. Мы не можем представить свою жизнь без машин: автобус, велосипед, швейная, машинки, самолет, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес.
3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир .
5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль.
6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду.
Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.
Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.
Круг – символ цикличности, повторяемости. Все движется по кругу.
Круг дает ощущение взаимосвязи с Космосом.
Сама природа выбирает эту удобную и компактную форму как шар и круг.
Сравним две фигуры.
На 1 рисунке видим замкнутую кривую линию, на которой находятся точки К и С на одинаковых расстояниях от точки О.Такая замкнутая кривая называется окружностью. Точка О – центр окружности. Все точки, поставленные на окружности, находятся на одинаковом расстоянии от центра!

Есть специальный инструмент, который позволяет чертить окружности – это циркуль.

На рисунке 2 видим геометрическую фигуру, которая ограничена окружностью. Эта фигура называется круг.
Вывод: окружность – граница круга; круг – часть внутри окружности. В таблице указаны отличительные признаки круга и окружности:

Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом.
Если соединить 2 точки окружности, проходящих через центр, получится отрезок, который называется диаметром.
Диаметр делит круг на две равные части и все диаметры у окружности равной длины.


Задания тренировочного модуля:
1. Длина радиуса составляет 6 см. Чему равен диаметр окружности?
6см; 12 см; 3см.
Правильный ответ: 12см.
2. Заполните таблицу
|
радиус |
4 см |
3 см |
7 дм |
5 дм |
|
диаметр |
Правильный ответ:
|
радиус |
4 см |
3 см |
7 дм |
5 дм |
|
диаметр |
8 см |
6 см |
14 дм |
10 дм |
Математика. 3 класс
Конспект урока
Математика, 3 класс
Урок №33. Круг. Окружность (центр, радиус, диаметр)
Перечень вопросов, рассматриваемых в теме:
– что такое окружность и круг?
– какие элементы имеет окружность?
– чем отличается круг от окружности?
Глоссарий по теме:
Окружность – это замкнутая кривая, все точки которой одинаково удалены от центра.
Круг – это геометрическая фигура, которая ограничена окружностью.
Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности.
Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. с. 94-96.
2. Рудницкая В. Н. Тесты по тматематике:3 класс. М.:Издательство «Экзамен», 2016 с. 48-51.
3. Рудницкая В.Н. Контрольные работы по математике:3 класс. М.: Издательство»Экзамен», 2017, с. 49-54.
4. Рудницкая В. Н. КИМ ВПР. Математика .3 класс. М.: Издательство «Экзамен», 2018, с. 77-79.
Теоретический материал для самостоятельного изучения
С незапамятных времен люди используют в своей жизни круг.
1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).
2. Мы не можем представить свою жизнь без машин: автобус, велосипед, швейная, машинки, самолет, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес.
3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир .
5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль.
6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду.
Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.
Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.
Круг – символ цикличности, повторяемости. Все движется по кругу.
Круг дает ощущение взаимосвязи с Космосом.
Сама природа выбирает эту удобную и компактную форму как шар и круг.
Сравним две фигуры.
На 1 рисунке видим замкнутую кривую линию, на которой находятся точки К и С на одинаковых расстояниях от точки О.Такая замкнутая кривая называется окружностью. Точка О – центр окружности. Все точки, поставленные на окружности, находятся на одинаковом расстоянии от центра!
Есть специальный инструмент, который позволяет чертить окружности – это циркуль.
На рисунке 2 видим геометрическую фигуру, которая ограничена окружностью. Эта фигура называется круг.
Вывод: окружность – граница круга; круг – часть внутри окружности. В таблице указаны отличительные признаки круга и окружности:
Если соединить любую точку окружности с ее центром, то получится отрезок, который называется радиусом.
Если соединить 2 точки окружности, проходящих через центр, получится отрезок, который называется диаметром.
Диаметр делит круг на две равные части и все диаметры у окружности равной длины.
Задания тренировочного модуля:
1. Длина радиуса составляет 6 см. Чему равен диаметр окружности?
Круг. Окружность (центр, радиус, диаметр)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
Нахождение радиуса круга: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса круга
1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:
C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2 π R
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:
S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:
S = π R 2
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
[spoiler title=”источники:”]
http://interneturok.ru/lesson/matematika/3-klass/tema-umnozhenie-i-delenie/krug-okruzhnost-tsentr-radius-diametr
[/spoiler]
Задачи урока:
- Познакомить с определением радиуса окружности, научить находить радиусы на рисунках, чертить их.
- Развивать логическое мышление и познавательную активность в процессе исследовательской деятельности, эмоциональную сферу, речь.
- Формировать умение общаться, работать в группах, самооценку.
Оборудование:
- Аргинская И.И., Ивановская Е.И. Математика: Учебник для 3кл., Самара: Корпорация “Федоров”; Изд. “Учебная литература”, 2006.
- Карточки с окружностями. Карточки для индивидуальной работы. (Приложение 1)
- Циркули, карандаши, линейки.
Ход урока
I. Организационный момент.
Прозвенел уже звонок,
Сядьте тихо и неслышно,
И скорей начнём урок.
Будем мы писать, трудиться,
Ведь заданья нелегки.
Нам, друзья, нельзя лениться,
Так как мы ученики.
II. Устный счет.
1. Индивидуальная работа (задание на карточках)
|
234 + 543 = … 873 – 652 = … |
… + 435 = 768 657 – … = 124 |
632 + … = 844 … – 341 = 652 |
2. “Головоломка”
– Назови следующие три числа, объясни правило, по которому составлен ряд чисел.
1) 2, 4, 7, 11, 16, 22, … (29, 37, 46)
2) 10, 8, 11, 9, 12, 10, 13, …(11, 14, 12)
3. Выразите:
| 2 дм 3 см =….см
2 м 4 дм =…см |
4 ц=….кг 7 ц=….кг |
4. Блиц-турнир. “Какое слово лишнее?”
– Почему?
a) Математика, русский язык, чтение, тетрадь, английский язык, физ-ра.
б) Делимое, делитель, частное, плюс.
в) Стол, стул, диван, тарелка, шкаф.
5. Задачи на смекалку
– Когда об воду можно порезать руку? (когда она превратится в лёд)
– У меня 4 сына. У каждого из них есть родная сестра. Сколько детей у меня? (5)
– Можно ли пустое ведро наполнить три раза подряд, ни разу не выливая из него? (нет)
– Установи порядок: прямоугольник, многоугольник, круг, квадрат, четырехугольник. Что “лишнее”? Почему? (круг – нет углов)
III. Закрепление ранее изученного.
Слайд (Приложение 2)
– На какие две группы можно разделить фигуры? (на круги и окружности)
– Назовите их номера? (круги – 1, 4, 6, 2, окружности – 3, 5, 7)
– Рассмотрим ваши узоры из окружностей, выполненные дома и вспомним всё то, чему научились на прошлом уроке. (3 ученика у доски)
– Как называется граница круга?
– Чем отличается окружность от круга?
– С помощью какого инструмента вы чертили окружности?
– Вспомните правила безопасной работы с циркулем.
IV. Изучение нового: исследование, наблюдение, вывод.
– Я вас просила вырезать из цветной бумаги круг, приготовьте его для работы. Теперь вместе со мной выполняем следующие действия.
– Согните круг так, чтобы центр оказался на линии сгиба. Сколько половин в круге получилось? (Две)
– Круг разделили на две части и получили две половины.
– Как вы думаете, части получились одинаковые? Равные?
– Они подходят, т.к совмещаются.
– Посмотрим на линию сгиба? Какая она? (Она прямая.)
– Верно, линия сгиба прямая. Есть ли у нее начало и конец? (Есть.)
– А как называется линия, у которой есть начало и конец? (Отрезок)
– Правильно, ребята. Молодцы. Посмотрите, я еще построю несколько отрезков в этом круге. (Учитель делает в круге еще несколько сгибов параллельно диаметру.)
– Чем же интересны эти отрезки? (Они проходят через центр)
Отрезок, который проходит от края круга до другого края через центр, называется – диаметр.
Слайд
– Из всех отрезков, соединяющих два противоположных края круга, диаметр – самый длинный.
– Так сколько диаметров можно провести в окружности? (много)
– А какие они должны быть все по длине? (одинаковые)
– Еще можно сказать равные.
– Продолжаем работу с нашим кругом .
– Согните ваш круг по диаметру. (Дети складывают.)
– Вы получили полукруг. А теперь сложите полукруг пополам.
– Где оказался центр круга? Покажите его.
– У этой фигуры, которую мы получили, есть свое название.
– Разверните ваш круг. Проведите пальцем от центра круга до его края по сгибу. Этот маленький отрезок называется, словом радиус.
– Сколько радиусов на вашем круге? (4 радиуса)
– Какие по длине все радиусы? Проверьте с помощью циркуля. (Радиусы одинаковые.)
– Чтобы дать верное определение радиуса, мы попробуем выбрать из уже предложенных их детьми. (Учебник стр.74 №140 – объяснить свой выбор)
Слайд
V. Закрепление
1. Задание.
– А теперь мы проверим ваши знания. Я предлагаю вам первое задание.
– Рассмотрите рисунок. Что на нем изображено? (окружность)
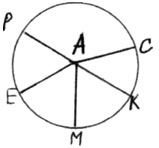
– Кто знает, как называется отрезок AM? (Радиус окружности.)
– Подумайте, есть ли здесь другие радиусы? Если есть, назовите их имена (один ученик пишет на доске ЕА, АР, АС, АК).
– Начертите свою окружность и проведите в ней несколько радиусов.
2. Задание
– Запиши имена линий, которые не являются радиусами. (СЕ, АВ, XУ, ОУ, РЛ)
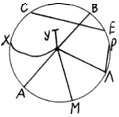
3. Задание
– Начерти окружность, проведи в ней зелёным цветом 3 радиуса, синим столько же отрезков, которые не являются радиусами.
(взаимопроверка и взаимооценка в паре).
– Оценим работу группы (+ хорошо, ошибки исправлены).
4. Задание
– А сейчас я вам предлагаю задание на закономерность Слайд
– В данных окружностях нарисованы радиусы по определённому правилу.
– Пронаблюдайте, по какому правилу нарисованы радиусы?
– Попробуйте догадаться, какой радиус я должна нарисовать в последних окружностях. Если вы внимательно посмотрите на первый ряд, то найдёте отгадку. (по часовой стрелке располагаются радиусы)
Физминутка. (Дежурный ученик проводит упражнения для снятия усталости рук, головы, глаз.)
5. Задание – самостоятельная работа
№ 142 (по рядам: 1 ст. – 1 ряд, 2ст.– 2 ряд, 3ст.– 3 ряд; 3 человека у доски).
VI. Домашнее задание.
№ 141 (1).
7. Итоги урока.
– Что нового узнали на уроке?
– С каким настроением работали?
Как найти радиус окружности
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Окружность
Приступаем к изучению окружности и круга. Вспомним замкнутые и незамкнутые линии. Познакомимся с центром окружности, радиусом и диаметром и научимся определять радиус при известном диаметре и диаметр при известном радиусе.
Окружность и овал
Для начала рассмотрим рисунок и найдём окружность:

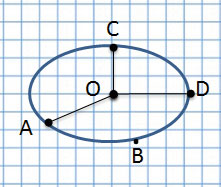
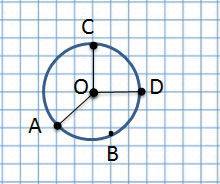
Теперь рассмотрим сходства и различия этих геометрических фигур:
| Овал | Окружность | |
|
|
 |
|
| Сходства |
Центр в точке О Есть точки A,B,C,D |
|
| Различия | В овале отрезки от точки O до крайней линии разные, а в окружности – все отрезки одинаковые. |
Правило:
Окружность – это замкнутая кривая линия с точкой О в середине, которая называется центром.
Расстояния от центра до линии окружности одинаковые.
Начертить окружность можно при помощи циркуля:
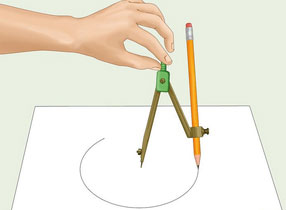
А овал рисуют от руки:

Окружность и круг
Если заполнить пространство внутри окружности, то получим круг.
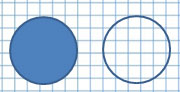
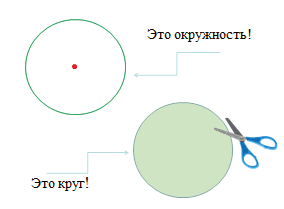
Круг – это часть плоскости, ограниченная окружностью.
Диаметр и радиус
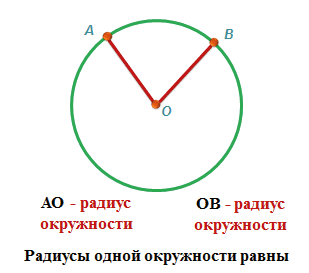
Если соединить центр окружности с линией окружности, получим радиус, например, OC, OA и OD.

Радиус – длина отрезка, соединяющего центр окружности с любой точкой, лежащей на окружности. Радиус составляет половину диаметра.
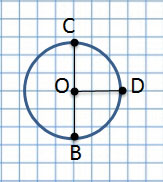
Если отрезок проходит через центр и соединяет две точки на окружности – это диаметр.
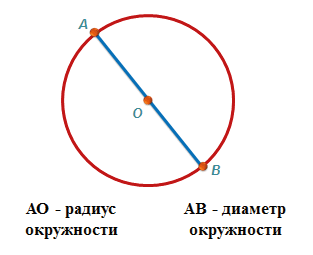
Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего две точки на этой окружности.
Советуем посмотреть:
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Площадь фигуры
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 25. Урок 9,
Петерсон, Учебник, часть 3
Страница 26. Урок 9,
Петерсон, Учебник, часть 3
Страница 30. Урок 10,
Петерсон, Учебник, часть 3
Страница 33. Урок 11,
Петерсон, Учебник, часть 3
Страница 36. Урок 12,
Петерсон, Учебник, часть 3
Страница 39. Урок 13,
Петерсон, Учебник, часть 3
Страница 63. Урок 23,
Петерсон, Учебник, часть 3
Страница 109. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 105,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 106,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38. ПР 5. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 18,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 17. Урок 7,
Петерсон, Учебник, часть 2
Страница 43. Урок 17,
Петерсон, Учебник, часть 2
Страница 65. Урок 28,
Петерсон, Учебник, часть 3
Страница 77. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 53,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 43,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 109,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2