Определение центра масс, теория и онлайн калькуляторы
Определение центра масс
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Радиус-вектор и координаты центра масс
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: ${overline{r}}_1 и {overline{r}}_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором ${overline{r}}_C$ (рис.1).
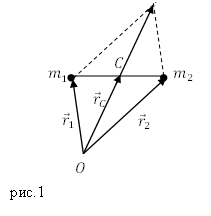
Из рис.1 видно, что:
[{overline{r}}_C=frac{{overline{r}}_1+ {overline{r}}_2}{2}left(1right).]
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен ${overline{r}}_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
[{overline{r}}_C=frac{{overline{r}}_1m_1+ {overline{r}}_2m_2}{m_1+m_2}left(2right).]
Радиус -вектор ${overline{r}}_C$, определенный выражением (2) – средне взвешенная величина радиус-векторов частиц ${overline{r}}_1$ и ${overline{r}}_2$. Это становится очевидным, если формулу (2) представить в виде:
[{overline{r}}_C=frac{m_1}{m_1+m_2}{overline{r}}_1+frac{m_2}{m_1+m_2}{overline{r}}_2left(3right).]
Выражение (3) показывает, что радиус-вектор каждой частицы входит в ${overline{r}}_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус – вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(4right).]
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(5right).]
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Скорость центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) запишем как:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(8right),]
где $overline{P}$ – суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач на определение центра масс
Пример 2
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
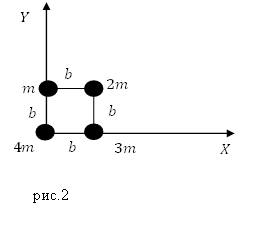
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_с=frac{sumlimits_i{Delta m_iy_i}}{m}. end{array}
right.]
Вычислим массу рассматриваемой системы точек:
[m=m+2m+3m+4m=10 m.]
Тогда абсцисса центра масс $x_{c } $равна:
[x_c=frac{0cdot 4m+3mcdot b+2mcdot b}{10m}=0,5 b.]
Ордината $y_с$:
[y_с=frac{0cdot m+mcdot b+2mcdot b}{10m}=0,3 b.]
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Пример 2
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
[frac{s_1}{s_2}=frac{m_2}{m_1}left(2.1right).]
По условию:
[s=s_1+s_2left(2.2right).]
Из уравнений (2.1) и (2.2) получаем:
[s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}.]
Ответ. $s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}$
Читать дальше: период и частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $<overline>_1 и <overline>_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $<overline>_C$ (рис.1).
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $<overline>_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
Радиус -вектор $<overline>_C$, определенный выражением (2) – средне взвешенная величина радиус-векторов частиц $<overline>_1$ и $<overline>_2$. Это становится очевидным, если формулу (2) представить в виде:
Выражение (3) показывает, что радиус-вектор каждой частицы входит в $<overline>_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус – вектор, определяющий положение центра масс находим как:
Выражение (4) считают определением центра масс системы.
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
где $overline
$ – суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач на определение центра масс
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
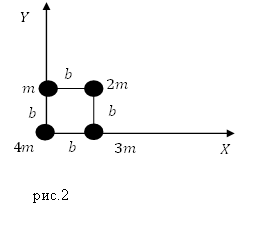
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
Вычислим массу рассматриваемой системы точек:
Тогда абсцисса центра масс $x_ $равна:
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
3.5. Центр масс
Снова рассмотрим ту же систему материальных точек. Построим радиус-вектор  по следующему правилу:
по следующему правилу:

где  — радиус-вектор
— радиус-вектор  — той материальной точки системы, а
— той материальной точки системы, а  — ее масса.
— ее масса.
Радиус-вектор  определяет положение в пространстве центра инерции (центра масс) системы.
определяет положение в пространстве центра инерции (центра масс) системы.
Вовсе не обязательно, что в центре масс системы окажется какая-то материальная точка.
Пример. Найдем центр масс системы, состоящей из двух маленьких шариков — материальных точек, соединенных невесомым стержнем (рис. 3.29). Такая система тел называется гантелей.

Рис. 3.29. Центр масс гантели
Из рис. видно, что


Подставляя в эти равенства выражение для радиус-вектора центра масс



Отсюда следует, что центр масс лежит на прямой, проходящей через центры шаров. Расстояния l1 и l2 между шарами и центром масс равны соответственно


Центр масс ближе к тому шарику, масса которого больше, что видно из отношения:

Определим, с какой скоростью движется центр инерции системы. Дифференцируем по времени обе части:

В числителе полученного выражения в правой части стоит сумма импульсов всех точек, то есть импульс  системы. В знаменателе стоит полная масса системы
системы. В знаменателе стоит полная масса системы

Мы получили, что скорость центра инерции связана с импульсом системы и ее полной массой таким же соотношением, какое справедливо для материальной точки:

Видео 3.11. Движение центра масс двух одинаковых тележек, связанных пружиной.
Таким образом, можно считать, что скорость VC является скоростью системы как целого. Она, разумеется, может отличаться от скоростей каждого из тел, входящих в систему.
Центр масс замкнутой системы движется всегда с постоянной скоростью, поскольку импульс такой системы сохраняется.
Если продифференцировать теперь выражение для импульса системы по времени и учесть, что производная импульса системы есть равнодействующая внешних сил, то получим уравнение движения центра масс системы в общем случае:

Центр масс системы движется точно так же, как двигалась бы материальная точка с массой, равной массе всех частиц системы, под действием векторной суммы всех внешних сил, приложенных к системе.
Если имеется система материальных точек, внутреннее расположение и движение которых нас не интересует, мы вправе считать ее материальной точкой с координатами радиус-вектора центра инерции и массой, равной сумме масс материальных точек системы.
Если связать с центром масс замкнутой системы материальных точек (частиц) систему отсчета (ее называют системой центра масс), то полный импульс всех частиц в такой системе окажется равным нулю. Таким образом, в системе центра масс замкнутая система частиц как целое покоится, и существует только движение частиц относительно центра масс. Поэтому ясно выявляются свойства внутренних процессов, протекающих в замкнутой системе.
В случае, когда системой является тело с непрерывным распределением масс, определение центра масс остается по существу тем же. Окружаем произвольную точку  в нашем теле небольшим объемом
в нашем теле небольшим объемом  . Масса, заключенная в этом объеме, равна
. Масса, заключенная в этом объеме, равна  , где
, где  — плотность вещества тела, которая может и не быть постоянной по его объему. Сумма по всем таким элементарным массам заменяется теперь на интеграл по всему объему
— плотность вещества тела, которая может и не быть постоянной по его объему. Сумма по всем таким элементарным массам заменяется теперь на интеграл по всему объему  тела, так что для положения центра масс тела получается выражение
тела, так что для положения центра масс тела получается выражение

Если вещество тела однородно, плотность его постоянна, и ее можно вынести из-под знака интеграла, так что она сократится в числителе и знаменателе. Тогда выражение для радиус-вектора центра масс тела принимает вид

где  — объем тела.
— объем тела.
И в случае непрерывного распределения масс справедливо утверждение, что
Центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием векторной суммы всех внешних сил,приложенных к телу.
Пример. Если снаряд взрывается в некоторой точке своей параболической траектории, то осколки летят по самым различным траекториям, но его центр масс продолжает движение по параболе.
Движение центра масс системы
Допустим, что у нас есть некоторая система, состоящая из n -ного количества материальных точек. Возьмем одну из них и обозначим ее массу как m k . Приложенные к точке внешние силы (как активные силы, так и реакции связей) имеют равнодействующую F k e . Внутренние силы имеют равнодействующую F k l . Наша система находится в движении, следовательно, нужная точка будет иметь ускорение a k . Зная основной закон динамики, мы можем записать следующую формулу:
m k a k = F k e + F k l .
Ее можно применить к любой точке системы. Значит, для всей системы целиком можно сформулировать следующие уравнения:
m 1 a 1 = F 1 e + F 1 l , m 2 a 2 = F 2 e + F 2 l , ⋯ m n a n = F n e + F n l .
Данная формула состоит из дифференциальных уравнений, описывающих движение системы в векторной форме. Если мы спроецируем эти равенства на соответствующие координатные оси, то у нас получатся дифференциальные уравнения движения в проекциях. Но в конкретных задачах чаще всего вычислять движение каждой точки системы не требуется: можно ограничиться характеристиками движения всей системы в целом.
Движение центра масс: основная теорема
Характер движения системы можно определить, зная закон, по которому движется ее центр масс.
Центр инерции системы (центр масс) – это воображаемая точка с радиус-вектором R , выражаемым через радиус-векторы r 1 , r 2 , . . . соответствующих материальных точек по формуле R = m 1 r 1 + m 2 r 2 + . . . + m n r n m .
Здесь сумма показателей в числителе m = m 1 + m 2 + . . . + m 3 выражает общую массу всей системы.
Для нахождения этого закона нам нужно взять уравнения движения системы, приведенные в предыдущем пункте, и сложить их правые и левые части. У нас получится, что:
∑ m k a k ¯ = ∑ F k ¯ e + ∑ F k ¯ l .
Взяв формулу радиус-вектора центра масс, получим следующее:
Теперь возьмем вторую производную по времени:
Здесь буквой a c ¯ обозначено ускорение, которое приобретает центр масс системы.
Свойство внутренних сил в системе гласит, что F k l равно нулю, значит, окончательное равенство будет выглядеть так:
M a c ¯ = ∑ F k ¯ e .
Это уравнение является записью закона движения центра масс. Запишем его:
Движение центра масс системы идентично движению материальной точки той же массы, что и вся система целиком, к которой приложены все действующие на систему внешние силы.
Иначе говоря, произведение ускорения центра масс системы на массу самой системы будет равно геометрической сумме всех внешних сил, действующих на эту систему.
Возьмем полученное выше уравнение и спроецируем его правую и левую части на соответствующие координатные оси. У нас получится:
M x c ¨ = ∑ F k x ¯ e , M y c ¨ = ∑ F k y ¯ e , M z c ¨ = ∑ F k z ¯ e .
Эти равенства являются дифференциальными уравнениями движения центра масс в проекции на оси в декартовой системе координат.
Практическое значение теоремы о движении центра масс
Данная теорема имеет большую практическую ценность. Поясним, в чем именно она заключается.
- Любое тело, движущееся поступательно, может быть рассмотрено в качестве материальной точки, масса которой равна массе всего тела. Во всех других случаях такой подход возможен лишь тогда, когда для определения положения тела в пространстве нам будет достаточно знать, в каком положении находится его центр масс. Также важно, чтобы условия задачи допускали исключение вращательной части движения тела.
- С помощью теоремы движения центра масс системы мы можем не рассматривать в задачах неизвестные нам заранее внутренние силы.
Разберем пример применения теоремы для решения практической задачи.
Условие: к оси центробежной машины на нити подвешено кольцо из металла. Оно совершает равномерные вращательные движения с угловой скоростью, равной ω . Вычислите, на каком расстоянии центр кольца находится от оси вращения.
Решение
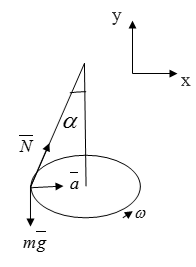
Очевидно, что система находится под воздействием силы тяжести N N ¯ α α . Также необходимо учесть силу натяжения нити и центростремительное ускорение.
Второй закон Ньютона для системы будет выглядеть так:
Теперь создадим проекции обеих частей равенства на оси абсцисс и ординат и получим:
N sin α = m a ; N cos α = m g .
Мы можем разделить одно уравнение на другое:
Поскольку a = υ 2 R , υ = ω R , то нужное нам уравнение будет выглядеть так:
[spoiler title=”источники:”]
http://online.mephi.ru/courses/physics/osnovi_mehaniki/data/lecture/3/p5.html
http://zaochnik.com/spravochnik/fizika/osnovy-dinamiki/dvizhenie-tsentra-mass-sistemy/
[/spoiler]
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июля 2022 года; проверки требуют 3 правки.
Центр масс (тж. центр ине́рции) — геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого[1]. Радиус-вектор данной точки задаётся формулой
где 
Использование понятия центра масс, а также системы координат, связанной с центром масс, удобно во многих приложениях механики и упрощает расчёты. Если на механическую систему не действуют внешние силы, то её центр масс движется с постоянной по величине и направлению скоростью.
Джованни Чева применял рассмотрение центров масс к решению геометрических задач, в результате были сформулированы теоремы Менелая и теоремы Чевы[2].
В случае систем материальных точек и тел в однородном гравитационном поле центр масс совпадает с центром тяжести, хотя в общем случае это разные понятия.
Центр масс в классической механике[править | править код]
Определение[править | править код]
Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом[3]:
где 


Для случая непрерывного распределения масс:
где 


Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.
Если система состоит не из материальных точек, а из протяжённых тел с массами 


Действительно, пусть даны несколько систем материальных точек с массами 


При переходе к протяженным телам с непрерывным распределением плотности в формулах будут интегралы вместо сумм, что даст тот же результат.
Иначе говоря, в случае протяжённых тел справедлива формула, по своей структуре совпадающая с той, что используется для материальных точек.
Примеры[править | править код]
- Центры масс плоских однородных фигур
- У отрезка — середина.
- У многоугольников :
- У параллелограмма — точка пересечения диагоналей.
- У треугольника — точка пересечения медиан (центроид).
- У правильного многоугольника — центр поворотной симметрии.
- У полукруга — точка, делящая перпендикулярный радиус в отношении
от центра круга.
Координаты центра масс однородной плоской фигуры можно вычислить по формулам (следствие из теорем Паппа — Гульдина):
и
, где
— объём тела, полученного вращением фигуры вокруг соответствующей оси,
— площадь фигуры.
- Центры масс периметров однородных фигур
- Центр масс сторон треугольника находится в центре вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Это означает то, что если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с центром вписанной окружности дополнительного треугольника или с центром Шпикера.
Использование[править | править код]
Понятие центра масс широко используется в физике, в частности, в механике.
Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.
Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.
Центр масс в релятивистской механике[править | править код]
В случае высоких скоростей (порядка скорости света) (например, в физике элементарных частиц) для описания динамики системы применяется аппарат СТО. В релятивистской механике (СТО) понятия центра масс и системы центра масс также являются важнейшими понятиями, однако, определение понятия меняется:
где 


Данное определение относится только к системам невзаимодействующих частиц. В случае взаимодействующих частиц в определении должны в явном виде учитываться импульс и энергия поля, создаваемого частицами[5].
Во избежание ошибок следует понимать, что в СТО центр масс характеризуется не распределением массы, а распределением энергии. В курсе теоретической физики Ландау и Лифшица предпочтение отдается термину «центр инерции». В западной литературе по элементарным частицам применяется термин «центр масс» (англ. center-of-mass): оба термина эквивалентны.
Скорость центра масс в релятивистской механике можно найти по формуле:
Смежные понятия[править | править код]
Центр масс vs. барицентр[править | править код]

Движение космических тел вокруг барицентра.
Термин «центр масс» синонимичен одному из значений понятия барицентр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр), однако последнее применяется преимущественно в задачах астрофизики и небесной механики. Под барицентром подразумевается общий для нескольких небесных тел центр масс, вокруг которого эти тела движутся. Примером может выступить совместное движение планеты и звезды (см. рис.) или компонент двойных звёзд. Центр масс (барицентр) в таком случае находится на отрезке длины 




Другое значение слова барицентр относится, скорее, к геометрии, нежели к физике; в этом значении выражение для координаты барицентра отличается от формулы для центра масс отсутствием плотности (как если бы всегда было 
Центр масс vs. центр тяжести[править | править код]
Центр тяжести (в данном случае = центр масс), демонстрация
Центр масс тела не следует путать с центром тяжести.
Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести (действующих на систему) равен нулю. Например, в системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибо вес P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.
В однородном гравитационном поле центр тяжести всегда совпадает с центром масс. В некосмических задачах гравитационное поле обычно может считаться постоянным в пределах объёма тела, поэтому на практике эти два центра почти совпадают.
По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (поскольку реального гравитационного поля нет, то и учёт его неоднородности не имеет смысла). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый.
См. также[править | править код]
- Классическая механика
- Теоретическая механика
- Теорема о движении центра масс системы
- Неваляшка
- Барицентр
- Центроид треугольника
Примечания[править | править код]
- ↑ Тарг С. М. Центр инерции (центр масс) // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 624—625. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- ↑ G. Ceva, De lineis rectis se invicem secantibus, statica constructio Milan, 1678
- ↑ Журавлёв, 2001, с. 66.
- ↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 2. Пространство. Время. Движение // Фейнмановские лекции по физике. — М.: Мир, 1965. — 164 с. — С. 68.
- ↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
Литература[править | править код]
- Бобылёв Д. К. Центр, в физике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Журавлёв В. Ф. Основы теоретической механики. 2-е изд. — М.: Физматлит, 2001. — 320 с. — ISBN 5-94052-041-3..
Тела, образующие
механическую систему, могут двигаться
в пространстве по различным направлениям.
Для суждения о перемещении механической
системы в целом вводится понятие центра
масс (ЦМ).
Центром
масс
называют точку, в которой как бы
сосредоточена вся масса системы.

Рис.
2.2
Рассмотрим
механическую систему материальных
точек, обладающих массами
![]() ,
,![]() ,
,
…![]() ,
,
положение которых характеризуется
радиус-векторами![]() ,
,![]() ,
,
…![]() (рис. 2.2).
(рис. 2.2).
Введем
понятие момента
массы,
равного произведению массы
![]() материальной точки на радиус-вектор
материальной точки на радиус-вектор![]() ,
,
определяющий ее положение, т.е.![]() .
.
Радиус-вектор
центра масс
находится из условия: момент центра
масс
![]() равен сумме моментов масс
равен сумме моментов масс![]() материальных точек, т.е.
материальных точек, т.е.
![]() ,
,
(2.9)
где
![]() и
и![]()
масса и радиус-вектор i-ой
материальной толчки, п
– число материальных точек в системе,
![]()
общая масса механической системы.
Отсюда, радиус-вектор центра масс
определяется выражением
 .
.
(2.10)
В
случае протяженных тел для нахождения
радиус-вектора центра масс поступают
следующим образом: мысленно тело
разбивают на элементарные участки
![]() ,
,
которые можно принять за материальные
точки. Тогда, согласно формуле (2.10),
радиус-вектор центра масс можно найти
как
 ,
,
(2.11)
где
интегрирование производится по всему
объему тела.
Для определения
положения центра масс достаточно
поочередно подвесить тело за две
различные точки на его поверхности и
провести через точки подвеса вертикали,
пересечение которых и даст положение
центра масс.
Скорость
центра масс.
Продифференцируем выражение (2.10) по
времени и получим
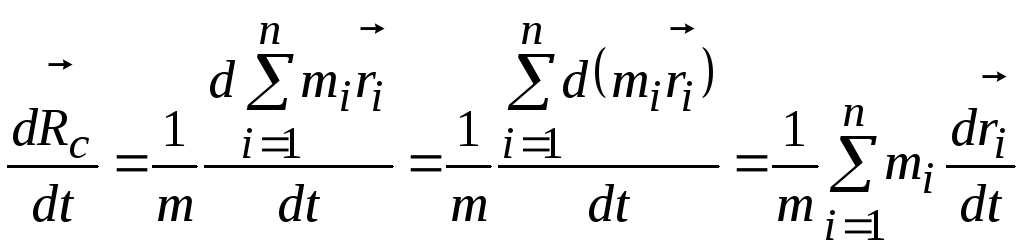
(учли,
что производная от суммы равна сумме
производных от каждого слагаемого, а
масса – величина постоянная и ее можно
вынести за знак производной).
Согласно
определению скорости можно записать,
что
![]()
скорость центра масс;
![]()
скорость отдельных материальных точек.
Тогда скорость центра масс
![]() .
.
(2.12)
Но
![]()
импульс механической системы, поэтому
![]() .
.
(2.13)
Таким
образом, импульс механической системы
описывается такой же формулой, как и
импульс материальной точки, но в данном
случае, скорость центра масс – это
скорость движения механической системы.
Ускорение
центра масс. Закон движения центра масс.
Продифференцируем
выражение (2.13) по времени и получим
![]() .
.
(2.14)
По
определению
![]()
ускорение центра масс системы. По второму
закону Ньютона для механической системы
![]() ,
,
где![]()
равнодействующая внешних сил, приложенных
к механической системе. Тогда
![]()
ускорение центра масс.
Таким образом,
центр масс механической системы движется
как материальная точка, в которой
сосредоточена масса всей системы, а
действующая сила равна геометрической
сумме всех внешних сил, приложенных к
системе.
Закон
движения центра масс.
![]() ,
,
(2.15)
где
![]()
равнодействующая всех внешних сил.
Если
механическая система замкнутая, то
![]() ,
,
тогда![]()
![]()
![]() ,
,
т.к. производная от постоянной величины
равна нулю.
Следовательно,
центр масс замкнутой механической
системы движется прямолинейно и
равномерно, в то время как отдельные
материальные точки системы могут
вращаться.
В силу того, что
скорость центра масс замкнутой системы
не меняется со временем, то, связав с
ним систему отсчета, получим некоторую
инерциальную систему отсчета. При
описании явлений в такой системе отсчета
исключаются усложнения, вносимые
движением системы.
Итак,
центр масс обладает следующими свойствами
свойствами:
1)
ускорение центра масс находится по
второму закону Ньютона;
2) центр
масс замкнутой системы движется
прямолинейно и равномерно (или неподвижен),
в то время как отдельные части системы
могут двигаться произвольно.
Соседние файлы в папке 432_lecfiz
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть система состоит из N материальных точек. Силы, действующие на i – ю точку, подразделяются на внутренние, действующие со стороны остальных точек системы, и внешние.
В соответствии с 3-м законом Ньютона сумма внутренних сил равна нулю:
Сумма всех сил, действующих на точки системы, равна сумме внешних сил, действующих на систему.
Если система не взаимодействует с внешними телами, то систему называют замкнутой или изолированной.
Центром масс (или центром инерции) системы материальных точек называют точку, положение которой определяется радиусом – вектором:
где mᵢ – масса материальной точки, rᵢ – радиус – вектор материальной точки, m – масса всей системы.
Центр масс системы совпадает с ее центром тяжести:
Центр тяжести – точка приложения равнодействующей для сил тяжести всех частей системы. Движение механической системы описывается движением ее центра масс:
Импульс центра масс системы равен сумме импульсов всех материальных точек системы.
Продифференцировав по времени верхнее уравнение (для Vc) получим уравнение движения центра масс:
Центр масс движется так, как двигалась бы воображаемая материальная точка с массой, равной массе системы, если к ней приложить результирующую внешнюю силу.
На нашем YouTube канале “Элементарная Физика”, в доступной и живой форме объясняются фундаментальные законы физики. Спасибо за внимание 🙂









