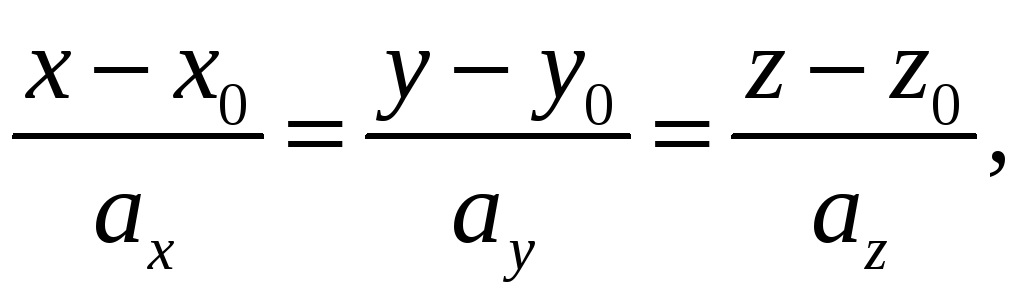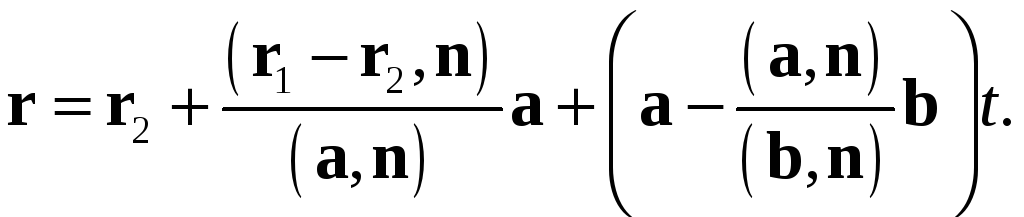1.5.
Лекция 5.
Прямая
в пространстве. Задачи о прямых
и
плоскостях
Уравнения
прямой, проходящей через данную точку
и параллельной данному вектору. Уравнение
прямой, проходящей через две заданные
точки. Расстояние от точки до прямой.
Расстояние между непараллельными
прямыми. Проекция точки на плоскость.
Проекция точки на прямую. Проекция
прямой на плоскость параллельно заданному
вектору. Общий перпендикуляр к двум
скрещивающимся прямым.
Уравнение
прямой, проходящей через данную точку
и
параллельной данному вектору
Существует,
причем единственная, прямая
,
содержащая заданную точку
и параллельная ненулевому вектору
.
Такой вектор называется направляющим
вектором прямой
.
Для произвольной точки
пространства имеем (рис. 10) логическую
цепочку
Уравнение
(5.1)
называется
векторным
уравнением прямой.
Вектор
называют вектором
сдвига
прямой.
Условие
параллельности векторов
и
можно записать в виде
,
или
.
(5.2)
Уравнение
(5.2) называется векторно-параметрическим
уравнением прямой.
Расписывая его в декартовой системе
координат, получим параметрические
уравнения прямой
(5.3)
Если
параметр
пробегает
,
точка с координатами
из (5.3) пробегает прямую.
Рис.
10. Уравнение прямой
Условие
(5.1) коллинеарности векторов в координатах
примет вид пропорции
(5.4)
где
.
Если
обращается в нуль одна из координат
направляющего вектора, например
,
то уравнения прямой принимают вид
Эта
прямая лежит в плоскости
.
Уравнение
прямой, проходящей через две заданные
точки
и
В
качестве направляющего вектора прямой
можно взять вектор
,
а в качестве данной точки прямой – точку
.
Тогда уравнение (5.1) примет вид
или
в координатах
Расстояние
от точки до прямой
Пусть
прямая
задана уравнением
,
а точка
– радиус-вектором
.
Расстояние от точки до прямой равно
можно найти, разделив площадь
параллелограмма, построенного на
векторах
и
,
на длину его основания (рис. 11).
Рис.
11. Расстояние от точки до прямой
В
результате получим формулу расстояния
от точки до прямой
(5.5)
Упражнение.
Записать расстояние от точки до прямой
в прямоугольных декартовых координатах.
Расстояние
между непараллельными прямыми
Рассмотрим
две непараллельные прямые
Существуют
параллельные плоскости
и
такие, что
.
В
качестве направляющих векторов обеих
плоскостей можно взять пару векторов
,
,
а в качестве начальных точек – точки с
радиус-векторами
и
,
соответственно, для плоскостей
,
.
Искомое расстояние между прямыми можно
найти, разделив объем параллелепипеда,
построенного на векторах
,
,
на площадь его основания (рис. 12). Получим
Рис.
12. Расстояние между непараллельными
прямыми
Из
приведенных рассуждений получаем также
Предложение.
Прямые
и
пересекаются тогда и только тогда, когда
Проекция
точки на плоскость
Найдем
радиус-вектор проекции точки
на плоскость
,
заданную уравнением
Прямая
проходит через
и перпендикулярна плоскости. Подставляя
значение для
из уравнения прямой в уравнение плоскости,
получим
.
Отсюда
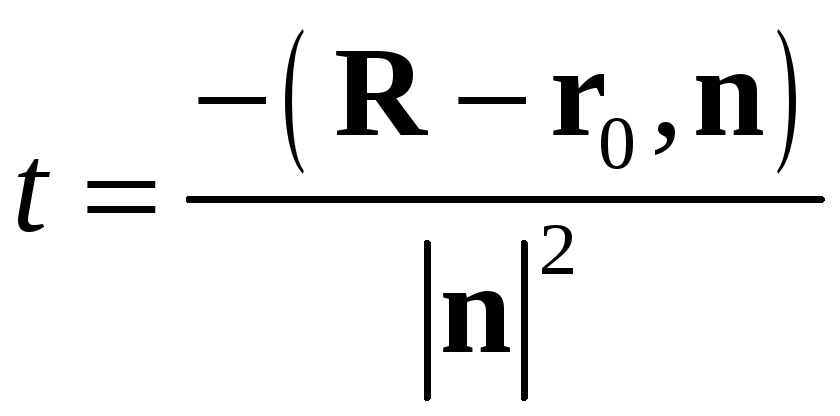
Подставив найденное значение
в уравнение прямой, получим радиус-вектор
искомой проекции
Проекция
точки на прямую
Пусть
прямая
задана уравнением
и дана точка
с радиус-вектором
.
Построим плоскость
,
перпендикулярную прямой
и проходящую через точку
.
В качестве нормального к плоскости
вектора можно взять вектор
,
а в качестве начальной точки плоскости
– точку
.
Тогда
есть уравнение искомой плоскости. Точка
пересечения этой плоскости с прямой
и есть проекция точки
на прямую
.
Найдем эту точку, решая относительно
и
систему уравнений
Подставляя
из первого уравнения во второе, получим
Отсюда
и

Подставляя
найденное значение
в первое уравнение системы, получим
радиус-вектор искомой точки
Проекция
прямой на плоскость параллельно заданному
вектору
Пусть
плоскость
задана уравнением
,
прямая
– уравнением
.
Требуется составить уравнение проекции
прямой
на плоскость
параллельно вектору
.
Будем считать, что векторы
не коллинеарны, ибо в противном случае
проекцией прямой на плоскость является
точка. Направляющий вектор
проекции можно искать в виде комбинации
,
перпендикулярной вектору
(рис. 13).
Рис.
13. Проекция прямой на плоскость
Так
как длина вектора с
нам безразлична, то мы можем положить
.
Из
условия
получим
и
Найдем
радиус-вектор точки пересечения плоскости
и прямой
.
Подставляя
значение
из уравнения прямой в уравнение плоскости,
получим
.
Отсюда
.
При этом значении
уравнение прямой даст искомый радиус-вектор
Имея
радиус-вектор
начальной точки проекции и ее направляющий
вектор
,
запишем, наконец, уравнение проекции
Другой
вариант решения этой задачи заключается
в построении проекции как пересечения
двух плоскостей: плоскости
и плоскости
,
порожденной векторами
и проходящей через точку пересечения
прямой
с плоскостью
.
Общий
перпендикуляр к двум скрещивающимся
прямым
Пусть
прямые
и
не
параллельны, т.е..
Вектор
перпендикулярен обеим прямым. Поэтому
плоскость
(5.6)
проходит
через первую прямую и общий перпендикуляр,
а плоскость
(5.7)
– через
вторую прямую и общий перпендикуляр к
обеим прямым. Следовательно, общий
перпендикуляр можно задать системой
уравнений (5.6) и (5.7) как пересечение
плоскостей. Чтобы найти его начальную
точку, можно решить совместно уравнение
первой прямой и уравнение плоскости
(5.7). Направляющим вектором является
вектор
.
Рассмотрим
другой способ решения этой задачи. На
первой прямой возьмем произвольную
точку
с радиус-вектором
,
а на второй – точку
с радиус-вектором
.
Подберем значения параметров
так, чтобы вектор
был
перпендикулярен обоим векторам
и
.
Для этого мы должны решить относительно
систему
Преобразуем
ее
к
виду
Главный
определитель этой системы
отличен
от нуля. По правилу Крамера эта система
имеет единственное решение
Тем
самым определятся точки
и
.
Осталось записать уравнение прямой
через эти точки.
Изложенный
метод годится для построения общего
перпендикуляра к двум скрещивающимся
прямым в пространстве размерности и
выше трех.
Упражнения
5.1.
Точка
определяется радиус-вектором
.
Составить уравнение прямой, проходящей
через точку
перпендикулярно плоскости
.
5.2.
Точка
определяется радиус-вектором
.
Составить уравнение плоскости, проходящей
через точку
перпендикулярно прямой
.
5.3.
Составить векторное уравнение плоскости,
проходящей через прямую
и
точку
,
не лежащую на этой прямой.
5.4.
Даны точка
и плоскость
.
Найти радиус-вектор точки
,
симметричной с
относительно плоскости.
5.5.
Даны точка
и прямая
.
Найти радиус-вектор точки
,
симметричной с
относительно прямой.
5.6.
Составить уравнение прямой, пересекающей
прямую
под прямым углом и проходящей через
точку
,
не лежащую на данной прямой (перпендикуляра,
опущенного из точки
на прямую
.
5.7.
Составить уравнение прямой, пересекающей
две скрещивающиеся прямые
и
и проходящей через точку
,
не лежащую ни на одной из этих прямых.
5.8.
Найти расстояние между двумя параллельными
плоскостями
и
.
5.9.
Составить уравнение прямой, которая
параллельна прямой
и пересекает прямые
,
.
Вопросы
для самопроверки
1.
Дайте геометрическую иллюстрацию
векторно-параметрическому уравнению
прямой.
2.
Как перейти от векторно-параметрического
уравнения прямой к каноническим и
параметрическим уравнениям?
3.
Как найти направляющий вектор прямой,
проходящей через две заданные точки?
4.
Как найти направляющий вектор прямой,
являющийся пересечением двух плоскостей?
33
Соседние файлы в папке Analiticheskaya_geom
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое радиус-вектор
Радиус-вектор – это вектор, начало которого совпадает с точкой (0 ; 0) — началом координат.
Почему радиус-вектор так называют
Если начертить окружность с центром в точке (0 ; 0), этот вектор станет её радиусом.
Любой вектор можно превратить в радиус-вектор. Для этого сдвигаем его так, чтобы начало этого вектора совместить с точкой (0 ; 0).
При этом, помним: перемещать вектор можно, а поворачивать его нельзя!
Чем радиус-вектор удобен для использования
Чтобы найти координаты вектора, нужно найти разности соответственных координат точек, расположенных в конце и начале вектора.
Для радиус-вектора вычислять координаты не нужно. Можно воспользоваться правилом:
Координаты радиус-вектора — это координаты его конечной точки.
Сравните координаты конечной точки и координаты вектора на рисунке 2.
Как найти радиус вектора
Получите бесплатный курс по основам математики. Эти знания необходимы для решения задач по физике.
Векторная алгебра с нуля!
Получите бесплатный курс по Векторной алгебре. Он необходим для решения задач по физике.
Книги по изучению физики и для подготовки к ЕГЭ
Радиус-вектор
Радиус-вектор точки – это вектор, начало которого совпадает с началом системы координат, а конец – с данной точкой.
Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат (рис. 17).
Введение понятия радиус-вектора оказалось чрезвычайно плодотворным при изучении различных физических явлений. В частности, это понятие широко используется в механике.
Как известно, положение точки можно задать с помощью ее координат. Так, если известны координаты x1 и y1 точки В или координаты x2 и y2 точки С, то мы легко находим положения этих точек на плоскости. Этот способ определения положения точки с помощью ее координат называется координатным способом.
Но можно определить положение точки и по-другому, а именно с помощью радиус-вектора. Если известен радиус-вектор данной точки, то и ее положение оказывается известным, поскольку точка конца радиус-вектора совпадает с данной точкой. Так, положение точки В – это конец ее радиус-вектора r1, а положение точки С – это конец ее радиус-вектора r2. Этот способ определения положения точки с помощью ее радиус-вектора называется векторным способом.
Эти способы эквивалентны друг другу. Покажем это. Найдем проекции радиус-вектора r1 точки В на координатные оси. Напомню, чтобы найти проекцию вектора на ось нужно из координаты конца вектора вычесть координату его начала. Тогда
Аналогично для проекций радиус-вектора r2 точки С:
r2y = y2 − 0 = y2. Таким образом, проекции радиус-векторов точек являются координатами этих точек (рис. 18).
На практике применяются как координатный, так и векторный способы. Более того, при решении многих задач их применяют совместно, что является мощным методом решения, поскольку он позволяет использовать единый подход для решения совершенно разных задач.
Книги по изучению физики и для подготовки к ЕГЭ
Эти книги должен иметь каждый старшеклассник, абитуриент и студент!
Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).
© Коллекция подготовительных материалов для успешной сдачи ЕГЭ по физике от Н. Чернова 2012 – 2015 | Контакты: , +79212839427, (81554) 65780
Физика
А Вы уже инвестируете?
Слышали про акцию в подарок?
Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб
План урока:
Механическое движение. Система отсчёта. Закон относительности движения
Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.
То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).
Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.
Рисунок 1 – Иллюстрация к примеру
Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.
Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.
Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)
Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.
Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.
Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.
Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.
Уравнения движения. Радиус-вектор. Проекция вектора
Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?
Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:
Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.
Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.
В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).
Еще один способ описания движения – векторный.
*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»
Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).
Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r1 и r2* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)
Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:
r = r(t)
Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.
Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.
*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.
Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).
Рисунок 4 – Построение проекции вектора на ось
Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, – это и есть искомая проекция.
Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.
Напоминания из геометрии:
два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;
проекции равных векторов равны.
Рассмотрим пример (см. рисунок 5)
Рисунок 5 – Задача на нахождение проекции векторов
Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.
Итак, вектор а: его начала соответствует координате хн=1, а конец хк = 4. Значит ax = хк – хн = 4-1 = 3. Вектор b: его начало лежит в точке хн=2, а конец хк =0. Значит bx = хк – хн = 0-2 = -2.
В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.
Иногда еще нужно находить составляющие компоненты вектора ах и ау. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).
Сумма векторов ах и ау равна а. Модули векторов ах и ау численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.
Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:
Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины ах и ау совпадали бы с координатами тела по осям ОХ и ОY.
Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.
Рисунок 6 – Нахождение компонент вектора а
Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.
Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве
В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.
Точки, в которые попал перпендикуляры к осям – rx, ry, rz – это и есть координаты x, y, z тела в текущий момент времени.
Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.
Рисунок 8 – Построение проекций радиус-вектора
Траектория. Путь. Перемещение
Траектория – это линия, вдоль которой движется тело.
Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.
Путь (S), пройденный телом, равен длине траектории.
Перемещение (r)* – это вектор, проведенный из начала пути в конец.
В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.
Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении
*Иногда перемещение так же, как и путь, называют буквой S – (на письме с вектором над ней, при печати – жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.
Равномерное прямолинейное движение: скорость и уравнение движения
Путь и перемещение при равномерном прямолинейном движении
Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.
Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:
- равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.
Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.
Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r0, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.
Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении
Тогда скорость движения (v) будет вычисляться по формуле:
Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.
Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r1 – r0. Тогда выражение для скорости можно переписать в виде:
Из этого выражения следует:
Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:
Данное уравнение является уравнением движения при прямолинейном равномерном движении.
*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t1, где t – конечный момент времени, t1 – начальный. Если же начальный момент времени совпадает с началом отсчета t1 = 0, то △t = t – 0 = t.
Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.
Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.
В этих выражениях r0x, r0y, r0z и vx, vy, vz – это компоненты изначальных векторов r0 и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:
Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.
В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х0) и конечной (х1) точки на ось ОХ.
Рисунок 9 – Перемещение тела в координатном представлении
Уравнение координаты (х) движения будет выглядеть:
А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:
Если точка начала двигаться из начала отсчета S0 = 0, можно переписать эту формулу в виде:
Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:
Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x0 = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.
Итак, для начала приведем все единицы измерения к СИ:
Теперь можно записывать уравнение для координаты х:
Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:
x(2) = 0,03 + 5*2 = 10, 03.
А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:
S = x(2) – x0 = 10, 03 – 0,03 = 10 м.
А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?
Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:
[spoiler title=”источники:”]
http://cours.su/Vektory/radius_vektor.html
http://100urokov.ru/predmety/kinematika-tverdogo-tela-chast-1
[/spoiler]
Пусть проекции точки М на координатные оси будут М(х;у;z). Вектор 

Выражение координат вектора через координаты начала и конца.
Пусть известны координаты начала и конца вектора А( 


Для нахождения координат вектора необходимо: из координат конца вектора вычесть координаты его начала.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10618 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Описание файла
PDF-файл из архива “Семинар — Решения некоторых задач к экзамену по аналитической геометрии”, который расположен в категории “лекции и семинары”. Всё это находится в предмете “аналитическая геометрия и линейная алгебра” из первого семестра, которые можно найти в файловом архиве МГУ им. Ломоносова. Не смотря на прямую связь этого архива с МГУ им. Ломоносова, его также можно найти и в других разделах. .
Просмотр PDF-файла онлайн
Текст 3 страницы из PDF
Будем искать уравнение ортогональной проекции вследующем виде:r = r1 + bt.Найдём сначала радиус–вектор r1 , как точку пересечения прямой иплоскости:(r1 , n) = D, r1 = r0 + t0 a,213. Прямые и плоскости····Рис. 14. К задаче 21.r1 = r0 +D − (r0 , n)a при (a, n) 6= 0.(a, n)Найдём теперь направляющий вектор b как ортогональную проекциюна плоскость вектора a :(a, n) = λ(n, n),(a, n)n.b=a−(n, n)a = b + λn,Итак,D − (r0 , n)(a, n)r = r0 +a+ a−n t.(a, n)(n, n)З а д а ч а 22. Прямая задана как пересечение двух плоскостей(r, n1 ) = D1 и (r, n2 ) = D2 . Запишите векторное параметрическое уравнение этой прямой, т.е.
уравнение вида r = r0 + ta.Р е ш е н и е . Направляющий вектор искомой прямой равен a == [n1 , n2 ]. Будем искать радиус–вектор r0 как пересечение трёх плоскостей:(r0 , n1 ) = D1 , (r0 , n2 ) = D2 , (r0 , a) = 0.Решение этой системы уравнений имеет следующий вид:r0 =D1 [n2 , a] + D2 [a, n1 ]|[n1 , n2 ]|2.З а д а ч а 23. Найдите радиус-вектор точки пересечения прямой[r, a] = b с плоскостью (r, n) = D.Р е ш е н и е . Перепишем уравнение прямой в следующем виде:r = r0 + at,r0 =[a, n].(a, a)22Семинар 1. Решение задач к экзамену по курсу «Аналитическая Геометрия»Поскольку прямая и плоскость пересекаются, то (a, n) 6= 0. Поэтомупосле подстановки векторного параметрического уравнения прямой вуравнение плоскости получим, чтоt0 =D − (r0 , n).(a, n)Итак,r = r0 +D − (r0 , n)a.(a, n)З а д а ч а 24.
Найдите проекцию точки M0 (r0 ) на плоскость (r, n) == D параллельно прямой r = r1 + ta при условии (a, n) 6= 0.Р е ш е н и е . Заметим, что просто нужно найти радиус–вектор r2точки пересечения прямой r = r0 + at и плоскости (r, n) = D. В результате получим (смотри задачу 23)r2 = r0 +D − (r0 , n)a.(a, n)З а д а ч а 25. Найдите проекцию точки M0 (r0 ) на прямую r = r1 ++ ta параллельно плоскости (r, n) = D при условии (a, n) 6= 0.Р е ш е н и е .
Нужно найти радиус–вектор r2 точки пересеченияплоскости (r − r0 , n) и прямой r = r1 + ta. Действительно, имеемr2 = r1 +(r1 − r0 , n)a.(a, n)З а д а ч а 26. Найдите ортогональную проекцию точки M0 (r0 ) напрямую [r, a] = b.Р е ш е н и е . Пусть M2 (r2 ) — это искомая точка ортогональной проекции точки M0 (r0 ) на прямую. Тогда выполнено следующее условие:−−−−→ M0 M2 , a = 0 ⇔ (r2 − r0 , a) = 0.Поскольку r2 = r1 + at0 при некотором t0 , то имеемt0 =(r0 − r1 , a),(a, a)r2 = r1 +(r0 − r1 , a)a.(a, a)З а д а ч а 27.
Найдите ортогональную проекцию точки M0 (r0 ) наплоскость r = r0 + ua + vb.Р е ш е н и е . Нужно найти точку M2 (r2 ) пересечения прямой r == r0 + t[a, b] и плоскости (r − r1 , [a, b]) = 0. Итак,r2 = r0 +(r1 − r0 , [a, b])|[a, b]|2[a, b].З а д а ч а 28. Найдите расстояние между двумя параллельнымиплоскостями r = r1 + ua + vb и r = r2 + ua + vb.3. Прямые и плоскости23Р е ш е н и е . Общая формула для вычисления расстояния от точкиM1 (r1 ) до плоскости (r, n) = D имеет следующий вид:d=|(r1 , n) − D|.|n|Исходя из этой формулы получаемd=|(r1 − r2 , [a, b])|.|[a, b]|З а д а ч а 29.
Найдите расстояние между двумя параллельнымиплоскостями (r, n) = D1 и (r, n) = D2 .Р е ш е н и е . В соответствии с предыдущей задачей имеемd=|D − D1 ||(r2 , n) − D1 |= 2.|n||n|З а д а ч а 30. Найдите расстояние от точки M0 (r0 ) до прямой[r, a] = b.Р е ш е н и е . Запишем уравнение прямой [r, a] = b в векторнойпараметрической формеr = r1 + at,r1 =[a, b].(a, a)Пусть M2 (r2 ) — это ортогональная проекция точки M0 (r0 ) на прямую.Тогда в силу задачи 26 имеемr2 = r1 +(r0 − r1 , a)(r , a)a = r1 + 0a.(a, a)(a, a)Таким образом, имеем [a, b] + (r0 , a)a− r0 .d = |r2 − r0 | = (a, a)З а д а ч а 31.
Составьте уравнение плоскости, содержащей параллельные прямые r = r1 + ta и r = r2 + ta.Р е ш е н и е . Очевидно, уравнение следующее:(r − r1 , [r2 − r1 , a]) = 0.З а д а ч а 32. Найдите расстояние между параллельными прямымиr = r1 + ta и r = r2 + ta.Р е ш е н и е . С одной стороны, площадь треугольника △A1 A2 A3равнаSA1 A2 A3 = |[r1 − r2 , a]| .С другой стороны, равнаSA1 A2 A3 = h|a|,24Семинар 1.
Решение задач к экзамену по курсу «Аналитическая Геометрия»··h··Рис. 15. К задаче 32.где h — это искомое расстояние. Итак, имеемh=|[r1 − r2 , a]|.|a|З а д а ч а 33. Найдите расстояние между параллельными прямыми[r, a] = b1 и [r, a] = b2 .Р е ш е н и е . Запишем уравнения этих прямых в векторной параметрической форме:r = r1 + at,r1 =[a, b1 ],(a, a)r = r2 + at,r1 =[a, b2 ].(a, a)Тогда в соответствии с задачей 32 получимh=|[r1 − r2 , a]||b1 − b2 |=.|a||a|З а д а ч а 34. Составьте уравнение плоскости, проходящей черезлинию пересечения плоскостей (r, n1 ) = D1 и (r, n2 ) = D2 перпендикулярно плоскости (r, n3 ) = D3 .Р е ш е н и е . По условию задачи векторы [n1 , n2 ] и n3 параллельныплоскости. Предположим, что [n3 , [n1 , n2 ]] 6= ϑ.
Тогда уравнение искомой плоскости имеет следующий вид:(r − r0 , n) = 0,n = [n3 , [n1 , n2 ]].Осталось найти радиус–вектор r0 какой–нибудь точки M0 , лежащейна плоскости. Будем искать эту точку как точку пересечения трёхплоскостей:(r0 , n1 ) = D1 ,(r0 , n2 ) = D2 ,(r0 , [n1 , n2 ]) = 03. Прямые и плоскости25Таким образом, имеемr0 =D1 [n2 [n1 , n2 ]] + D2 [[n1 , n2 ], n1 ]|[n1 , n2 ]|2З а д а ч а 35. Составьте уравнение плоскости, проходящей черезточку M0 (r0 ) и прямую [r, a] = b.Р е ш е н и е .
Запишем уравнение прямой в векторной параметрической форме:[a, b]r = r1 + at, r1 =.(a, a)Тогда уравнение плоскости имеет следующий вид:(r − r0 , [r1 − r0 , a]) = 0.З а д а ч а 36. Найдите расстояние между скрещивающимися прямыми [r, a1 ] = b1 и [r, a2 ] = b2 .Р е ш е н и е . Запишем уравнения прямых в векторной параметрической форме[a1 , b1 ]r = r 1 + a 1 t, r 1 =;(a1 , a1 )[a2 , b2 ].r = r 2 + a 2 t, r 2 =(a2 , a2 )Тогда искомое расстояние равноh=|(r1 − r2 , [a1 , a2 ])|.|[a1 , a2 ]|Справедливы следующие равенства:1([a1 , b1 ], [a1 , a2 ]) = (b1 , a2 ),(a1 , a1 )(r2 , [a1 , a2 ]) = −(a1 , b2 ).(r1 , [a1 , a2 ]) =Тогда приходим к следующей формуле:h=|(b1 , a2 ) + (a1 , b2 )|.|[a1 , a2 ]|.
Даны прямая $%r=r_0+at$% и плоскость $%(r,n)=D$%, не параллельные между собой. Точка $%M$% лежит на прямой и удалена от плоскости на расстояние $%p$%. Найти радиус-вектор точки $%M$%.
задан 25 Окт ’14 18:47
Uchenitsa
1.3k ● 18 ● 80
97% принятых
Если не составлять каких-то специальных формул векторной алгебры, то решить можно так. Берём известную формулу для расстояния от точки до плоскости, заданной уравнением. Если не путаю, она имеет вид $%frac<|Ax+bY+Cz-D|><sqrt>$%. Вместо координат подставляем выраженные через $%t$% координаты точки прямой из параметрического уравнения. Приравниваем расстояние к числу $%p$% и находим два значения $%t$%. Потом его подставляем в уравнение прямой и получаем радиус-вектор.
@falcao, спасибо за решение! Я решила с помощью векторов, не раскладывая на координаты, но Ваш метод мне помог
| Поделитесь ссылкой пожалуйста: |
Как найти радиус вектор точки
Радиус-вектор в декартовых координатах
Радиус-вектор точки — это называется вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.
Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат (рис. 17).
Введение понятия радиус-вектора оказалось чрезвычайно плодотворным при изучении различных физических явлений. В частности, это понятие широко используется в механике.
Как известно, положение точки можно задать с помощью ее координат. Так, если известны координаты x1 и y1 точки В или координаты x2 и y2 точки С, то мы легко находим положения этих точек на плоскости. Этот способ определения положения точки с помощью ее координат называется координатным способом.
Модуль радиус-вектора
— по теореме Пифагора.
Механическое движение. Система отсчета. Материальная точка.
Механическое движение – это процесс изменения положения данного тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным.
Тело, условно принятое за неподвижное – тело отсчета.
Тело отсчета – это тело, относительно которого опре-деляется положение другого тела.
Обычно в качестве тела отсчета выбирается земля, но может быть и движущийся относительно земли предмет: автомобиль, лодка, самолет и т.д.
Система отсчета – это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения.
Простейшей системой координат является прямоугольная декартова система (рис. 2). Система координат нужна для определения положения тела относительно тела отсчета. Выбор системы отсчета зависит от условий дан-ной задачи.
Движение реальных тел, как правило, сложное. Для упрощения рас-смотрения движений пользуются моделями. Одними из первых моделей реальных тел являются абсолютное твердое тело и материальная точка.
Материальной точкой называется тело, размерами и формой которого можно пренебречь в данной задаче. Данное понятие является математической абстракцией. Одно и то же тело в одних задачах можно рассматривать как материальную точку, а в других задачах – нельзя. Например, радиус Земли RЗемли равен 6400 км, расстояние между Солнцем и Землей L равно 150 000 000 км (L >> RЗемли). Рассматривая движение Земли относительно Солнца, радиусом Земли можно пре-небречь и считать, что Земля – материальная точка. Однако если нужно выяснить причины смены времен года, то Землю уже нельзя считать матери-альной точкой, а надо учитывать ее размеры, вращение вокруг оси и т.д. Мы будем изучать механическое движение материальной точки для того, чтобы потом определить движение реального тела.
Радиус-вектор. Проекции радиус-вектора. Модуль радиус-вектора.
Ра?диус-ве?ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат.
Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.
Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.
Радиус-вектор в декартовых координатах
Радиус-вектор точки — это называется вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.
Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат (рис. 17).
Введение понятия радиус-вектора оказалось чрезвычайно плодотворным при изучении различных физических явлений. В частности, это понятие широко используется в механике.
Как известно, положение точки можно задать с помощью ее координат. Так, если известны координаты x1 и y1 точки В или координаты x2 и y2 точки С, то мы легко находим положения этих точек на плоскости. Этот способ определения положения точки с помощью ее координат называется координатным способом.
— по теореме Пифагора.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10572 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Физика и техника.
Физика тесно связана и с техникой, причем эта связь имеет двусторонний характер.
Физика выросла из потребностей техники. Так, развитие механики у древних греков было вызвано запросами строительной и военной техники того времени.
Развитие техники, в свою очередь, определяет направление физических исследований. Например, в свое время задача создания наиболее экономичных тепловых двигателей вызвала бурное развитие термодинамики. А началось все с того, что Джеймс Уатт заметил, что крышка кипящего чайника немного приподнимается под действием пара.
С другой стороны, от развития физики зависит технический уровень производства.
Физика лежит в основе создания новых отраслей техники (электронная техника, ядерная техника и др.).
Бурный темп развития физики, растущие связи ее с техникой указывают на значительную роль курса физики во втузе.
Физика является фундаментальной основой для теоретической подготовки инженера, без которой его успешная практическая деятельность невозможна.
Развитие механики как науки начинается с III в. до н. э., когда древнегреческий ученый Архимед (287—212 до н. э.) сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564—1642) и окончательно сформулированы английским ученым И. Ньютоном (1643—1727).
Механическим движением называется изменение положения тела относительно других тел с течением времени.
Материальной точкой называется тело, размерами и формой которого в данных условиях можно пренебречь.
Положение материальной точки указывается при помощи радиус-вектора 

где 

Модуль радиус-вектора вычисляется по формуле:
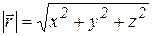
Единичным вектором 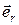


Если положение точки в пространстве изменяется, то радиус-вектор зависит от времени:
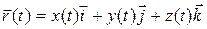
Это векторная форма кинематического закона движения точки.
Конец радиус-вектора при движении точки описывает в пространстве кривую, называемую траекторией движения точки. Зависимость (1.4) эквивалентна системе уравнений:
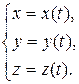
Зависимость вида (1.5) называется координатной формой кинематического закона движения точки.
Расстояние между двумя положениями 1 и 2 материальной точки в пространстве определяется по формуле:

где 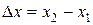
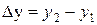
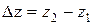

Действительно, из рисунка 1.1 видно, что вектор 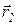
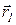
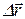
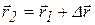
С другой стороны вектор перемещения может быть представлен через разности координат:
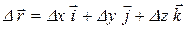
Поэтому модуль вектора перемещения из точки 1 в точку 2 определяется по формуле (1.6).
Изменение положения материальной точки с течением времени характеризуется вектором мгновенной скорости, который определяется как производная от радиус-вектора материальной точки по времени[1]:
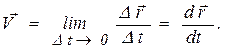
Вектор мгновенной скорости точки направлен по касательной к траектории в сторону движения точки. Его можно представить в виде:

где проекции 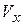



С другой стороны, радиус-вектор материальной точки можно представить в виде:

где 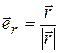
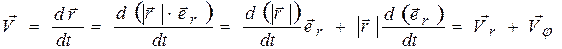
Первая составляющая: 

Вторая составляющая: 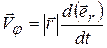

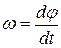


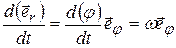
В целях наглядности, рассмотренные кинематические характеристики 
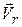
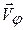
Модуль вектора мгновенной скорости определяется следующим образом:
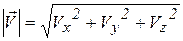
Направление вектора мгновенной скорости определяется при помощи направляющих косинусов:

Средняя скорость 


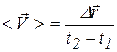
где 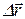
Из предыдущей формулы следует, что перемещение можно выразить через среднюю скорость перемещения:
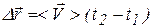
Путь определяют как длину дуги между точками 1 и 2. При смещении материальной точки вдоль траектории на бесконечно малую величину, ее путь можно записать следующим образом:

Проинтегрировав полученное выражение по времени от 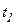
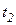

где 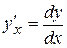
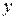
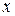


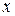
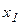
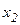

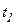
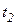
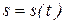
Изменение вектора скорости с течением времени характеризуется вектором мгновенногоускорения, который определяется как производная от вектора скорости по времени:

Вектор ускорения материальной точки можно представить в виде:
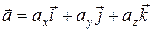
где 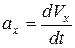
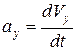
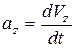
Модуль вектора ускорения вычисляется следующим образом:
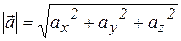
Направляющие косинусы вектора ускорения равны
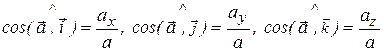
Ускорение характеризует изменение величины и направления скорости в целом. Оно может быть представлено в виде векторной (геометрической) суммы тангенциального и нормального ускорений:

Модуль ускорения выражается через модули тангенциального и нормального ускорений при помощи теоремы Пифагора:

Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9465 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.
Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .
Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .
По условию известно, что A B → = ( 2 , 0 , — 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Ра́диус-ве́ктор (обозначается буквой 


Радиус-вектор в геометрии[править | править код]
Для произвольной точки в пространстве радиус-вектор — это вектор, идущий из начала координат в эту точку.
Длина, или модуль радиус-вектора — расстояние, на котором точка находится от начала координат, стрелка вектора — указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.
Запись в различных системах координат[править | править код]
Двумерное пространство[править | править код]
Трёхмерное пространство[править | править код]
n-мерное пространство[править | править код]
- Декартовы координаты:
Радиус-вектор в кинематике[править | править код]
В кинематике изменение радиус-вектора со временем, то есть функция 
-
,
где точка сверху обозначает дифференцирование по времени, а две точки — двукратное дифференцирование.
В таком виде запись применима к системе координат любого типа. Но переход к трём координатам декартовой, цилиндрической и сферической систем осуществляется по-разному. Например, если для декартовых координат