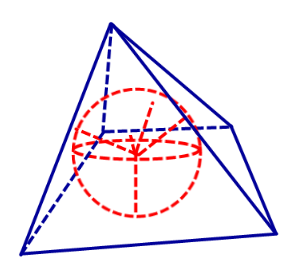
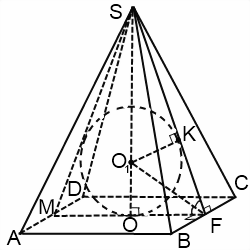
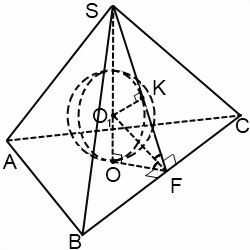
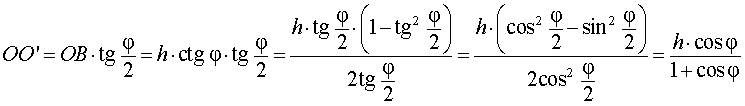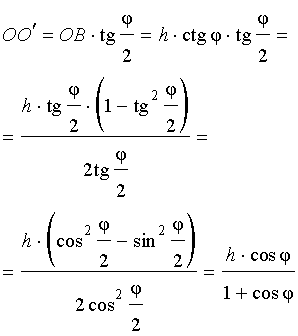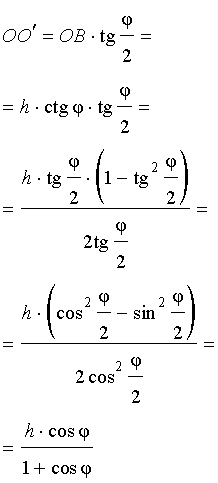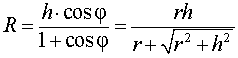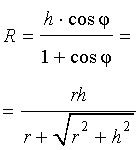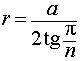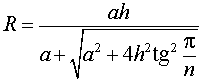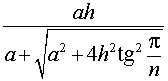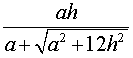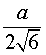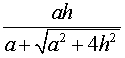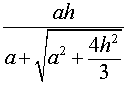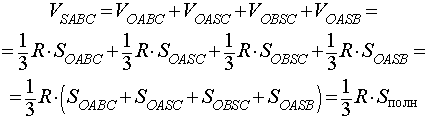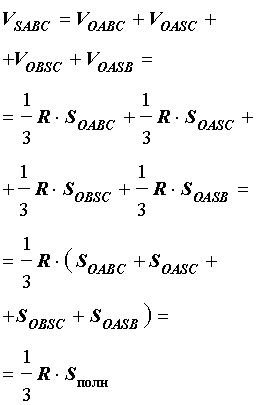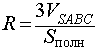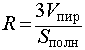В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.
-
Формулы расчета радиуса шара (сферы)
- Правильная треугольная пирамида
- Правильная четырехугольная пирамида
-
Правильная шестиугольная пирамида
Формулы расчета радиуса шара (сферы)
Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.
Правильная треугольная пирамида
На рисунке:
- a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;
- DE – высота пирамиды (h).
Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:
Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:
Правильная четырехугольная пирамида
На рисунке:
- a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
- EF – высота пирамиды (h).
Радиус (r) вписанного шара/сферы рассчитывается так:
Правильная шестиугольная пирамида
На рисунке:
- a – ребро основания пирамиды, т.е. AB, BC, CD, DE, EF, AF;
- GL – высота пирамиды (h).
Радиус (r) вписанного шара/сферы вычисляется по формуле:
Все формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
a , b , c – стороны треугольника
p – полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Радиус вписанной окружности в равносторонний треугольник
a – сторона треугольника
r – радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a – равные стороны равнобедренного треугольника
b – сторона ( основание)
α – угол при основании
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a – равные стороны равнобедренного треугольника
b – сторона ( основание)
h – высота
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Нахождение радиуса шара (сферы), вписанного в правильную пирамиду
В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.
Формулы расчета радиуса шара (сферы)
Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.
Правильная треугольная пирамида
-
a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;
Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:
Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:
Правильная четырехугольная пирамида
- a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
- EF – высота пирамиды (h).
Радиус (r) вписанного шара/сферы рассчитывается так:
Правильная шестиугольная пирамида
- a – ребро основания пирамиды, т.е. AB, BC, CD, DE, EF, AF;
- GL – высота пирамиды (h).
Радиус (r) вписанного шара/сферы вычисляется по формуле:
Сфера, вписанная в пирамиду
Биссекторная плоскость. Основное свойство биссекторной плоскости
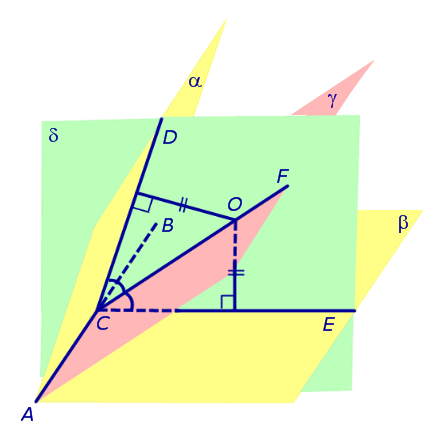
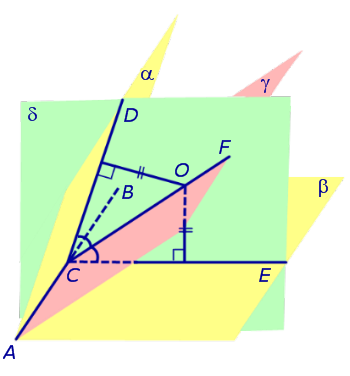
Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).
Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.
Доказательство. Рассмотрим произвольную точку O, расположенную внутри двугранного угла, и проведем через эту точку плоскость δ , перпендикулярную к ребру AB двугранного угла (рис. 2).
Плоскость δ пересекает ребро AB двугранного угла в точке C, а грани двугранного угла α и β по лучам CD и CE соответственно. Угол DCE является линейным углом двугранного угла. Биссекторная плоскость γ пересекает плоскость δ по биссектрисе CF линейного угла DCE .
Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.
Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).
Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы
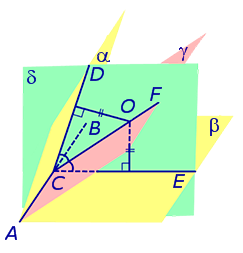
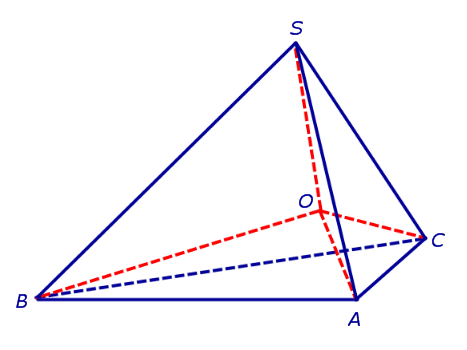
Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).
Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.
Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.
Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.
Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.
Рассмотрим несколько типов пирамид, в которые можно вписать сферу.
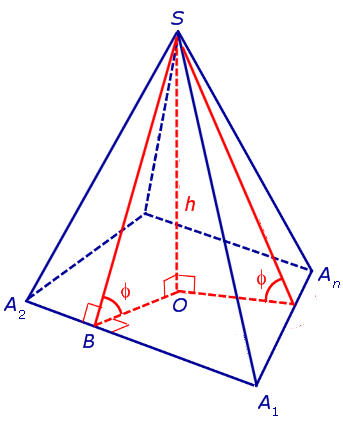
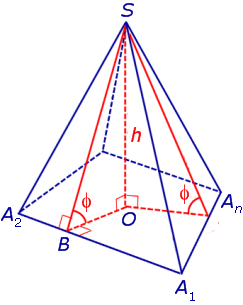
Утверждение 2. Если у пирамиды SA1A2 . An основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A1A2 . An , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.
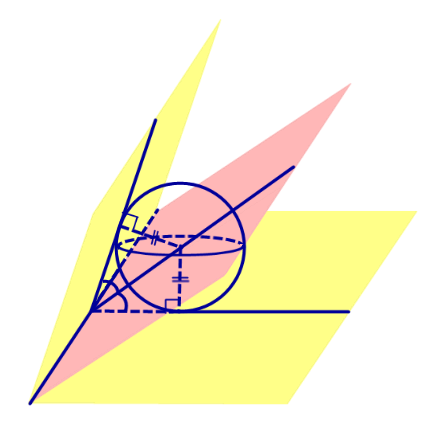
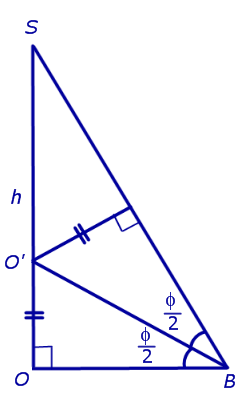
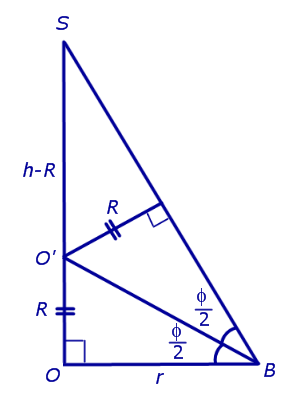
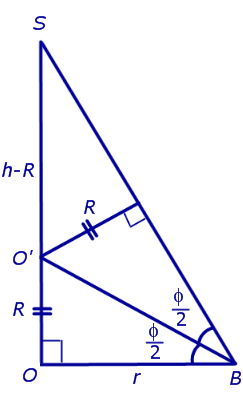
Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA1A2 и проведем в ней высоту SB (рис. 5).
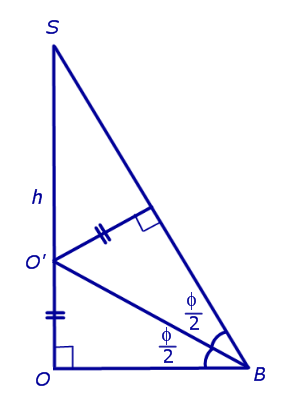
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A1A2 . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA1A2 и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).
Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле
Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле
Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.
Доказательство утверждения 2 завершено.
Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо
Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле
 |
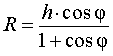(1) |
Радиус сферы, вписанной в правильную n – угольную пирамиду
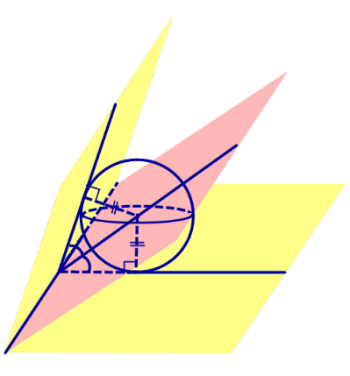
Решение. Рассмотрим правильную n – угольную пирамиду SA1A2 . An и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).
Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем
 |
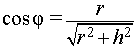(2) |
В силу следствия 2 из формул (1) и (2) получаем
из формулы (3) получаем соотношение
Ответ. 
Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен
Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен
Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен
Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен
Сфера, вписанная в треугольную пирамиду.
Формула для радиуса вписанной сферы
Утверждение 3. В любую треугольную пирамиду можно вписать сферу.
Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.
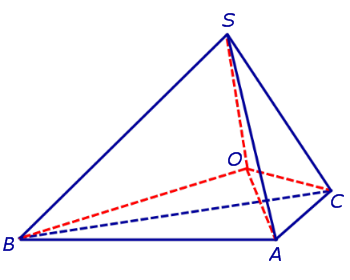
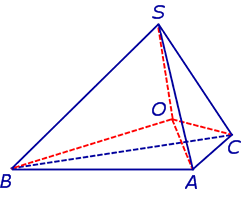
Действительно, пусть SABC – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром AC и биссекторная плоскость внутреннего двугранного угла с ребром AB пересекаются по некоторой прямой, проходящей через вершину A. Биссекторная плоскость внутреннего двугранного угла в ребром BC пересекает эту прямую в единственной точке O , которая и является центром вписанной сферы (рис. 8).
Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами
а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами
то справедливы следующие равенства:
где символом Sполн обозначена площадь полной поверхности пирамиды SABC.
Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы
где символами Vпир и Sполн обозначены объем и площадь полной поверхности пирамиды соответственно.
[spoiler title=”источники:”]
http://www.resolventa.ru/spr/stereometry/sphere_piramide.htm
[/spoiler]
Перед тем, как смело броситься на амбразуру решения задачи по нахождению радиуса сферы, нужно узнать, что вообще такое сфера и шар. Стереометрия говорит нам, что сфера – это поверхность, состоящая из массы точек пространства, которые находятся на одном расстоянии от центра. Эта точка – центр сферы, а радиус сферы (R) – это расстояние, на которое каждая точка удалена от центра сферы. Шар – это тело, которое ограничено поверхностью сферы.
Безусловно, способ определения того самого радиуса сферы будет зависеть от данных, которые у нас есть.
Способ 1. Определение радиуса сферы при помощи площади ее поверхности
Допустим, нам дана сфера вместе с площадью её поверхности. В таком случае мы будем использовать формулу площади её поверхности для того, чтобы вычислить радиус.
где S – это площадь поверхности сферы, число Пи = 3,14.
Способ 2. Определение радиуса сферы при помощи объема шара
Если нам дан объём шара, ограниченного сферой, то радиус находится так:
где V – это объём шара, число Пи = 3,14.
Способ 3. Альтернативные формулы определения радиуса сферы
В случае, если наша сфера вписана в правильный многогранник или описана вокруг него, можно воспользоваться следующим рядом формул.
Формула 1. Сфера вписана в правильный тетраэдр
Для сферы, которая вписана в правильный тетраэдр:
где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).
Формула 2. Сфера описана около правильного тетраэдра
Для сферы, которая описана около правильного тетраэдра:
где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).
Формула 3. Сфера вписана в куб
Для сферы, которая вписана в куб:
где a – длина ребра куба.
Формула 4. Сфера описана около куба
Для сферы, которая описана около куба:
где a – длина ребра куба.
Загрузить PDF
Загрузить PDF
Радиус шара (обозначается как r или R) – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Как и в случае круга, радиус шара является важной величиной, которая необходима для нахождения диаметра шара, длины окружности, площади поверхности и/или объема. Но радиус шара можно найти и по данному значению диаметра, длины окружности и другой величины. Используйте формулу, в которую можно подставить данные значения.
-
1
Вычислите радиус по диаметру. Радиус равен половине диаметра, поэтому используйте формулу г = D/2. Эта такая же формула, которая используется при вычислении радиуса и диаметра круга.[1]
- Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см. Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).
-
2
Вычислите радиус по длине окружности. Используйте формулу: r = C/2π. Так как длина окружности C = πD = 2πr, то разделите формулу для вычисления длины окружности на 2π и получите формулу для нахождения радиуса.[2]
- Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см.
- Такая же формула используется при вычислении радиуса и длины окружности круга.
-
3
Вычислите радиус по объему шара. Используйте формулу: r = ((V/π)(3/4))1/3.[3]
Объем шара вычисляется по формуле V = (4/3)πr3. Обособив r на одной стороне уравнения, вы получите формулу ((V/π)(3/4))3 = г, то есть для вычисления радиуса объем шара делим на π, результат умножаем на 3/4, а полученный результат возводим в степень 1/3 (или извлекаем кубический корень).[4]
- Например, дан шар с объемом 100 см3. Радиус этого шара вычисляется так:
- ((V/π)(3/4))1/3 = r
- ((100/π)(3/4))1/3 = r
- ((31,83)(3/4))1/3 = r
- (23,87)1/3 = r
- 2,88 см = r
- Например, дан шар с объемом 100 см3. Радиус этого шара вычисляется так:
-
4
Вычислите радиус по площади поверхности. Используйте формулу: г = √(A/(4 π)). Площадь поверхности шара вычисляется по формуле А = 4πr2. Обособив r на одной стороне уравнения, вы получите формулу √(A/(4π)) = r, то есть, чтобы вычислить радиус, нужно извлечь квадратный корень из площади поверхности, деленной на 4π. Вместо того чтобы извлекать корень, выражение (A/(4π)) можно возвести в степень 1/2.[5]
- Например, дан шар с площадью поверхности 1200 см3. Радиус этого шара вычисляется так:
- √(A/(4π)) = r
- √(1200/(4π)) = r
- √(300/(π)) = r
- √(95,49) = r
- 9,77 см = r
Реклама
- Например, дан шар с площадью поверхности 1200 см3. Радиус этого шара вычисляется так:
-
1
Запомните основные величины, которые имеют отношение к вычислению радиуса шара. Радиус шара – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Радиус шара можно вычислить по данным значениям диаметра, длины окружности, объема или площади поверхности.
- Диаметр (D) – это отрезок, который соединяет две точки на поверхности шара и проходит через его центр (то есть это наибольшее расстояние между противоположными точками, лежащими на поверхности шара). Диаметр равен удвоенному радиусу.
- Длина окружности (С) представляет собой длину окружности большого круга, то есть круга, который образует секущая плоскость, проходящая через центр шара.
-
Объем (V) – это значение трехмерного пространства, занимаемого шаром.[6]
- Площадь поверхности (А) – это значение двумерного (плоского) пространства, ограниченного поверхностью шара.
- Пи (π) – это постоянная, которая равна отношению длины окружности к ее диаметру. Первыми десятью цифрами этой постоянной являются 3,141592653, но зачастую число Пи округляется до 3,14.
-
2
Воспользуйтесь значениями данных величин, чтобы найти радиус. Радиус можно вычислить по данным значениям диаметра, длины окружности, объема и площади поверхности. Более того, указанные величины можно найти по данному значению радиуса. Чтобы вычислить радиус, просто преобразуйте формулы для нахождения указанных величин. Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.
- D = 2г. Как и в случае круга, диаметр шара в два раза больше его радиуса.
- C = πD = 2πr. Как и в случае круга, длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара.
-
V = (4/3)πr3. Объем шара равен произведению 4/3 на π и на радиус в кубе.[7]
- А = 4πr2. Площадь поверхности шара равна учетверенному произведению π на радиус в квадрате. Так как площадь круга равна πr2, то площадь поверхности шара в четыре раза больше площади круга, который образует секущая плоскость, проходящая через центр шара.
Реклама
-
1
Найдите координаты (х,у,z) центра шара. Радиус шара равен расстоянию между его центром и любой точкой, лежащей на поверхности шара. Если известны координаты центра шара и любой точки, лежащей на его поверхности, можно найти радиус шара по специальной формуле, вычислив расстояние между двумя точками. Сначала найдите координаты центра шара. Имейте в виду, что так как шар является трехмерной фигурой, то точка будет иметь три координаты (х,у,z), а не две (х,у).
- Рассмотрим пример. Дан шар с центром с координатами (4,-1,12). Воспользуйтесь этими координатами, чтобы найти радиус шара.
-
2
Найдите координаты точки, лежащей на поверхности шара. Теперь нужно найти координаты (х,у,z) любой точки, лежащей на поверхности шара. Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку.
- В нашем примере допустим, что некоторая точка, лежащая на поверхности шара, имеет координаты (3,3,0). Вычислив расстояние между этой точкой и центром шара, вы найдете радиус.
-
3
Вычислите радиус по формуле d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2). Узнав координаты центра шара и точки, лежащей на его поверхности, вы можете найти расстояние между ними, которое равно радиусу шара. Расстояние между двумя точками вычисляется по формуле d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2), где d – расстояние между точками, (x1,y1,z1) – координаты центра шара, (x2,y2,z2) – координаты точки, лежащей на поверхности шара.
- В рассматриваемом примере вместо (x1,y1,z1) подставьте (4,-1,12), а вместо (x2,y2,z2) подставьте (3,3,0):
- d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2)
- d = √((3 – 4)2 + (3 – -1)2 + (0 – 12)2)
- d = √((-1)2 + (4)2 + (-12)2)
- d = √(1 + 16 + 144)
- d = √(161)
- d = 12,69. Это искомый радиус шара.
- В рассматриваемом примере вместо (x1,y1,z1) подставьте (4,-1,12), а вместо (x2,y2,z2) подставьте (3,3,0):
-
4
Имейте в виду, что в общих случаях r = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2). Все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара. Если в формуле для нахождения расстояния между двумя точками “d” заменить на “r”, получится формула для вычисления радиуса шара по известным координатам (x1,y1,z1) центра шара и координатам (x2,y2,z2) любой точки, лежащей на поверхности шара.
- Возведите обе стороны этого уравнения в квадрат, и получите r2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2. Отметьте, что это уравнение соответствует уравнению сферы r2 = x2 + y2 + z2 с центром с координатами (0,0,0).
Реклама
Советы
- Не забывайте про порядок выполнения математических операций. Если вы не помните этот порядок, а ваш калькулятор умеет работать с круглыми скобками, пользуйтесь ими.
- В этой статье рассказывается о вычислении радиуса шара. Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.
- π (Пи) – это буква греческого алфавита, которая обозначает постоянную, равную отношению диаметра круга к длине его окружности. Число Пи является иррациональным числом, которое не записывается как отношение действительных чисел. Существует множество приближений, например, отношение 333/106 позволит найти число Пи с точностью до четырех цифр после десятичной запятой. Как правило, пользуются приблизительным значением числа Пи, которое равно 3,14.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 114 674 раза.
Была ли эта статья полезной?
Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).
Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.
Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.
Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.
В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.
Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.
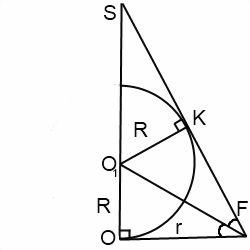
Прямоугольные треугольники OO1F и KO1F равны (по катетам и гипотенузе). Отсюда KF=OF=r.
Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что
![[frac{{OF}}{{K{O_1}}} = frac{{SO}}{{SK}}, Rightarrow frac{r}{R} = frac{H}{{l - r}}.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-2bbdee676e5a28a8736d40625b15ca80_l3.png "Rendered by QuickLaTeX.com")
В треугольнике SOF применим свойство биссектрисы треугольника:
![[frac{{SF}}{{S{O_1}}} = frac{{OF}}{{O{O_1}}}, Rightarrow frac{l}{{H - R}} = frac{r}{R}.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-f689e568a5d867c7d393ae927a8a9876_l3.png "Rendered by QuickLaTeX.com")
Из прямоугольного треугольника OO1F
![[tgangle OF{O_1} = frac{{O{O_1}}}{{OF}} = frac{R}{r}.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-6099a16664ff2208a8b3b5cf6b824644_l3.png "Rendered by QuickLaTeX.com")
При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.
![[frac{l}{{H - R}} = frac{r}{R}, Rightarrow Rl = (H - R)r, Rightarrow ]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-5224ea99ae9b7cc5999e0e2da56bb686_l3.png "Rendered by QuickLaTeX.com")
![[Rl = Hr - Rr, Rightarrow Hr = R(l + r), Rightarrow ]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-671f7bd51bd686f97aac6360e57a3a16_l3.png "Rendered by QuickLaTeX.com")
![[R = frac{{rH}}{{l + r}}.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-56ff18eb278336b48b906e1f2e91e9d3_l3.png "Rendered by QuickLaTeX.com")
Теперь найдем отношение объема пирамиды к площади ее поверхности:
![[frac{V}{{{S_{n.n/}}}} = frac{{frac{1}{3}{S_{ocn}} cdot H}}{{{S_{ocn}} + {S_{bok}}}} = frac{1}{3} cdot frac{{prH}}{{pr + pl}} = ]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-3540cf3c2c95f267fed2949d74d31b95_l3.png "Rendered by QuickLaTeX.com")
![[ = frac{1}{3} cdot frac{{rH}}{{r + l}} = frac{1}{3}R.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-9076a7ad30f3abc80580413c2c8adb68_l3.png "Rendered by QuickLaTeX.com")
Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:
![[R = frac{{3V}}{{{S_{n.n.}}}}.]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-db3578c5738365ed79044df8bfdceff6_l3.png "Rendered by QuickLaTeX.com")
Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны).
