Как найти радиус вписанной окружности формулы - Сайт, где вы сможете решить свои вопросы

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

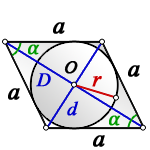
a – сторона ромба

D – большая диагональ

d – меньшая диагональ

α – острый угол

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

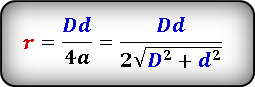
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

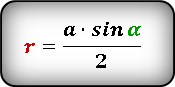
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

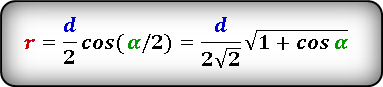
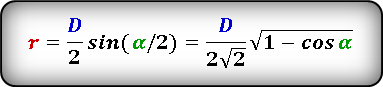
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

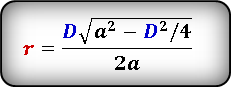
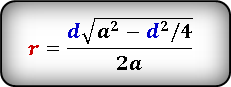
2. Радиус вписанной окружности ромба, равен половине его высоты

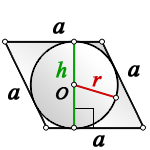
a – сторона ромба

h – высота

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Источник

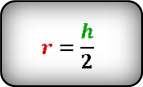
Вписанная окружность — в какую фигуру нельзя вписать

Для решения геометрических задач можно использовать различные формулы и приемы, которые помогут облегчить поиск искомых показателей. Один из способов найти различные неизвестные в многогранной фигуре – сделать это через вписанную окружность.

Вписанная окружность — окружность, которая лежит внутри угла и касается его сторон. Касание происходит в одной точке с каждой стороны.

Вписанная в фигуру окружность, например, в треугольник или многоугольник, будет касаться всех его сторон. Это главное свойство окружности, которая будет называться вписанной. Сама фигура в таком случае называется описанной вокруг окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Следствие

Из этого следует, что вписанная окружность не будет таковой, если не будет касаться всех сторон фигуры.

Окружность точно можно вписать в следующие геометрические фигуры:

треугольник;
выпуклый правильный многоугольник;
квадрат;
равнобедренная трапеция;
ромб.

При этом окружность в данные фигуры может быть вписана лишь единожды.

Четырехугольник является неоднозначной фигурой при процессе вписывания в нее окружности. Для того, чтобы окружность была вписанной в четырехугольник, суммы длин его противоположных сторон должны быть равны.

Окружность точно нельзя вписать в следующие геометрические фигуры:

прямоугольник;
параллелограмм (если он не является ромбом).

Ни один из видов данных фигур не сможет иметь вписанную окружность, так как она не сможет соприкасаться со всеми их сторонами, что является главным признаком вписанной окружности.

Теорема о вписанной окружности

Теорема о вписанной окружности гласит, что в любой треугольник и в любой выпуклый многоугольник и четырехугольник с равными суммами длин противоположных сторон можно вписать окружность, но только одну.

Правило о центре вписанной окружности

Центр окружности при этом будет находиться в точке пересечения биссектрис фигуры. Чтобы определить центр, нужно построить биссектрисы из каждого угла и найти пересечение.

Формула нахождения радиуса вписанной окружности

Вычисление радиуса вписанной окружности ведется по формулам, которые зависят от фигуры и известных данных. Главным условием является тот факт, что фигура должна подходить под список тех, в которые можно вписать окружность.

Радиус — перпендикуляр, соединяющий центр окружности с любой точкой, лежащей на окружности. По длине радиус составляет половину диаметра.

Треугольник

Формула нахождения радиуса окружности, вписанной в треугольник через все стороны:

(r=sqrt{frac{left(p-aright)left(p-bright)left(p-cright)}p},)

где r — радиус,

a, b и c — стороны треугольника,

p — полупериметр, (p=frac{a+b+c}2.)

Формула нахождения радиуса окружности, вписанной в треугольник через сторону и высоту:

(r=frac{btimes h}{b+sqrt{4times h^2+b^2}},)

(r=frac{htimessqrt{a^2-h^2}}{a+sqrt{a^2-h^2}},)

где r — радиус,

a и b — стороны треугольника,

h — высота.

Равносторонний треугольник

Формула нахождения радиуса окружности, вписанной в равносторонний треугольник:

(r=frac a{2sqrt3},)

где r — радиус,

a — сторона треугольника.

Равнобедренный треугольник

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через значения сторон:

(r=frac b2sqrt{frac{2a-b}{2a+b}},)

где r — радиус,

a и b — стороны треугольника.

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через сторону и угол:

(r=Atimesfrac{sinleft(aright)timescosleft(aright)}{1+cosleft(aright)}= Atimescosleft(aright)timestanleft(frac a2right),)

(r=frac b2timesfrac{sinleft(aright)}{1+cosleft(aright)}=frac b2timestanleft(frac a2right),)

где r — радиус,

A и b — стороны треугольника,

a — угол при основании.

Прямоугольный треугольник

Формула нахождения радиуса окружности, вписанной в прямоугольный треугольник:

(r=frac{atimes b}{a+b+c}=frac{a+b-c}2,)

где r — радиус,

a и b — катеты треугольника,

c — гипотенуза.

Равнобедренная трапеция

Формула нахождения радиуса окружности, вписанной в равнобедренную трапецию:

(r=frac h2=frac{sqrt{ctimes b}}2,)

где r — радиус,

с — нижнее основание,

b — верхнее,

а — боковые стороны,

h — высота.

Квадрат

Формула нахождения радиуса окружности, вписанной в квадрат:

(r=frac a2,)

где r — радиус,

а — сторона квадрата.

Ромб

Формула нахождения радиуса окружности, вписанной в ромб через значения диагоналей:

(r=frac{Dtimes d}{4times a}=frac{Dtimes d}{2sqrt{D^2+d^2}}.)

Формула нахождения радиуса окружности, вписанной в ромб через значения стороны и угла:

(r=frac{atimessinleft(aright)}2.)

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и угол:

(r=frac d2timescosleft(frac a2right)=frac d{2sqrt2}timessqrt{1+cosleft(aright)},)

(r=frac D2timessinleft(frac a2right)=frac D{2sqrt2}timessqrt{1-cosleft(aright)}.)

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и сторону:

(r=frac{Dsqrt{a^2-{displaystylefrac{D^2}4}}}{2a},)

(r=frac{dsqrt{a^2-{displaystylefrac{d^2}4}}}{2a}.)

Формула нахождения радиуса окружности, вписанной в ромб через высоту:

(r=frac h2,)

где r — радиус,

а — сторона ромба,

D — большая диагональ,

d — меньшая диагональ,

a — острый угол,

h — высота.

Многоугольник

Формула нахождения радиуса окружности, вписанной в правильный многоугольник:

(r=frac a{2timestanleft({displaystylefrac{180^circ}N}right)},)

где r — радиус,

N — количество сторон многоугольника.

Шестиугольник

Формула нахождения радиуса окружности, вписанной в шестиугольник:

(r=frac{sqrt3}2times a,)

где r — радиус,

a — сторона шестиугольника.

Источник

Удобно, когда все формулы, по которым можно найти радиус вписанной в треугольник и в многоугольник окружности, размещены на одной странице.

Радиус вписанной в многоугольник окружности

Если в многоугольник можно вписать окружность, то формула для вычисления радиуса вписанной окружности:

$[r = frac{S}{p},]$

где p — полупериметр, то есть полусумма длин всех сторон этого многоугольника.

Например, для пятиугольника со сторонами a, b, c, d, e радиус вписанной окружности находится по формуле

$[r = frac{S}{p},]$

$[p = frac{{a + b + c + d + e}}{2},]$

откуда

$[r = frac{{2S}}{{a + b + c + d + e}}.]$

По этой же формуле ищут радиус вписанной в треугольник окружности.

Радиус вписанной в треугольник окружности

Формула для нахождения радиуса вписанной в треугольник окружности (верна для треугольника любого вида)

$[r = frac{S}{p},]$

где p — полупериметр,

$[p = frac{{a + b + c}}{2},]$

где a, b, c — стороны треугольника.

Радиус вписанной в прямоугольный треугольник окружности

Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник

$[r = frac{{a + b - c}}{2},]$

где a и b — катеты, c — гипотенуза.

Радиус окружности, вписанной в правильный многоугольник

Формула радиуса вписанной в правильный многоугольник окружности

$[r = frac{a}{{2tgfrac{{{{180}^o}}}{n}}},]$

где a — сторона многоугольника, n — количество сторон.

Частные случаи — правильный (равносторонний) треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник.

Радиус окружности, вписанной в правильный треугольник

Формула радиуса вписанной окружности для правильного треугольника:

$[r = frac{a}{{2sqrt 3 }}]$

В правильном треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности:

$[r = frac{R}{2}.]$

Радиус окружности, вписанной в квадрат

Формула радиуса вписанной в квадрат окружности:

$[r = frac{a}{2},]$

где a — сторона квадрата.

Радиус окружности, вписанной в правильный шестиугольник

Формула радиуса вписанной в правильный шестиугольник окружности:

$[r = frac{{asqrt 3 }}{2},]$

где a — сторона правильного шестиугольника.

Для любого многоугольника центр вписанной окружности лежит в точке пересечения его биссектрис.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 февраля 2023 года; проверки требуют 2 правки.

Окружность, вписанная в многоугольник ABCDE

Окружность называют вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех его сторон.

В многоугольнике[править | править код]

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех внутренних углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.

$r={frac {S}{p}}$

В треугольнике[править | править код]

Окружность, вписанная в треугольник со сторонами a, b, c.

Свойства вписанной окружности:

$r={sqrt {frac {(-a+b+c)(a-b+c)(a+b-c)}{4(a+b+c)}}};$

${frac {1}{r}}={frac {1}{h_{a}}}+{frac {1}{h_{b}}}+{frac {1}{h_{c}}}$

где a,b,c — стороны треугольника, $h_{a},h_{b},h_{c}$ — высоты, проведённые к соответствующим сторонам^[1];

$r={frac {S}{p}}={sqrt {{frac {(p-a)(p-b)(p-c)}{p}}}}$

где

— площадь треугольника, а

— его полупериметр.

${displaystyle r={frac {p-a}{operatorname {ctg} (alpha /2)}}={frac {p-b}{operatorname {ctg} (beta /2)}}={frac {p-c}{operatorname {ctg} (gamma /2)}}}$

— полупериметр треугольника (Теорема котангенсов).

${displaystyle |OI|^{2}={frac {a,b,c,}{a+b+c}}left[{frac {a,b,c,}{(a+b-c),(a-b+c),(-a+b+c)}}-1right]}$

Если прямая, проходящая через точку I параллельно стороне , пересекает стороны и в точках $A_{1}$ и , то $A_{1}B_{1}=A_{1}B+AB_{1}$ .
Если точки касания вписанной в треугольник окружности соединить отрезками с его сторонами, то получится треугольник $T_{1}$ со свойствами:
- Биссектрисы T являются серединными перпендикулярами T₁
- Пусть T₂ — ортотреугольник T₁. Тогда его стороны параллельны сторонам исходного треугольника T.
- Пусть T₃ — серединный треугольник T₁. Тогда биссектрисы T являются высотами T₃.
- Пусть T₄ — ортотреугольник T₃, тогда биссектрисы T являются биссектрисами T₄.
Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен ${displaystyle {frac {a+b-c}{2}}={frac {ab}{a+b+c}}}$ .
Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно $d={frac {a+b-c}{2}}=p-c$ .
Расстояние от вершины C до центра вписанной окружности равно $l_{c}={frac {r}{sin({frac {gamma }{2}})}}$ , где — радиус вписанной окружности, а γ — угол вершины C.
Расстояние от вершины C до центра вписанной окружности может также быть найдено по формулам $l_{c}={sqrt {(p-c)^{2}+r^{2}}}$ и $l_{c}={sqrt {ab-4Rr}}$
Теорема о трезубце или теорема трилистника: Если D — точка пересечения биссектрисы угла A с описанной окружностью треугольника ABC, I и J — соответственно центры вписанной и вневписанной окружности, касающейся стороны BC, тогда .

Полувписанная окружность и центр гомотетии G для вписанной и описанной окружностей с радиусами соответственно r и R. Лемма Веррьера: Центр вписанной окружности лежит на отрезке, соединяющем точки касания сторон треугольника и окружности Веррьера (полувписанной окружности)

Теорема Фейербаха. Окружность девяти точек касается всех трёх вневписанных окружностей, а также вписанной окружности. Точка касания окружности Эйлера и вписанной окружности известна как точка Фейербаха.

Связь вписанной и описанной окружностей[править | править код]

${displaystyle {frac {r}{R}}={frac {4S^{2}}{pabc}}=cos alpha +cos beta +cos gamma -1;}$

^[4]

$2Rr={frac {abc}{a+b+c}}$

${frac {r}{R}}=4sin {frac {alpha }{2}}sin {frac {beta }{2}}sin {frac {gamma }{2}}=cos alpha +cos beta +cos gamma -1$

где — полупериметр треугольника, — его площадь.

Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности^[5].

Для треугольника можно построить полувписанную окружность, или окружность Варьера. Это окружность, касающаяся двух сторон треугольника и его описанной окружности внутренним образом. Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке. Эта точка служит центром гомотетии с положительным коэффициентом, переводящей описанную окружность во вписанную.
Центр вписанной окружности лежит на отрезке, соединяющем точки касания сторон треугольника и полувписанной окружности.

Полувписанная окружность и центр гомотетии G для вписанной и описанной окружностей с радиусами соответственно r и R

Связь центра вписанной окружности и середин высот треугольника[править | править код]

Теорема Ригби. Если к любой стороне остроугольного треугольника провести высоту и касающуюся ее с другой стороны вневписанную окружность, то точка касания последней с этой стороной, середина упомянутой высоты, а также инцентр лежат на одной прямой.^[6].
Из теоремы Ригби следует, что 3 отрезка, соединяющих середину каждой из 3 высот треугольника с точкой касания вневписанной окружности, проведенной к той же стороне, что и высота, пересекаются в инцентре.

В четырёхугольнике[править | править код]

Описанный четырёхугольник, если у него нет самопересечений («простой»), должен быть выпуклым.
Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
Иными словами, в выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны: .

Во всяком описанном четырёхугольнике две середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона). На ней же лежит середина отрезка с концами в точках пересечения продолжений противоположных сторон четырёхугольника (если они не параллельны). Эта прямая называется прямой Ньютона. На рисунке она зелёная, диагонали красные, отрезок с концами в точках пересечения продолжений противоположных сторон четырёхугольника тоже красный.
Центр описанной около четырёхугольника окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара).

В сферическом треугольнике[править | править код]

Вписанная окружность для сферического треугольника — это окружность, касающаяся всех его сторон.

Тангенс радиуса^[7] вписанной в сферический треугольник окружности равен^[8]^:73-74

${displaystyle operatorname {tg} r={sqrt {frac {sin(p-a)sin(p-b)sin(p-c)}{sin p}}}}$

Вписанная в сферический треугольник окружность принадлежит сфере. Радиус, проведенный из центра сферы через центр вписанной окружности пересечет сферу в точке пересечения биссектрис углов (дуг больших кругов сферы, делящих углы пополам) сферического треугольника^[8]^:20-21.

Обобщения[править | править код]

Вписанной сферой называется сфера, касающаяся всех граней многогранника.
Эллипс Штейнера — вписанный в треугольник эллипс.

См. также[править | править код]

Вневписанная окружность
Внеописанный четырёхугольник
Вписанная и вневписанные в треугольник окружности
Вписанные и описанные фигуры для треугольника
Замечательные прямые треугольника
Замечательные точки треугольника
Вписанное коническое сечение^[en]
Описанная окружность
Описанный четырёхугольник
Ортоцентр
Степень точки относительно окружности
Теорема Мансиона
Теорема о трезубце
Теорема Тебо 2 и 3
Теорема Фейербаха
Теорема Харкорта
Точки Аполлония
Треугольник
Центроид
Центроид треугольника

Примечания[править | править код]

↑ Altshiller-Court, 1925, p. 79.
↑ Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — С. 130. — 334 с. Архивная копия от 4 марта 2016 на Wayback Machine
↑ Ефремов Д. Новая геометрия треугольника. Изд. 2. Серия: Физико-математическое наследие (репринтное воспроизведение издания).. — Москва: Ленанд, 2015. — 352 с. — ISBN 978-5-9710-2186-5. Архивная копия от 22 июля 2020 на Wayback Machine
↑ Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.
↑ Мякишев А. Г. Элементы геометрии треугольника. Серия: «Библиотека „Математическое просвещение“». М.: МЦНМО, 2002. c. 11, п. 5
↑ Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: The Mathematical Association of America, 1996, ISBN 978-0883856390. p. 30, Figure 34, §3. An Unlikely Collinearity.
↑ Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведенного из центра сферы через центр окружности, со сферой и точку касания окружностью стороны треугольника.
↑ ¹ ² Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.

Литература[править | править код]

Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 89. — 383 с. — ISBN 5-09-001287-3.
Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 52-53. — ISBN 5-94057-170-0.
Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Примеры задач

Формулы вычисления радиуса вписанной окружности

Произвольный треугольник

Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.