Как найти радиус вписанной окружности многоугольника формула

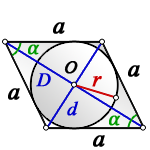
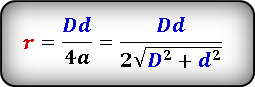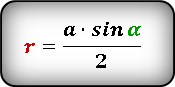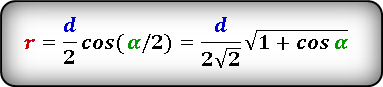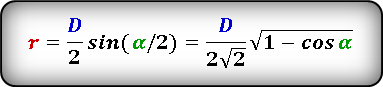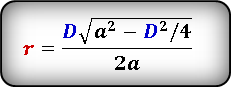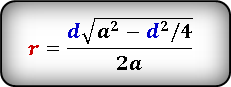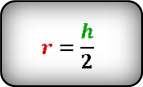1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

a – сторона ромба

D – большая диагональ

d – меньшая диагональ

α – острый угол

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

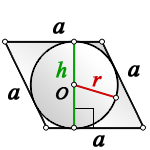
2. Радиус вписанной окружности ромба, равен половине его высоты

a – сторона ромба

h – высота

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Удобно, когда все формулы, по которым можно найти радиус вписанной в треугольник и в многоугольник окружности, размещены на одной странице.

Радиус вписанной в многоугольник окружности

Если в многоугольник можно вписать окружность, то формула для вычисления радиуса вписанной окружности:

   

где p — полупериметр, то есть полусумма длин всех сторон этого многоугольника.

Например, для пятиугольника со сторонами a, b, c, d, e радиус вписанной окружности находится по формуле

   

   

откуда

   

По этой же формуле ищут радиус вписанной в треугольник окружности.

Радиус вписанной в треугольник окружности

Формула для нахождения радиуса вписанной в треугольник окружности (верна для треугольника любого вида)

   

где p — полупериметр,

   

где a, b, c — стороны треугольника.

Радиус вписанной в прямоугольный треугольник окружности

Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник

   

где a и b — катеты, c — гипотенуза.

Радиус окружности, вписанной в правильный многоугольник

Формула радиуса вписанной в правильный многоугольник окружности

   

где a — сторона многоугольника, n — количество сторон.

Частные случаи — правильный (равносторонний) треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник.

Радиус окружности, вписанной в правильный треугольник

Формула радиуса вписанной окружности для правильного треугольника:

   

В правильном треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности:

   

Радиус окружности, вписанной в квадрат

Формула радиуса вписанной в квадрат окружности:

   

где a — сторона квадрата.

Радиус окружности, вписанной в правильный шестиугольник

Формула радиуса вписанной в правильный шестиугольник окружности:

   

где a — сторона правильного шестиугольника.

Для любого многоугольника центр вписанной окружности лежит в точке пересечения его биссектрис.

Вписанная окружность — в какую фигуру нельзя вписать

Для решения геометрических задач можно использовать различные формулы и приемы, которые помогут облегчить поиск искомых показателей. Один из способов найти различные неизвестные в многогранной фигуре – сделать это через вписанную окружность.

Вписанная окружность — окружность, которая лежит внутри угла и касается его сторон. Касание происходит в одной точке с каждой стороны. 

Вписанная в фигуру окружность, например, в треугольник или многоугольник, будет касаться всех его сторон. Это главное свойство окружности, которая будет называться вписанной. Сама фигура в таком случае называется описанной вокруг окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Окружность точно можно вписать в следующие геометрические фигуры:

• треугольник;
• выпуклый правильный многоугольник;
• квадрат;
• равнобедренная трапеция;
• ромб.

При этом окружность в данные фигуры может быть вписана лишь единожды.

Четырехугольник является неоднозначной фигурой при процессе вписывания в нее окружности. Для того, чтобы окружность была вписанной в четырехугольник, суммы длин его противоположных сторон должны быть равны.

Окружность точно нельзя вписать в следующие геометрические фигуры:

• прямоугольник;
• параллелограмм (если он не является ромбом).

Ни один из видов данных фигур не сможет иметь вписанную окружность, так как она не сможет соприкасаться со всеми их сторонами, что является главным признаком вписанной окружности.

Теорема о вписанной окружности

Теорема о вписанной окружности гласит, что в любой треугольник и в любой выпуклый многоугольник и четырехугольник с равными суммами длин противоположных сторон можно вписать окружность, но только одну.

Правило о центре вписанной окружности

Центр окружности при этом будет находиться в точке пересечения биссектрис фигуры. Чтобы определить центр, нужно построить биссектрисы из каждого угла и найти пересечение.

Формула нахождения радиуса вписанной окружности

Вычисление радиуса вписанной окружности ведется по формулам, которые зависят от фигуры и известных данных. Главным условием является тот факт, что фигура должна подходить под список тех, в которые можно вписать окружность.

Радиус — перпендикуляр, соединяющий центр окружности с любой точкой, лежащей на окружности. По длине радиус составляет половину диаметра.

Треугольник

Формула нахождения радиуса окружности, вписанной в треугольник через все стороны:

(r=sqrt{frac{left(p-aright)left(p-bright)left(p-cright)}p},)

где r — радиус,

a, b и c — стороны треугольника,

p — полупериметр, (p=frac{a+b+c}2.)

Формула нахождения радиуса окружности, вписанной в треугольник через сторону и высоту:

(r=frac{btimes h}{b+sqrt{4times h^2+b^2}},)

(r=frac{htimessqrt{a^2-h^2}}{a+sqrt{a^2-h^2}},)

где r — радиус,

a и b — стороны треугольника,

h — высота.

Равносторонний треугольник

Формула нахождения радиуса окружности, вписанной в равносторонний треугольник:

(r=frac a{2sqrt3},)

где r — радиус,

a — сторона треугольника.

Равнобедренный треугольник

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через значения сторон:

(r=frac b2sqrt{frac{2a-b}{2a+b}},)

где r — радиус,

a и b — стороны треугольника.

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через сторону и угол:

(r=Atimesfrac{sinleft(aright)timescosleft(aright)}{1+cosleft(aright)}= Atimescosleft(aright)timestanleft(frac a2right),)

(r=frac b2timesfrac{sinleft(aright)}{1+cosleft(aright)}=frac b2timestanleft(frac a2right),)

где r — радиус,

A и b — стороны треугольника,

a — угол при основании.

Прямоугольный треугольник

Формула нахождения радиуса окружности, вписанной в прямоугольный треугольник:

(r=frac{atimes b}{a+b+c}=frac{a+b-c}2,)

где r — радиус,

a и b — катеты треугольника,

c — гипотенуза.

Равнобедренная трапеция

Формула нахождения радиуса окружности, вписанной в равнобедренную трапецию:

(r=frac h2=frac{sqrt{ctimes b}}2,)

где r — радиус,

с — нижнее основание,

b — верхнее,

а — боковые стороны,

h — высота.

Квадрат

Формула нахождения радиуса окружности, вписанной в квадрат:

(r=frac a2,)

где r — радиус,

а — сторона квадрата.

Ромб

Формула нахождения радиуса окружности, вписанной в ромб через значения диагоналей:

(r=frac{Dtimes d}{4times a}=frac{Dtimes d}{2sqrt{D^2+d^2}}.)

Формула нахождения радиуса окружности, вписанной в ромб через значения стороны и угла:

(r=frac{atimessinleft(aright)}2.)

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и угол:

(r=frac d2timescosleft(frac a2right)=frac d{2sqrt2}timessqrt{1+cosleft(aright)},)

(r=frac D2timessinleft(frac a2right)=frac D{2sqrt2}timessqrt{1-cosleft(aright)}.)

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и сторону:

(r=frac{Dsqrt{a^2-{displaystylefrac{D^2}4}}}{2a},)

(r=frac{dsqrt{a^2-{displaystylefrac{d^2}4}}}{2a}.)

Формула нахождения радиуса окружности, вписанной в ромб через высоту:

(r=frac h2,)

где r — радиус,

а — сторона ромба,

D — большая диагональ,

d — меньшая диагональ,

a — острый угол,

h — высота.

Многоугольник

Формула нахождения радиуса окружности, вписанной в правильный многоугольник:

(r=frac a{2timestanleft({displaystylefrac{180^circ}N}right)},)

где r — радиус,

N — количество сторон многоугольника.

Шестиугольник

Формула нахождения радиуса окружности, вписанной в шестиугольник:

(r=frac{sqrt3}2times a,)

где r — радиус,

a — сторона шестиугольника.

В публикации представлена формула, с помощью которой можно найти радиус окружности, вписанной в правильный многоугольник, а также приведен пример решения задачи для лучшего понимания представленного материала.

• Формула расчета радиуса окружности

• Пример задачи

Формула расчета радиуса окружности

На рисунке изображен правильный шестиугольник со вписанной в него окружностью, но формула ниже подходит для любого правильного n-угольника.

где a – длина стороны.

Примечание: зная радиус вписанного круга можно найти сторону равностороннего n-угольника:

Пример задачи

Вычислите радиус вписанной в правильный восьмиугольник окружности, если длина его стороны составляет 12 см.

Решение:
Воспользуемся первой формулой, подставив в нее известное значение.

Радиус вписанной окружности

Удобно, когда все формулы, по которым можно найти радиус вписанной в треугольник и в многоугольник окружности, размещены на одной странице.

Радиус вписанной в многоугольник окружности

Если в многоугольник можно вписать окружность, то формула для вычисления радиуса вписанной окружности:

где p — полупериметр, то есть полусумма длин всех сторон этого многоугольника.

Например, для пятиугольника со сторонами a, b, c, d, e радиус вписанной окружности находится по формуле

Радиус вписанной в треугольник окружности

Формула для нахождения радиуса вписанной в треугольник окружности (верна для треугольника любого вида)

где p — полупериметр,

где a, b, c — стороны треугольника.

Радиус вписанной в прямоугольный треугольник окружности

Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник

где a и b — катеты, c — гипотенуза.

Радиус окружности, вписанной в правильный многоугольник

Формула радиуса вписанной в правильный многоугольник окружности

где a — сторона многоугольника, n — количество сторон.

Частные случаи — правильный (равносторонний) треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник.

Радиус окружности, вписанной в правильный треугольник

Формула радиуса вписанной окружности для правильного треугольника:

В правильном треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности:

Радиус окружности, вписанной в квадрат

Формула радиуса вписанной в квадрат окружности:

где a — сторона квадрата.

Радиус окружности, вписанной в правильный шестиугольник

Формула радиуса вписанной в правильный шестиугольник окружности:

где a — сторона правильного шестиугольника.

Для любого многоугольника центр вписанной окружности лежит в точке пересечения его биссектрис.

5 Comments

Почему для квадрата не подходит формула S=pr

Вполне подходит. Полупериметр p=2а, r=a/2, откуда S=2a∙(a/2)=a².

Огромное спасибо этому сайту!Всё просто, понятно и правильно.

Радиус вписанной окружности это есть высота правильного многоугольника? Работает ли это для всех многоугольников?

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a , b , c – стороны треугольника

p – полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a – сторона треугольника

r – радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a – равные стороны равнобедренного треугольника

b – сторона ( основание)

α – угол при основании

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a – равные стороны равнобедренного треугольника

b – сторона ( основание)

h – высота

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

1. Не во всякий четырехугольник можно вписать окружность.
2. Если у четырехугольника суммы длин его противолежащих
   сторон равны, то окружность, может быть, вписана (Теорема Пито).
3. Центр вписанной окружности и середины двух
   диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
4. Точка пересечения биссектрис — это центр вписанной окружности.
5. Точка касания — это точка, в которой соприкасается
   окружность и любая из сторон четырехугольника.
6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

[spoiler title=”источники:”]

http://www-formula.ru/2011-09-24-00-40-48

http://colibrus.ru/vpisannaya-okruzhnost/

[/spoiler]