Радиус вписанной окружности в прямоугольный треугольник
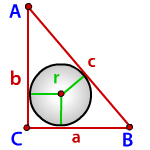
a, b – катеты треугольника
с – гипотенуза
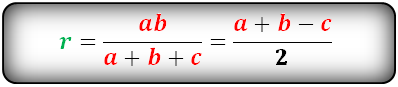
Формула радиуса вписанной окружности в прямоугольный треугольник (r):
Калькулятор – вычислить, найти радиус вписанной окружности в прямоугольный треугольник
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 13 августа 2021
Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
- Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
- Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
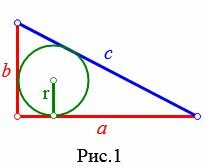
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
где
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
где c вычисляется из теоремы Пифагора:
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
Учитывая (5), формулу (6) можно переписать так:
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
Ответ: 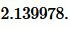
2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
Из теоремы синусов имеем:
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
Тогда из (8) получим:
Далее, из теоремы синусов:
Откуда:
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
или
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
Ответ: 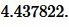
3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
или
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
Ответ: 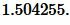
Смотрите также:
- Радиус описанной окружности около треугольника онлайн
- Радиус вписанной в треугольник окружности онлайн
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- Радиус вписанной окружности в равносторонний треугольник онлайн
Утверждение.
Радиус вписанной в прямоугольный треугольник окружности равен
![]()
где a и b — катеты, c — гипотенуза.
Доказательство:
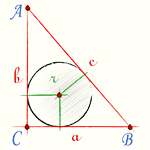
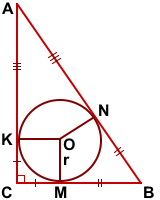 Пусть в прямоугольном треугольнике ABC катеты BC=a, AC=b, гипотенуза AB=c.
Пусть в прямоугольном треугольнике ABC катеты BC=a, AC=b, гипотенуза AB=c.
Проведём радиусы OK, OM, ON к сторонам треугольника.
![]()
(как радиусы, проведённые в точку касания).
![]()
(как отрезки касательных, проведённых из одной точки).
Отсюда следует, что четырёхугольник CKOM — квадрат, стороны которого равны радиусу вписанной в треугольник ABC окружности: CK=CM=OM=OK=r.
Следовательно,
![]()
![]()
![]()
то есть
![]()
Таким образом, формула радиуса вписанной в прямоугольный треугольник окружности
![]()
Что и требовалось доказать.
Радиус вписанной окружности в прямоугольный треугольник
a , b – катеты треугольника
с – гипотенуза
Формула радиуса вписанной окружности в прямоугольный треугольник ( r ):
Калькулятор – вычислить, найти радиус вписанной окружности в прямоугольный треугольник
Нахождение радиуса вписанной в треугольник окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Формулы вычисления радиуса вписанной окружности
Произвольный треугольник
Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.


где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.


где a и b – катеты, c – гипотенуза треугольника.
Равнобедренный треугольник
Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:


где a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:


где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:

Остается только применить соответствующую формулу для вычисления радиуса круга:

Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:
Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
| ( small r= frac<large S><large p>, ) | (1) |
| ( small p= frac<large a+b+c><large 2>. ) | (2) |
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
| ( small S= large frac<1> <2>small cdot a cdot b. ) | (3) |
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
| ( small r= large frac<frac<1><2>ab><frac<1><2>(a+b+c)> ) ( small = large frac, ) | (4) |
| ( small c= sqrt< a^2+b^2>. ) | (5) |
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
| ( small r= frac<large ab(a+b-c)> <large (a+b+c)(a+b-c)>) ( small = frac<large ab(a+b-c)> <large (a+b)^2-c^2>) ( small = frac<large ab(a+b-c)> <large a^2+2ab+b^2-c^2>) | (6) |
Учитывая (5), формулу (6) можно переписать так:
( small r= frac<large ab(a+b-c)> <large 2ab>) ( small = frac<large a+b-c> <large 2>.)
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
| ( small r= frac<large a+b-c> <large 2>,) | (7) |
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
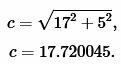
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
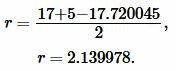
Ответ: 
2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
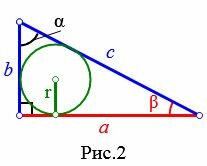
( small frac<large a><large sin alpha>=frac<large b> <large sin beta>.)
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
| ( small frac<large a><large sin alpha>=frac<large a> <large sin (90°-beta)>) ( small =frac<large a><large cos beta>=frac<large b> <large sin beta>.) | (8) |
Тогда из (8) получим:
| ( small b=frac<large a cdot sin beta><large cos beta>. ) | (9) |
Далее, из теоремы синусов:
( small frac<large a><large sin alpha>=frac<large a> <large sin (90°-beta)>) ( small =frac<large a><large cos beta>=frac<large c> <large sin 90°>.)
| ( small c=frac<large a> <large cos beta>.) | (10) |
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
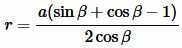 |
(11) |
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
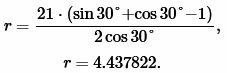
Ответ: 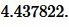
3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
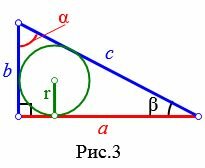
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
( small alpha+beta=90°) ( small beta=90°-alpha )
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
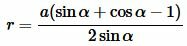 |
(12) |
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
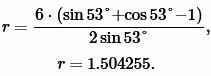
Ответ: 
[spoiler title=”источники:”]
http://matworld.ru/geometry/radius-vpisannoj-okruzhnosti-v-pryamougolnyj-treugolnik.php
[/spoiler]
Радиус вписанной окружности прямоугольного треугольника, формула
Радиус вписанной окружности в прямоугольный треугольник вычисляется по классической формуле
[r = sqrt{frac{(p-a)(p-b)(p-c)}{p}}]
где
[p=frac{1}{2}(a+b+c)]
(a, b, c – стороны треугольника; r – радиус вписанной окружности в треугольник)
сторону c найдем по теореме Пифагора:
[ с = sqrt{a^2+b^2}]
(a, b – стороны прямоугольного треугольника; r – радиус вписанной окружности прямоугольного треугольника)
Вычислить, найти радиус вписанной окружности прямоугольного треугольника по формуле (1)
Радиус вписанной окружности прямоугольного треугольника |
стр. 260 |
|---|
