Радиус вписанной окружности в трапецию
с – нижнее основание
b – верхнее основание
a – боковые стороны
h – высота
Формула радиуса вписанной окружности равнобочной трапеции ( r ):
Калькулятор – вычислить, найти радиус вписанной окружности в равнобочную трапецию
Радиус вписанной окружности в трапецию, формула
Радиус вписанной окружности в трапецию равен половине высоты трапеции.
Главное чтобы выполнялось условие при котором в данную трапецию возможно вписать окружность. В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.:
Иначе в данную трапецию нельзя вписать окружность.
бедро трапеции выражается через высоту по теореме Пифагора:
Отсюда — зная все стороны трапеции вычислим такую высоту трапеции, которая удовлетворяет условию вписанной окружности (3).
после небольших преобразований получим
используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим
И соответственно радиус вписанной окружности в трапецию
Вписанная в равнобедренную трапецию окружность
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
Если MN —
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
По свойству равнобедренной трапеции,
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
[spoiler title=”источники:”]
http://www.fxyz.ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8/%D0%BF%D0%BB%D0%BE%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D0%B8%D0%B3%D1%83%D1%80%D1%8B/%D0%B2%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%D0%BD%D1%8B%D0%B5_%D0%B8_%D0%BE%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%D0%BD%D1%8B%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B8/%D1%80%D0%B0%D0%B4%D0%B8%D1%83%D1%81_%D0%B2%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%D0%BD%D0%BE%D0%B9_%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D0%B8/%D0%B2_%D1%82%D1%80%D0%B0%D0%BF%D0%B5%D1%86%D0%B8%D1%8E/
[/spoiler]
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
 То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
![]()
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
 Если MN —
Если MN —
средняя линия
трапеции ABCD,
AD||BC, то
![]()
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
 По свойству равнобедренной трапеции,
По свойству равнобедренной трапеции,
![]()
Если AD=a, BC=b,
![]()
![]()
Из прямоугольного треугольника ABF по теореме Пифагора
![]()
![]()
![]()
![]()
![]()
![]()
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
![]()
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

AK=AP=DP=DN,
BK=BF=CF=CN.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.
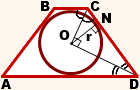 Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
![]()
Значит, треугольник COD — прямоугольный,
![]()
(как радиус, проведенный в точку касания).
Следовательно, ON — высота, проведённая к гипотенузе,
![]()
Радиус вписанной окружности в трапецию
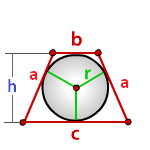
с – нижнее основание
b – верхнее основание
a – боковые стороны
h – высота
Формула радиуса вписанной окружности равнобочной трапеции (r):
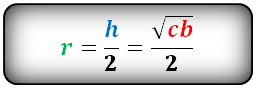
Калькулятор – вычислить, найти радиус вписанной окружности в равнобочную трапецию
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 13 августа 2021
Трапеция является несколько нестандартной фигурой среди четырехугольников. Она не является правильным многоугольником, однако обладает рядом отличительных свойств, среди которых – возможность вписать в равнобокую трапецию окружность. Это обусловлено тем, что для четырехугольников действует правило, согласно которому в него можно вписать окружность, если суммы его противоположных сторон равны. Не каждая трапеция соблюдает это правило, но если в нее все-таки вписана окружность, значит, сумма ее оснований равна сумме боковых сторон. Поскольку радиусы окружности, опущенные на основания трапеции, находятся по отношению к ним под прямым углом, следовательно, они совпадают с высотой трапеции, из чего можно вывести формулу радиуса окружности вписанной в трапецию через высоту:

Так как окружность можно вписать только в трапецию, у которой суммы противоположных сторон равны, то путем нехитрых преобразований через формулы квадрата разности и квадрата суммы можно получить, что высота трапеции равна среднему геометрическому ее оснований a и b.

Следовательно, не зная высоты, можно вычислить радиус окружности, вписанной в трапецию, через основания:

Существует и другой способ найти радиус вписанной в трапецию окружности. Для этого необходимо провести биссектрисы двух углов у боковой стороны. Точка их пересечения должна совпасть с центром вписанной окружности, а также образовать прямой угол. Соответственно, радиус в таком треугольнике станет высотой, которая, исходя из его свойств, равна среднему геометрическому проекций катетов на гипотенузу, то есть боковую сторону трапеции.

Радиус вписанной окружности в трапецию, формула
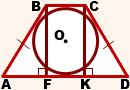
Радиус вписанной окружности в трапецию равен половине высоты трапеции.
[r=frac{h}{2}]
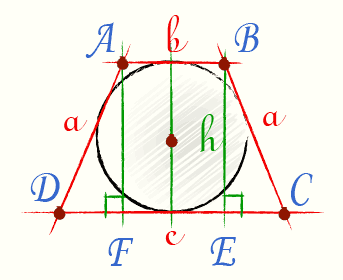
Радиус вписанной окружности в трапецию
Главное чтобы выполнялось условие при котором в данную трапецию возможно вписать окружность.
В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.:
[ AB+DC = AD+BC]
или
[ 2a = b+c]
Иначе в данную трапецию нельзя вписать окружность.
бедро трапеции выражается через высоту по теореме Пифагора:
[ BC = a = sqrt{h^2 + Big(frac{c-b}{2}Big)^2} ]
Отсюда — зная все стороны трапеции вычислим такую высоту трапеции, которая удовлетворяет условию вписанной окружности (3).
[b+c = 2 sqrt{h^2 + Big(frac{c-b}{2}Big)^2}]
после небольших преобразований получим
[h = sqrt{ Big(frac{c+b}{2}Big)^2 – Big(frac{c-b}{2}Big)^2}]
[h = frac{1}{2} sqrt{ (c+b)^2 – (c-b)^2}]
используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим
[h=sqrt{bc}]
И соответственно радиус вписанной окружности в трапецию
[r=frac{h}{2}=frac{sqrt{bc}}{2}]
Вычислить, найти радиус вписанной окружности в трапецию по формуле (1,2,3,4,5)
Радиус вписанной окружности в трапецию |
стр. 259 |
|---|
