Как найти радиус вписаной окружности около треугольника

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

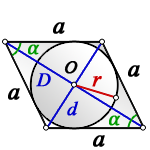
a – сторона ромба

D – большая диагональ

d – меньшая диагональ

α – острый угол

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

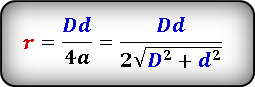
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

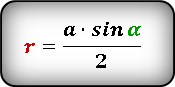
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

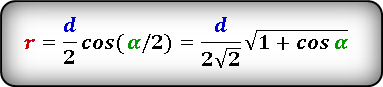
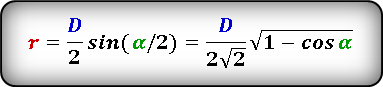
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

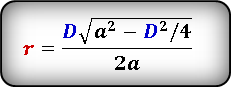
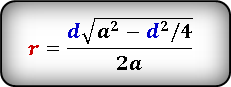
2. Радиус вписанной окружности ромба, равен половине его высоты

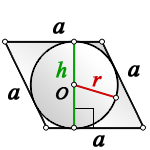
a – сторона ромба

h – высота

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

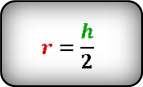
Удобно, когда все формулы, по которым можно найти радиус вписанной в треугольник и в многоугольник окружности, размещены на одной странице.

Радиус вписанной в многоугольник окружности

Если в многоугольник можно вписать окружность, то формула для вычисления радиуса вписанной окружности:

где p — полупериметр, то есть полусумма длин всех сторон этого многоугольника.

Например, для пятиугольника со сторонами a, b, c, d, e радиус вписанной окружности находится по формуле

откуда

По этой же формуле ищут радиус вписанной в треугольник окружности.

Радиус вписанной в треугольник окружности

Формула для нахождения радиуса вписанной в треугольник окружности (верна для треугольника любого вида)

где p — полупериметр,

где a, b, c — стороны треугольника.

Радиус вписанной в прямоугольный треугольник окружности

Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник

где a и b — катеты, c — гипотенуза.

Радиус окружности, вписанной в правильный многоугольник

Формула радиуса вписанной в правильный многоугольник окружности

где a — сторона многоугольника, n — количество сторон.

Частные случаи — правильный (равносторонний) треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник.

Радиус окружности, вписанной в правильный треугольник

Формула радиуса вписанной окружности для правильного треугольника:

В правильном треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности:

Радиус окружности, вписанной в квадрат

Формула радиуса вписанной в квадрат окружности:

где a — сторона квадрата.

Радиус окружности, вписанной в правильный шестиугольник

Формула радиуса вписанной в правильный шестиугольник окружности:

где a — сторона правильного шестиугольника.

Для любого многоугольника центр вписанной окружности лежит в точке пересечения его биссектрис.

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса вписанной окружности

Произвольный треугольник

Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.

где a и b – катеты, c – гипотенуза треугольника.

Равнобедренный треугольник

Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:

где a – боковые стороны, b – основание треугольника.

Равносторонний треугольник

Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.

Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:

Остается только применить соответствующую формулу для вычисления радиуса круга:

Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.

Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:

В любой треугольник можно вписать окружность. Радиус такой окружности будет представлять собой квадратный корень из отношения разности полупериметра с каждой стороной к самому полупериметру.

Если упростить данную формулу для прямоугольного треугольника, воспользовавшись теоремой Пифагора, то мы получим следующее выражение:

Так как в равнобедренном треугольнике боковые стороны равны, то в формуле остаются только обозначения a и b, и ее вид упрощается из все того же первого радикала до следующей формы:

В случае с равносторонним треугольником все еще гораздо проще, и его формула может быть выведена не только из формулы для произвольного треугольника, но также и из свойств высоты-медианы-биссектрисы, которые совпадают и делят любую из сторон на две равные части:

Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.

Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.

Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.

В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.

Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.

Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.

Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.

Всего различают четыре вида треугольников:

• Разносторонний / любой
• Правильный / равносторонний
• Равнобедренный /  равнобочный
• Прямоугольный / прямой

Радиус вписанной окружности в любой треугольник

1. Радиус вписанной окружности в любой треугольник через площадь и полупериметр

   [ r = frac{S}{p} ]

   S — площадь; p — полупериметр;

2. Радиус вписанной окружности в любой треугольник через все стороны и полупериметр

   [ r = sqrtfrac{{(p-a)(p-b)(p-c)}}{p} ]

   a, b, c — стороны; p — полупериметр;
3. Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр

   [ r = frac{frac{1}{2}a cdot h}{p} ]

   a — основание, сторона на которую падает высота; h — высота; p — полупериметр;

4. Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности

   [ r = frac{D}{2} ]

   D — диаметр вписанной окружности;

Радиус вписанной окружности в правильный треугольник

1. Радиус вписанной окружности в правильный треугольник через сторону

   [ r = frac{a}{2sqrt 3} ]

   a — сторона;

2. Радиус вписанной окружности в правильный треугольник через радиус описанной окружности

   [ r = frac{R}{2} ]

   R — радиус описанной окружности;

3. Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности

   [ r = frac{D}{2} ]

   D — диаметр вписанной окружности;

Радиус вписанной окружности в равнобедренный треугольник

1. Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание

   [ r = frac{b}{2} cdot sqrt{frac{2a-b}{2a+b}} ]

   a — боковая сторона; b — основание;

2. Радиус вписанной окружности в равнобедренный треугольник через высоту и основание

   [ r = frac{bh}{b + sqrt{4h^2+b^2}} ]

   b — основание; h — высота;
3. Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности

   [ r = frac{D}{2} ]

   D — диаметр вписанной окружности;

Радиус вписанной окружности в прямоугольный треугольник

1. Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу

   [ r = frac{a+b-c}{2} ]

   a, b — катеты; с — гипотенуза.

2. Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета

   [ r = frac{ab}{a+b+c} ]

   c — гипотенуза; a, b — катеты;

3. Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности

   [ r = frac{D}{2} ]

   D — диаметр вписанной окружности;

   ---

Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.

Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.

Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.

В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.