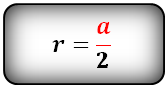В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в квадрат. Также разберем примеры решения задач для закрепления теоретического материала.
-
Формулы вычисления радиуса вписанной окружности
- Через сторону квадрата
- Через диагональ квадрата
-
Примеры задач
Формулы вычисления радиуса вписанной окружности
Через сторону квадрата
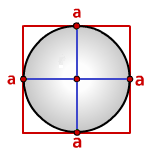
Радиус r вписанной в квадрат окружности равняется половине длины его стороны a.
Через диагональ квадрата
Радиус r вписанной в квадрат окружности равняется длине его диагонали d, деленной на произведение числа 2 и квадратного корня из двух.
Примеры задач
Задание 1
Найдите радиус вписанной в квадрат окружности, если известно, что длина его стороны равняется 7 см.
Решение
Воспользуемся первой формулой, подставив в него известное значение:
Задание 2
Известно, что радиус вписанной в квадрат окружности составляет 12 см. Найдите длину его диагонали.
Решение
Формулу для нахождения диагонали можно вывести из формулы для расчета радиуса круга:
Здравствуйте, уважаемые читатели. Продолжаем разбор заданий с окружностью. В этой статье рассмотрим задачи на вписанную окружность в квадрат и описанную около квадрата.
1. Центральные и вписанные углы.
2.Касательная, хорда, секущая.
3.Вписанная и описанная окружность (треугольник)
4. Вписанная и описанная окружность (квадрат)
Все задачи такого типа достаточно простые. Приступим сразу же к решению задач.
Задача №1
Решение:
Радиус окружности – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
Решение к этой задачи представлю в виде картинки.
О – центр окружности, r – радиус окружности. В этой задаче радиус окружности равен половине стороны квадрата. Ответ 8.
Задача №2
Найдите площадь квадрата, описанного вокруг окружности радиуса 9
Решение:
Задача обратная той, что мы решили выше. Так как радиус окружности равен 9, то сторона квадрата равна 18. Площадь квадрата равна:
Задача №3
Решение:
В предыдущих задачах мы определили, что если известен радиус вписанной окружности в квадрат, то сторона квадрата будет равна удвоенному значению радиуса.
Зная сторону квадрата, диагональ квадрата найдем, используя теорему Пифагора.
Задача №4
Решение:
Эта задача, включает в себя все этапы, которые были разобраны выше. Задачу можно разбить на действия:
1) Найдем сторону квадрата.
2) Найдем диагональ квадрата.
3) Найдем радиус описанной окружности, разделив диагональ квадрата пополам.
1) Найдем сторону квадрата:
2) Найдем диагональ квадрата используя теорему Пифагора:
3) Найдем радиус описанной окружности, разделив диагональ квадрата пополам.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Радиус вписанной окружности в квадрат
a – сторона квадрата
Формула радиуса вписанной окружности в квадрат (r):
- Подробности
-
Автор: Administrator
-
Опубликовано: 09 сентября 2011
-
Обновлено: 27 мая 2017
Квадрат представляет собой полностью симметричную фигуру, центр которой является и точкой пересечения всех биссектрис, медиатрис и осей симметрии, а также центром вписанной и описанной окружностей. Радиусы вписанной в квадрат окружности находятся под прямым углом к сторонам квадрата, и каждые два радиуса равны по значению стороне. Поэтому для того чтобы найти радиус окружности, вписанной в квадрат, необходимо разделить сторону на два или разделить диагональ на два корня из двух:
Окружность вписанная в квадрат
Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. 
У квадрата:
- все углы прямые, то есть, равны 90°;
- все стороны, как и углы, равны;
- диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.
При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.
Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:
Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.
Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:
Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата: 
Находим из этого уравнения неизвестное значение: 
.
Окружность описанная около квадрата
Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):
Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:
- угол CDA=90°;
- стороны AD=CD. Признак равнобедренного треугольника;
- угол DAC равен ACD. Они равны по 45°.
Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:
, отсюда 
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:
Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:
Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна 
, тогда:
Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.
Рассмотрим пример
Задача
: радиус окружности вписанной в квадрат равен 
. Найти радиус окружности описанной около этого квадрата.
Дано
:
- треугольник ОСЕ – равнобедренный и прямоугольный;
- ОЕ=ЕС=
; - ОЕС=90°;
- ЕОС=ОСЕ=45°;
Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.
