Как найти радиус вращения конуса

1) Если вам известны объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3∙πR²H. Получите: R²=3V/πH, откуда R=√ (3V/πH)

. 2) Если вам известны площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=πRL. Вы получите R=S/πL.

3) Следующие способы нахождения радиуса основания конуса базируются на утверждении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам известны высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L²=R²+H². Выразите из данной формулы R, получите: R²=L²-H² и R=√ (L²-H²).

4) Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если известны образующая конуса L и угол α между высотой конуса и его образующей, найдите радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L∙sinα.

5) Если известны образующая конуса L и угол β между радиусом основания конуса и его образующей, найдите радиус основания R по формуле: R=L∙cosβ. Если известны высота конуса H и угол α между его образующей и радиусом основания, найдите радиус основания R по формуле: R=H∙tgα.

6) Пример: образующая конуса L равна 20 см и угол α между образующей и высотой конуса равен 15º. Найдите радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом α противолежащий этому углу катет R вычисляется по формуле R=L∙sinα. Подставьте соответствующие значения, получите: R=L∙sinα=20∙sin15º. Sin15º находится из формул тригонометрических функций половинного аргумента и равен 0,5√ (2-√3). Отсюда катет R=20∙0,5√ (2-√3) = 10√ (2-√3) см. Соответственно, радиус основания конуса R равен 10√ (2-√3) см.

7) Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30º, равен половине гипотенузы. Таким образом, если известны длина образующей конуса и угол между его образующей и высотой равен 30º, то найдите радиус по формуле: R=1/2L.

Радиус и образующая конуса

Свойства

Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π. d=2r P=2πr S_(осн.)=πr^2

Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2) h=√(l^2-r^2 ) cos⁡β=r/l α=180°-2β

Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса. S_(б.п.)=πrl S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)

Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту. V=1/3 S_(осн.) h=(πr^2 h)/3

Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4) r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r) R=l^2/2h

Нахождение радиуса/площади/объема описанной около конуса сферы (шара)

В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.

Нахождение радиуса сферы/шара

Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.

Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.

Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие ( l ) – его боковые стороны (AB и BC).

Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:

1. Через образующую и радиус основания конуса:

2. Через высоту и радиус основания конуса

Высота (h) конуса – это отрезок BE на рисунках выше.

Формулы площади и объема сферы/шара

Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:

Примечание: π округленно равняется 3,14.

Найти радиус окружности конуса

Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .

Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.

Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).

Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).

Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a ), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б ), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в ), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г ), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д ). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.

 ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.

Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.

Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .

Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = АВ • РC. Имеем: ОР = R (по условию); в △ A OB : ОС = ; в △ ОСР : CP = = .

Тогда S △ ABP = АВ • РС = .

Ответ: а) .

18.3. Касательная плоскость к конусу

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.

18.4. Изображение конуса

Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).

Для достижения наглядности изображения невидимые линии изображают штрихами.

Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.

18.5. Развёртка и площадь поверхности конуса

Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .

Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):

α = .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.

Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле

S бок = α • l 2 , (1)

где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:

Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼

Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.

S кон = π Rl + π R 2 . (3)

Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому

S бок = 2 π ВС • AD. (4)

Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем

= ⇒ BC • AD = DE • АС. (5)

Тогда соотношение (4) принимает вид

S бок = (2 π • DE ) • AC, (6)

т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.

Это следствие будет использовано в п. 19.7.

18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).

Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .

Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F 1 , при этом центр О основания отображается на центр О 1 круга F 1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X 1 = РX ∩ α . Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

= = k, (*)

где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.

А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.

Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

S сечен : S основ = k 2 = : PO 2 .

18.7. Вписанные в конус и описанные около конуса пирамиды

Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.

Для построения изображения правильной пирамиды, вписанной в конус:

— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;

— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;

— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.

На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:

— прямоугольный треугольник (см. рис. 179);

[spoiler title=”источники:”]

http://reader.lecta.rosuchebnik.ru/demo/8285/data/chapter19.xhtml

[/spoiler]

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание! Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

• Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

• Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

• Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.

Основные сведения

• R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB.
• h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD.
• Точка C – вершина конуса.
• l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания.
• Осевое сечение конуса – это равнобедренный треугольник ABC, который образуется в результате пересечения конуса плоскостью проходящей через его ось.
• Поверхность конуса – состоит из его боковой поверхности и основания. Формулы для расчета площади поверхности, а также объема прямого кругового конуса представлены в отдельных публикациях.

Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):

l2 = h2 + R2

Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.

• длина дуги сектора равняется длине окружности основания конуса (т.е. 2πR);
• α – угол развёртки (или центральный угол);
• l – радиус сектора.

Виды конусов

1. Прямой конус – имеет симметричное основание. Ортогональная проекция вершины данной фигуры на плоскость основания совпадает с центром этого основания.
2. Косой (наклонный) конус – ортогональная проекция вершины фигуры на ее основание не совпадает с центром этого основания.
3. Усеченный конус (конический слой) – часть конуса, которая остается между его основанием и секущей плоскостью, параллельной данному основанию.
4. Круговой конус – основанием фигуры является круг. Также бывают: эллиптический, параболический и гиперболический конусы.
5. Равносторонний конус – прямой конус, образующая которого равняется диаметру его основания.

Свойства кругового конуса

Выделяют несколько особенностей, которыми обладает фигура данного типа:

1. Образующие кругового конуса равны друг другу.
2. Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.
3. Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.

Интересный факт! Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.

Общая формула объёма фигуры

Чтобы найти объём кругового конуса, необходимо умножить число Пи на его высоту, на радиус в квадрате и всё это произведение поделить на три:

Дополнительная информация! Чтобы узнать объём фигуры, нужно умножить площадь её основы на высоту и поделить на три:

Расчет объема

Формула объема любого конуса выглядит следующим образом:

V = 1/3 * π * h * r2

где

• V – это объем конуса;
• h – высота;
• r – радиус;
• π — константа, равная 3,14.

Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.

Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a2+ b2= c2 или в нашем случае h2+ r2= l2, где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:

a = √c2- b2

То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:

h = √l2 — r2

Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.

Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:

r = √l2 — h2

После чего по той же формуле, что указана выше, рассчитать объем конуса.

Объём усечённого конуса

Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:

Объём данного тела можно вычислить по формуле:

Важно! S и S1 это площади соответствующих основ, которые равняются ПR2 и ПR12 При нахождении этих значений поможет онлайн калькулятор.

Первый способ вычисления объема усеченного конуса

Объем усеченного конуса вычисляется по формуле:

[ LARGE V = frac{1}{3} left( Hcdot S_2 + h cdot s_1 right) ]

где:

• V – объем конуса
• h – расстояния от плоскости верхнего основания до вершины
• H – расстояния от плоскости нижнего основания до вершины
• S1 – площадь верхнего (ближнего к вершине) основания
• S2 – площадь нижнего основания

Второй способ вычисления объема усеченного конуса

Объем усеченного конуса вычисляется по формуле:

[ LARGE V = frac{1}{3} pi h left( R^2 + R cdot r + r^2 right) ]

где:

• V – объем конуса
• h – высота конуса
• R – радиус нижнего основания
• r – радиус верхнего основания

Объем наклонного конуса

Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.

Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.

Площадь поверхности фигуры

Для вычисления данного параметра потребуется знать площадь боковой поверхности. Она равняется произведению числа π, радиуса и длины образующей.

Чтобы рассчитать площадь всей поверхности, нужно сложить площади его основы и боковой поверхности.

Формула образующей конуса

Образующую конуса можно найти, зная ее высоту H и радиус R:

L = √H2 + R2

Формула площади боковой поверхности конуса

Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:

Sбок.пов = πRL

Формула площади основания конуса

Площадь основания конуса можно вычислить по его радиусу R:

Sосн = πR2

Сечение конуса

Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.

Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.

Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.

Площадь сечения

Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:

S = 1/2 * d * h или S = 1/2 * 2r * h

где

• S – это площадь сечения;
• d – диаметр основания;
• r – радиус;
• h – высота.

В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.

Площадь усечённого конуса

Для нахождения данного параметра нужно воспользоваться формулами:

• площади боковой поверхности усечённого конуса Sбок;
• полной площади усечённой фигуры Sпол, которая равна сумме площадей двух оснований и площади боковой поверхности:

Здесь l — длина образующей, а R и r — радиусы большего и меньшего оснований соответственно.

Уравнение конуса

Часто требуется при решении математических задач. Записывается в следующем виде:

где x0, y0,z0- координаты по соответствующим осям.

Таким образом, в данной статье были представлены основные сведения, которые могут понадобиться при решении задач на тему «Конус».

Составляющие конуса

Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.

Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.

Конус состоит из следующих элементов:

1. Круга, являющегося его основанием.
2. Боковой поверхности.
3. Точки, не лежащей в плоскости основания, называющейся вершиной конуса.
4. Отрезков, которые соединяют точки круга основания геометрического тела и его вершину.

Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.

Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.

Длина образующих в прямом конусе

Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.

То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:

l2 = r2+ h2 или l = √r2 + h2

где

• l – образующая;
• r – радиус;
• h – высота.

Образующая в наклонном конусе

Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.

Прежде всего необходимо знать высоту, длину оси и радиус основания.

Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:

r1= √k2 — h2

где

• r1 – это часть радиуса между осью и высотой;
• k – длина оси;
• h – высота.

В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:

R = r + r1

где

• R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
• r – радиус основания;
• r1 – часть радиуса между осью и высотой.

Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:

l = √h2+ R2

или, не производя отдельно расчет R, объединить две формулы в одну:

l = √h2 + (r + r1)2.

Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу — использованию теоремы Пифагора.

Примеры задач

Задание 1
Найдите объем конуса, если известна площадь его основания – 50,24 см2, а также, высота – 9 см.

Решение:
Применим первую формулу, подставив в нее заданные значения:

Задание 2
Высота конуса равна 7 см, а его радиус – 4 см. Найдите объем фигуры.

Решение:
Воспользовавшись второй, более расширенной, формулой получаем:

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 ноября 2022 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Конус (значения).

Ко́нус (через нем. Konus и лат. cōnus, от др.-греч. κώνος^[1] — «сосновая шишка»^[2]) — поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса)^[3].

Если направляющая конуса — замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют «конусом» (см. рисунок), а внутренность этой кривой называют «основанием конуса», если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Иногда вместо лучей рассматривают прямые, тогда получается двойной конус, состоящий из двух симметричных относительно вершины частей.

Конус и связанные с ним конические сечения играют большую роль в математике, астрономии и других науках.

Связанные определения[править | править код]

• Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
• Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
• Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
• Конусность — соотношение высоты и диаметра основания конуса.

Типы конусов[править | править код]

• 

  Прямой круговой конус

• 

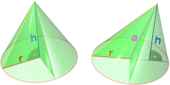
  Прямой и косой круговые конусы с равным основанием и высотой: их объём одинаков

• 

  Усечённый прямой круговой конус

• Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
• Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
• Круговой конус — конус, основание которого является кругом.
• Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
• Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
• Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
• Равносторонний конус — конус вращения, образующая которого равна диаметру основания ^[4].

Свойства[править | править код]

• Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
• Телесный угол при вершине прямого кругового конуса равен

где α — угол раствора конуса.

• Площадь боковой поверхности прямого кругового конуса равна

а в общем случае

где R — радиус основания, — длина образующей, — длина границы основания.

Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна

для прямого кругового конуса и

для произвольного, где — площадь основания.

• Объём кругового (не обязательно прямого) конуса равен

• Для усечённого кругового конуса (не обязательно прямого) объём равен:

где и  — радиусы соответственно нижнего и верхнего оснований, — высота от плоскости нижнего основания,до верхнего основания.

• Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:

где и  — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, и  — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

• Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

Уравнение прямого кругового конуса[править | править код]

Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:

• В сферической системе координат с координатами (r, φ, θ):

• В цилиндрической системе координат с координатами (r, φ, z):

или

• В декартовой системе координат с координатами (x, y, z):

Это уравнение в каноническом виде записывается как

где константы a, с определяются пропорцией Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид

причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением где функция  является однородной, то есть удовлетворяющей условию для любого действительного числа α.

Развёртка[править | править код]

Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора в развёртке боковой поверхности конуса определяется по формуле:

φ = 360°·(r/l).

Вариации и обобщения[править | править код]

См. также[править | править код]

• Коническая поверхность
• Коническое сечение
• Конус (топология)
• Световой конус

Примечания[править | править код]

Литература[править | править код]

• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — 720 с.
• Конус // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 288. — 847 с.

В данной статье рассмотрим четыре задачи по стереометрии. Дана комбинация тел – конус и шар. Во всех заданиях речь идёт о конусе, который . Отмечу, что в условии взаимное расположение данных тел озвучено может быть по разному, например: «Конус вписан в шар» или «Около конуса описана сфера».

Суть одна – если сказать простым (нематематическим) языком, то конус находится «внутри» сферы, она содержит окружность его основания и вершину. Посмотрите на эскиз:

При решении необходимо знать формулы объёмов шара и конуса.

Объём шара:

Объём конуса:

*Эти формулы необходимо знать!

Площадь основания конуса является кругом, она равна:

Рассмотрим частный случай! Если высота конуса будет равна радиусу его основания, то формула объёма конуса будет иметь вид:

Эскиз:

Понятно, что центральным сечением такого конуса будет являться прямоугольный равнобедренный треугольник, причём высота проведённая из прямого угла разбивает его также на два прямоугольных равнобедренных треугольника:

Вспомним понятие образующей, оно часто используется в задачах с конусами, будет и в заданиях ниже.

Образующая конуса – это отрезок, соединяющий вершину конуса с точкой его основания. На предыдущем эскизе она обозначена буквой l .

Напрашивается простой вывод: образующих у конуса имеется бесконечное количество и все они равны.

На блоге, кстати, уже есть пара статей с шарами, можете посмотреть их « » и « » .

Теперь рассмотрим задачи:

245351. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

Так как сказано, что радиус основания конуса равен радиусу шара, то становится понятно, что основание конуса совпадает с плоскостью центрального сечения шара.

Построим эскиз данной комбинации для наглядности (это осевое сечение):

Сказано, что высота конуса равна радиусу его основания (и, разумеется, радиусу шара). Запишем формулы объёмов шара и конуса:

Так как объём шара известен (он равен 28), можем вычислить радиус. Вернее, нам понадобится не сам радиус, а его куб:

Таким образом, объём конуса будет равен:

*Можно было обойтись без вычислений. Посмотрите, если сопоставить две формулы:

то видно, что объём шара в 4 раза больше объёма конуса.

Значит объём конуса будет равен 28/4 = 7.

То есть, задача решается практически устно.

Ответ: 7

245352. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.

Задача обратная предыдущей, рисунок тот же.

Формулы:

Из формул понятно, что объём шара в 4 раза больше объёма конуса:

Таким образом, искомый объём равен 24.

Ответ: 24

316555. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна . Найдите радиус сферы.

Здесь условие звучит по-другому, но тела расположены относительно друг друга абсолютно также, как и в предыдущих задачах – конус вписан в сферу, основание конуса совпадает с центральным сечением сферы.

Эскиз тот же, отметим радиус, высоту равную радиусу и образующую:

«Конус геометрия» – Вершина. Конус. Образующие. Основание. С конусом люди знакомы с глубокой древности. H-высота. Применение конуса и усеченного конуса в повседневной жизни. R-радиус основания. Центр основания. Конус в переводе с греческого «konos» означает «сосновая шишка». L-образующая.

«Атмосферное давление и высота» – Слон использует атмосферное давление всякий раз, когда хочет пить. 5. Ливер – предназначен для взятия проб различных жидкостей. Изучение новой темы. Организационный момент: приветствие, постановка цели и мотивация урока. Опускаем шприц в жидкое лекарственное средство. То же самое наблюдается и в природе – в водоеме.

«Конус 11 класс» – Площадь полной поверхности конуса. Площадь боковой поверхности усечённого конуса. Конус. Площадь боковой поверхности конуса. V = 1/3sосн.h. Объём усечённого конуса. Sбок= п(r+r1)l. Геометрия 11 класс. Объём конуса. Усечённый конус. Конус- тело ограниченное конической поверхностью и кругом с границей L.

«Медиана биссектриса и высота треугольника» – На каком рисунке изображена высота? отрезок, соединяющий вершину треугольника с серединой противолежащей стороны Биссектриса треугольника Медиана треугольника Высота треугольника. Медиана, биссектриса и высота треугольника. отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны Медиана треугольника Высота треугольника Биссектриса треугольника.

«Цилиндр конус шар» – Сечения цилиндра. Объёмы и поверхности тел вращения. Найти объём и площадь поверхности шара. Определение цилиндра. Оглавление. Объёмы тел вращения. Тела вращения. Объём шарового сегмента. Задача № 3. Площади поверхностей тел вращения. Определение шара. Виды тел вращения. Сечение конуса. – Шаровые сегменты.

«Громкость и высота звука» – Что такое звук? Механические колебания каких частот называются звуковыми? Громкость и высота звука. Контрольный тест. Кто в полёте чаще машет крыльями: муха или комар? Назовите физические характеристики звука. Балалайка. Уровень звукового давления, дБ. Назовите причины возникновения звука. Звук. Саксофон.

Прямой конус – это тело, которое получается при вращении прямоугольного треугольника вокруг одного из катетов. Этот катет есть высота конуса H, другой катет является радиусом его основания R, гипотенуза равна множеству образующих конуса L. Способ нахождения радиуса конуса зависит от исходных данных задачи.

Спонсор размещения P&G Статьи по теме “Как найти радиус основания конуса” Как найти площадь конуса Как найти площадь треугольника Как найти площадь прямоугольной призмы Как найти площадь грани в пирамиде Как найти перпендикуляр в треугольнике

Инструкция

Если вам известны объем V и высота конуса H, выразите его радиус основания R из формулы V=1/3 ?R?H. Получите: R?=3V/?H, откуда R=v(3V/?H). Если вам известны площадь боковой поверхности конуса S и длина его образующей L, выразите радиус R из формулы: S=?RL. Вы получите R=S/?L.

Следующие способы нахождения радиуса основания конуса базируются на утверждении, что конус образован при вращении прямоугольного треугольника вокруг одного из катетов к оси. Так, если вам известны высота конуса H и длина его образующей L, то для нахождения радиуса R вы можете воспользоваться теоремой Пифагора: L?=R?+H?. Выразите из данной формулы R, получите: R?=L?–H? и R=v(L?–H?). Используйте правила соотношений между сторонами и углами в прямоугольном треугольнике. Если известны образующая конуса L и угол? между высотой конуса и его образующей, найдите радиус основания R, равный одному из катетов прямоугольного треугольника, по формуле: R=L sin?. Если известны образующая конуса L и угол? между радиусом основания конуса и его образующей, найдите радиус основания R по формуле: R=L cos?. Если известны высота конуса H и угол? между его образующей и радиусом основания, найдите радиус основания R по формуле: R=H tg?.

Пример: образующая конуса L равна 20 см и угол? между образующей и высотой конуса равен 15?. Найдите радиус основания конуса. Решение: В прямоугольном треугольнике с гипотенузой L и острым углом? противолежащий этому углу катет R вычисляется по формуле R=L sin?. Подставьте соответствующие значения, получите: R=L sin?=20 sin15?. Sin15? находится из формул тригонометрических функций половинного аргумента и равен 0,5v(2–v3). Отсюда катет R=20 0,5v(2–v3)=10v(2–v3)см. Соответственно, радиус основания конуса R равен 10v(2–v3)см. Частный случай: в прямоугольном треугольнике катет, противолежащий углу в 30?, равен половине гипотенузы. Таким образом, если известны длина образующей конуса и угол между его образующей и высотой равен 30?, то найдите радиус по формуле: R=1/2L. Как просто

Другие новости по теме:

Если вблизи вершины конуса провести сечение, можно получить идентичную, но иную по форме и размерам фигуру, называемую усеченным конусом. Она имеет не один, а два радиуса, один из которых меньше другого. Как и у обычного конуса, у этой фигуры имеется высота. Спонсор размещения P&G Статьи по теме

Усеченным конусом называется геометрическое тело, которое получилось в результате сечения полного конуса плоскостью, параллельной его основанию. Согласно другому определению, усеченный конус образован вращением прямоугольной трапеции вокруг той ее боковой стороны, которая перпендикулярна

Тем, кто занимается моделированием и бумажной пластикой, необходимо уметь делать развертки разнообразных геометрических тел. В школьной геометрии конус определяют как геометрическое тело, которое получается в результате объединения всех лучей, исходящих из одной точки, называемой вершиной конуса,

Площадью основания конуса является круг. Для нахождения его площади надо знать радиус окружности, содержащей этот круг, либо какие-нибудь другие данные, расчеты которых математически связаны с площадью основания конуса. Спонсор размещения P&G Статьи по теме “Как найти площадь основания конуса” Как

Конус представляет собой геометрическое тело, основание которого представляет собой круг, а боковая поверхности – все отрезки, проведенные из точки, находящейся вне плоскости основания, к этому основанию. Прямой конус, который обычно рассматривается в школьном курсе геометрии, можно представить как

Конус – это тело, в основании которого лежит круг. Вне плоскости этого круга находится точка, называемая вершиной конуса, а отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Вам понадобится Бумага, карандаш, калькулятор Спонсор размещения P&G