Как найти радиус земли по длине экватора

Как найти радиус Земли зная длину экватора: подробный гайд

Размеры нашей планеты были измерены людьми с тысячелетней историей назад. С тех пор наука и технологии продвинулись настолько, что мы можем точно определить радиус Земли, используя современные методы измерения и математические формулы. В этой статье мы поговорим о том, как найти радиус Земли, используя длину экватора и другие факторы.

Определение радиуса Земли

Радиус Земли — это расстояние от центра Земли до ее поверхности. Радиус Земли не является постоянным и колеблется от местности к местности. Существует несколько способов определения радиуса Земли:

• Метод гравиметрических измерений
• Метод лазерного измерения расстояний от Земли до Луны
• Метод астрономических измерений
• Метод геодезических измерений

В этой статье мы расскажем о методе геодезических измерений, который позволит вам вычислить радиус Земли, если у вас есть длина экватора.

Метод геодезических измерений

Метод геодезических измерений основан на использовании геодезических инструментов, таких как теодолиты, нивелиры и другие приборы, для измерения угловых и линейных расстояний на Земле.

С помощью геодезических инструментов можно определить расстояния между двумя точками на земной поверхности и угол между линией, соединяющей эти точки, и экватором Земли.

Отметим, что для определения радиуса Земли с помощью метода геодезических измерений требуется несколько известных параметров:

• Длина экватора Земли (в километрах)
• Широта точки
• Высота над уровнем моря точки

Формула для вычисления радиуса Земли

Для вычисления радиуса Земли с помощью метода геодезических измерений применяется формула:

r = L / 2π

где:

• r — радиус Земли
• L — длина экватора Земли
• π — число «Пи», равное приблизительно 3,14159

Таким образом, для вычисления радиуса Земли необходимо разделить длину экватора на 2π.

Пример нахождения радиуса Земли

Допустим, длина экватора Земли равна 40,075 км. Чтобы вычислить радиус Земли, нужно поделить 40,075 на 2π:

r = 40075 / 2π ≈ 6 371,01 км

Итак, радиус Земли составляет примерно 6 371,01 км.

Вывод

Как можно увидеть, определение радиуса Земли может быть достаточно простым, если известна длина ее экватора. Для этого применяется метод геодезических измерений и математическая формула, основанная на числе «Пи». Полученный результат может незначительно изменяться в зависимости от местности и других факторов. Теперь, когда вы знаете, как найти радиус Земли по длине экватора, вы сможете проявить себя в науке и сделать свой вклад в изучение нашей планеты.

Как найти радиус земли зная длину экватора

Радиус Земли — это расстояние от центра Земли до ее поверхности. Знание радиуса Земли является важной информацией в различных областях науки, таких как геология, астрономия и геодезия. Существует множество способов вычисления радиуса Земли, и в этой статье мы обсудим, как найти радиус Земли, зная длину экватора.

Что такое экватор?

Экватор — это географическая линия, которая делит Землю на две части — северную и южную половины, и находится на расстоянии 0° широты. Длина экватора составляет около 40 075 км.

Расчет радиуса Земли

Существует несколько способов вычисления радиуса Земли, но один из самых простых — это использование длины экватора и формулы:

(1) C = 2πr

где C — длина экватора, r — радиус Земли, π — математическая константа, примерно равная 3,14.

Мы можем переписать (1) следующим образом:

(2) r = C / 2π

Подставляя значение C = 40 075 км и π = 3,14 в (2), мы получаем:

r ≈ 6 378 км.

Таким образом, радиус Земли составляет примерно 6 378 км.

Точность расчета

Обратите внимание, что значение радиуса Земли, полученное с помощью формулы (2), является приблизительным, поскольку мы использовали приблизительное значение для π и не учитывали, что Земля не является идеальной сферой. Более точный способ вычисления радиуса Земли — это использование исходных данных, полученных при различных углах наблюдения, и математических моделей на основе этих данных. Однако, для многих практических целей, приближенное значение радиуса Земли, полученное с помощью формулы (2), является достаточно точным и используется повсеместно.

Вывод

В данной статье мы обсудили, как найти радиус Земли, зная длину экватора. Радиус Земли — важная характеристика нашей планеты, и его знание является необходимым в различных областях науки и инженерии. Формула (2) позволяет легко вычислить приближенное значение радиуса Земли, используя только известное значение длины экватора и математическую константу π. Несмотря на то, что это приближение, оно является достаточно точным для большинства практических задач.

Как найти радиус Земли, зная длину экватора

Земля — это огромная планета, которая населяется миллионами видов живых существ. Но что нам известно об этой планете? В наше время, мы обладаем огромным количеством информации об этой планете благодаря научному прогрессу. Сегодня мы рассмотрим, как найти радиус Земли, зная длину экватора.

Понимание терминов

Прежде чем мы перейдём к методам нахождения радиуса Земли, необходимо понимать несколько терминов. Экватор — это линия достаточной меридиональности, которая делит Землю на две части — северную и южную, проходя через ее центр. Радиус Земли — это расстояние от ее центра до ее поверхности.

Методы нахождения радиуса Земли

• Использование формулы

  Существует формула для расчета радиуса Земли, используя ее длину экватора. Эта формула известна как формула Эратосфена. Она основана на предположении, что Земля является идеальным шаром с радиусом R. Этот метод также позволяет найти длину экватора. Формула выглядит следующим образом:

  

  R = L/2π

  где L — длина экватора.

  Подставляя значение L в формулу, мы получаем:

  R = 40,075 км/2π ≈ 6,371 км

  Значение радиуса Земли составляет примерно 6,371 км.

• С помощью спутников

  Современные спутники позволяют точно измерять радиус Земли. Этот метод основан на измерении времени, которое требуется для того, чтобы связь между спутником и приемником проходила через различные позиции на поверхности Земли. Измерения производятся с точностью до нескольких миллиметров, и этот метод является наиболее точным из всех.

• Методы геодезии

  

  Методы геодезии также используются для измерения радиуса Земли. Они основаны на измерении силы тяжести на различных точках поверхности Земли и строительство математических моделей, которые позволяют определить радиус Земли.

Вывод

Несмотря на то, что радиус Земли может быть найден несколькими способами, однако, формула Эратосфена — это наиболее удобный и простой способ для расчета. Измерения с помощью спутников и методы геодезии дают более точные результаты, но их использование требует специальных навыков и оборудования. Зная радиус Земли, мы можем вычислить другие характеристики планеты, которые имеют фундаментальное значение для ее изучения.

Диаметр Земли имеет для ученых важное значение. С его помощью можно вычислить площадь нашей планеты и расстояние до ее центра, также он помогает составлять карты и проводить запуски космических летательных аппаратов. Узнаем, как вычисляются эти параметры и каковы их значения.

Основные параметры Земли

1. Диаметр по экватору – 12756 км, по полюсам – 12713 км.
2. Средний радиус – 6371 км. На таком расстоянии от поверхности находится центр ядра. Экваториальный радиус Земли – 6378 км. Расстояние к центру Земли на полюсах – 6356,5 км.
3. Окружность Земли по экватору – 40075 км, а по полюсам – 40008 км.
4. Удаление от Солнца в километрах – приблизительно 150 миллионов. Оно наиболее подходяще для формирования и поддержания жизни. Если бы орбита Земли была ближе или дальше всего на несколько миллионов километров, условия для эволюции жизни были бы намного хуже.
5. Время, за которое Земля совершает один оборот вокруг Солнца – 365 дней 5 часов 48 минут и 46 секунд. В течение 23 часов 46 минут и 4 секунды она совершает оборот вокруг своей оси. Каждые 100 лет эта скорость уменьшается на 0,017 секунд. 140 млн. лет потребуется для того, чтобы длительность суток увеличилась на час.
6. Ось вращения планеты наклонена к плоскости орбиты под углом немногим больше 23 градусов. Это обусловливает сезонность климатических условий и четкую смену времен года. Если бы ось вращения была наклонена на несколько градусов меньше или больше – на Земле создались бы менее благоприятные климатические условия, на больше части поверхности образовались бы ледники.
7. Средняя температура на Земле – примерно 15 °C.
8. Вода занимает примерно 71% всей площади. Ее масса – 1460 миллионов миллиардов тонн. Атмосфера весит в 275 раз меньше. Ее масса – немногим больше 5 квадриллионов тонн.
9. В атмосфере 21 % кислорода. Основную массу занимает азот – биологически инертный газ, его в составе атмосферы 78%.
10. Масса Земли – примерно 6*10²⁴ килограмма.
11. Объем планеты – 1,08*10¹² км³.
12. Площадь земного шара – 510 млн км².
13. Плотность – 5,5 г/см³.
14. Наиболее близкое к нам небесное тело – Луна. Ее среднее расстояние от Земли – примерно 384 тыс. км.

Форма планеты

На вопрос, какая форма у Земли, большинство людей ответит, что шарообразная. И здесь они сделают ошибку. На планету влияют силы гравитации: огромная масса тяготеет к ядру, поэтому происходит постоянное сжатие. Наиболее сильная центробежная сила, появляющаяся из-за движения Земли вокруг собственной оси – на экваторе.

Земля является своего рода «неправильным шаром». Сжатие является причиной того, что экваториальный диаметр планеты немногим больше, чем по полюсам. Ученые определяют форму нашей планеты как близкую к «сплюснутому эллипсоиду».

Интересно, что по причине пренебрежения сжатием Земли по полюсам, эталон метра от 1795 года оказался на 200 микрон короче.

В форме планеты важна также местная топография. Конечно же, она не может в глобальном масштабе влиять на форму планеты. Так, различия между горой Эверест и Марианской впадиной составляет примерно 19 км. В глобальных масштабах эта цифра незначительна. Максимальное расстояние от центра Земли до экватора, учитывая выпуклость земной поверхности  – это вершина вулкана Чимборасо, находящегося в Эквадоре.

Что такое экватор и для чего он нужен

Под экватором следует понимать линию, перпендикулярную оси, вдоль поверхности Земли, на одинаковом расстоянии от полюсов.

Вдоль всей этой линии день равняется ночи. Правда, из-за атмосферной рефракции продолжительность дня больше на несколько минут. Два раза в год (в дни равноденствий) Солнце находится в зените, и лучи будут направляться строго перпендикулярно земной поверхности. Широта на экваторе – 0°.

Экватор имеет важнейшее значение для определения широты географического объекта.  Все точки, находящиеся к югу от воображаемой линии, имеют южную широту. А объекты, располагающиеся к северу от нее, соответственно, имеют северную широту.

Как измерить длину окружности земли

Размер Земли поддается вычислению. Для измерения длины окружности Земли пользуются высокотехнологичными приборами и спутниками. Однако до появления этих изобретений приходилось пользоваться математическими методами измерений. В 18 веке ученые П. Мешен, А.М. Лежандр, Ц. Кассини использовали способ триангуляции.

Предположим, что нужно измерить дистанцию между некоторыми точками, удаленными на несколько сотен километров. Для этого нам надо построить на местности опорную сеть. Это можно сделать с помощью треугольников. Их вершинами будут места, находящиеся на высоте. На них сооружаются воображаемые пирамиды так, чтобы они направлялись на близко расположенные пункты.

Воображаемые фигуры должны быть удобными для установки угломера и вычисления градусов углов. В одном из треугольников измеряют одну сторону, пролегающую по ровной местности. Это будет базис.

Простейший способ измерения длины экватора – умножить количество километров в одном градусе на 360.

Измерение окружности начинается с треугольника, являющегося базисом. По стороне и по углам вычисляется другие стороны этой фигуры. Одна из них является также стороной смежного треугольника. Она же является исходной для определения сторон иного треугольника. В ходе математических вычислений можно найти параметры последнего треугольника. Так можно получить значение дуги меридиана. Чем длиннее дуги меридианов, тем лучше можно вычислить нужную величину – радиус нашей планеты.

Когда известна протяженность дуги меридиана, несложно посчитать, какая будет длина одного градуса. Такой метод является основой геодезии.

Как вычислить радиус и диаметр планеты

Радиус и диаметр Земли вычислить несложно. Для этого пользуются формулами d=l/π; r=½*π. Буквы означают:

• d – диаметр;
• l – протяженность окружности;
• r – радиус (линия, проложенная от центра и до любой точки на окружности);
• π – число, приблизительно равное 3,14.

Измерение окружности Земли в древние времена

О длине этой величины было известно еще в Древней Греции. Необходимые расчеты были сделаны древнегреческим математиком, астрономом, географом Эратосфеном. Ему было известно о том, что в день солнцестояния 21 июня в Сиене, находящейся за полтысячи миль от Александрии, в полдень освещалось дно колодцев, а от предметов не обнаруживалась тень. Выходит, Солнце в этом участке планеты было в зените. В Александрии ничего подобного не происходило.

В полдень летнего солнцестояния ученый измерил тень от городского обелиска (ему была известна его высота). Так было установлено, что Александрию и Сиену отделяет 7 градусов широты.

Астроном делал вычисления дальше. 7° – это примерно одна пятидесятая часть окружности, равняющейся 360°. Умножив расстояние от Сиены до Александрии на 50, у математика получилось число 25000. Стольким милям равнялась окружность Земли.

Длина окружности Земли, рассчитанная Эратосфеном, немного меньше фактической. Это объясняется не примитивностью расчетов: этот способ узнать окружность Земли достаточно точный. Во времена жизни Эратосфена никто не знал точной дистанции между этими населенными пунктами. Также ученый не принял во внимание то, что оба города расположены на двух разных меридианах.

В средние века упоминания о подобных исследованиях были запрещены церковью. Только в 16 веке кругосветное путешествие Ф. Магеллана позволило убедиться, что планета действительно имеет округлую форму, и что окружность ее действительно равна 40 тыс. км.

Сколько времени нужно, чтобы обойти вокруг Земли пешком

Зная сколько километров составляет длина окружности Земли по экватору, можно вычислить, сколько времени понадобится, чтобы обойти его пешком. Если взять за основу обычную скорость пешехода 6 километров в час, то, воспользовавшись формулой t=S/V, можно получить значение примерно 6700 часов, или 278 суток.

Столько понадобится для того, чтобы пройти пешком вокруг Земли без передышки. Если же допустить, что воображаемый пешеход будет каждый день проходить по 6 часов, то для совершения такого путешествия ему понадобится около 1110 суток, или более 3 лет.

Интересная информация об экваторе Земли

На экваторе круглогодично жаркий и влажный климат. Леса Амазонки и экваториальной Африки, Индонезии отличаются разнообразием растительного и животного мира. Днем температура колеблется между 25 и 30 градусами. Ночью не намного холоднее: настолько сильно прогревается поверхность земли солнечными лучами.

Однако экватор интересен некоторыми географическими особенностями:

• он проходит сквозь более 30 островов;
• пересекает 14 стран;
• Эквадор имеет такое название в честь экватора;
• в большинстве экваториальных государств установлены памятники и памятные знаки в честь нулевой параллели;
• недалеко города Кито располагается вулкан Каямбе высотой около 4,7 км, с белеющей от вечного льда вершиной (и это несмотря на то, что экваториальный климат отличается постоянной жарой);
• река Конго, которая течет в центре африканского материка, проходит через нулевую параллель дважды;
• поскольку в рассматриваемой области Земля обращается очень быстро, здесь легче всего запускать спутники: они быстрее набирают необходимую скорость.

Размеры Земли – одни из главных параметров в астрономии и имеет большое практическое значение. С ее помощью можно узнать диаметр и радиус Земли. Вычислить эти параметры можно, применяя несложные математические вычисления.

Земля представляет собой шар с радиусом 6 371 км, а если умножить это значение на 2, то диаметр составит 12 742 км. Эти значения, однако, рассматривают планету как идеальную сферу, игнорируя вариации рельефа.

Дело в том, что на самом деле земной шар слегка приплюснут у полюсов — похож на апельсин. Это сплющивание едва заметно: разница в диаметрах, измеренных в направлении экватора и с севера на юг, составляет всего 40 км.

Человечество знает об этих измерениях уже более двух тысяч лет, благодаря расчетам, сделанным математиком Эратосфеном, родившимся в Киринее, ныне Ливия. Современные спутники показывают, что ученый ошибся в значении окружности — формула которой в 2π раз больше радиуса — всего на 500 км, что впечатляет, учитывая ограничения того времени.

Чтобы получить представление о размерах планеты, мы можем сравнить расстояние до центра Земли с расстояниями на поверхности. Радиус Земли в 6 371 км эквивалентен.

Каков радиус земли

Радиус Земли различается в зависимости от того, какую ее часть мы измеряем, по этой причине существует три основных радиуса :

• Экваториальный радиус 6 378,1 км
• Радио Полярный 6 356,8 км
• Средний радиус 6 371,0 км

Чтобы понять это немного больше, мы также должны знать, что такое радиус и что он представляет.

А как насчет радиуса других планет?

Земля и так огромна, ее радиус составляет чуть более 6 000 км, но другие измерения в Солнечной системе еще больше. Радиус Урана (25 362 км) в четыре раза больше, а радиус Сатурна в девять раз больше земного (58 232 км). Юпитер, самая большая планета в нашей системе, имеет радиус почти 70 000 км — в 11 раз больше земного.

Однако наша планета опережает по размерам Венеру, Марс и Меркурий. Радиус Венеры всего на 300 км меньше (6 052 км), радиус Марса составляет почти половину (3 390 км) от нашего, а радиус Меркурия — около трети (2 440 км). Радиус карликовой планеты Плутон составляет около 1/5 радиуса Земли.

Как измеряется радиус?

В идеальном круге радиус измеряется очень простым способом. Из центра круга берут линейку и измеряют расстояние до края круга. Это расстояние называется радиусом.

В сфере, трехмерном объекте, таком как мрамор, расчет в основном такой же, берется центр сферы и измеряется одна из сторон.

Поскольку планета Земля не является идеальной сферой, она имеет несколько радиусов разной длины, поэтому у нас есть экваториальный радиус, полярный радиус и средний, так как в зависимости от того, куда мы «повернем» линейку, мы будем иметь разные расстояние.

Какая разница в процентах между экваториальным радиусом Земли и полярным радиусом?

Теоретическое предсказание Ньютона предполагало такую разницу в 26 км. Современные измерения показывают, что разница между экваториальным радиусом и полярным радиусом составляет 21,4 км. Такая разница составляет лишь одну часть в 300 от экваториального радиуса Земли (или полярного радиуса).

Как рассчитать кривизну?

Радиус кривизны в данной точке кривой — это, грубо говоря, радиус окружности, которая лучше всего подходит к кривой в этой точке. Кривизна, обозначаемая κ, — это единица, деленная на радиус кривизны.

Какова кривизна Земли?

На реальной Земле угол β мал (почти равен нулю) при высоте h в несколько метров. Для высоты в тысячу метров (1 км) угол составляет всего один градус.

Earth radius
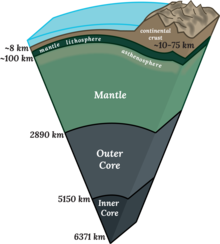
Cross section of Earth’s Interior
General information
Unit system	astronomy, geophysics
Unit of	distance
Symbol	R🜨 or ,
Conversions
1 R🜨 in …	… is equal to …
SI base unit	6.3781×106 m[1]
Metric system	6,357 to 6,378 km
English units	3,950 to 3,963 mi

Earth radius (denoted as R_🜨 or ) is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) (equatorial radius, denoted a) to a minimum of nearly 6,357 km (3,950 mi) (polar radius, denoted b).

A nominal Earth radius is sometimes used as a unit of measurement in astronomy and geophysics, which is recommended by the International Astronomical Union to be the equatorial value.^[1]

A globally-average value is usually considered to be 6,371 kilometres (3,959 mi) with a 0.3% variability (±10 km) for the following reasons.
The International Union of Geodesy and Geophysics (IUGG) provides three reference values: the mean radius (R₁) of three radii measured at two equator points and a pole; the authalic radius, which is the radius of a sphere with the same surface area (R₂); and the volumetric radius, which is the radius of a sphere having the same volume as the ellipsoid (R₃).^[2] All three values are about 6,371 kilometres (3,959 mi).

Other ways to define and measure the Earth radius involve the radius of curvature. A few definitions yield values outside the range between polar radius and equatorial radius because they include local or geoidal topography or because they depend on abstract geometrical considerations.

Introduction[edit]

Earth’s rotation, internal density variations, and external tidal forces cause its shape to deviate systematically from a perfect sphere.^[a] Local topography increases the variance, resulting in a surface of profound complexity. Our descriptions of Earth’s surface must be simpler than reality in order to be tractable. Hence, we create models to approximate characteristics of Earth’s surface, generally relying on the simplest model that suits the need.

Each of the models in common use involve some notion of the geometric radius. Strictly speaking, spheres are the only solids to have radii, but broader uses of the term radius are common in many fields, including those dealing with models of Earth. The following is a partial list of models of Earth’s surface, ordered from exact to more approximate:

• The actual surface of Earth
• The geoid, defined by mean sea level at each point on the real surface^[b]
• A spheroid, also called an ellipsoid of revolution, geocentric to model the entire Earth, or else geodetic for regional work^[c]
• A sphere

In the case of the geoid and ellipsoids, the fixed distance from any point on the model to the specified center is called “a radius of the Earth” or “the radius of the Earth at that point”.^[d] It is also common to refer to any mean radius of a spherical model as “the radius of the earth”. When considering the Earth’s real surface, on the other hand, it is uncommon to refer to a “radius”, since there is generally no practical need. Rather, elevation above or below sea level is useful.

Regardless of the model, any radius falls between the polar minimum of about 6,357 km and the equatorial maximum of about 6,378 km (3,950 to 3,963 mi). Hence, the Earth deviates from a perfect sphere by only a third of a percent, which supports the spherical model in most contexts and justifies the term “radius of the Earth”. While specific values differ, the concepts in this article generalize to any major planet.

Physics of Earth’s deformation[edit]

Rotation of a planet causes it to approximate an oblate ellipsoid/spheroid with a bulge at the equator and flattening at the North and South Poles, so that the equatorial radius a is larger than the polar radius b by approximately aq. The oblateness constant q is given by

where ω is the angular frequency, G is the gravitational constant, and M is the mass of the planet.^[e] For the Earth 1/q ≈ 289, which is close to the measured inverse flattening 1/f ≈ 298.257. Additionally, the bulge at the equator shows slow variations. The bulge had been decreasing, but since 1998 the bulge has increased, possibly due to redistribution of ocean mass via currents.^[4]

The variation in density and crustal thickness causes gravity to vary across the surface and in time, so that the mean sea level differs from the ellipsoid. This difference is the geoid height, positive above or outside the ellipsoid, negative below or inside. The geoid height variation is under 110 m (360 ft) on Earth. The geoid height can change abruptly due to earthquakes (such as the Sumatra-Andaman earthquake) or reduction in ice masses (such as Greenland).^[5]

Not all deformations originate within the Earth. Gravitational attraction from the Moon or Sun can cause the Earth’s surface at a given point to vary by tenths of a meter over a nearly 12-hour period (see Earth tide).

Radius and local conditions[edit]

Given local and transient influences on surface height, the values defined below are based on a “general purpose” model, refined as globally precisely as possible within 5 m (16 ft) of reference ellipsoid height, and to within 100 m (330 ft) of mean sea level (neglecting geoid height).

Additionally, the radius can be estimated from the curvature of the Earth at a point. Like a torus, the curvature at a point will be greatest (tightest) in one direction (north–south on Earth) and smallest (flattest) perpendicularly (east–west). The corresponding radius of curvature depends on the location and direction of measurement from that point. A consequence is that a distance to the true horizon at the equator is slightly shorter in the north–south direction than in the east–west direction.

In summary, local variations in terrain prevent defining a single “precise” radius. One can only adopt an idealized model. Since the estimate by Eratosthenes, many models have been created. Historically, these models were based on regional topography, giving the best reference ellipsoid for the area under survey. As satellite remote sensing and especially the Global Positioning System gained importance, true global models were developed which, while not as accurate for regional work, best approximate the Earth as a whole.

Extrema: equatorial and polar radii[edit]

The following radii are derived from the World Geodetic System 1984 (WGS-84) reference ellipsoid.^[6] It is an idealized surface, and the Earth measurements used to calculate it have an uncertainty of ±2 m in both the equatorial and polar dimensions.^[7] Additional discrepancies caused by topographical variation at specific locations can be significant. When identifying the position of an observable location, the use of more precise values for WGS-84 radii may not yield a corresponding improvement in accuracy.^{[clarification needed]}

The value for the equatorial radius is defined to the nearest 0.1 m in WGS-84. The value for the polar radius in this section has been rounded to the nearest 0.1 m, which is expected to be adequate for most uses. Refer to the WGS-84 ellipsoid if a more precise value for its polar radius is needed.

• The Earth’s equatorial radius a, or semi-major axis, is the distance from its center to the equator and equals 6,378.1370 km (3,963.1906 mi).^[8] The equatorial radius is often used to compare Earth with other planets.

• The Earth’s polar radius b, or semi-minor axis, is the distance from its center to the North and South Poles, and equals 6,356.7523 km (3,949.9028 mi).

Location-dependent radii[edit]

Geocentric radius[edit]

The geocentric radius is the distance from the Earth’s center to a point on the spheroid surface at geodetic latitude φ:

where a and b are, respectively, the equatorial radius and the polar radius.

The extrema geocentric radii on the ellipsoid coincide with the equatorial and polar radii.
They are vertices of the ellipse and also coincide with minimum and maximum radius of curvature.

Radii of curvature[edit]

Principal radii of curvature[edit]

There are two principal radii of curvature: along the meridional and prime-vertical normal sections.

Meridional[edit]

In particular, the Earth’s meridional radius of curvature (in the north–south direction) at φ is:^[9]

where is the eccentricity of the earth. This is the radius that Eratosthenes measured in his arc measurement.

Prime vertical[edit]

If one point had appeared due east of the other, one finds the approximate curvature in the east–west direction.^[f]

This Earth’s prime-vertical radius of curvature, also called the Earth’s transverse radius of curvature, is defined perpendicular (orthogonal) to M at geodetic latitude φ^[g] and is:^[9]

N can also be interpreted geometrically as the normal distance from the ellipsoid surface to the polar axis.^[10]
The radius of a parallel of latitude is given by .^[11][12]

Polar and equatorial radius of curvature[edit]

The Earth’s meridional radius of curvature at the equator equals the meridian’s semi-latus rectum:

b²/a = 6,335.439 km

The Earth’s prime-vertical radius of curvature at the equator equals the equatorial radius, N = a.

The Earth’s polar radius of curvature (either meridional or prime-vertical) is:

a²/b = 6,399.594 km

Derivation[edit]

Combined radii of curvature[edit]

Azimuthal[edit]

The Earth’s azimuthal radius of curvature, along an Earth normal section at an azimuth (measured clockwise from north) α and at latitude φ, is derived from Euler’s curvature formula as follows:^[14]: 97

Non-directional[edit]

It is possible to combine the principal radii of curvature above in a non-directional manner.

The Earth’s Gaussian radius of curvature at latitude φ is:^[14]

Where K is the Gaussian curvature, .

The Earth’s mean radius of curvature at latitude φ is:^[14]: 97

Global radii[edit]

The Earth can be modeled as a sphere in many ways. This section describes the common ways. The various radii derived here use the notation and dimensions noted above for the Earth as derived from the WGS-84 ellipsoid;^[6] namely,

Equatorial radius: a = (6378.1370 km)

Polar radius: b = (6356.7523 km)

A sphere being a gross approximation of the spheroid, which itself is an approximation of the geoid, units are given here in kilometers rather than the millimeter resolution appropriate for geodesy.

Nominal radius[edit]

In astronomy, the International Astronomical Union denotes the nominal equatorial Earth radius as , which is defined to be 6,378.1 km (3,963.2 mi).^[1]: 3 The nominal polar Earth radius is defined as = 6,356.8 km (3,949.9 mi). These values correspond to the zero Earth tide convention. Equatorial radius is conventionally used as the nominal value unless the polar radius is explicitly required.^[1]: 4
The nominal radius serves as a unit of length for astronomy.
(The notation is defined such that it can be easily generalized for other planets; e.g., for the nominal polar Jupiter radius.)

Arithmetic mean radius[edit]

In geophysics, the International Union of Geodesy and Geophysics (IUGG) defines the Earth’s arithmetic mean radius (denoted R₁) to be^[2]

The factor of two accounts for the biaxial symmetry in Earth’s spheroid, a specialization of triaxial ellipsoid.
For Earth, the arithmetic mean radius is 6,371.0088 km (3,958.7613 mi).^[15]

Authalic radius[edit]

Earth’s authalic radius (meaning “equal area”) is the radius of a hypothetical perfect sphere that has the same surface area as the reference ellipsoid. The IUGG denotes the authalic radius as R₂.^[2]
A closed-form solution exists for a spheroid:^[16]

where e² = a² − b²/a² and A is the surface area of the spheroid.

For the Earth, the authalic radius is 6,371.0072 km (3,958.7603 mi).^[15]

The authalic radius also corresponds to the radius of (global) mean curvature, obtained by averaging the Gaussian curvature, , over the surface of the ellipsoid. Using the Gauss–Bonnet theorem, this gives

Volumetric radius[edit]

Another spherical model is defined by the Earth’s volumetric radius, which is the radius of a sphere of volume equal to the ellipsoid. The IUGG denotes the volumetric radius as R₃.^[2]

For Earth, the volumetric radius equals 6,371.0008 km (3,958.7564 mi).^[15]

Rectifying radius[edit]

Another global radius is the Earth’s rectifying radius, giving a sphere with circumference equal to the perimeter of the ellipse described by any polar cross section of the ellipsoid. This requires an elliptic integral to find, given the polar and equatorial radii:

The rectifying radius is equivalent to the meridional mean, which is defined as the average value of M:^[16]

For integration limits of [0,π/2], the integrals for rectifying radius and mean radius evaluate to the same result, which, for Earth, amounts to 6,367.4491 km (3,956.5494 mi).

The meridional mean is well approximated by the semicubic mean of the two axes,^{[citation needed]}

which differs from the exact result by less than 1 μm (4×10⁻⁵ in); the mean of the two axes,

about 6,367.445 km (3,956.547 mi), can also be used.

Topographical radii[edit]

The mathematical expressions above apply over the surface of the ellipsoid.
The cases below considers Earth’s topography, above or below a reference ellipsoid.
As such, they are topographical geocentric distances, R_t, which depends not only on latitude.

Topographical extremes[edit]

• Maximum R_t: the summit of Chimborazo is 6,384.4 km (3,967.1 mi) from the Earth’s center.
• Minimum R_t: the floor of the Arctic Ocean is 6,352.8 km (3,947.4 mi) from the Earth’s center.^[17]

Topographical global mean[edit]

The topographical mean geocentric distance averages elevations everywhere, resulting in a value 230 m larger than the IUGG mean radius, the authalic radius, or the volumetric radius. This topographical average is 6,371.230 km (3,958.899 mi) with uncertainty of 10 m (33 ft).^[18]

Derived quantities: diameter, circumference, arc-length, area, volume [edit]

Earth’s diameter is simply twice Earth’s radius; for example, equatorial diameter (2a) and polar diameter (2b). For the WGS84 ellipsoid, that’s respectively:

• 2a = 12,756.2740 km (7,926.3812 mi),
• 2b = 12,713.5046 km (7,899.8055 mi).

Earth’s circumference equals the perimeter length. The equatorial circumference is simply the circle perimeter: C_e=2πa, in terms of the equatorial radius, a. The polar circumference equals C_p=4m_p, four times the quarter meridian m_p=aE(e), where the polar radius b enters via the eccentricity, e=(1−b²/a²)^0.5; see Ellipse#Circumference for details.

Arc length of more general surface curves, such as meridian arcs and geodesics, can also be derived from Earth’s equatorial and polar radii.

Likewise for surface area, either based on a map projection or a geodesic polygon.

Earth’s volume, or that of the reference ellipsoid, is V = 4/3πa²b. Using the parameters from WGS84 ellipsoid of revolution, a = 6,378.137 km and b = 6356.7523142 km, V = 1.08321×10¹² km³ (2.5988×10¹¹ cu mi).^[19]

Published values[edit]

This table summarizes the accepted values of the Earth’s radius.

Agency	Description	Value (in meters)	Ref
IAU	nominal “zero tide” equatorial	6378100	[1]
IAU	nominal “zero tide” polar	6356800	[1]
IUGG	equatorial radius	6378137	[2]
IUGG	semiminor axis (b)	6356752.3141	[2]
IUGG	polar radius of curvature (c)	6399593.6259	[2]
IUGG	mean radius (R1)	6371008.7714	[2]
IUGG	radius of sphere of same surface (R2)	6371007.1810	[2]
IUGG	radius of sphere of same volume (R3)	6371000.7900	[2]
IERS	WGS-84 ellipsoid, semi-major axis (a)	6378137.0	[6]
IERS	WGS-84 ellipsoid, semi-minor axis (b)	6356752.3142	[6]
IERS	WGS-84 ellipsoid, polar radius of curvature (c)	6399593.6258	[6]
IERS	WGS-84 ellipsoid, Mean radius of semi-axes (R1)	6371008.7714	[6]
IERS	WGS-84 ellipsoid, Radius of Sphere of Equal Area (R2)	6371007.1809	[6]
IERS	WGS-84 ellipsoid, Radius of Sphere of Equal Volume (R3)	6371000.7900	[6]
	GRS 80 semi-major axis (a)	6378137.0
	GRS 80 semi-minor axis (b)	≈6356752.314140
	Spherical Earth Approx. of Radius (RE)	6366707.0195	[20]
	meridional radius of curvature at the equator	6335439
	Maximum (the summit of Chimborazo)	6384400	[17]
	Minimum (the floor of the Arctic Ocean)	6352800	[17]
	Average distance from center to surface	6371230±10	[18]

History[edit]

The first published reference to the Earth’s size appeared around 350 BC, when Aristotle reported in his book On the Heavens^[21] that mathematicians had guessed the circumference of the Earth to be 400,000 stadia. Scholars have interpreted Aristotle’s figure to be anywhere from highly accurate^[22] to almost double the true value.^[23] The first known scientific measurement and calculation of the circumference of the Earth was performed by Eratosthenes in about 240 BC. Estimates of the accuracy of Eratosthenes’s measurement range from 0.5% to 17%.^[24] For both Aristotle and Eratosthenes, uncertainty in the accuracy of their estimates is due to modern uncertainty over which stadion length they meant.

Around 100 BC, Posidonius of Apamea recomputed Earth’s radius, and found it to be close to that by Eratosthenes,^[25] but later Strabo incorrectly attributed him a value about 3/4 of the actual size.^[26] Claudius Ptolemy around 150 AD gave empirical evidence supporting a spherical Earth,^[27] but he accepted the lesser value attributed to Posidonius. His highly influential work, the Almagest,^[28] left no doubt among medieval scholars that Earth is spherical, but they were wrong about its size.

By 1490, Christopher Colombus believed that traveling 3,000 miles west from the west coast of the Iberian peninsula would let him reach the eastern coasts of Asia.^[29] However, the 1492 enactment of that voyage brought his fleet to the Americas. The Magellan expedition (1519–1522), which was the first circumnavigation of the World, soundly demonstrated the sphericity of the Earth,^[30] and affirmed the original measurement of 40,000 km (25,000 mi) by Eratosthenes.

Around 1690, Isaac Newton and Christiaan Huygens argued that Earth was closer to an oblate spheroid than to a sphere. However, around 1730, Jacques Cassini argued for a prolate spheroid instead, due to different interpretations of the Newtonian mechanics involved.^[31] To settle the matter, the French Geodesic Mission (1735–1739) measured one degree of latitude at two locations, one near the Arctic Circle and the other near the equator. The expedition found that Newton’s conjecture was correct:^[32] the Earth is flattened at the poles due to rotation’s centrifugal force.

See also[edit]

Notes[edit]

References[edit]

External links[edit]

• Merrifield, Michael R. (2010). “ The Earth’s Radius (and exoplanets)”. Sixty Symbols. Brady Haran for the University of Nottingham.

Как вычислили длину окружности Земли 2,5 тысячи лет назад, где диаметр планеты наибольший и за сколько ее можно обойти пешком

Диаметр Земли имеет для ученых важное значение. С его помощью можно вычислить площадь нашей планеты и расстояние до ее центра, также он помогает составлять карты и проводить запуски космических летательных аппаратов. Узнаем, как вычисляются эти параметры и каковы их значения.

Основные параметры Земли

1. Диаметр по экватору – 12756 км, по полюсам – 12713 км.
2. Средний радиус – 6371 км. На таком расстоянии от поверхности находится центр ядра. Экваториальный радиус Земли – 6378 км. Расстояние к центру Земли на полюсах – 6356,5 км.
3. Окружность Земли по экватору – 40075 км, а по полюсам – 40008 км.
4. Удаление от Солнца в километрах – приблизительно 150 миллионов. Оно наиболее подходяще для формирования и поддержания жизни. Если бы орбита Земли была ближе или дальше всего на несколько миллионов километров, условия для эволюции жизни были бы намного хуже.
5. Время, за которое Земля совершает один оборот вокруг Солнца – 365 дней 5 часов 48 минут и 46 секунд. В течение 23 часов 46 минут и 4 секунды она совершает оборот вокруг своей оси. Каждые 100 лет эта скорость уменьшается на 0,017 секунд. 140 млн. лет потребуется для того, чтобы длительность суток увеличилась на час.
6. Ось вращения планеты наклонена к плоскости орбиты под углом немногим больше 23 градусов. Это обусловливает сезонность климатических условий и четкую смену времен года. Если бы ось вращения была наклонена на несколько градусов меньше или больше – на Земле создались бы менее благоприятные климатические условия, на больше части поверхности образовались бы ледники.
7. Средняя температура на Земле – примерно 15 °C.
8. Вода занимает примерно 71% всей площади. Ее масса – 1460 миллионов миллиардов тонн. Атмосфера весит в 275 раз меньше. Ее масса – немногим больше 5 квадриллионов тонн.
9. В атмосфере 21 % кислорода. Основную массу занимает азот – биологически инертный газ, его в составе атмосферы 78%.
10. Масса Земли – примерно 6*10 24 килограмма.
11. Объем планеты – 1,08*10 12 км 3 .
12. Площадь земного шара – 510 млн км 2 .
13. Плотность – 5,5 г/см 3 .
14. Наиболее близкое к нам небесное тело – Луна. Ее среднее расстояние от Земли – примерно 384 тыс. км.

Форма планеты

На вопрос, какая форма у Земли, большинство людей ответит, что шарообразная. И здесь они сделают ошибку. На планету влияют силы гравитации: огромная масса тяготеет к ядру, поэтому происходит постоянное сжатие. Наиболее сильная центробежная сила, появляющаяся из-за движения Земли вокруг собственной оси – на экваторе.

Земля является своего рода «неправильным шаром». Сжатие является причиной того, что экваториальный диаметр планеты немногим больше, чем по полюсам. Ученые определяют форму нашей планеты как близкую к «сплюснутому эллипсоиду».

Интересно, что по причине пренебрежения сжатием Земли по полюсам, эталон метра от 1795 года оказался на 200 микрон короче.

В форме планеты важна также местная топография. Конечно же, она не может в глобальном масштабе влиять на форму планеты. Так, различия между горой Эверест и Марианской впадиной составляет примерно 19 км. В глобальных масштабах эта цифра незначительна. Максимальное расстояние от центра Земли до экватора, учитывая выпуклость земной поверхности – это вершина вулкана Чимборасо, находящегося в Эквадоре.

Разница в расстоянии от центра Земли до вершины вулкана Чимборасо и горы Эверест

Что такое экватор и для чего он нужен

Под экватором следует понимать линию, перпендикулярную оси, вдоль поверхности Земли, на одинаковом расстоянии от полюсов.

Вдоль всей этой линии день равняется ночи. Правда, из-за атмосферной рефракции продолжительность дня больше на несколько минут. Два раза в год (в дни равноденствий) Солнце находится в зените, и лучи будут направляться строго перпендикулярно земной поверхности. Широта на экваторе – 0°.

Экватор имеет важнейшее значение для определения широты географического объекта. Все точки, находящиеся к югу от воображаемой линии, имеют южную широту. А объекты, располагающиеся к северу от нее, соответственно, имеют северную широту.

Как измерить длину окружности земли

Размер Земли поддается вычислению. Для измерения длины окружности Земли пользуются высокотехнологичными приборами и спутниками. Однако до появления этих изобретений приходилось пользоваться математическими методами измерений. В 18 веке ученые П. Мешен, А.М. Лежандр, Ц. Кассини использовали способ триангуляции.

Предположим, что нужно измерить дистанцию между некоторыми точками, удаленными на несколько сотен километров. Для этого нам надо построить на местности опорную сеть. Это можно сделать с помощью треугольников. Их вершинами будут места, находящиеся на высоте. На них сооружаются воображаемые пирамиды так, чтобы они направлялись на близко расположенные пункты.

Воображаемые фигуры должны быть удобными для установки угломера и вычисления градусов углов. В одном из треугольников измеряют одну сторону, пролегающую по ровной местности. Это будет базис.

Простейший способ измерения длины экватора – умножить количество километров в одном градусе на 360.

Измерение окружности начинается с треугольника, являющегося базисом. По стороне и по углам вычисляется другие стороны этой фигуры. Одна из них является также стороной смежного треугольника. Она же является исходной для определения сторон иного треугольника. В ходе математических вычислений можно найти параметры последнего треугольника. Так можно получить значение дуги меридиана. Чем длиннее дуги меридианов, тем лучше можно вычислить нужную величину – радиус нашей планеты.

Когда известна протяженность дуги меридиана, несложно посчитать, какая будет длина одного градуса. Такой метод является основой геодезии.

Как вычислить радиус и диаметр планеты

Радиус и диаметр Земли вычислить несложно. Для этого пользуются формулами d=l/π; r=½*π. Буквы означают:

• d – диаметр;
• l – протяженность окружности;
• r – радиус (линия, проложенная от центра и до любой точки на окружности);
• π – число, приблизительно равное 3,14.

Измерение окружности Земли в древние времена

О длине этой величины было известно еще в Древней Греции. Необходимые расчеты были сделаны древнегреческим математиком, астрономом, географом Эратосфеном. Ему было известно о том, что в день солнцестояния 21 июня в Сиене, находящейся за полтысячи миль от Александрии, в полдень освещалось дно колодцев, а от предметов не обнаруживалась тень. Выходит, Солнце в этом участке планеты было в зените. В Александрии ничего подобного не происходило.

В полдень летнего солнцестояния ученый измерил тень от городского обелиска (ему была известна его высота). Так было установлено, что Александрию и Сиену отделяет 7 градусов широты.

Астроном делал вычисления дальше. 7° – это примерно одна пятидесятая часть окружности, равняющейся 360°. Умножив расстояние от Сиены до Александрии на 50, у математика получилось число 25000. Стольким милям равнялась окружность Земли.

Измерение длины окружности Земли Эратосфеном

Длина окружности Земли, рассчитанная Эратосфеном, немного меньше фактической. Это объясняется не примитивностью расчетов: этот способ узнать окружность Земли достаточно точный. Во времена жизни Эратосфена никто не знал точной дистанции между этими населенными пунктами. Также ученый не принял во внимание то, что оба города расположены на двух разных меридианах.

В средние века упоминания о подобных исследованиях были запрещены церковью. Только в 16 веке кругосветное путешествие Ф. Магеллана позволило убедиться, что планета действительно имеет округлую форму, и что окружность ее действительно равна 40 тыс. км.

Сколько времени нужно, чтобы обойти вокруг Земли пешком

Зная сколько километров составляет длина окружности Земли по экватору, можно вычислить, сколько времени понадобится, чтобы обойти его пешком. Если взять за основу обычную скорость пешехода 6 километров в час, то, воспользовавшись формулой t=S/V, можно получить значение примерно 6700 часов, или 278 суток.

Столько понадобится для того, чтобы пройти пешком вокруг Земли без передышки. Если же допустить, что воображаемый пешеход будет каждый день проходить по 6 часов, то для совершения такого путешествия ему понадобится около 1110 суток, или более 3 лет.

Интересная информация об экваторе Земли

На экваторе круглогодично жаркий и влажный климат. Леса Амазонки и экваториальной Африки, Индонезии отличаются разнообразием растительного и животного мира. Днем температура колеблется между 25 и 30 градусами. Ночью не намного холоднее: настолько сильно прогревается поверхность земли солнечными лучами.

Однако экватор интересен некоторыми географическими особенностями:

• он проходит сквозь более 30 островов;
• пересекает 14 стран;
• Эквадор имеет такое название в честь экватора;
• в большинстве экваториальных государств установлены памятники и памятные знаки в честь нулевой параллели;
• недалеко города Кито располагается вулкан Каямбе высотой около 4,7 км, с белеющей от вечного льда вершиной (и это несмотря на то, что экваториальный климат отличается постоянной жарой);
• река Конго, которая течет в центре африканского материка, проходит через нулевую параллель дважды;
• поскольку в рассматриваемой области Земля обращается очень быстро, здесь легче всего запускать спутники: они быстрее набирают необходимую скорость.

Размеры Земли – одни из главных параметров в астрономии и имеет большое практическое значение. С ее помощью можно узнать диаметр и радиус Земли. Вычислить эти параметры можно, применяя несложные математические вычисления.

Источник

Радиус Земли по широте (WGS 84)

Этот калькулятор определяет радиус Земли на заданной широте, используя референц-эллипсоид WGS 84.

Калькулятор ниже определяет радиус Земли на заданной широте. В реальности, конечно, он рассчитывает радиус референц-эллипсоида WGS 84 на заданной широте, и если вы хотите освежить в голове теорию, вы можете прочитать текст под калькулятором.

Радиус Земли по широте (WGS 84)

Радиус Земли

Поскольку Земля сплющена у полюсов и выпукла у экватора, геодезия моделирует форму Земли сплющенным сфероидом. Сплющенный сфероид, или сплющенный эллипсоид — это эллипсоид вращения, полученный вращением эллипсоида вокруг его короткой оси. Это правильная геометрическая форма, которая почти точно отражает форму Земли. Сфероид, описывающий форму Земли или другого небесного тела называется референц-эллипсоидом. Референц-эллипсоид Земли обычно называют Земной эллипсоид.

Конечно, поверхность Земли имеет неправильную форму. И более точным, чем референц-эллипсоид, приближением этой формы является геоид. Геоид являлся и является важной концепцией геодезии и геофизики уже более двух сотен лет, но работать с ним гораздо труднее, чем с референц-эллипсоидом, так как он тоже имеет неправильную поверхность, зависящую от распределения земных масс.

Собственно, из-за относительной простоты, референц-эллипсоиды и используются для расчета геодезических сетей и определения координат точек в виде широты, долготы и высоты над уровнем моря. В настоящее время наиболее часто используемым референц-эллипсоидом, использующемся также в глобальной системе позиционирования (Global Positioning System — GPS), является референц-эллипсоид WGS 84.

Эллипсоид вращения можно описать всего двумя параметрами. В геодезии используется несколько параметров, но все они эквивалентны или выводятся друг из друга:

• Экваториальный радиус a (или большая полуось), и полярный радиус b (или малая полуось);
• a и первый эксцентриситет e;
• a и геометрическое (полярное) сжатие f.

WGS 84 определяет следующие параметры эллипсоида:
Большая полуось a = 6378137.0 метров
Малая полуось b = 6356752.3142 метра

Точка на поверхности эллипсоида может быть задана параметрическим уравнением кривой

Радиус эллипсоида в данной точке можно найти через теорему Пифагора

Тут есть небольшая проблема, которая заключается в том, что угол t из формулы выше является геоцентрической широтой, а координаты точки, и в частности широта, являются геодезическими, зависящими от используемой системы координат (WGS 84), are geodetic. Геодезическая широта определяется углом между плоскостью экватора и нормалью к поверхности эллипсоида, и геоцентрическая широта — углом между плоскостью экватора и линии, соединяющей точку на поверхности эллипсоида с центром эллипсоида (см. картинку).

Таким образом, чтобы найти радиус по координатам точки, нам надо от геодезической широты перейти к геоцентрической широте .

Для начала найдем тангенс касательной к нашей кривой, получив его дифференцируя уравнение кривой.

Это касательный вектор к нашей кривой, идущий вдоль линии T на рисунке.

Мы можем повернуть его на 90 градусов (y, -x)»/> и получить нормаль , которая указывает вдоль линии N.

Параметр t в выражении выше — это наша . Наклон нормали — это тангенс угла . Таким образом

Используя соотношение между тангенсом и косинусом
cos^2(alpha)=frac<1><1+tan^2(alpha)>»/>
и между тангенсом и синусом
sin^2(alpha)=frac<1><1+frac<1>>=frac<1+tan^2(alpha)>»/>,
мы можем переписать формулу для радиуса как

и заменить тангенс тангенсом

Затем, немного упростив, мы получим следующую формулу

И, наконец, формулу, приведенную в википедии

Калькулятор выше как раз и использует эту формулу.

Источник

Как измерить расстояние на карте с помощью градусной сетки?

С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.

Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.

111,3х(50° – 32°) = 111,3х16 = 1780,8 км

Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:

111,3х(50° + 32°) = 111,3х82 = 9126,6 км

Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать. Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:

Широта параллели	Длина ее дуги величиной в 1°
0°	111,3
5°	110,9
10°	109,6
15°	107,6
20°	104,6
25°	102,1
30°	96,5
35°	91,3
40°	85,4
45°	78,8
50°	71,7
55°	64,0
60°	55,8
65°	47,2
70°	38,2
75°	28,9
80°	19,4
85°	9,7
90°	0

Например, нужно найти расстояние между точками, имеющими координаты:

А – 60° с. ш, 39° з. д.
Б – 60° с. ш, 25° з. д.

Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:

39° – 25° = 14°

Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:

14°х 55,8 км = 781,2 км

Список использованных источников

Источник