Как найти радиус земли в физике - Сайт, где вы сможете решить свои вопросы

Earth radius
Cross section of Earth’s Interior
General information
Unit system	astronomy, geophysics
Unit of	distance
Symbol	R_🜨 or , ${displaystyle {mathcal {R}}_{mathrm {eE} }^{mathrm {N} }}$
Conversions
1 R_🜨 in …	… is equal to …
SI base unit	6.3781×10⁶ m^[1]
Metric system	6,357 to 6,378 km
English units	3,950 to 3,963 mi

Earth radius (denoted as R_🜨 or ) is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) (equatorial radius, denoted a) to a minimum of nearly 6,357 km (3,950 mi) (polar radius, denoted b).

A nominal Earth radius is sometimes used as a unit of measurement in astronomy and geophysics, which is recommended by the International Astronomical Union to be the equatorial value.^[1]

A globally-average value is usually considered to be 6,371 kilometres (3,959 mi) with a 0.3% variability (±10 km) for the following reasons.
The International Union of Geodesy and Geophysics (IUGG) provides three reference values: the mean radius (R₁) of three radii measured at two equator points and a pole; the authalic radius, which is the radius of a sphere with the same surface area (R₂); and the volumetric radius, which is the radius of a sphere having the same volume as the ellipsoid (R₃).^[2] All three values are about 6,371 kilometres (3,959 mi).

Other ways to define and measure the Earth’s radius involve the radius of curvature. A few definitions yield values outside the range between polar radius and equatorial radius because they include local or geoidal topography or because they depend on abstract geometrical considerations.

Introduction[edit]

Earth’s rotation, internal density variations, and external tidal forces cause its shape to deviate systematically from a perfect sphere.^[a] Local topography increases the variance, resulting in a surface of profound complexity. Our descriptions of Earth’s surface must be simpler than reality in order to be tractable. Hence, we create models to approximate characteristics of Earth’s surface, generally relying on the simplest model that suits the need.

Each of the models in common use involve some notion of the geometric radius. Strictly speaking, spheres are the only solids to have radii, but broader uses of the term radius are common in many fields, including those dealing with models of Earth. The following is a partial list of models of Earth’s surface, ordered from exact to more approximate:

The actual surface of Earth
The geoid, defined by mean sea level at each point on the real surface^[b]
A spheroid, also called an ellipsoid of revolution, geocentric to model the entire Earth, or else geodetic for regional work^[c]
A sphere

In the case of the geoid and ellipsoids, the fixed distance from any point on the model to the specified center is called “a radius of the Earth” or “the radius of the Earth at that point”.^[d] It is also common to refer to any mean radius of a spherical model as “the radius of the earth”. When considering the Earth’s real surface, on the other hand, it is uncommon to refer to a “radius”, since there is generally no practical need. Rather, elevation above or below sea level is useful.

Regardless of the model, any radius falls between the polar minimum of about 6,357 km and the equatorial maximum of about 6,378 km (3,950 to 3,963 mi). Hence, the Earth deviates from a perfect sphere by only a third of a percent, which supports the spherical model in most contexts and justifies the term “radius of the Earth”. While specific values differ, the concepts in this article generalize to any major planet.

Physics of Earth’s deformation[edit]

Rotation of a planet causes it to approximate an oblate ellipsoid/spheroid with a bulge at the equator and flattening at the North and South Poles, so that the equatorial radius a is larger than the polar radius b by approximately aq. The oblateness constant q is given by

${displaystyle q={frac {a^{3}omega ^{2}}{GM}},,}$

where ω is the angular frequency, G is the gravitational constant, and M is the mass of the planet.^[e] For the Earth 1/q ≈ 289, which is close to the measured inverse flattening 1/f ≈ 298.257. Additionally, the bulge at the equator shows slow variations. The bulge had been decreasing, but since 1998 the bulge has increased, possibly due to redistribution of ocean mass via currents.^[4]

The variation in density and crustal thickness causes gravity to vary across the surface and in time, so that the mean sea level differs from the ellipsoid. This difference is the geoid height, positive above or outside the ellipsoid, negative below or inside. The geoid height variation is under 110 m (360 ft) on Earth. The geoid height can change abruptly due to earthquakes (such as the Sumatra-Andaman earthquake) or reduction in ice masses (such as Greenland).^[5]

Not all deformations originate within the Earth. Gravitational attraction from the Moon or Sun can cause the Earth’s surface at a given point to vary by tenths of a meter over a nearly 12-hour period (see Earth tide).

Radius and local conditions[edit]

Al-Biruni’s (973–1048) method for calculation of the Earth’s radius simplified measuring the circumference compared to taking measurements from two locations distant from each other.

Given local and transient influences on surface height, the values defined below are based on a “general purpose” model, refined as globally precisely as possible within 5 m (16 ft) of reference ellipsoid height, and to within 100 m (330 ft) of mean sea level (neglecting geoid height).

Additionally, the radius can be estimated from the curvature of the Earth at a point. Like a torus, the curvature at a point will be greatest (tightest) in one direction (north–south on Earth) and smallest (flattest) perpendicularly (east–west). The corresponding radius of curvature depends on the location and direction of measurement from that point. A consequence is that a distance to the true horizon at the equator is slightly shorter in the north–south direction than in the east–west direction.

In summary, local variations in terrain prevent defining a single “precise” radius. One can only adopt an idealized model. Since the estimate by Eratosthenes, many models have been created. Historically, these models were based on regional topography, giving the best reference ellipsoid for the area under survey. As satellite remote sensing and especially the Global Positioning System gained importance, true global models were developed which, while not as accurate for regional work, best approximate the Earth as a whole.

Extrema: equatorial and polar radii[edit]

The following radii are derived from the World Geodetic System 1984 (WGS-84) reference ellipsoid.^[6] It is an idealized surface, and the Earth measurements used to calculate it have an uncertainty of ±2 m in both the equatorial and polar dimensions.^[7] Additional discrepancies caused by topographical variation at specific locations can be significant. When identifying the position of an observable location, the use of more precise values for WGS-84 radii may not yield a corresponding improvement in accuracy.^{[clarification needed]}

The value for the equatorial radius is defined to the nearest 0.1 m in WGS-84. The value for the polar radius in this section has been rounded to the nearest 0.1 m, which is expected to be adequate for most uses. Refer to the WGS-84 ellipsoid if a more precise value for its polar radius is needed.

The Earth’s equatorial radius a, or semi-major axis, is the distance from its center to the equator and equals 6,378.1370 km (3,963.1906 mi).^[8] The equatorial radius is often used to compare Earth with other planets.

The Earth’s polar radius b, or semi-minor axis, is the distance from its center to the North and South Poles, and equals 6,356.7523 km (3,949.9028 mi).

Location-dependent radii[edit]

Three different radii as a function of Earth’s latitude. R is the geocentric radius; M is the meridional radius of curvature; and N is the prime vertical radius of curvature.

Geocentric radius[edit]

The geocentric radius is the distance from the Earth’s center to a point on the spheroid surface at geodetic latitude φ:

${displaystyle R(varphi )={sqrt {frac {(a^{2}cos varphi )^{2}+(b^{2}sin varphi )^{2}}{(acos varphi )^{2}+(bsin varphi )^{2}}}}}$

where a and b are, respectively, the equatorial radius and the polar radius.

The extrema geocentric radii on the ellipsoid coincide with the equatorial and polar radii.
They are vertices of the ellipse and also coincide with minimum and maximum radius of curvature.

Radii of curvature[edit]

Principal radii of curvature[edit]

There are two principal radii of curvature: along the meridional and prime-vertical normal sections.

Meridional[edit]

In particular, the Earth’s meridional radius of curvature (in the north–south direction) at φ is:^[9]

${displaystyle M(varphi )={frac {(ab)^{2}}{{big (}(acos varphi )^{2}+(bsin varphi )^{2}{big )}^{frac {3}{2}}}}={frac {a(1-e^{2})}{(1-e^{2}sin ^{2}varphi )^{frac {3}{2}}}}={frac {1-e^{2}}{a^{2}}}N(varphi )^{3},.}$

where is the eccentricity of the earth. This is the radius that Eratosthenes measured in his arc measurement.

Prime vertical[edit]

The length PQ, called the prime vertical radius, is . The length IQ is equal to $,e^{2}N(phi )$ . .

If one point had appeared due east of the other, one finds the approximate curvature in the east–west direction.^[f]

This Earth’s prime-vertical radius of curvature, also called the Earth’s transverse radius of curvature, is defined perpendicular (orthogonal) to M at geodetic latitude φ^[g] and is:^[9]

${displaystyle N(varphi )={frac {a^{2}}{sqrt {(acos varphi )^{2}+(bsin varphi )^{2}}}}={frac {a}{sqrt {1-e^{2}sin ^{2}varphi }}},.}$

N can also be interpreted geometrically as the normal distance from the ellipsoid surface to the polar axis.^[10]
The radius of a parallel of latitude is given by .^[11]^[12]

Polar and equatorial radius of curvature[edit]

The Earth’s meridional radius of curvature at the equator equals the meridian’s semi-latus rectum:

b²/a = 6,335.439 km

The Earth’s prime-vertical radius of curvature at the equator equals the equatorial radius, N = a.

The Earth’s polar radius of curvature (either meridional or prime-vertical) is:

a²/b = 6,399.594 km

Derivation[edit]

Extended content
The principal curvatures are the roots of Equation (125) in:^[13] ${displaystyle (EG-F^{2}),kappa ^{2}-(eG+gE-2fF),kappa +(eg-f^{2})=0=det(A-kappa ,B),}$ where in the first fundamental form for a surface (Equation (112) in^[13]): ${displaystyle ds^{2}=sum _{ij}a_{ij}dw^{i}dw^{j}=E,dvarphi ^{2}+2F,dvarphi ,dlambda +G,dlambda ^{2},}$ E, F, and G are elements of the metric tensor: ${displaystyle A=a_{ij}=sum _{nu }{frac {partial r^{nu }}{partial w^{i}}}{frac {partial r^{nu }}{partial w^{j}}}=left[{begin{array}{ll}E&F\F&Gend{array}}right],}$ ${displaystyle r=[r^{1},r^{2},r^{3}]^{T}=[x,y,z]^{T}}$ , ${displaystyle w^{1}=varphi }$ , ${displaystyle w^{2}=lambda ,}$ in the second fundamental form for a surface (Equation (123) in^[13]): ${displaystyle 2D=sum _{ij}b_{ij}dw^{i}dw^{j}=e,dvarphi ^{2}+2f,dvarphi ,dlambda +g,dlambda ^{2},}$ e, f, and g are elements of the shape tensor: ${displaystyle B=b_{ij}=sum _{nu }n^{nu }{frac {partial ^{2}r^{nu }}{partial w^{i}partial w^{j}}}=left[{begin{array}{ll}e&f\f&gend{array}}right],}$ ${displaystyle n={frac {N}{\|N\|}}}$ is the unit normal to the surface at , and because ${displaystyle {frac {partial r}{partial varphi }}}$ and ${displaystyle {frac {partial r}{partial lambda }}}$ are tangents to the surface, ${displaystyle N={frac {partial r}{partial varphi }}times {frac {partial r}{partial lambda }}}$ is normal to the surface at . With for an oblate spheroid, the curvatures are ${displaystyle kappa _{1}={frac {g}{G}}}$ and ${displaystyle kappa _{2}={frac {e}{E}},,}$ and the principal radii of curvature are ${displaystyle R_{1}={frac {1}{kappa _{1}}}}$ and ${displaystyle R_{2}={frac {1}{kappa _{2}}}.}$ The first and second radii of curvature correspond, respectively, to the Earth’s meridional and prime-vertical radii of curvature. Geometrically, the second fundamental form gives the distance from to the plane tangent at .

Extended content

The principal curvatures are the roots of Equation (125) in:^[13]

${displaystyle (EG-F^{2}),kappa ^{2}-(eG+gE-2fF),kappa +(eg-f^{2})=0=det(A-kappa ,B),}$

where in the first fundamental form for a surface (Equation (112) in^[13]):

${displaystyle ds^{2}=sum _{ij}a_{ij}dw^{i}dw^{j}=E,dvarphi ^{2}+2F,dvarphi ,dlambda +G,dlambda ^{2},}$

E, F, and G are elements of the metric tensor:

${displaystyle A=a_{ij}=sum _{nu }{frac {partial r^{nu }}{partial w^{i}}}{frac {partial r^{nu }}{partial w^{j}}}=left[{begin{array}{ll}E&F\F&Gend{array}}right],}$

${displaystyle r=[r^{1},r^{2},r^{3}]^{T}=[x,y,z]^{T}}$ , ${displaystyle w^{1}=varphi }$ , ${displaystyle w^{2}=lambda ,}$

in the second fundamental form for a surface (Equation (123) in^[13]):

${displaystyle 2D=sum _{ij}b_{ij}dw^{i}dw^{j}=e,dvarphi ^{2}+2f,dvarphi ,dlambda +g,dlambda ^{2},}$

e, f, and g are elements of the shape tensor:

${displaystyle B=b_{ij}=sum _{nu }n^{nu }{frac {partial ^{2}r^{nu }}{partial w^{i}partial w^{j}}}=left[{begin{array}{ll}e&f\f&gend{array}}right],}$

${displaystyle n={frac {N}{|N|}}}$ is the unit normal to the surface at , and because
${displaystyle {frac {partial r}{partial varphi }}}$ and ${displaystyle {frac {partial r}{partial lambda }}}$ are tangents to the surface,

${displaystyle N={frac {partial r}{partial varphi }}times {frac {partial r}{partial lambda }}}$

is normal to the surface at .

With for an oblate spheroid, the curvatures are

${displaystyle kappa _{1}={frac {g}{G}}}$

and ${displaystyle kappa _{2}={frac {e}{E}},,}$

and the principal radii of curvature are

${displaystyle R_{1}={frac {1}{kappa _{1}}}}$

and ${displaystyle R_{2}={frac {1}{kappa _{2}}}.}$

The first and second radii of curvature correspond, respectively, to the Earth’s meridional and prime-vertical radii of curvature.

Geometrically, the second fundamental form gives the distance from to the plane tangent at .

Combined radii of curvature[edit]

Azimuthal[edit]

The Earth’s azimuthal radius of curvature, along an Earth normal section at an azimuth (measured clockwise from north) α and at latitude φ, is derived from Euler’s curvature formula as follows:^[14]^: 97

${displaystyle R_{mathrm {c} }={frac {1}{{dfrac {cos ^{2}alpha }{M}}+{dfrac {sin ^{2}alpha }{N}}}},.}$

Non-directional[edit]

It is possible to combine the principal radii of curvature above in a non-directional manner.

The Earth’s Gaussian radius of curvature at latitude φ is:^[14]

${displaystyle R_{mathrm {a} }(varphi )={frac {1}{sqrt {K}}}={frac {1}{2pi }}int _{0}^{2pi }R_{mathrm {c} }(alpha ),dalpha ,={sqrt {MN}}={frac {a^{2}b}{(acos varphi )^{2}+(bsin varphi )^{2}}}={frac {a{sqrt {1-e^{2}}}}{1-e^{2}sin ^{2}varphi }},.}$

Where K is the Gaussian curvature, ${displaystyle K=kappa _{1},kappa _{2}={frac {det ,B}{det ,A}}}$ .

The Earth’s mean radius of curvature at latitude φ is:^[14]^: 97

${displaystyle R_{mathrm {m} }={frac {2}{{dfrac {1}{M}}+{dfrac {1}{N}}}},!}$

Global radii[edit]

The Earth can be modeled as a sphere in many ways. This section describes the common ways. The various radii derived here use the notation and dimensions noted above for the Earth as derived from the WGS-84 ellipsoid;^[6] namely,

Equatorial radius: a = (6378.1370 km)

Polar radius: b = (6356.7523 km)

A sphere being a gross approximation of the spheroid, which itself is an approximation of the geoid, units are given here in kilometers rather than the millimeter resolution appropriate for geodesy.

Nominal radius[edit]

In astronomy, the International Astronomical Union denotes the nominal equatorial Earth radius as ${displaystyle {mathcal {R}}_{mathrm {eE} }^{mathrm {N} }}$ , which is defined to be 6,378.1 km (3,963.2 mi).^[1]^: 3 The nominal polar Earth radius is defined as ${displaystyle {mathcal {R}}_{mathrm {pE} }^{mathrm {N} }}$ = 6,356.8 km (3,949.9 mi). These values correspond to the zero Earth tide convention. Equatorial radius is conventionally used as the nominal value unless the polar radius is explicitly required.^[1]^: 4
The nominal radius serves as a unit of length for astronomy.
(The notation is defined such that it can be easily generalized for other planets; e.g., ${displaystyle {mathcal {R}}_{mathrm {pJ} }^{mathrm {N} }}$ for the nominal polar Jupiter radius.)

Arithmetic mean radius[edit]

Equatorial (a), polar (b) and arithmetic mean Earth radii as defined in the 1984 World Geodetic System revision (not to scale)

In geophysics, the International Union of Geodesy and Geophysics (IUGG) defines the Earth’s arithmetic mean radius (denoted R₁) to be^[2]

$R_{1}={frac {2a+b}{3}},!$

The factor of two accounts for the biaxial symmetry in Earth’s spheroid, a specialization of triaxial ellipsoid.
For Earth, the arithmetic mean radius is 6,371.0088 km (3,958.7613 mi).^[15]

Authalic radius[edit]

Earth’s authalic radius (meaning “equal area”) is the radius of a hypothetical perfect sphere that has the same surface area as the reference ellipsoid. The IUGG denotes the authalic radius as R₂.^[2]
A closed-form solution exists for a spheroid:^[16]

${displaystyle R_{2}={sqrt {frac {a^{2}+{frac {b^{2}}{e}}ln {left({frac {1+e}{b/a}}right)}}{2}}}={sqrt {{frac {a^{2}}{2}}+{frac {b^{2}}{2}}{frac {tanh ^{-1}e}{e}}}}={sqrt {frac {A}{4pi }}},,}$

where e² = a² − b²/a² and A is the surface area of the spheroid.

For the Earth, the authalic radius is 6,371.0072 km (3,958.7603 mi).^[15]

The authalic radius $R_{2}$ also corresponds to the radius of (global) mean curvature, obtained by averaging the Gaussian curvature, , over the surface of the ellipsoid. Using the Gauss–Bonnet theorem, this gives

${displaystyle {frac {int K,dA}{A}}={frac {4pi }{A}}={frac {1}{R_{2}^{2}}}.}$

Volumetric radius[edit]

Another spherical model is defined by the Earth’s volumetric radius, which is the radius of a sphere of volume equal to the ellipsoid. The IUGG denotes the volumetric radius as R₃.^[2]

${displaystyle R_{3}={sqrt[{3}]{a^{2}b}},.}$

For Earth, the volumetric radius equals 6,371.0008 km (3,958.7564 mi).^[15]

Rectifying radius[edit]

Another global radius is the Earth’s rectifying radius, giving a sphere with circumference equal to the perimeter of the ellipse described by any polar cross section of the ellipsoid. This requires an elliptic integral to find, given the polar and equatorial radii:

${displaystyle M_{mathrm {r} }={frac {2}{pi }}int _{0}^{frac {pi }{2}}{sqrt {{a^{2}}cos ^{2}varphi +{b^{2}}sin ^{2}varphi }},dvarphi ,.}$

The rectifying radius is equivalent to the meridional mean, which is defined as the average value of M:^[16]

${displaystyle M_{mathrm {r} }={frac {2}{pi }}int _{0}^{frac {pi }{2}}!M(varphi ),dvarphi ,.}$

For integration limits of [0,π/2], the integrals for rectifying radius and mean radius evaluate to the same result, which, for Earth, amounts to 6,367.4491 km (3,956.5494 mi).

The meridional mean is well approximated by the semicubic mean of the two axes,^{[citation needed]}

${displaystyle M_{mathrm {r} }approx left({frac {a^{frac {3}{2}}+b^{frac {3}{2}}}{2}}right)^{frac {2}{3}},,}$

which differs from the exact result by less than 1 μm (4×10⁻⁵ in); the mean of the two axes,

${displaystyle M_{mathrm {r} }approx {frac {a+b}{2}},,}$

about 6,367.445 km (3,956.547 mi), can also be used.

Topographical radii[edit]

The mathematical expressions above apply over the surface of the ellipsoid.
The cases below considers Earth’s topography, above or below a reference ellipsoid.
As such, they are topographical geocentric distances, R_t, which depends not only on latitude.

Topographical extremes[edit]

Maximum R_t: the summit of Chimborazo is 6,384.4 km (3,967.1 mi) from the Earth’s center.
Minimum R_t: the floor of the Arctic Ocean is 6,352.8 km (3,947.4 mi) from the Earth’s center.^[17]

Topographical global mean[edit]

The topographical mean geocentric distance averages elevations everywhere, resulting in a value 230 m larger than the IUGG mean radius, the authalic radius, or the volumetric radius. This topographical average is 6,371.230 km (3,958.899 mi) with uncertainty of 10 m (33 ft).^[18]

Derived quantities: diameter, circumference, arc-length, area, volume [edit]

Earth’s diameter is simply twice Earth’s radius; for example, equatorial diameter (2a) and polar diameter (2b). For the WGS84 ellipsoid, that’s respectively:

2a = 12,756.2740 km (7,926.3812 mi),
2b = 12,713.5046 km (7,899.8055 mi).

Earth’s circumference equals the perimeter length. The equatorial circumference is simply the circle perimeter: C_e=2πa, in terms of the equatorial radius, a. The polar circumference equals C_p=4m_p, four times the quarter meridian m_p=aE(e), where the polar radius b enters via the eccentricity, e=(1−b²/a²)^0.5; see Ellipse#Circumference for details.

Arc length of more general surface curves, such as meridian arcs and geodesics, can also be derived from Earth’s equatorial and polar radii.

Likewise for surface area, either based on a map projection or a geodesic polygon.

Earth’s volume, or that of the reference ellipsoid, is V = 4/3πa²b. Using the parameters from WGS84 ellipsoid of revolution, a = 6,378.137 km and b = 6356.7523142 km, V = 1.08321×10¹² km³ (2.5988×10¹¹ cu mi).^[19]

Published values[edit]

This table summarizes the accepted values of the Earth’s radius.

Agency	Description	Value (in meters)	Ref
IAU	nominal “zero tide” equatorial	6378100	^[1]
IAU	nominal “zero tide” polar	6356800	^[1]
IUGG	equatorial radius	6378137	^[2]
IUGG	semiminor axis (b)	6356752.3141	^[2]
IUGG	polar radius of curvature (c)	6399593.6259	^[2]
IUGG	mean radius (R₁)	6371008.7714	^[2]
IUGG	radius of sphere of same surface (R₂)	6371007.1810	^[2]
IUGG	radius of sphere of same volume (R₃)	6371000.7900	^[2]
IERS	WGS-84 ellipsoid, semi-major axis (a)	6378137.0	^[6]
IERS	WGS-84 ellipsoid, semi-minor axis (b)	6356752.3142	^[6]
IERS	WGS-84 ellipsoid, polar radius of curvature (c)	6399593.6258	^[6]
IERS	WGS-84 ellipsoid, Mean radius of semi-axes (R₁)	6371008.7714	^[6]
IERS	WGS-84 ellipsoid, Radius of Sphere of Equal Area (R₂)	6371007.1809	^[6]
IERS	WGS-84 ellipsoid, Radius of Sphere of Equal Volume (R₃)	6371000.7900	^[6]
	GRS 80 semi-major axis (a)	6378137.0
	GRS 80 semi-minor axis (b)	≈6356752.314140
	Spherical Earth Approx. of Radius (R_E)	6366707.0195	^[20]
	meridional radius of curvature at the equator	6335439
	Maximum (the summit of Chimborazo)	6384400	^[17]
	Minimum (the floor of the Arctic Ocean)	6352800	^[17]
	Average distance from center to surface	6371230±10	^[18]

History[edit]

The first published reference to the Earth’s size appeared around 350 BC, when Aristotle reported in his book On the Heavens^[21] that mathematicians had guessed the circumference of the Earth to be 400,000 stadia. Scholars have interpreted Aristotle’s figure to be anywhere from highly accurate^[22] to almost double the true value.^[23] The first known scientific measurement and calculation of the circumference of the Earth was performed by Eratosthenes in about 240 BC. Estimates of the accuracy of Eratosthenes’s measurement range from 0.5% to 17%.^[24] For both Aristotle and Eratosthenes, uncertainty in the accuracy of their estimates is due to modern uncertainty over which stadion length they meant.

Around 100 BC, Posidonius of Apamea recomputed Earth’s radius, and found it to be close to that by Eratosthenes,^[25] but later Strabo incorrectly attributed him a value about 3/4 of the actual size.^[26] Claudius Ptolemy around 150 AD gave empirical evidence supporting a spherical Earth,^[27] but he accepted the lesser value attributed to Posidonius. His highly influential work, the Almagest,^[28] left no doubt among medieval scholars that Earth is spherical, but they were wrong about its size.

By 1490, Christopher Colombus believed that traveling 3,000 miles west from the west coast of the Iberian peninsula would let him reach the eastern coasts of Asia.^[29] However, the 1492 enactment of that voyage brought his fleet to the Americas. The Magellan expedition (1519–1522), which was the first circumnavigation of the World, soundly demonstrated the sphericity of the Earth,^[30] and affirmed the original measurement of 40,000 km (25,000 mi) by Eratosthenes.

Around 1690, Isaac Newton and Christiaan Huygens argued that Earth was closer to an oblate spheroid than to a sphere. However, around 1730, Jacques Cassini argued for a prolate spheroid instead, due to different interpretations of the Newtonian mechanics involved.^[31] To settle the matter, the French Geodesic Mission (1735–1739) measured one degree of latitude at two locations, one near the Arctic Circle and the other near the equator. The expedition found that Newton’s conjecture was correct:^[32] the Earth is flattened at the poles due to rotation’s centrifugal force.

Notes[edit]

^ For details see figure of the Earth, geoid, and Earth tide.
^ There is no single center to the geoid; it varies according to local geodetic conditions.
^ In a geocentric ellipsoid, the center of the ellipsoid coincides with some computed center of Earth, and best models the earth as a whole. Geodetic ellipsoids are better suited to regional idiosyncrasies of the geoid. A partial surface of an ellipsoid gets fitted to the region, in which case the center and orientation of the ellipsoid generally do not coincide with the earth’s center of mass or axis of rotation.
^ The value of the radius is completely dependent upon the latitude in the case of an ellipsoid model, and nearly so on the geoid.
^ This follows from the International Astronomical Union definition rule (2): a planet assumes a shape due to hydrostatic equilibrium where gravity and centrifugal forces are nearly balanced.^[3]
^ East–west directions can be misleading. Point B, which appears due east from A, will be closer to the equator than A. Thus the curvature found this way is smaller than the curvature of a circle of constant latitude, except at the equator. West can be exchanged for east in this discussion.
^ N is defined as the radius of curvature in the plane that is normal to both the surface of the ellipsoid at, and the meridian passing through, the specific point of interest.

References[edit]

^ ^a ^b ^c ^d ^e ^f Mamajek, E. E; Prsa, A; Torres, G; et al. (2015). “IAU 2015 Resolution B3 on Recommended Nominal Conversion Constants for Selected Solar and Planetary Properties”. arXiv:1510.07674 [astro-ph.SR].
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Moritz, H. (1980). Geodetic Reference System 1980, by resolution of the XVII General Assembly of the IUGG in Canberra.
^ IAU 2006 General Assembly: Result of the IAU Resolution votes Archived 2006-11-07 at the Wayback Machine
^ Satellites Reveal A Mystery Of Large Change In Earth’s Gravity Field , Aug. 1, 2002, Goddard Space Flight Center.
^ NASA’s Grace Finds Greenland Melting Faster, ‘Sees’ Sumatra Quake, December 20, 2005, Goddard Space Flight Center.
^ ^a ^b ^c ^d ^e ^f ^g ^h “WGS84RPT.tif:Corel PHOTO-PAINT” (PDF). Retrieved 2018-10-17.
^ “Info” (PDF). earth-info.nga.mil. Archived from the original (PDF) on 2020-08-04. Retrieved 2008-12-31.
^ “Equatorial Radius of the Earth”. Numerical Standards for Fundamental Astronomy: Astronomical Constants : Current Best Estimates (CBEs). IAU Division I Working Group. 2012. Archived from the original on 2016-08-26. Retrieved 2016-08-10.
^ ^a ^b Christopher Jekeli (2016). Geometric Reference Systems in Geodesy (PDF). Ohio State University, Columbus, Ohio. Retrieved 13 May 2023.
^ Bowring, B. R. (October 1987). “Notes on the curvature in the prime vertical section”. Survey Review. 29 (226): 195–196. doi:10.1179/sre.1987.29.226.195.
^ Bomford, G. (1952). Geodesy. OCLC 489193198.
^ Christopher Jekeli (2016). Geometric Reference Systems in Geodesy (PDF). Ohio State University, Columbus, Ohio. Retrieved 13 May 2023.
^ ^a ^b ^c Lass, Harry (1950). Vector and Tensor Analysis. McGraw Hill Book Company, Inc. pp. 71–77. ISBN 9780070365209.
^ ^a ^b ^c Torge, Wolfgang (2001). Geodesy. ISBN 9783110170726.
^ ^a ^b ^c Moritz, H. (March 2000). “Geodetic Reference System 1980”. Journal of Geodesy. 74 (1): 128–133. Bibcode:2000JGeod..74..128.. doi:10.1007/s001900050278. S2CID 195290884.
^ ^a ^b Snyder, J.P. (1987). Map Projections – A Working Manual (US Geological Survey Professional Paper 1395) p. 16–17. Washington D.C: United States Government Printing Office.
^ ^a ^b ^c “Discover-TheWorld.com – Guam – POINTS OF INTEREST – Don’t Miss – Mariana Trench”. Guam.discover-theworld.com. 1960-01-23. Archived from the original on 2012-09-10. Retrieved 2013-09-16.
^ ^a ^b Frédéric Chambat; Bernard Valette (2001). “Mean radius, mass, and inertia for reference Earth models” (PDF). Physics of the Earth and Planetary Interiors. 124 (3–4): 234–253. Bibcode:2001PEPI..124..237C. doi:10.1016/S0031-9201(01)00200-X. Archived from the original (PDF) on 30 July 2020. Retrieved 18 November 2017.
^ Williams, David R. (2004-09-01), Earth Fact Sheet, NASA, retrieved 2007-03-17
^ Phillips, Warren (2004). Mechanics of Flight. John Wiley & Sons, Inc. p. 923. ISBN 0471334588.
^ Aristotle. On the Heavens. Vol. Book II 298 B. Retrieved 5 November 2017.
^
Drummond, William (1817). “On the Science of the Egyptians and Chaldeans, Part I”. The Classical Journal. 16: 159.
^
Clarke, Alexander Ross; Helmert, Friedrich Robert (1911). “Earth, Figure of the” . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 8 (11th ed.). Cambridge University Press. pp. 801–813.
^
“Eratosthenes, the Greek Scientist”. Britannica.com. 2016.
^ Posidonius, fragment 202
^ Cleomedes (in Fragment 202) stated that if the distance is measured by some other number the result will be different, and using 3,750 instead of 5,000 produces this estimation: 3,750 x 48 = 180,000; see Fischer I., (1975), Another Look at Eratosthenes’ and Posidonius’ Determinations of the Earth’s Circumference, Ql. J. of the Royal Astron. Soc., Vol. 16, p. 152.
^ Thurston, Hugh (1994). Early astronomy. New York: Springer-Verlag New York. p. 138. ISBN 0-387-94107-X.
^ “Almagest – Ptolemy (Elizabeth)”. projects.iq.harvard.edu. Retrieved 2022-11-05.
^ John Freely, Before Galileo: The Birth of Modern Science in Medieval Europe (2013), ISBN 978-1468308501
^ Nancy Smiler Levinson (2001). Magellan and the First Voyage Around the World. Houghton Mifflin Harcourt. ISBN 978-0-395-98773-5. Retrieved 31 July 2010.
^ Cassini, Jacques (1738). Méthode de déterminer si la terre est sphérique ou non (in French).
^ Levallois, Jean-Jacques (1986). “La Vie des sciences”. Gallica. pp. 277–284, 288. Retrieved 2019-05-22.

External links[edit]

Merrifield, Michael R. (2010). “ $R_{oplus }$ The Earth’s Radius (and exoplanets)”. Sixty Symbols. Brady Haran for the University of Nottingham.

Источник

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

Траектория движения тела есть окружность.
Вектор скорости всегда направлен по касательной к окружности.
Направление скорости постоянно меняется под действием центростремительного ускорения.
Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

Записать исходные данные.
Записать формулу для определения искомой величины.
Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

Радиус окружности, по которой движется автомобиль: R = 100 м.
Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

Записать исходные данные.
Определить, что нужно найти.
Записать формулу зависимости центростремительного ускорения от частоты.
Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать – как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

[spoiler title=”источники:”]

Движение по окружности с постоянной по модулю скоростью

http://skysmart.ru/articles/mathematic/radius-okruzhnosti

[/spoiler]

Источник

Радиус Земли
Иллюстрация Земли 13-го века в De sphaera mundi.
Общая информация
Система единиц	астрономия, геофизика
Единица измерения	расстояния
Символ	`R`⊕или RE { displaystyle R_ {E}}, R e EN { displaystyle { mathcal {R}} _ { mathrm {eE}} ^ { mathrm {N}}} ${ displaystyle { mathcal {R}} _ { mathrm {eE}} ^ { mathrm {N}}}$
Конверсии
1 `R`⊕в…	… равно…

Базовая единица СИ	6,3781 × 10 м
Метрическая система	от 6,357 до 6378 км
Английские единицы	от 3950 до 3963 миль

Радиус Земли – это расстояние от от центра Земли до точки на ее поверхности. Его значение колеблется от 6378 км (3963 миль) на экваторе до 6357 км (3950 миль) на полюсе. Номинальный радиус Земли иногда используется в качестве единицы измерения в астрономии и геофизике, обозначается в астрономии символом R⊕. В других контекстах он обозначается RE { displaystyle R_ {E}} R_E или иногда R e EN { displaystyle { mathcal {R}} _ { mathrm {eE}. } ^ { mathrm {N}}} ${ displaystyle { mathcal {R}} _ { mathrm {eE}} ^ { mathrm {N}}}$ .

Земля – не идеальная сфера, а примерно сплюснутый сфероид (эллипс, вращающийся вокруг своей малой оси) с большим радиусом на экваторе, чем на полюсах. Когда указан только один радиус, Международный астрономический союз (IAU) предпочитает, чтобы это был экваториальный радиус. Международный союз геодезии и геофизики (IUGG) рекомендует три значения: среднее арифметическое радиусов, измеренных на экваторе и полюсах (R 1); аутентичный радиус, который представляет собой радиус сферы с той же площадью поверхности (R 2); и объемный радиус, который представляет собой радиус сферы, имеющей такой же объем, что и эллипсоид (R 3). Все три значения составляют около 6371 км (3959 миль).

Есть много других способов определить и измерить радиус Земли. Некоторые указаны ниже. Некоторые определения дают значения за пределами диапазона между полярным радиусом и экваториальным радиусом, потому что они включают локальную или геоидальную топологию или потому, что они зависят от абстрактных геометрических соображений.

Содержание

1 Введение
- 1.1 Физика деформации Земли
- 1.2 Радиус и местные условия
2 Фиксированный радиус
- 2.1 Экваториальный радиус
- 2.2 Полярный радиус
3 В зависимости от местоположения радиусы
- 3.1 Геоцентрический радиус
  - 3.1.1 Геофизические экстремумы
- 3.2 Радиусы кривизны
  - 3.2.1 Основные сечения
    - 3.2.1.1 Меридиональный
    - 3.2.1.2 Первичный вертикальный
    - 3.2. 1.3 Частные значения
  - 3.2.2 Направленный
  - 3.2.3 Комбинации
4 Глобальные средние радиусы
- 4.1 Средний радиус
- 4.2 Аутальный радиус
- 4.3 Объемный радиус
- 4.4 Радиус выпрямления
- 4.5 Средняя кривизна
- 4.6 Среднее расстояние от центра до поверхности
5 Оскулирующая сфера
6 Опубликованные значения
7 История
8 См. Также
9 Примечания
10 Ссылки
11 Внешние ссылки

Введение

Масштабная диаграмма сжатия эталонного эллипсоида 2003 года IERS с севером вверху. Голубая область представляет собой круг. Внешний край темно-синей линии представляет собой эллипс с той же малой осью, что и окружность, и тем же эксцентриситетом, что и Земля. Красная линия представляет линию Кармана на 100 км (62 мили) над уровнем моря, а желтая область обозначает диапазон высот для МКС на низкой околоземной орбите.

Вращение Земли, вариации внутренней плотности и внешние приливные силы приводят к систематическому отклонению ее формы от идеальной сферы. Локальная топография увеличивает дисперсию, в результате чего поверхность становится очень сложной. Наши описания земной поверхности должны быть проще, чем реальность, чтобы их можно было подобрать. Таким образом, мы создаем модели, приближающие характеристики поверхности Земли, обычно полагаясь на простейшую модель, которая соответствует потребностям.

Каждая из широко используемых моделей включает в себя некоторое понятие геометрического радиуса. Строго говоря, сферы – единственные твердые тела, у которых есть радиус, но более широкое употребление термина радиус распространено во многих областях, в том числе связанных с моделями Земли. Ниже приводится частичный список моделей земной поверхности, отсортированных от точного к более приблизительному:

Фактическая поверхность Земли
геоид, определяемый средним уровнем моря. в каждой точке реальной поверхности
A сфероид, также называемый эллипсоидом вращения, геоцентрическим для моделирования всей Земли или геодезическим для региональных работ
A сфера

В случае геоида и эллипсоидов фиксированное расстояние от любой точки модели до указанного центра называется «радиусом Земли» или «радиусом Земля в этой точке ». Также принято называть любой средний радиус сферической модели «радиусом Земли». С другой стороны, при рассмотрении реальной поверхности Земли упоминание «радиуса» редко, поскольку в этом, как правило, нет практической необходимости. Скорее, полезно иметь высоту выше или ниже уровня моря.

Независимо от модели, любой радиус находится между полярным минимумом около 6 357 км и экваториальным максимумом около 6 378 км (от 3 950 до 3 963 миль). Следовательно, Земля отклоняется от идеальной сферы всего на треть процента, что поддерживает сферическую модель в большинстве контекстов и оправдывает термин «радиус Земли». Хотя конкретные значения различаются, концепции в этой статье распространяются на любую крупную планету.

Физика деформации Земли

Вращение планеты приводит к тому, что она приближается к сплющенному эллипсоиду / сфероиду. с выпуклостью на экваторе и уплощением на Северном и Южном полюсах, так что экваториальный радиус a больше полярного радиуса b примерно на aq. Константа сжатия q задается формулой

q = a 3 ω 2 GM, { displaystyle q = { frac {a ^ {3} omega ^ {2}} {GM}} ,,} ${ displaystyle д = { гидроразрыва {а ^ {3} omega ^ {2}} {GM}} ,,}$

где ω – угловая частота, G – гравитационная постоянная, а M – масса планеты. Для Земли 1 / q ≈ 289, что близко к измеренному обратному сплющиванию 1 / f ≈ 298,257. Вдобавок выпуклость на экваторе медленно меняется. Выпуклость уменьшалась, но с 1998 года выпуклость увеличилась, возможно, из-за перераспределения массы океана посредством течений.

Изменение плотности и толщины коры вызывает изменение силы тяжести по поверхности и во времени, так что средний уровень моря отличается от эллипсоида. Эта разница составляет высоту геоида, положительную выше или вне эллипсоида, отрицательную ниже или внутри. Изменение высоты геоида составляет менее 110 м (360 футов) на Земле. Высота геоида может резко измениться из-за землетрясений (например, Суматра-Андаманское землетрясение ) или уменьшения ледяных масс (например, Гренландия ).

Не все деформации происходят внутри Земли. Гравитационное притяжение от Луна или Солнце могут вызвать изменение поверхности Земли в данной точке на десятые доли метра в течение почти 12-часового периода (см. Земной прилив ).

Радиус и местные условия

Метод Аль-Бируни (973–1048) для расчета радиуса Земли упростил измерение окружности по сравнению с измерениями в двух местах, удаленных друг от друга.

Учитывая местные и временные влияния на высоту поверхности, значения, определенные ниже, основаны на модели «общее назначение», уточнены в глобальном масштабе точно, насколько это возможно в пределах 5 м (16 футов) от опорного эллипсоида высоты, и в пределах 100 м (330 футов) от среднего уровня моря (если пренебречь геоид высоты).

Кроме того, радиус можно оценить по кривизне Земли в точке po внутр. Подобно тору , кривизна в точке будет наибольшей (самой узкой) в одном направлении (север-юг на Земле) и наименьшей (самой плоской) перпендикулярно (восток-запад). Соответствующий радиус кривизны зависит от местоположения и направления измерения от этой точки. Следствием этого является то, что расстояние до истинного горизонта на экваторе немного короче в направлении север / юг, чем в направлении восток-запад.

Таким образом, местные вариации ландшафта не позволяют определить единственный «точный» радиус. Можно только принять идеализированную модель. Со времени оценки Эратосфена было создано множество моделей. Исторически эти модели были основаны на региональной топографии, давая наилучший опорный эллипсоид для исследуемой области. По мере того как спутниковое дистанционное зондирование и особенно Глобальная система определения местоположения приобрели важность, были разработаны настоящие глобальные модели, которые, хотя и не столь точны для региональных исследований, но лучше всего соответствуют Земле в целом.

Фиксированный радиус

Следующие радиусы получены из стандартного эллипсоида Всемирной геодезической системы 1984 (WGS-84 ). Стандартный эллипсоид представляет собой идеализированную поверхность, и измерения Земли, используемые для ее расчета, имеют погрешность ± 2 м. как в экваториальном, так и в полярном измерениях. Дополнительные расхождения, вызванные орографическими вариациями в определенных местах, могут быть значительными. При определении положения наблюдаемого местоположения использование более точных значений для радиусов WGS-84 может не привести к соответствующему повышению точности .

Значение для экваториального радиуса определено с точностью до 0,1 м в WGS- 84. Значение полярного радиуса в этом разделе было округлено до ближайших 0,1 м, что, как ожидается, будет подходящим для большинства применений. Обратитесь к эллипсоиду WGS-84, если требуется более точное значение его полярного радиуса.

Обозначение указанного радиуса используется в формулах, приведенных в этой статье.

Экваториальный радиус

Экваториальный радиус Земли a или большая полуось – это расстояние от ее центра до экватора, равное 6,378,1370 км (3,963,1906 миль). Экваториальный радиус часто используется для сравнения Земли с другими планетами.

Полярный радиус

Полярный радиус Земли b или малая полуось – это расстояние от ее центра. к Северному и Южному полюсам и составляет 6 356,7523 км (3 949 9028 миль).

Радиусы, зависящие от местоположения

Геоцентрический радиус

Расстояние от центра Земли до точки на поверхности сфероида на геодезической широте φ составляет:

R (φ) знак равно (a 2 соз ⁡ φ) 2 + (b 2 грех ⁡ φ) 2 (a соз ⁡ φ) 2 + (b грех ⁡ φ) 2 { Displaystyle R ( varphi) = { sqrt { frac {( a ^ {2} cos varphi) ^ {2} + (b ^ {2} sin varphi) ^ {2}} {(a cos varphi) ^ {2} + (b sin varphi) ^ {2}}}}} ${ displaystyle R ( varphi) = { sqrt { frac {(a ^ {2} cos varphi) ^ {2} + (b ^ {2} sin varphi) ^ {2}} {(a cos varphi) ^ {2} + (b sin varphi) ^ {2}}}}}$

где a и b – соответственно экваториальный радиус и полярный радиус.

Геофизические экстремумы

Максимум: Вершина Чимборасо находится в 6 384,4 км (3 967,1 мили) от центра Земли.
Минимум: Пол Северный Ледовитый океан находится примерно в 6352,8 км (3947,4 мили) от центра Земли.

Радиусы кривизны

Основные секции

Есть два основных радиуса кривизна : вдоль меридионального и прямолинейно-вертикального нормальных участков. Кривизны являются корнями уравнения (125) в:

(EG – F 2) κ 2 – (e G + g E – 2 f F) κ + (eg – f 2) = 0 = det (A – κ В), { Displaystyle (EG-F ^ {2}) , kappa ^ {2} – (eG + gE-2fF) , kappa + (eg-f ^ {2}) = 0 = det (A- kappa , B),} ${ displaystyle (EG-F ^ {2}) , kappa ^ {2} - (например, + gE -2fF) , каппа + (например-е ^ {2}) = 0 = det (A- kappa , B),}$

где в первой фундаментальной форме для поверхности (Уравнение (112) in):

ds 2 = ∑ ijaijdwidwj = E d φ 2 + 2 F d φ d λ + G d λ 2, { displaystyle ds ^ {2} = sum _ {ij} a_ {ij} dw ^ {i} dw ^ {j} = E , d varphi ^ {2} + 2F , d varphi , d lambda + G , d lambda ^ {2},} ${ displaystyle ds ^ {2} = sum _ {ij} a_ {ij} dw ^ {i} dw ^ {j} = E , d varphi ^ {2} + 2F , d varphi , d lambda + G , d lambda ^ { 2},}$

E, F и G являются элементами метрического тензора :

A = aij = ∑ ν ∂ р ν ∂ wi ∂ r ν ∂ wj = [EFFG], { displaystyle A = a_ {ij} = sum _ { nu} { frac { partial r ^ { nu} } { partial w ^ {i}}} { frac { partial r ^ { nu}} { partial w ^ {j}}} = left [{ begin {array} {ll} EF \ FG end {array}} right],} ${ displaystyle A = a_ {ij} = sum _ { nu} { frac { partial r ^ { nu}} { partial w ^ {i}}} { frac { partial r ^ { nu}} { partial w ^ {j}} } = left [{ begin {array} {ll} EF \ FG end {array}} right],}$

r = [r 1, r 2, r 3] T = [x, y, z] T { displaystyle r = [r ^ {1}, r ^ {2}, г ^ {3}] ^ {T} = [x, y, z] ^ {T}} ${ displaystyle r = [r ^ {1}, r ^ {2}, r ^ {3}] ^ {T} = [x, y, z] ^ {T}}$ , вес 1 = φ { displaystyle w ^ {1} = varphi} ${ displaystyle w ^ {1} = varphi}$ , вес 2 знак равно λ, { displaystyle w ^ {2} = lambda,} ${ displaystyle w ^ {2} = lambda,}$

в вторая фундаментальная форма для поверхности (Уравнение (123) in):

2 D = ∑ ijbijdwidwj = ed φ 2 + 2 fd φ d λ + gd λ 2, { displaystyle 2D = сумма _ {ij} b_ {ij} dw ^ {i} dw ^ {j} = e , d varphi ^ {2} + 2f , d varphi , d lambda + g , d lambda ^ {2},} ${ displaystyle 2D = sum _ {ij} b_ {ij} dw ^ {i} dw ^ {j} = e , d varphi ^ {2} + 2f , d varphi , d lambda + g , d lambda ^ {2},}$

e, f и g – элементы тензора формы:

B = bij = ∑ ν n ν ∂ 2 r ν ∂ wi ∂ wj = [effg], { displaystyle B = b_ {ij} = sum _ { nu} n ^ { nu} { frac { partial ^ {2} r ^ { nu}} { partial w ^ {i} partial w ^ {j} }} = left [{ begin {array} {ll} e f \ f g end {array}} right],} ${ displaystyle B = b_ {ij} = sum _ { nu} n ^ { nu} { frac { partial ^ {2} r ^ { nu}} { partial w ^ {i} partial w ^ {j}}} = left [{ begin {array} {ll} e f \ f g end {array}} right], }$

n = N | N | { displaystyle n = { frac {N} {| N |}}} ${ displaystyle n = { frac {N} {| N |}}}$ – единица измерения, нормальная к поверхности в точке r { displaystyle r}, и потому ∂ р ∂ φ { displaystyle { frac { partial r} { partial varphi}}} ${ displaystyle { frac { partial r} { partial varphi}}}$ и ∂ r ∂ λ { displaystyle { frac { partial r } { partial lambda}}} ${ displaystyle { frac { partial r} { partial lambda}}}$ являются касательными к поверхности,

N = ∂ r ∂ φ × ∂ r ∂ λ { displaystyle N = { frac { partial r} { partial varphi}} times { frac { partial r} { partial lambda}}} ${ displaystyle N = { frac { partial r} { partial varphi}} times { frac { partial r} { partial lambda}}}$

нормально к поверхности в r { displaystyle r}.

с F = f = 0 { displaystyle F = f = 0}для сплющенного сфероида, кривизна равна

κ 1 = g G { displaystyle kappa _ {1} = { frac {g} {G}}} ${ displaystyle kappa _ {1} = { frac { g} {G}}}$

и κ 2 = e E, { displaystyle kappa _ {2} = { frac {e} {E}} ,,} ${ displaystyle kappa _ {2} = { frac { e} {E}} ,,}$

и радиусы кривизны равны

R 1 = 1 κ 1 { displaystyle R_ {1} = { frac {1} { kappa _ {1}}}} ${ displaystyle R_ {1} = { frac {1} { kappa _ {1} }}}$

и R 2 = 1 κ 2. { displaystyle R_ {2} = { frac {1} { kappa _ {2}}}.} ${ displaystyle R_ {2} = { frac {1} { kappa _ {2}}}.}$

Геометрически вторая фундаментальная форма дает расстояние от r + dr { displaystyle r + dr }к касательной плоскости в r { displaystyle r}.

меридиональном

В частности, радиус кривизны Земли в меридиане (север-юг) при φ:

M (φ) = R 1 = (ab) 2 ((a cos ⁡ φ) 2 + (b sin ⁡ φ) 2) 3 2 = a (1 – e 2) ( 1 – e 2 sin 2 ⁡ φ) 3 2 = 1 – e 2 a 2 N (φ) 3. { Displaystyle M ( varphi) = R_ {1} = { frac {(ab) ^ {2}} {{ big (} (a cos varphi) ^ {2} + (b sin varphi)) ^ {2} { big)} ^ { frac {3} {2}}}} = { frac {a (1-e ^ {2})} {(1-e ^ {2} sin ^ {2} varphi) ^ { frac {3} {2}}}} = { frac {1-e ^ {2}} {a ^ {2}}} N ( varphi) ^ {3} ,.} ${ displaystyle M ( varphi) = R_ {1} = { frac {(ab) ^ {2}} {{ big (} (a cos varphi) ^ {2} + (b sin varphi) ^ { 2} { big)} ^ { frac {3} {2}}}} = { frac {a (1-e ^ {2})} {(1-e ^ {2} sin ^ {2 } varphi) ^ { frac {3} {2}}}} = { frac {1-e ^ {2}} {a ^ {2}}} N ( varphi) ^ {3} ,. }$

где e { displaystyle e}– эксцентриситет земли. Это радиус, который измерил Эратосфен.

Прямая вертикаль

Если одна точка появилась точно к востоку от другой, можно найти приблизительную кривизну в направлении восток-запад.

Этот радиус кривизны в простое вертикальное, перпендикулярное (нормальное или ортогональное ) к M на геодезической широте φ:

N (φ) = R 2 = a 2 (a cos ⁡ φ) 2 + (b sin ⁡ φ) 2 знак равно a 1 – e 2 sin 2 φ. { displaystyle N ( varphi) = R_ {2} = { frac {a ^ {2}} { sqrt {(a cos varphi) ^ {2} + (b sin varphi) ^ {2 }}}} = { frac {a} { sqrt {1-e ^ {2} sin ^ {2} varphi}}} ,.} ${ displaystyle N ( varphi) = R_ {2} = { frac {a ^ {2}} { sqrt {(a cos varphi) ^ {2} + (b sin varphi) ^ {2}}}} = { frac {a} { sqrt {1-e ^ {2} sin ^ {2} varphi}}} ,.}$

Этот радиус также называется поперечным радиус кривизны . На экваторе N = R. Б. Р. Боуринг дает геометрическое доказательство того, что это перпендикулярное расстояние от поверхности до полярной оси.

Три разных радиуса в зависимости от широты Земли. R – геоцентрический радиус; M – меридиональный радиус кривизны; и N – простой вертикальный радиус кривизны.

Конкретные значения

Меридиональный радиус кривизны Земли на экваторе равен меридиану полу-широте прямой кишки :

b / a = 6,335,439 км

Полярный радиус кривизны Земли равен:

a / b = 6,399,594 км

Направленный

Радиус кривизны Земли вдоль курса с азимутом (измеряется по часовой стрелке от север) α в точке φ выводится из формулы кривизны Эйлера следующим образом:

R c = 1 cos 2 ⁡ α M + sin 2 ⁡ α N. { displaystyle R _ { mathrm {c}} = { frac {1} {{ dfrac { cos ^ {2} alpha} {M}} + { dfrac { sin ^ {2} alpha} {N}}}} ,.} ${ displaystyle R _ { mathrm {c}} = { frac {1} {{ dfrac { cos ^ {2} alpha} {M}} + { dfrac { sin ^ {2} alpha} {N}}}} ,.}$

Комбинации

Можно комбинировать указанные выше главные радиусы кривизны ненаправленным образом.

Кривизна по Гауссу составляет K = κ 1 κ 2 = det B det A { displaystyle K = kappa _ {1} , kappa _ {2} = { frac { det , B} { det , A}}} ${ displaystyle K = kappa _ {1} , kappa _ {2} = { frac { det , B} { det , A} }}$ . Гауссов радиус кривизны Земли на широте φ равен:

R a (φ) = 1 K = 1 2 π ∫ 0 2 π R c (α) d α = MN = a 2 b ( а соз ⁡ φ) 2 + (b sin ⁡ φ) 2 знак равно а 1 – е 2 1 – е 2 грех 2 ⁡ φ. { displaystyle R _ { mathrm {a}} ( varphi) = { frac {1} { sqrt {K}}} = { frac {1} {2 pi}} int _ {0} ^ {2 pi} R _ { mathrm {c}} ( alpha) , d alpha , = { sqrt {MN}} = { frac {a ^ {2} b} {(a cos varphi) ^ {2} + (b sin varphi) ^ {2}}} = { frac {a { sqrt {1-e ^ {2}}}} {1-e ^ {2} sin ^ {2} varphi}} ,.} ${ displaystyle R _ { mathrm {a}} ( varphi) = { frac {1} { sqrt {K}}} = { frac {1} {2 pi}} int _ { 0} ^ {2 pi} R _ { mathrm {c}} ( alpha) , d alpha , = { sqrt {MN}} = { frac {a ^ {2} b} {(a cos varphi) ^ {2} + (b sin varphi) ^ {2}}} = { frac {a { sqrt {1-e ^ {2}}}} {1-e ^ {2 } sin ^ {2} varphi}} ,.}$

средний радиус кривизны Земли на широте φ равен:

R m = 2 1 M + 1 N { displaystyle R _ { mathrm {m}} = { frac {2} {{ dfrac {1} {M}} + { dfrac {1} {N}}}} , !} ${ displaystyle R _ { mathrm {m}} = { frac {2} {{ dfrac {1} {M}} + { dfrac { 1} {N}}}} , !}$

Глобальные средние радиусы

Землю можно смоделировать как сферу во многих отношениях. В этом разделе описаны распространенные способы. Для различных радиусов, полученных здесь, используются обозначения и размеры, указанные выше для Земли, полученные из эллипсоида WGS-84 ; а именно,

a = Экваториальный радиус (6378,1370 км)

b = Полярный радиус (6356,7523 км)

Сфера является грубым приближением сфероида, который сам является приближением геоида, единиц здесь даны в километрах, а не в миллиметрах, подходящих для геодезии.

Средний радиус

Экваториальный (a), полярный (b) и средний радиус Земли, как определено в редакции Всемирной геодезической системы 1984 г. (без масштабирования)

В геофизике, Международный союз геодезии и геофизики (IUGG) определяет средний радиус (обозначенный R 1) как

R 1 = 2 a + b 3 { displaystyle R_ {1 } = { frac {2a + b} {3}} , !} $R_ {1} = { frac {2a + b} {3}} , !$

Для Земли средний радиус составляет 6 371,0088 км (3 958,7613 миль).

В астрономии Международный Astronomical Union обозначает номинальный экваториальный радиус Земли как R e EN { displaystyle { mathcal {R}} _ { mathrm {eE}} ^ { mathrm {N}}} ${ displaystyle { mathcal {R}} _ { mathrm {eE}} ^ { mathrm {N}}}$ , который определен как 6 378,1 км (3 963,2 мили). Номинальный полярный радиус Земли определяется как R p EN { displaystyle { mathcal {R}} _ { mathrm {pE}} ^ { mathrm {N}}} ${ displaystyle { mathcal {R}} _ { mathrm {pE}} ^ { mathrm {N}}}$ = 6 356,8 км. (3,949,9 миль). Эти значения соответствуют радиусам нулевого прилива. Экваториальный радиус обычно используется в качестве номинального значения, если полярный радиус не требуется явно.

Аутальный радиус

Ауталический радиус («равная площадь») Земли – это радиус гипотетической идеальной сферы, которая имеет та же площадь поверхности, как ссылка эллипсоида. IUGG обозначает аутентичный радиус как R 2.

. Решение в замкнутой форме существует для сфероида:

R 2 = a 2 + b 2 e ln ⁡ (1 + eb / a) 2 = a 2 2 + b 2 2 tanh – 1 ⁡ ee = A 4 π, { displaystyle R_ {2} = { sqrt { frac {a ^ {2} + { frac {b ^ {2}} {e }} ln { left ({ frac {1 + e} {b / a}} right)}} {2}}} = { sqrt {{ frac {a ^ {2}} {2} } + { frac {b ^ {2}} {2}} { frac { tanh ^ {- 1} e} {e}}}} = { sqrt { frac {A} {4 pi} }} ,,} ${ displaystyle R_ {2} = { sqrt { frac {a ^ {2} + { frac {b ^ {2}} {e }} ln { left ({ frac {1 + e} {b / a}} right)}} {2}}} = { sqrt {{ frac {a ^ {2}} {2} } + { frac {b ^ {2}} {2}} { frac { tanh ^ {- 1} e} {e}}}} = { sqrt { frac {A} {4 pi} }} ,,}$

где e = a – b / a, а A – площадь поверхности сфероида.

Для Земли автоматический радиус составляет 6 371,0072 км (3 958,7603 миль).

Объемный радиус

Другая сферическая модель определяется объемным радиусом, который является радиусом сфера объемом, равным эллипсоиду. IUGG обозначает объемный радиус как R 3.

R 3 = a 2 b 3. { displaystyle R_ {3} = { sqrt [{3}] {a ^ {2} b}} ,.} ${ displaystyle R_ {3} = { sqrt [{3}] {a ^ {2} b}} ,.}$

Для Земли объемный радиус равен 6 371 0008 км (3 958,7564 мили).

Радиус выпрямления

Другой средний радиус – это радиус выпрямления, дающий сферу с окружностью, равной периметру эллипса, описываемому любым полярным поперечным сечением эллипсоида. Для этого требуется эллиптический интеграл, чтобы найти с учетом полярного и экваториального радиусов:

M r = 2 π ∫ 0 π 2 a 2 cos 2 ⁡ φ + b 2 sin 2 ⁡ φ d φ. { displaystyle M _ { mathrm {r}} = { frac {2} { pi}} int _ {0} ^ { frac { pi} {2}} { sqrt {{a ^ {2 }} cos ^ {2} varphi + {b ^ {2}} sin ^ {2} varphi}} , d varphi ,.} ${ displaystyle M _ { mathrm {r} } = { frac {2} { pi}} int _ {0} ^ { frac { pi} {2}} { sqrt {{a ^ {2}} cos ^ {2} varphi + {b ^ {2}} sin ^ {2} varphi}} , d varphi ,.}$

Радиус выпрямления эквивалентен среднему меридиональному значению, которое определяется как среднее значение M:

M r = 2 π ∫ 0 π 2 M (φ) d φ. { displaystyle M _ { mathrm {r}} = { frac {2} { pi}} int _ {0} ^ { frac { pi} {2}} ! M ( varphi) , d varphi ,.} ${ displaystyle M _ { mathrm {r}} = { frac {2} { pi}} int _ {0} ^ { frac { pi} {2}} ! M ( varphi) , d varphi ,.}$

Для пределов интегрирования [0, π / 2] интегралы для радиуса выпрямления и среднего радиуса дают один и тот же результат, который для Земли составляет 6 367,4491 км (3 956,5494 миль).

Среднее меридиональное значение хорошо аппроксимируется средним полукубическим значением двух осей,

M r ≈ (a 3 2 + b 3 2 2) 2 3, { displaystyle M _ { mathrm {r} } приблизительно left ({ frac {a ^ { frac {3} {2}} + b ^ { frac {3} {2}}} {2}} right) ^ { frac {2} {3}} ,,} ${ displaystyle M _ { mathrm {r}} приблизительно left ({ frac {a ^ { frac {3} {2}} + b ^ { frac {3} {2}}} {2}} right) ^ { frac {2} {3} } ,,}$

, который отличается от точного результата менее чем на 1 мкм (4 × 10 дюймов); среднее значение двух осей,

M r ≈ a + b 2, { displaystyle M _ { mathrm {r}} приблизительно { frac {a + b} {2}} ,,} ${ displaystyle M _ { mathrm {r}} приблизительно { frac {a + b} {2}} ,,}$

около 6367,445 км (3956,547 миль), также можно использовать.

Средняя кривизна

Средняя кривизна во всех направлениях во всех точках поверхности определяется средневзвешенной гауссовой кривизной:

R 4 = 1 2 ∫ – π 2 π 2 cos ⁡ φ R a (φ) d φ знак равно a 2 1 e 2 – 1 ln ⁡ 1 + е 1 – е. { displaystyle R_ {4} = { frac {1} {2}} int _ {- { frac { pi} {2}}} ^ { frac { pi} {2}} ! cos varphi , R _ { mathrm {a}} ( varphi) , d varphi = { frac {a} {2}} , { sqrt {{ frac {1} {e ^ {2 }}} – 1}} , ln { frac {1 + e} {1-e}}.} ${ displaystyle R_ {4} = { frac {1} {2} } int _ {- { frac { pi} {2}}} ^ { frac { pi} {2}} ! cos varphi , R _ { mathrm {a}} ( varphi) , d varphi = { frac {a} {2}} , { sqrt {{ frac {1} {e ^ {2}}} - 1}} , ln { frac {1+ e} {1-e}}.}$

Для эллипсоида WGS 84 средняя кривизна равна 6 370,994 км (3 958,752 миль).

Среднее расстояние от центра к поверхности

Большинство глобальных средние радиусы основаны на эллипсоида, который аппроксимирует геоид. Однако геоид не имеет прямого отношения к топографии поверхности. Альтернативный расчет усредняет высоту повсюду, в результате чего средний радиус на 230 м больше, чем средний радиус IUGG, автономный радиус или объемный радиус. Это среднее значение составляет 6371,230 км (3958,899 миль) с погрешностью 10 м (33 фута).

Оскулирующая сфера

Лучшее локальное сферическое приближение эллипсоида в окрестности данной точки – это соприкасающаяся сфера. Его радиус равен гауссову радиусу кривизны, как указано выше, а его радиальное направление совпадает с нормальным направлением эллипсоида . Центр соприкасающейся сферы смещен от центра эллипсоида, но находится в центре кривизны для данной точки на поверхности эллипсоида. Эта концепция помогает интерпретировать измерения земных и планетарных радиозатменных элементов рефракции, а также в некоторых приложениях для навигации и наблюдения.

Опубликованные значения

В этой таблице обобщены принятые значения радиуса Земли.

Агентство	Описание	Значение (в метрах)
IAU	номинальный «нулевой прилив», экваториальный	6378100
IAU	номинальный “нулевой прилив” полярный	6356800
IUGG	экваториальный радиус	6378137
IUGG	малая полуось (b)	6356752.3141
IUGG	полярный радиус кривизны (c)	6399593.6259
IUGG	средний радиус (R 1)	6371008.7714
IUGG	радиус сферы той же поверхности (R 2)	6371007.1810
IUGG	радиус сферы того же объема (R 3)	6371000.7900
IERS	WGS-84 эллипсоид, большая полуось (а)	6378137.0
IERS	эллипсоид WGS-84, малая полуось (b)	6356752.3142
IERS	квадрат первого эксцентриситета WGS-84 (e)	0,00669437999014
IERS	эллипсоид WGS-84, полярный радиус кривизны (c)	6399593,6258
IERS	эллипсоид WGS-84, средний радиус полуосей (R 1)	6371008.7714
IERS	эллипсоид WGS-84, радиус сферы равных размеров a (R 2)	6371007.1809
IERS	эллипсоид WGS-84, радиус сферы равного объема (R 3)	6371000.7900
	GRS 80 большая полуось (a)	6378137.0
	GRS 80 Малая полуось (b)	≈6356752.314140
	Сферическая Земля Прибл. радиуса (R E)	6366707.0195
	меридиональный радиус кривизны на экваторе	6335439
	Максимум (вершина Чимборасо)	6384400
	Минимум (пол Северный Ледовитый океан)	6352800
	Среднее расстояние от центра до поверхности	6371230 ± 10

История

Первое опубликованное упоминание о размере Земли появилось около 350 г. До н.э., когда Аристотель сообщил в своей книге На небесах, что математики предположили, что окружность Земли составляет 400000 стадий. Ученые интерпретировали цифру Аристотеля как от очень точного до почти двойного истинного значения. Первое известное научное измерение и расчет длины окружности Земли было выполнено Эратосфеном примерно в 240 г. до н.э. Оценка точности диапазона измерений Эратосфена от 0,5% до 17%. И для Аристотеля, и для Эратосфена неопределенность в точности их оценок связана с современной неопределенностью какую длину стадиона они имели в виду.

См. Также

Окружность Земли
Масса Земли
Эффективный радиус Земли
Геодезия
Географическое расстояние
История геодезии
Шаблон: Радиус Земли

Примечания

Ссылки

Внешние ссылки

Меррифилд, Майкл Р. (2010). “R ⊕ { displaystyle R _ { oplus}} $R _ { oplus}$ Радиус Земли (и экзопланет)”. Шестьдесят символов. Брэди Харан для Ноттингемского университета.

Источник

Радиус Земли
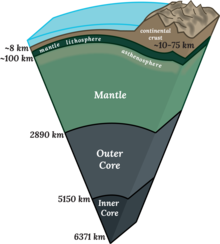
Поперечное сечение недр Земли
Общая информация
Система единиц	астрономия , геофизика
Единица	расстояние
Условное обозначение	`R` _⊕ или , ${ Displaystyle { mathcal {R}} _ { mathrm {eE}} ^ { mathrm {N}}}$
Конверсии
1 `R` _{⊕ дюйм} …	… равно …
Базовая единица СИ	6.3781 × 10 ⁶ м
Метрическая система	От 6,357 до 6,378 км
Английские единицы	От 3,950 до 3,963 миль

Радиус Земли (обозначается символом R _⊕ или ) – это расстояние от центра Земли до точки на ее поверхности или вблизи нее. Аппроксимируя фигуру Земли с помощью Земли сфероида , диапазонов радиуса от максимума почти 6378 км (3963 миль) ( экваториального радиуса , обозначенного ) до минимума почти 6357 км (3950 миль) ( полярный радиус , обозначенный б ).
R_E

Номинальный радиус Земли иногда используется в качестве единицы измерения в астрономии и геофизики , который рекомендован Международным астрономическим союзом , чтобы быть экваториальный значение.

Обычно считается, что глобальное среднее значение составляет 6 371 км (3 959 миль) с вариацией 0,3% (+/- 10 км) по следующим причинам. Международный союз геодезии и геофизики (МСГГ) обеспечивает три опорные значения: на средний радиус (R ₁ ) из трех радиусов , измеренных в двух точках экватора и полюса; authalic радиус , который является радиусом сферы , с одной и той же площадью поверхности (R ₂ ); и объемный радиус , который представляет собой радиус сферы, имеющей тот же объем, что и эллипсоид (R ₃ ). Все три значения составляют около 6371 км (3959 миль).

Другие способы определения и измерения радиуса Земли включают радиус кривизны . Некоторые определения дают значения за пределами диапазона между полярным радиусом и экваториальным радиусом, потому что они включают местную или геоидальную топографию или потому что они зависят от абстрактных геометрических соображений.

Вступление

Вращение Земли , изменения внутренней плотности и внешние приливные силы заставляют ее форму систематически отклоняться от идеальной сферы. Местная топография увеличивает дисперсию, в результате чего поверхность становится очень сложной. Наши описания земной поверхности должны быть проще, чем реальность, чтобы их можно было подобрать. Следовательно, мы создаем модели, приближающие характеристики поверхности Земли, обычно полагаясь на простейшую модель, которая соответствует потребностям.

Каждая из широко используемых моделей включает некоторое понятие геометрического радиуса . Строго говоря, сферы – единственные твердые тела, у которых есть радиус, но более широкое употребление термина радиус распространено во многих областях, включая те, которые имеют дело с моделями Земли. Ниже приводится частичный список моделей земной поверхности в порядке от точного к более приблизительному:

Реальная поверхность Земли
Геоид , определяется средним уровнем моря в каждой точке на реальную поверхности
Сфероид , называемый также эллипсоидом вращения, геоцентрическая модель всей Земли, или еще геодезический для региональной работы
сфера

В случае геоида и эллипсоидов фиксированное расстояние от любой точки модели до указанного центра называется «радиусом Земли» или «радиусом Земли в этой точке» . Также принято называть любой средний радиус сферической модели «радиусом земли» . С другой стороны, при рассмотрении реальной поверхности Земли упоминание «радиуса» редко, поскольку в этом, как правило, нет практической необходимости. Скорее, полезно иметь высоту выше или ниже уровня моря.

Независимо от модели, любой радиус находится между полярным минимумом около 6357 км и экваториальным максимумом около 6378 км (от 3950 до 3963 миль). Следовательно, Земля отклоняется от идеальной сферы всего на треть процента, что поддерживает сферическую модель в большинстве контекстов и оправдывает термин «радиус Земли». Хотя конкретные значения различаются, концепции в этой статье распространяются на любую крупную планету .