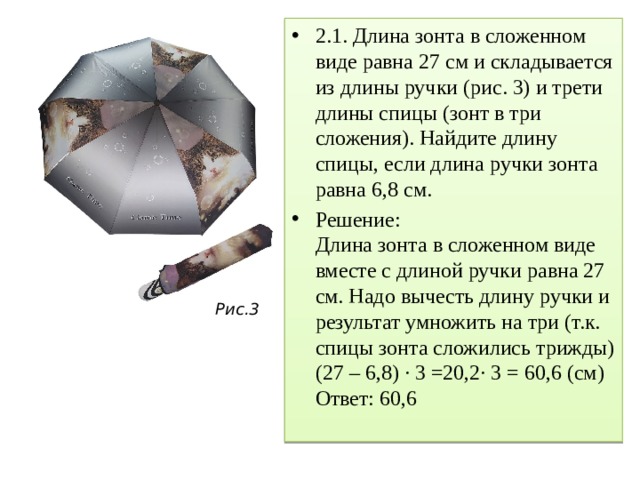
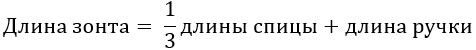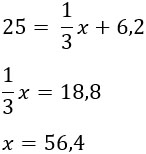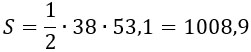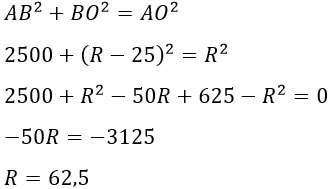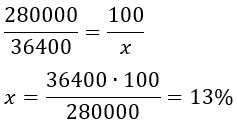В 2021 году в сборнике типовых заданий ОГЭ по математике появилась новая задача про зонт.
Вот ее текст
По этому тексту, надо ответить на 5 вопросов, которые входят в первых 5 заданий ОГЭ по математике.
Вопрос №1.
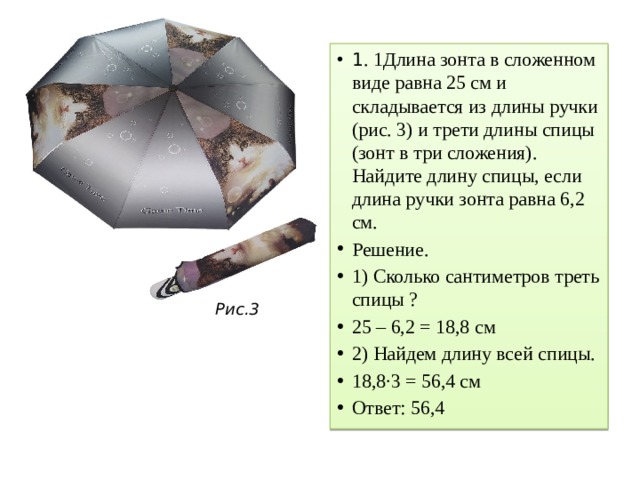
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,3 см.
Для ответа на этот вопрос. можно начертить схему, в виде отрезка, который разбит на две части, одна часть – это ручка, вторая это 1/3 часть длины спицы.
Первым действием, мы находим, сколько сантиметров, составляет 1/3 длины спицы.
Вторым действием, умножаем на 3, и получаем искомую длину спицы, которую нужно будет внести в бланк ответов.
Обратная задача из репетиционного экзамена от 28.01.2022 года:
Длина одной спицы у раскрытого зонта равна 69,6 см. При закрытии зонта спицы одновременно складываются. Длина зонта в сложенном виде равна 24,9 см, длина ручки равна 7,5 см. Во сколько раз складывается каждая спица?
Решение:
1) 24,9-7,5=17,4 (длина спицы в сложенном виде)
2)69,6:17,4=4 (в 4 раза складывается каждая спица)
Ответ 4
Вопрос №2.
Поскольку зонт сшит из треугольников, рассуждала Нина, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Нины, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 54,2 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
При ответе на этот вопрос, обратимся к тексту задачи, и найдем чему, равно основание равнобедренного треугольника а=38 см
Первым действием, мы найдем площадь равнобедренного треугольника, которая равна: половине произведения высоты на сторону к которой эта высота проведена.
Вторым действием, найдем площадь поверхности зонта. Для этого нужно площадь одного треугольника, умножить на количество треугольников из которых сшит зонт, оно равно 8 (написано в третьем предложении текста задачи). В ответе записываем значение. округленное до разряда десятков т.е. 8240.
Вопрос №3
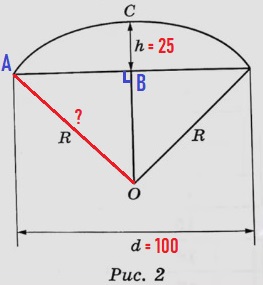
Света предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC=R. Ответ дайте в сантиметрах.
В этой задаче, на рисунке нужно было выделить прямоугольный треугольник (в нашем случае, мы его назвали ОКD), и по теореме Пифагора, 1) составили выражение, для нахождения радиуса сферы. 2) выразили из отрезка ОС и СК отрезок ОК. 3) Нашли значение КD, оно равно половине d=104, поскольку О – это центр окружности. 4) Подставили в формулу 1, и с помощью формулы сокращенного умножения, раскрыли скобку, и нашли значение R=65. Этот ответ записываем в бланк ответов.
Задача №4
Света нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2пRh , где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Светы. Число п -“пи” округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Эта задача самая простая, если вы правильно рассчитали радиус сферы R в третьем задании. Нужно только все подставить в формулу, и посчитать.
Задача №5
Рулон ткани имеет длину 24 м и ширину 150 см. На фабрике из этого рулона были вырезаны треугольные клинья для 36 зонтов, таких же, как зонт, который был у Нины и Светы. Каждый треугольник с учётом припуска на швы имеет площадь 1100 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
При внимательном прочтении задачи, понимаем, что нужно найти площадь ткани в рулоне, затем площадь материала, которое потребовалось для 36 зонтов. И найти сколько ушло ткани в обрезки.
Решение ниже:
1) Найдем площадь ткани в рулоне.
2) Найдем количество клиньев треугольников, которые вырезали из рулона ткани для 36 зонтиков. в каждом по 8 треугольников.
3) Находим сколько материала потребовалось на 288 треугольников.
4) Находим сколько материала ушло в обрезки.
5) Находим отношение между обрезками и всего материалом, составив пропорцию.
В комментариях напишите, какая из задач такого вида, для вас самая легкая, а какая сложная?
Спасибо, что прочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Прочитайте внимательно текст и выполните задания 1 — 5.


Решение: Обозначим за Х см длину спицы. Из условия известно, что треть длины спицы и ручка зонта составляют в сумме 25 см.
Составим уравнение: 1/3Х + 6,2 = 25,
1/3Х = 18,8,
Х = 18,8 * 3,
Х = 56,4 (см) — длина спицы зонта.
Ответ: 56,4.
Задание 2 (ОГЭ 2021 зонт)
Поскольку зонт сшит из треугольников, рассуждал Петя, сумму его поверхностей можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение:
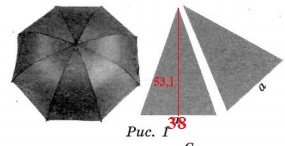
Площадь поверхности зонта состоит из 8 равных равнобедренных треугольников. Проведем высоту в треугольнике на рисунке 1. Найдем площадь одного треугольника.
S = 1/2ah = 1/2 * 38 * 53,1 = 1008,9 (кв. см).
Найдем площадь поверхности зонта.
S = 8 * 1008,9 = 8071,2 ≈ 8070 (см. кв.).
Ответ: 8070.
Задание 3 (ОГЭ 2021 зонт)
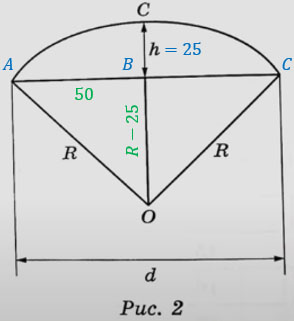
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.
Решение:
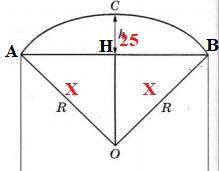
OC = R.
Рассмотрим прямоугольный треугольник AHC. Обозначим OA = x (радиус). Тогда OH = OC — HC = x — 25, AH = 50 см (половина AB из условия).
Применим теорему Пифагора.
OA2 = OH2 + AH2,
x2 = (x — 25)2 + 502,
x2 = x 2 — 50x + 625 + 2500,
50x = 3125,
x = 62,5 (см) — радиус сферы купола зонта.
Ответ: 62,5.
Задание 4 (ОГЭ 2021 зонт)
Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2ПRh, где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число П округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение: S = 2ПRh = 2 * 3,14 * 62,5 * 25 = 9812,5 ≈ 9813 (кв. см).
Ответ: 9813.
Задание 5 (ОГЭ 2021 зонт)
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение: 35 м = 3500 см.
Найдем площадь рулона ткани. S = 3500 * 80 = 280000 (кв. см).
Рассчитаем сколько ткани ушло на один зонт. 8 * 1050 = 8400 (кв. см).
8400 * 29 = 243600 (кв. см) — ткани нужно на пошив 29 зонтов.
280000 — 243600 = 36400 (кв. см) — обрезки.
Составим пропорцию для нахождения процентов ткани (x%), которая пошла на обрезки.
280000 — 100%
36400 — x%
Найдем неизвестный член пропорции.
х = (36400 * 100) / 280000 = 13%.
Ответ: 13.
Разбираем практико-ориентированные задания 1 — 5 ОГЭ (маркировка автомобильных шин) по математике 2021.
Версия для печати и копирования в MS Word
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
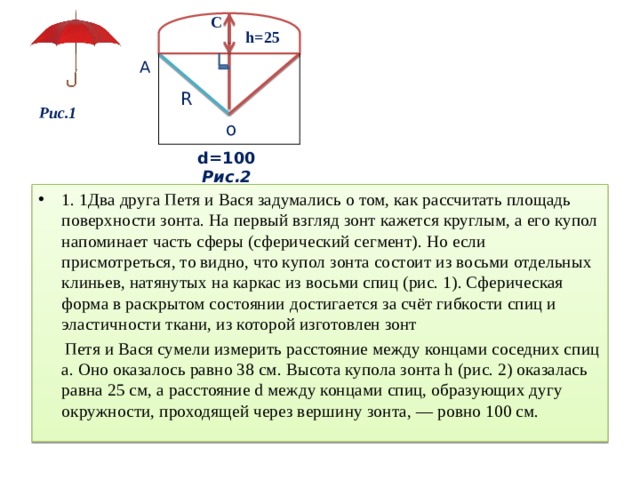
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
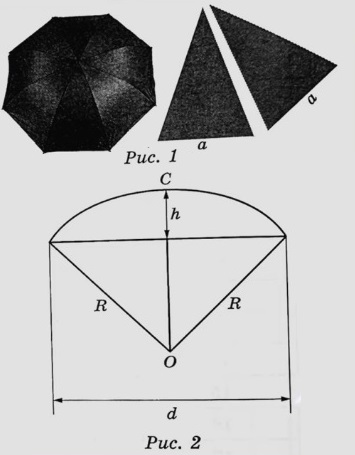
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Спрятать решение
Решение.
Из условия треть длины спицы составляет 25 − 6,2=18,8 см, следовательно, длина спицы — 56,4 см.
Ответ: 56,4.
1
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
2
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что (рис. 2). Ответ дайте в сантиметрах.
3
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число
округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
4
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 100 см.
Задание 1
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Решение
Найдём треть длины спицы, отняв от длины всего зонта длину ручки:
25 см – 6,2 см = 18,8 см
Если это треть, то вся спица в 3 раза больше:
18,8·3 = 56,4 см
Ответ: 56,4.
Задание 2
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение
По первому условию зонт состоит из 8 треугольников с основанием а = 38 см и высотой h = 53,1 см.
Площадь одного такого треугольника:
S_{Delta}=frac{1}{2}ah=frac{1}{2}cdot 38cdot 53,1=19cdot 53,1=1008,9
Найдём площадь поверхности зонта, методом Пети, округлив до ДЕСЯТКОВ:
Sповерхности = 8·SΔ = 8·1008,9 = 8071,2 ≈ 8070 см2
Ответ: 8070.
Задание 3
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.
Решение
Нам необходимо найти гипотенузу R в прямоугольном треугольнике АВО. АВ равно половине d:
AB = d/2 = 100/2 = 50
Т.к. по условию ОС = R, то:
ОВ = ОС – h = R – 25
По теореме Пифагора найдём ОА = R:
ОА2 = АВ2 + ОВ2
R2 = 502 + (R – 25)2
R2 = 2500 + R2 – 50R + 625
R2 – R2 + 50R = 3125
50R = 3125
R = 3125/50 = 62,5
Ответ: 62,5.
Задание 4
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh‚ где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение
S = 2πRh
π ≈ 3,14
R = 62,5
h = 25
Найдём площадь и округлим до целого:
S = 2πRh = 2·3,14·62,5·25 = 50·3,14·62,5 = 9812,5 ≈ 9813 см2
Ответ: 9813.
Задание 5
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение:
Найдём площадь рулона ткани в см2:
S = 35м х 80см = 3500см х 80см = 280000 см2
Помня, что в одном зонте 8 треугольников найдём сколько ушло ткани на 29 зонтов:
S1 = 29·8·1050 = 243600 см2
Найдём сколько см2 ткани рулона ушло в обрезки:
S2 = S – S1 = 280000 – 243600 = 36400 см2
Найдём сколько это процентов от начального рулона:
frac{36400}{280000}cdot 100%=frac{364}{2800}cdot 100%=frac{91}{700}cdot 100%=frac{13}{100}cdot 100%=13%
Ответ: 13.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 203
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R . Ответ дайте в сантиметрах.
Решение.
Видео 9кл.Огэ.Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R канала Тамара Остроушко
Показать
1. Длина зонта в сложенном состоянии равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Представим условие задачи в виде формулы:
Обозначим длину спицы за х, подставим все величины в формулу и решим получившееся линейное уравнение:
Ответ: 56,4.
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Площадь треугольника равна половине произведения основания и высоты, проведенной к этому основанию.
Высота дана и равна 53,1. Основание, а оно же — расстояние между концами соседних спиц, тоже дано и равно 38.
Найдем площадь одного треугольника:
Не забываем, что зонт состоит из восьми таких треугольников, их общая площадь будет равна
1008,9 · 8 = 8071,2.
Осталось округлить это число до десятков. За десятки отвечает цифра 7; после нее стоит цифра 1, значит цифра 7 остается без изменений, а все числа после нее обращаются в 0. Таким образом, 8071,2 ≈ 8070.
Ответ: 8070.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
Из условия задачи нам известны h = 25 и d = AC = 100.
Зонт — это симметричная вещица, поэтому АВ = ВС = 50.
Если ОС = R и h = 25, то ОВ = R — 25.
Рассмотрим треугольник АВО. Очевидно, что он прямоугольный. Через теорему Пифагора найдем R:
Ответ: 62,5.
4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
R = 62,5 — из предыдущей задачи;
h = 25 — высота сегмента и высота купола равны между собой.
S = 2 · 3,14 · 62,5 · 25 = 9812,5 ≈ 9813.
Ответ: 9813.
5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошла в обрезки?
Один зонт состоит из восьми треугольников, тогда 29 зонтов будут состоять из 232 треугольников.
Если на один треугольник требуется 1050 см2 ткани, то на 232 треугольника нужно будет 1050 · 232 = 243 600 см2.
Площадь ткани в рулоне равна 3500 · 80 = 280 000 см2.
Площадь ткани, ушедшей в обрезки, равна 280 000 — 243 600 = 36 400 см2.
Пусть 280 000 см2 — 100%, а 36 400 — х%. Составим и решим пропорцию:
Ответ: 13.
А вы тоже находите проблему из ничего, как Вася и Петя?)
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число
округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
1
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
2
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что (рис. 2). Ответ дайте в сантиметрах.
4
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Спрятать решение
Решение.
Воспользуемся значением R, полученным в предыдущем задании, тогда по формуле рассчитаем площадь поверхности купола
см2, округлив до целого, получим 9813 см2.
Ответ: 9813.
Решение практических задач ОГЭ. Математика. Зонт.
Учитель первой категории
МАОУ СОШ №61
Ветошкина В.А
г. Нижний Тагил
2021г.
C
h=25
А
R
Рис.1
о
d=100
Риc.2
- 1. 1Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
- 1 . 1Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
- Решение.
- 1) Сколько сантиметров треть спицы ?
- 25 – 6,2 = 18,8 см
- 2) Найдем длину всей спицы.
- 18,8∙3 = 56,4 см
- Ответ: 56,4
Рис.3
Задание 2. 1Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
- Решение.
- Высота h = 53,1 см, проведенная к основанию a = 38 см.
- Площадь каждого сегмента, равную:
- Sсег= 0,5ah
- Sсег= 0,5·38·53,1= 1008,9 см²
- Так как таких сегментов 8, то получаем полную площадь поверхности:
- 8Sсег = 8·1008,9 = 8071, 2см²
- 807/ 1 , 2 ≈ 8070
- Округляем до десятков, получаем 8070 кв. см.
- Ответ: 8070
h=53,1
a =38см
C
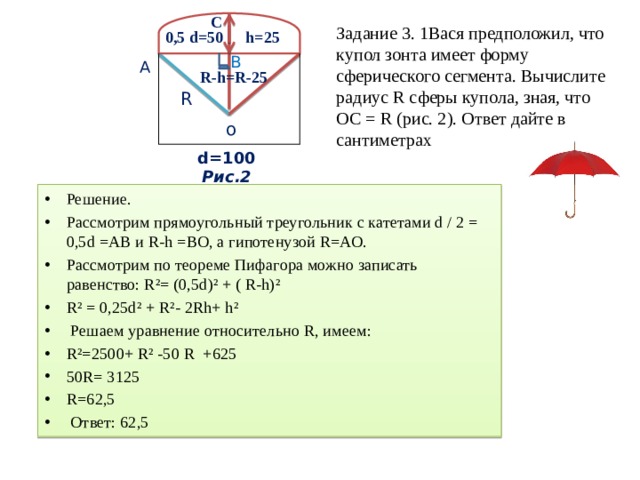
Задание 3. 1Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах
0,5 d=50
h=25
B
А
R-h=R-25
R
о
d=100
Риc.2
- Решение.
- Рассмотрим прямоугольный треугольник с катетами d / 2 = 0,5d =АВ и R-h =ВО, а гипотенузой R=АО.
- Рассмотрим по теореме Пифагора можно записать равенство: R²= (0,5d)² + ( R-h)²
- R² = 0,25d² + R²- 2Rh+ h²
- Решаем уравнение относительно R, имеем:
- R²=2500+ R² -50 R +625
- 50R= 3125
- R=62,5
- Ответ: 62,5
Задание 4. 1Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh , где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
- Решение. Подставим в формулу площади купола зонта числовые значения, получим:
- 𝑆 поверх. купола = 2πRh
- Значение R возьмём из задания №3. R = 62,5 см. h = 25 см, тогда S = 2· 3,14 ∙62,5 ∙25= 9812,5 ( см ² )
- Результат округлим до целого 9812/ ,5 ≈ 9813
- Ответ: 9813
Задание 5. 1Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
- Решение. Вычислим площадь ткани в кв. см, получим: S = 3500∙80 = 280 000 см²
- Площадь клиньев для 29 зонтов, равна:
- S= 29∙8∙1050 = 243 600 см²
- Площадь обрезков: 280 000 – 243 600 =
= 36 400 см²
- Что составляет: 36400 : 280000∙ 100%=13 .
- Ответ: 13
C
h=27
А
B
R
о
Рис.1
d=108
Риc.2
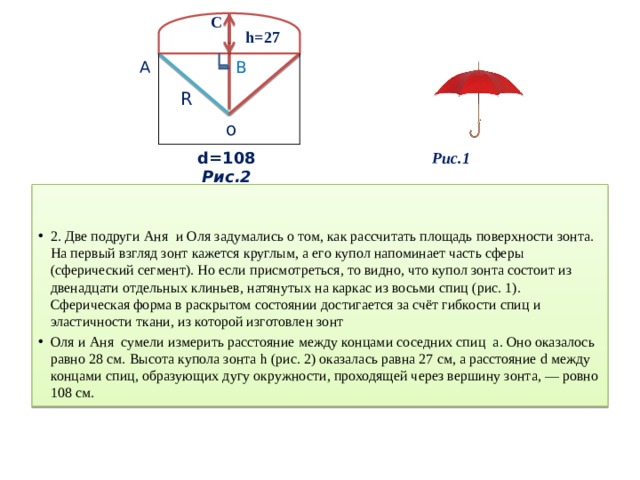
- 2. Две подруги Аня и Оля задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт
- Оля и Аня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 108 см.
- 2.1. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.
- Решение: Длина зонта в сложенном виде вместе с длиной ручки равна 27 см. Надо вычесть длину ручки и результат умножить на три (т.к. спицы зонта сложились трижды) (27 – 6,8) · 3 =20,2∙ 3 = 60,6 (см) Ответ: 60,6
Рис.3
Задание №2 Поскольку зонт сшит из треугольников, рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
- Решение: h=59 см а = 28см Зонт сшит из 12 треугольников
- 𝑆 пов .= 0,5 𝑎·ℎ ∙ 12
- 𝑆 пов .= 0,5 𝑎·ℎ ∙ 12= = 0,5 ·28·59 ∙ 12 = 9912 ( см ² )
- Результат округлим до десятков 991/ 2 ≈ 9910 Ответ: 9910.
h = 59cм
а =28см
C
Задание №3 Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС= R (рис. 2). Ответ дайте в сантиметрах
h=27
54
B
А
R
R-27
о
d=108
Риc.2
- Решение.
- Рассмотрим прямоугольный треугольник с катетами d / 2 = 0,5d= 54 и R-h = R-27, а гипотенузой R.
- Рассмотрим по теореме Пифагора можно записать равенство:
- R²= (0,5d)² + ( R-h)²
- R² = 54² + R²- 2R·27 +27²
- Решаем уравнение относительно R, имеем:
- R²= 2916 + R² -54 R +729
- 54R= 3645
- R=67,5
- Ответ: 67,5
Задание №4 Аня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R- радиус сферы, а h-высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
- Решение : 𝑆 поверх. купола = 2πRh Значение R возьмём из задания №3. R = 67,5 см. h = 27 см, тогда S = 2· 3,14 ∙67,5 ∙27=11445,3( см 2 ) Результат округлим до целого 11445/ ,3 ≈ 11445 Ответ: 11445
Задание №5 Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Ани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
- Решение: Длина рулона ткани а=20м =2000см Ширина ткани b=90см. 1)Площадь рулона ткани S рулона= a·b S рулона= a·b = 2000·90 = 180000 ( см ² ) 2)Площадь ткани на все треугольники, а их 12 S всех треугольников = 850∙12·15= 153000(см ²) 180000 – 153000 =27000 кв.см 3) 180000 см² — 100% 27000 см² — Х% Х= 27000∙100 :180000 = 15% Ответ: 15
Литература
- Типовые экзаменационные варианты. Математика. ОГЭ 36 вариантов под редакцией И.В. Ященко, М. 2021 Сайт ФИПИ.
- Типовые экзаменационные варианты. Математика. ОГЭ 50 вариантов под редакцией И.В. Ященко, М. 2020 Сайт ФИПИ.
- Типовые экзаменационные варианты. Математика. ОГЭ 50 вариантов под редакцией И.В. Ященко, М. 2021 Сайт ФИПИ.
Магометова Х.Н. МБОУ СОШ№1 с. Кизля
ОГЭ – 2021, 1-5 задания.
Задача про зонт.
Две подруги Оля и Аня задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
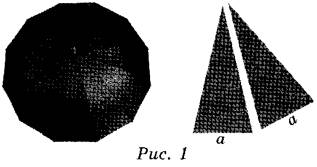
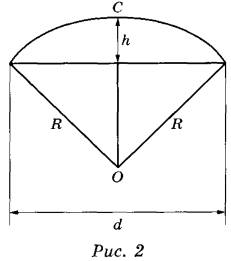
Оля и Аня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 108 см.
Задание 1. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.

Треть спицы будет равна
27 – 6,8 = 20,2 см
следовательно, длина всей спицы:
20,2∙3 = 60,6 см
Ответ: 60,6
Задание 2. Поскольку зонт сшит из треугольников, рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.Решение.
Высота h = 59 см, проведенная к основанию a = 28 см, дает площадь каждого сегмента, равную:
Так как таких сегментов 12, то получаем полную площадь поверхности:
кв. см
Округляем до десятков, получаем 9910 кв. см.
Ответ: 9910
Задание 3. Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.Решение.
Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.
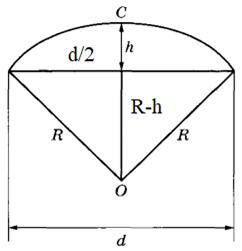
По теореме Пифагора можно записать равенство:
Решаем уравнение относительно R, имеем:
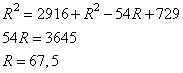
Ответ: 67,5
Задание 4. Аня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение.Подставим в формулу площади купола зонта числовые значения, получим:
Округляем до целого, имеем: 11445 см. кв.
Ответ: 11445
Задание 5. Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Ани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение.
Вычислим площадь ткани в кв. см, получим:
S = 20∙100∙90 = 180 000 см. кв.
Площадь клиньев для 15 зонтов, равна:
15∙12∙850 = 153 000 см. кв.
Площадь обрезков:
180 000 – 153 000 = 27 000 см. кв.
Что составляет:
Ответ: 15
Задача про теплицу.
Сергей Петрович решил построить на дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 6 м каждая и покрытие для обтяжки.
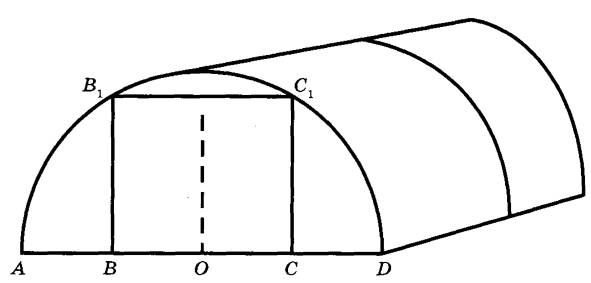
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником ВСС1В1, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 60 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение.
Вся длина теплицы составляет 6 м = 600 см. Разделим эту длину на 80 см и округлим результат до ближайшего наибольшего целого, получим:
то есть, нужно заказать 8 дуг + 1 первая дуга = 9 дуг.
Ответ: 9.
Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
Решение.
В теплице 3 грядки, между которыми будут дорожки, т.е. всего две дорожки. Длина каждой дорожки равна длине теплицы – 600 см, а ширина – 60 см. Площадь одной дорожки 600∙60 = 36000 см2, а двух – 2∙36000 = 72000 см2. Тротуарная плитка имеет размеры 20х20 см с площадью 400 см2. Следовательно, на дорожки необходимо
72000:400 = 180 плиток
Так как плитки продаются в упаковках по 10 штук, то необходимо купить
180:10 = 18 упаковок
Ответ: 18.
Задание 3. Найдите ширину входа в теплицу. Ответ дайте в метрах с точностью до десятых.Решение.
Ширина теплицы определяется диаметром полуокружности длиной 6 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности . Для полуокружности она будет выглядеть так:
, откуда
и ширина теплицы, равна:
м
Так как AB=BO=OC=CD по условию текста задания, то ширина входа
м
Ответ: 1,9.
Задание 4. Найдите ширину центральной грядки, если ширина узкой грядки относится к ширине центральной грядки как 3:4. Ответ дайте в сантиметрах с точностью до целых.
Решение.
Условно представим теплицу с грядками: две по краям с шириной см и одна центральная с шириной x см. Между ними дорожки шириной 60 см.
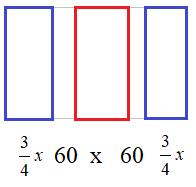
Учитывая, что вся ширина теплицы примерно 3,8 м = 380 см, получаем уравнение:
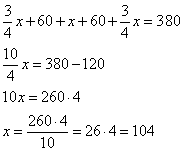
То есть, ширина центральной грядки примерно 104 см.
Ответ: 104.
Задание 5. Сколько процентов составляет площадь, отведённая под грядки, от площади всего участка, отведённого под теплицу? Ответ округлите до целых.
Решение.
Площадь, занимаемая грядками, равна:
см2,
а площадь всей теплицы:
см2.
Отношение этих площадей, равно:
,
то есть, грядки занимают примерно 68% от площади всей теплицы.
Ответ: 68.
Задачи про квартиры.
Прочитайте внимательно текст и выполните задания 1 — 5. На рисунке изображен план трехкомнатной квартиры в многоэтажном жилом доме.
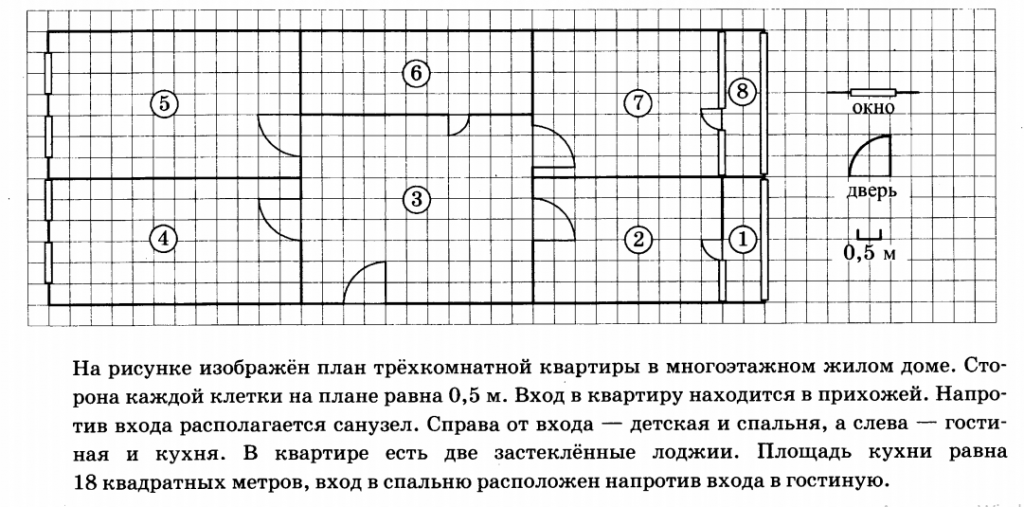
Задание 1 (ОГЭ 2020)

Решение: Из текста описания к задаче ясно, что детская комната на плане обозначена цифрой 2. Гостиная (5) расположена напротив спальни (7), а кухня (4) напротив детской. Прихожая на плане трехкомнатной квариры обозначена цифрой 3.
Ответ: 25437.
Задание 2 (ОГЭ 2020)
Найдите длину остекления лоджии в спальне. Ответ дайте в метрах.
Решение: Длина лоджии в спальне на плане равна 7 клеткам. Длина одной клетки составляет 0,5 м. 0,5 * 7 = 3,5 (м).
Ответ: 3,5 м.
Задание 3 (план трехкомнатной квартиры)

Решение: Найдем площадь пола в гостиной. 7 * 12 * 0,5 * 0,5 = 21(кв. м)
Площадь одной паркетной доски. 100 * 25 = 2500(кв. см) = 0,25(кв. м).
21 : 0,25 = 84 (шт.) плитки нужно, чтобы выложить пол в гостиной.
84 : 5 = 16,8. Нужно 17 упаковок паркетной доски.
Ответ: 17.
Задания 1 — 5 ОГЭ 2020 прототипы — подробное решение.
Задание 4 (ОГЭ 2020)
Найдите площадь, которую занимает прихожая. Ответ дайте в квадратных метрах.
Решение: На рисунке, изображенного в описании к задаче, плана трехкомнатной квартиры прихожая обозначена цифрой 3. Найдем площадь прихожей, для этого подсчитаем количество клеток, то есть 11 * 9 = 99.
Площадь одной клетки составляет: 0,5 * 0,5 = 0,25 (кв. м).
Площадь гостиной равна: 99 * 0,25 = 24,75 (кв. м).
Ответ: 24,75.
Задание 5 (ОГЭ 2020)
На сколько процентов площадь спальни (без лоджии) меньше площади кухни?
Решение:
Решаем данную задачу с помощью пропорции.
Для этого найдем площади спальни и кухни. Площадь кухни будем брать за 100%.
-
12 * 6 = 72 — площадь кухни на плане,
-
9 * 7 = 63 — площадь спальни на рисунке.
Составим пропорцию.
72 — 100%
63 — х%
Найдем неизвестный член пропорции.
х = 6300 / 72 = 87,5 (%) — спальня.
100% — 87,5% = 12,5% — на столько процентов спальня меньше кухни.
Ответ: 12,5.
Задача про шины.
Для маркировки автомобильных шин применяется единая система обозначений (см. рис. 1). Первое число означает ширину В шины (ширину протектора) в миллиметрах (см. рис. 2). Второе число — отношение высоты боковины Н к ширине шины В в процентах.

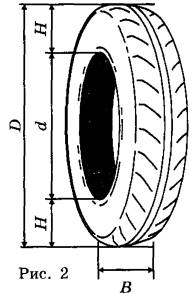
Последующая буква указывает конструкцию шины. Например, буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса в дюймах (в одном дюйме 25,4 мм). По сути, это диаметр d внутреннего отверстия в шине. Таким образом, общий диаметр колеса D легко найти, зная диаметр диска й высоту боковины.
Возможны дополнительные маркировки, означающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие.
Завод производит легковые автомобили определённой модели и устанавливает на них шины с маркировкой 185/60 R15. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
|
Диаметр диска (дюймы) Ширина шины |
14 |
15 |
16 |
17 |
|
175 |
175/70 |
175/65 |
Не разр. |
Не разр. |
|
185 |
185/70 |
185/60 |
185/55 |
Не разр. |
|
195 |
195/65 |
195/60 |
195/50, 195/55 |
195/45 |
|
205 |
205/60 |
205/55 |
205/50 |
205/45 |
|
215 |
Не разр. |
Не разр. |
215/45 |
215/40 |
Задание 1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам? Ответ дайте в миллиметрах.
Решение.
Из таблицы видно, что при диаметре 16 дюймов наименьшая ширина шины равна 185 мм (первое число до дроби).
Ответ: 185
Задание 2. На сколько миллиметров радиус колеса с маркировкой 175/65 R15 больше, чем радиус колеса с маркировкой 205/55 R15?
Решение.
Сначала вычислим диаметры колес с указанными маркировками. Для маркировки 175/65 R15, имеем:
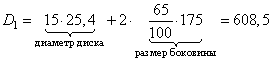
а для маркировки 205/55 R15
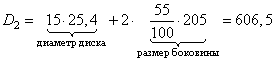
Получаем разность в радиусах колес:
мм
Ответ: 1.
Задание 3. Найдите диаметр D колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.
Решение.
Завод выпускает шины с маркировкой 185/60 R15. Имеем диаметр диска 15 дюймов = 15∙25,4 = 381 мм, высоту боковины
мм
и диаметр колеса:
мм,
что составляет 60,3 см.
Ответ: 60,3.
Задание 4. На сколько миллиметров увеличится диаметр D колеса, если заменить шины, установленные на заводе, шинами с маркировкой 205/45 R17?
Решение.
Диаметр колеса D с маркировкой 205/45 R17 можно вычислить по формуле:
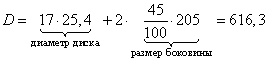
И этот диаметр больше диаметра 603 мм заводского колеса на
616,3-603 = 13,3 мм.
Ответ: 13,3
Задание 5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой 205/45 R17? Округлите результат до десятых.
Решение.
Найдем диаметр колеса с маркировкой 205/45 R17 равен 616,3 мм. Один оборот колеса с таким диаметром проходит путь, равный
мм
а с заводским диаметром 603 мм, путь
мм
Отношение этих величин дает:
то есть, пробег увеличится на 2,2%.
Ответ: 2,2.
Задача про ОСАГО.
Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу).
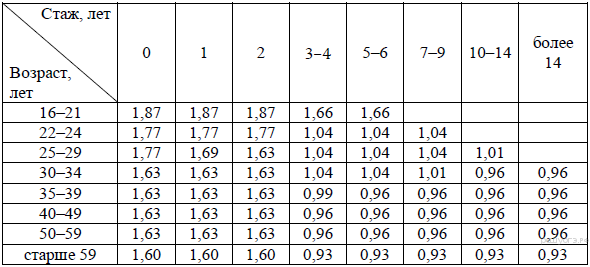
Когда Павел получил водительские права и впервые оформил полис, ему было 24 года. Чему равен КВС на начало 4-го года страхования?
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов.
Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей.
|
Класс на начало годового срока страхования |
Коэффи-циент КБМ |
Класс по окончании годового срока страхования с учётом наличия страховых случаев |
||||
|
0 страховых выплат |
1 страховая выплата |
2 страховые выплаты |
3 страховые выплаты |
4 страховые выплаты |
||
|
М |
2,45 |
0 |
М |
М |
М |
М |
|
0 |
2,3 |
1 |
М |
М |
М |
М |
|
1 |
1,55 |
2 |
М |
М |
М |
М |
|
2 |
1,4 |
3 |
1 |
М |
М |
М |
|
3 |
1 |
4 |
1 |
М |
М |
М |
|
4 |
0,95 |
5 |
2 |
1 |
М |
М |
|
5 |
0,9 |
6 |
3 |
1 |
М |
М |
|
6 |
0,85 |
7 |
4 |
2 |
М |
М |
|
7 |
0,8 |
8 |
4 |
2 |
М |
М |
|
8 |
0,75 |
9 |
5 |
2 |
М |
М |
|
9 |
0,7 |
10 |
5 |
2 |
1 |
М |
|
10 |
0,65 |
11 |
6 |
3 |
1 |
М |
|
11 |
0,6 |
12 |
6 |
3 |
1 |
М |
|
12 |
0,55 |
13 |
6 |
3 |
1 |
М |
|
13 |
0,5 |
13 |
7 |
3 |
1 |
М |
Скрыть
1
Задание 1 № 369722
Павел страховал свою гражданскую ответственность три года. В течение первого года были сделаны две страховые выплаты, после этого выплат не было.
Какой класс будет присвоен Павлу на начало четвёртого года страхования?
Решение.
В начале первого года Павлу был присвоен класс 3. После двух выплат в течение первого года на начало второго года Павлу был присвоен класс М. Поскольку в течение второго года Павел не делал страховых выплат, на начало третьего года Павлу был присвоен класс 0. В течение третьего года Павел также не делал страховых выплат, следовательно, на начало четвёртого года Павлу будет присвоен класс 1.
Ответ: 1.
2
Задание 2 № 369723
Чему равен КБМ на начало четвёртого года страхования?
Решение.
В начале первого года Павлу был присвоен класс 3. После двух выплат в течение первого года на начало второго года Павлу был присвоен класс М. Поскольку в течение второго года Павел не делал страховых выплат, на начало третьего года Павлу был присвоен класс 0. В течение третьего года Павел также не делал страховых выплат, следовательно, на начало четвёртого года Павлу будет присвоен класс 1. Из таблицы находим, что КБМ на начало четвёртого года страхования равен 1,55.
Ответ: 1,55.
3
Задание 4 № 369725
В начале третьего года страхования Павел заплатил за полис 18 745 руб. Во сколько рублей обойдётся Павлу полис на четвёртый год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
Решение.
Найдём КБМ и КВС на начало третьего года. КБМ на начало третьего года равен 2,3. КВС на начало третьего года равен 1,63. Теперь найдём составим уравнение и найдём другие коэффициенты:
КБМ на начало четвёртого года равен 1,55, КВС на начало четвёртого года равен 1,04. Значит, на начало четвёртого года стоимость полиса равна
руб.
Ответ: 8060.
4
Задание 5 № 369726
Павел въехал на участок дороги протяжённостью 2,7 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 60 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Павел въехал на участок в 11:03:16, а покинул его в 11:05:31. Нарушил ли Павел скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
Решение.
Поскольку Павел въехал на участок в 11:03:16, а покинул его в 11:05:31, он проехал расстояние в 2,7 км за 135 секунд. Переводя в часы, получаем ч. Значит, он двигался со средней скоростью в км/ч. Таким образом, Павел превысил скорость на 12 км/ч.
Ответ: 12.
Решение.
Поскольку когда Павел впервые получил права и оформил полис ему было 24 года, на начало 4-го года страхования он будет попадать в возрастную категорию 25−29 лет, а его стаж будет попадать в промежуток 3−4 года. Следовательно, КВС равен 1,04.
Ответ: 1,04.
Задача про ОСАГО
Задание 1
Павел страховал свою гражданскую ответственность три года. В течение первого года были сделаны две страховые выплаты, после этого выплат не было. Какой класс будет присвоен Павлу на начало четвёртого года страхования?
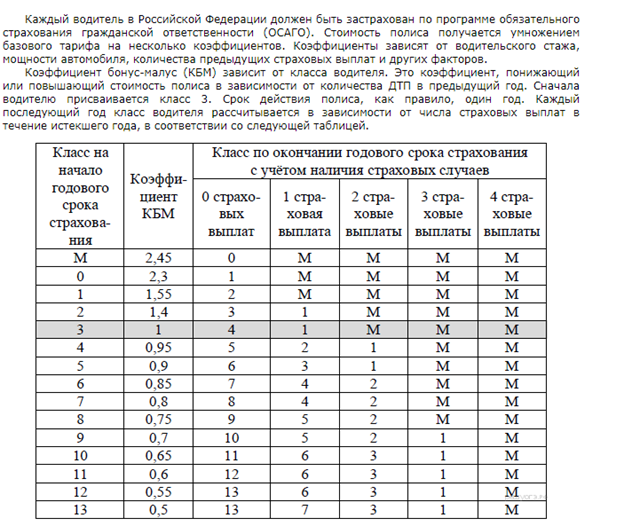
Таблица 1
Решение:
Прежде чем решать задания, прочитайте внимательно задачу. Все данные из условия запишите себе кратко, это поможет вам в решении заданий №№ 1 – 4.
Итак, работаем с таблицей 1 из условия (нам будут нужны столбцы: класс на начало, класс по окончании, учитываем число страховых случаев). Буду показывать классы стрелками разных цветов в разные годы (Таблица 2).
Павел страховал ответственность 3 года:
1 год (на начало ему присваивается 3 класс — по условию), т. к. он получил в этот год 2 страховые выплаты, то на конец 1-го и начало 2-го года ему присваивается класс М (красная стрелка в таблице)
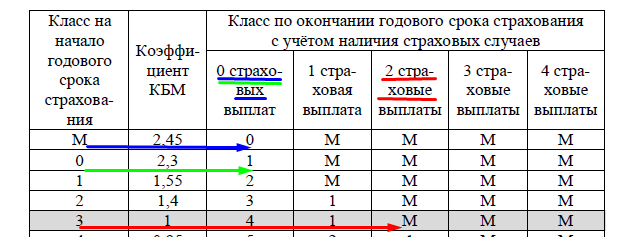
Таблица 2
2 год на начало года класс М — на конец года класс 0 (при 0 страховых выплат), синим цветом;
3 год на начало года класс 0 — на конец года класс 1 (при 0 страховых выплат), зелёным цветом. Итак, на конец 3 -го и начало 4-ого года Павлу присваивается класс 1.
Ответ: 1.
Задание 2
Чему равен КБМ на начало четвёртого года страхования?
Решение
В 1 задании мы определили, что на начало четвёртого года страхования Павлу присвоен 1 класс.
Выбираем в таблице 2 в первом столбце 1 класс и во втором столбце коэффициент КБМ, классу 1 соответствует КБМ 1,55. Это и есть ответ.
Ответ: 1,55.
Задание 3
Когда Павел получил водительские права и впервые оформил полис, ему было 24 года. Чему равен КВС на начало 4-го года страхования?
Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу 3).
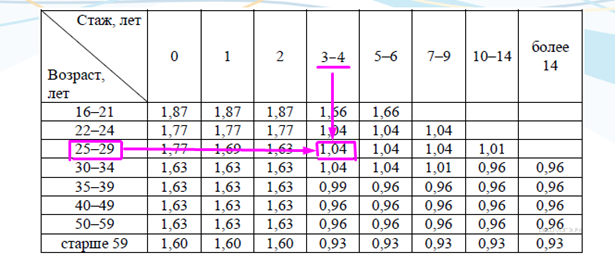
Таблица 3
Решение
Работаем с таблицей 3, в которой указан коэффициент КВС.
Работаем по такому принципу: по горизонтали смотрим стаж водителя, по вертикали — возраст водителя в тот или иной период, и на пересечении линий определяем КВС. Итак:
Через 3 года вождения (на начало 4 года), по возрасту Павел попадает в категорию 25-29 лет (24 года + 3 года), его стаж 3-4 года, и на пересечении определяем КВС 1,04. Вот и всё решение.
Ответ: 1,04.
Задание 4
В начале третьего года страхования Павел заплатил за полис 18 745 руб. Во сколько рублей обойдётся Павлу полис на четвёртый год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
Решение
Будем считать, что, если значения других коэффициентов (кроме КБМ и КВС) не изменяются, то стоимость полиса рассчитывается, как:
Стоимость полиса = Базовый тариф × КВС × КБМ
-
На начало 3 года стоимость полиса 18 745 руб., пусть х руб. — базовый тариф.
КВС = 1,63 (из таблицы 3 при стаже 2 года и возрасте 26 лет (категория 25-29);
КБМ = 2,3 (из таблицы 2, при классе 0 на начало 3 года, зелёный цвет)
Тогда, 18 745 = х × 1,63 × 2,3. Найдём х:
18 745 = 3,749х
х = 5000.
2. На начало 4 года, базовый тариф = 5000, КВС = 1,04 (задание 3), КБМ = 1,55 (задание 2). Тогда
Стоимость полиса = 5000 × 1,04 × 1,55 = 8 060 руб.
Ответ: 8 060 руб.
Задание 5
Павел въехал на участок дороги протяжённостью 2,7 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 60 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Павел въехал на участок в 11:03:16, а покинул его в 11:05:31. Нарушил ли Павел скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
Решение
В этой задаче нам не потребуются никакие коэффициенты (это обычная задача на движение).
s = 2,7 км; t1 = 11:03:16, t2 = 11:05:31, vср. — ?
1) Найдём сколько времени ехал Павел на этом участке:
t = 11:05:31 – 11:03:16 = 2 мин. 15 с = 135 с
2) Выразим время в ч, 1 ч = 60 мин. = 3600 с
135 с = 135/3600 ч = 3/80 ч
3) Найдём среднюю скорость, пользуясь формулой:
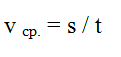

4) Таким образом, Павел превысил скорость на: 72 – 60 = 12 км/ч.
Ответ: 12 км/ч.