From Wikipedia, the free encyclopedia
In the mathematical subject of group theory, the rank of a group G, denoted rank(G), can refer to the smallest cardinality of a generating set for G, that is
If G is a finitely generated group, then the rank of G is a nonnegative integer. The notion of rank of a group is a group-theoretic analog of the notion of dimension of a vector space. Indeed, for p-groups, the rank of the group P is the dimension of the vector space P/Φ(P), where Φ(P) is the Frattini subgroup.
The rank of a group is also often defined in such a way as to ensure subgroups have rank less than or equal to the whole group, which is automatically the case for dimensions of vector spaces, but not for groups such as affine groups. To distinguish these different definitions, one sometimes calls this rank the subgroup rank. Explicitly, the subgroup rank of a group G is the maximum of the ranks of its subgroups:
Sometimes the subgroup rank is restricted to abelian subgroups.
Known facts and examples[edit]
- rank(L) − 1 ≤ 2(rank(K) − 1)(rank(H) − 1).
- This result is due to Hanna Neumann.[3][4] The Hanna Neumann conjecture states that in fact one always has rank(L) − 1 ≤ (rank(K) − 1)(rank(H) − 1). The Hanna Neumann conjecture has recently been solved by Igor Mineyev[5] and announced independently by Joel Friedman.[6]
- According to the classic Grushko theorem, rank behaves additively with respect to taking free products, that is, for any groups A and B we have
- rank(A
B) = rank(A) + rank(B).
- If
is a one-relator group such that r is not a primitive element in the free group F(x1,…, xn), that is, r does not belong to a free basis of F(x1,…, xn), then rank(G) = n.[7][8]
The rank problem[edit]
There is an algorithmic problem studied in group theory, known as the rank problem. The problem asks, for a particular class of finitely presented groups if there exists an algorithm that, given a finite presentation of a group from the class, computes the rank of that group. The rank problem is one of the harder algorithmic problems studied in group theory and relatively little is known about it. Known results include:
- The rank problem is algorithmically undecidable for the class of all finitely presented groups. Indeed, by a classical result of Adian–Rabin, there is no algorithm to decide if a finitely presented group is trivial, so even the question of whether rank(G)=0 is undecidable for finitely presented groups.[9][10]
- The rank problem is decidable for finite groups and for finitely generated abelian groups.
- The rank problem is decidable for finitely generated nilpotent groups. The reason is that for such a group G, the Frattini subgroup of G contains the commutator subgroup of G and hence the rank of G is equal to the rank of the abelianization of G.[11]
- The rank problem is undecidable for word hyperbolic groups.[12]
- The rank problem is decidable for torsion-free Kleinian groups.[13]
- The rank problem is open for finitely generated virtually abelian groups (that is containing an abelian subgroup of finite index), for virtually free groups, and for 3-manifold groups.
Generalizations and related notions[edit]
The rank of a finitely generated group G can be equivalently defined as the smallest cardinality of a set X such that there exists an onto homomorphism F(X) → G, where F(X) is the free group with free basis X. There is a dual notion of co-rank of a finitely generated group G defined as the largest cardinality of X such that there exists an onto homomorphism G → F(X). Unlike rank, co-rank is always algorithmically computable for finitely presented groups,[14] using the algorithm of Makanin and Razborov for solving systems of equations in free groups.[15][16]
The notion of co-rank is related to the notion of a cut number for 3-manifolds.[17]
If p is a prime number, then the p–rank of G is the largest rank of an elementary abelian p-subgroup.[18] The sectional p–rank is the largest rank of an elementary abelian p-section (quotient of a subgroup).
See also[edit]
- Rank of an abelian group
- Prüfer rank
- Grushko theorem
- Free group
- Nielsen equivalence
Notes[edit]
- ^ D. J. S. Robinson. A course in the theory of groups, 2nd edn, Graduate Texts in Mathematics 80 (Springer-Verlag, 1996). ISBN 0-387-94461-3
- ^ Friedhelm Waldhausen. Some problems on 3-manifolds. Algebraic and geometric topology (Proc. Sympos. Pure Math., Stanford Univ., Stanford, Calif., 1976), Part 2, pp. 313–322, Proc. Sympos. Pure Math., XXXII, Amer. Math. Soc., Providence, R.I., 1978; ISBN 0-8218-1433-8
- ^ Hanna Neumann. On the intersection of finitely generated free groups.
Publicationes Mathematicae Debrecen, vol. 4 (1956), 186–189. - ^ Hanna Neumann. On the intersection of finitely generated free groups. Addendum.
Publicationes Mathematicae Debrecen, vol. 5 (1957), p. 128 - ^ Igor Minevev,
“Submultiplicativity and the Hanna Neumann Conjecture.” Ann. of Math., 175 (2012), no. 1, 393–414. - ^ “Sheaves on Graphs and a Proof of the Hanna Neumann Conjecture”. Math.ubc.ca. Retrieved 2012-06-12.
- ^ Wilhelm Magnus, Uber freie Faktorgruppen und freie Untergruppen Gegebener Gruppen, Monatshefte für Mathematik, vol. 47(1939), pp. 307–313.
- ^ Roger C. Lyndon and Paul E. Schupp. Combinatorial Group Theory. Springer-Verlag, New York, 2001. “Classics in Mathematics” series, reprint of the 1977 edition. ISBN 978-3-540-41158-1; Proposition 5.11, p. 107
- ^ W. W. Boone.
Decision problems about algebraic and logical systems as a whole and recursively enumerable degrees of unsolvability. 1968 Contributions to Math. Logic (Colloquium, Hannover, 1966) pp. 13 33 North-Holland, Amsterdam - ^ Charles F. Miller, III. Decision problems for groups — survey and reflections. Algorithms and classification in combinatorial group theory (Berkeley, CA, 1989), pp. 1–59, Math. Sci. Res. Inst. Publ., 23, Springer, New York, 1992; ISBN 0-387-97685-X
- ^ John Lennox, and Derek J. S. Robinson. The theory of infinite soluble groups. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, Oxford, 2004. ISBN 0-19-850728-3
- ^ G. Baumslag, C. F. Miller and H. Short. Unsolvable problems about small cancellation and word hyperbolic groups. Bulletin of the London Mathematical Society, vol. 26 (1994), pp. 97–101
- ^ Ilya Kapovich, and Richard Weidmann. Kleinian groups and the rank problem. Geometry and Topology, vol. 9 (2005), pp. 375–402
- ^ John R. Stallings.
Problems about free quotients of groups. Geometric group theory (Columbus, OH, 1992), pp. 165–182, Ohio State Univ. Math. Res. Inst. Publ., 3, de Gruyter, Berlin, 1995. ISBN 3-11-014743-2 - ^ A. A. Razborov.
Systems of equations in a free group. (in Russian) Izvestia Akademii Nauk SSSR, Seriya Matematischeskaya, vol. 48 (1984), no. 4, pp. 779–832. - ^ G. S.Makanin
Equations in a free group. (Russian), Izvestia Akademii Nauk SSSR, Seriya Matematischeskaya, vol. 46 (1982), no. 6, pp. 1199–1273 - ^ Shelly L. Harvey. On the cut number of a 3-manifold. Geometry & Topology, vol. 6 (2002), pp. 409–424
- ^ Aschbacher, M. (2002), Finite Group Theory, Cambridge University Press, p. 5, ISBN 978-0-521-78675-1
РАНГ ГРУППЫ
- РАНГ ГРУППЫ
-
(общий и специальный) – понятие теории групп. Группа G имеет конечный общий р а н г r, если r – наименьшее число с тем свойством, что всякая конечно порожденная подгруппа группы Gсодержится в подгруппе, обладающей r’ образующими
 . Группа G имеет конечный специальный ранг r, если rявляется наименьшим числом с тем свойством, что всякая конечно порожденная подгруппа группы G обладает системой образующих, содержащей не более чем rэлементов. В случае, если соответствующего конечного числа не существует, общий (специальный) Р. г. считается бесконечным.
. Группа G имеет конечный специальный ранг r, если rявляется наименьшим числом с тем свойством, что всякая конечно порожденная подгруппа группы G обладает системой образующих, содержащей не более чем rэлементов. В случае, если соответствующего конечного числа не существует, общий (специальный) Р. г. считается бесконечным. Общий Р. г. меньше или равен ее специальному рангу. Существуют группы, общий ранг к-рых конечен (и даже равен двум), в то время как специальный ранг бесконечен. Такова, напр., счетная симметрич. группа. Для абелевых групп общий и специальный ранги совпадают с рангом Прюфера (см. Абелева группа).
Лит.:[1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967.
О. А. Иванова.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
Смотреть что такое “РАНГ ГРУППЫ” в других словарях:
-
РАНГ ГРУППЫ Л — и размерность любой из её подгрупп Картана, генерируемых подалгеброй Картава (см. Ли алгебра). Р. г. Ли равен рангу её алгебры Ли. Для матричных групп рангом группы является ранг матриц, образующих группу. Так как всякая группа Ли локально… … Физическая энциклопедия
-
РАНГ ГРУППЫ ЛИ — (вещественной или комплексной) размерность (соответственно вещественная или комплексная) любой из ее Картана подгрупп. Р. г. Ли равен рангу ее алгебры Ли (см. Ранг алгебры Ли). Если группа Ли G совпадает с множеством вещественных или комплексных… … Математическая энциклопедия
-
РАНГ АЛГЕБРАИЧЕСКОЙ ГРУППЫ — G размерность любой из ее Картана подгрупп (эта размерность не зависит от выбора подгруппы Картана). Наряду с Р. а. г. Gрассматриваются ее п о л у п р о с т о й р а н г и р е д у к т и в н ы й р а н г, к рые, по определению, равны соответственно… … Математическая энциклопедия
-
РАНГ — понятие, тесно связанное с понятием базиса. Обычно Р. определяется либо как минимальная из мощностей порождающего множества (так, напр., вводится б а з и с н ы й р а н г а л г е б р а и ч ес к о й с и с т е м ы), либо как максимальная мощность… … Математическая энциклопедия
-
Ранг (биологическая систематика) — В биологической систематике ранг (= таксономическая категория) уровень в иерархически организованной системе живых организмов (например, класс, отряд, семейство). Несмотря на ряд проблем с использованием рангов, они продолжают применяться,… … Википедия
-
Ранг (биология) — У этого термина существуют и другие значения, см. Ранг. В биологической систематике ранг (= таксономическая категория) уровень в иерархически организованной системе живых организмов (например, класс, отряд, семейство). Несмотря на ряд… … Википедия
-
Ранг-ранг — Боконизм (англ. Bokononism) вымышленная религия, изложенная Куртом Воннегутом в книге «Колыбель для кошки». Основоположником боконизма явлется Боконон. Боконизм открыто утверждает, что все его учения это ложь. Боконисты веруют в то, что… … Википедия
-
Ранг (таксономия) — В биологической систематике ранг (= таксономическая категория) уровень в иерархически организованной системе живых организмов (например, класс, отряд, семейство). Несмотря на ряд проблем с использованием рангов, они продолжают применяться,… … Википедия
-
Ранг — В Викисловаре есть статья «ранг» Ранг в биологической систематике уровень в иерархически организованной системе живых организмов (например … Википедия
-
Группы Ли — Группой Ли над полем K ( или ) называется группа G, снабжённая структурой дифференцируемого (гладкого) многообразия над K, причём отображения и , определённые так … Википедия
В математической теме теории групп , то ранг группы G , обозначим ранг ( G ), может относиться к наименьшей мощности в виде порождающего множества для G , то есть
Если G – конечно порожденная группа , то ранг G – неотрицательное целое число. Понятие ранга группы является теоретико-групповым аналогом понятия размерности векторного пространства . Действительно, для p -групп рангом группы P является размерность векторного пространства P / Φ ( P ), где Φ ( P ) – подгруппа Фраттини .
Ранг группы также часто определяется таким образом, чтобы гарантировать, что ранг подгрупп меньше или равен всей группе, что автоматически имеет место для размерностей векторных пространств, но не для таких групп, как аффинные группы . Чтобы различать эти различные определения, этот ранг иногда называют рангом подгруппы . Явно ранг подгруппы группы G равен максимуму рангов ее подгрупп:
Иногда ранг подгруппы ограничивается абелевыми подгруппами.
Известные факты и примеры
- Для нетривиальной группы G ранг ( G ) = 1 тогда и только тогда, когда G – циклическая группа . Тривиальная группа T имеет rank ( T ) = 0, поскольку минимальное порождающее множество T является пустым множеством .
- Для свободной абелевой группы имеем
- Если X – множество и G = F ( X ) – свободная группа со свободным базисом X, то rank ( G ) = | X |,
- Если группа H является гомоморфным образом (или фактор-группой ) группы G, то rank ( H ) ≤ rank ( G ).
- Если G конечная неабелева простая группа (например, G = A n , знакопеременная группа , для n > 4), то rank ( G ) = 2. Этот факт является следствием классификации конечных простых групп .
- Если G – конечно порожденная группа и Φ ( G ) ≤ G – подгруппа Фраттини группы G (которая всегда нормальна в G, так что фактор-группа G / Φ ( G ) определена), то rank ( G ) = rank ( G / Φ ( G )).
- Если G является фундаментальной группой замкнутого (то есть компактный и без краев) , соединенных 3-многообразие М , то ранг ( G ) ≤ г ( М ), где г ( М ) является родом Хегор из М .
- Если H , K ≤ F ( X ) – конечно порожденные подгруппы свободной группы F ( X ) такие, что пересечение нетривиально, то L конечно порождена и
- ранг ( L ) – 1 ≤ 2 (ранг ( K ) – 1) (ранг ( H ) – 1).
- Этот результат принадлежит Ханне Нойманн . Гипотеза Ханны Нойман утверждает, что на самом деле у каждого всегда есть rank ( L ) – 1 ≤ (rank ( K ) – 1) (rank ( H ) – 1). Гипотеза Ханны Нойман недавно была решена Игорем Минеевым и независимо объявлена Джоэлем Фридманом.
- Согласно классической теореме Грушко ранг ведет себя аддитивно по отношению к взятию свободных произведений , то есть для любых групп A и B имеем
- Оценка ( B ) = ранг ( ) + ранг ( Б ).
- Если это группа с одним соотношением, такая что r не является примитивным элементом в свободной группе F ( x 1 , …, x n ), то есть r не принадлежит свободному базису F ( x 1 ,. .., x n ), то rank ( G ) = n .
Проблема ранга
В теории групп изучается алгоритмическая проблема , известная как проблема ранга . Задача спрашивает для конкретного класса конечно представленных групп, существует ли алгоритм, который, учитывая конечное представление группы из этого класса, вычисляет ранг этой группы. Проблема ранга – одна из наиболее сложных алгоритмических проблем, изучаемых в теории групп, и о ней известно относительно мало. Известные результаты включают:
- Проблема ранга алгоритмически неразрешима для класса всех конечно представленных групп . Действительно, согласно классическому результату Адяна – Рабина , не существует алгоритма, позволяющего определить, является ли конечно представленная группа тривиальной, поэтому даже вопрос о том, является ли rank ( G ) = 0, неразрешимым для конечно представленных групп.
- Проблема ранга разрешима для конечных групп и конечно порожденных абелевых групп .
- Проблема ранга разрешима для конечно порожденных нильпотентных групп . Причина заключается в том, что для такой группы G , то подгруппа Фраттини из G содержит коммутант из G и , следовательно , ранг G равен рангу абелианизации из G .
- Проблема ранга неразрешима для словесных гиперболических групп .
- Проблема ранга разрешима для клейновых групп без кручения .
- Проблема ранга открыта для конечно порожденных виртуально абелевых групп (содержащих абелеву подгруппу конечного индекса ), для виртуально свободных групп и для групп трехмерных многообразий .
Обобщения и родственные понятия
Ранг конечно порожденной группы G может быть эквивалентным образом определяется как наименьшее мощности множества X , таких , что существует на гомоморфизм F ( X ) → G , где F ( X ) является свободной группой со свободным базисом X . Существует двойное понятие совместного ранга в виде конечно порожденной группы G определяется как по величине мощности из X , таких , что существует на гомоморфизм G → F ( X ). В отличие от ранга, коранг всегда алгоритмически вычислим для конечно представленных групп , используя алгоритм Маканина и Разборова для решения систем уравнений в свободных группах. Понятие коранга связано с понятием числа разреза для 3-многообразий .
Если р является простым числом , то р – ранг из G является крупнейшим Рангом элементарной абелевой р – подгруппы. Сечения р – ранг является крупнейшим рангом элементарного абелевого р -сече- (фактор подгруппы).
Смотрите также
- Ранг абелевой группы
- Прюфер ранг
- Теорема Грушко
- Бесплатная группа
- Эквивалентность Нильсена
Примечания
Функция
РАНГ(
)
, английский вариант RANK(),
возвращает
ранг числа в списке чисел. Ранг числа — это его величина относительно других значений в списке. Например, в массиве {10;20;5} число 5 будет иметь ранг 1, т.к. это наименьшее число, число 10 – ранг 2, а 20 – ранг 3 (это ранг по возрастанию, когда наименьшему значению присваивается ранг 1). Если список отсортировать, то ранг числа будет его позицией (если нет повторов).
Синтаксис
РАНГ
(
число
;
ссылка
;порядок)
Число
— число, для которого определяется ранг.
Ссылка
— ссылка на список чисел (диапазон ячеек с числами). Напрямую массив задать нельзя, формула =РАНГ(10;{10:50:30:40:50}) работать не будет. Но, если ввести формулу
=РАНГ(B7;$A$7:$A$11)
, то она будет работать (хотя ячейка
B7
– вне списка с числами). Если в
B7
содержится число вне списка с числами, то формула вернет ошибку #Н/Д.
Нечисловые значения в ссылке игнорируются. Числам, сохраненным в текстовом формате, ранг также не присваивается, функция воспринимает их как текст.
Порядок
— число, определяющее способ упорядочения.
-
Если порядок равен 0 (нулю) или опущен, то MS EXCEL присваивает ранг=1 максимальному числу, меньшим значениям присваиваются б
о
льшие ранги. -
Если порядок — любое ненулевое число, то то MS EXCEL присваивает ранг=1 минимальному числу, б
о
льшим значениям присваиваются б
о
льшие ранги.
Примечание
: Начиная с MS EXCEL 2010 для вычисления ранга также используются функции
РАНГ.СР()
и
РАНГ.РВ()
. Последняя функция аналогична
РАНГ()
.
Определяем ранг в списке без повторов
Если список чисел находится в диапазоне
A7:A11
, то формула
=РАНГ(A7;$A$7:$A$11)
определит ранг числа из ячейки
А7
(см.
файл примера
).
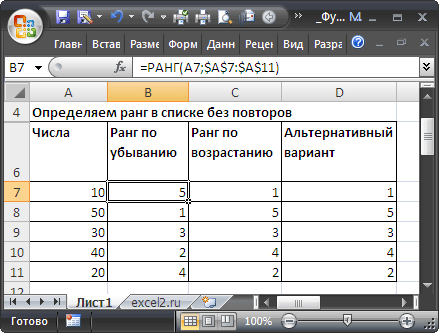
Т.к. аргумент
порядок
опущен, то MS EXCEL присвоил ранг=1 максимальному числу (50), а максимальный ранг (5 = количеству значений в списке) – минимальному (10).
Альтернативный вариант:
=СЧЁТЕСЛИ($A$7:$A$11;”>”&A7)+1
В столбце
С
приведена формула
=РАНГ(A7;$A$7:$A$11;1)
с рангом по возрастанию, ранг=1 присвоен минимальному числу. Альтернативный вариант:
=СЧЁТЕСЛИ($A$7:$A$11;”<“&A7)+1
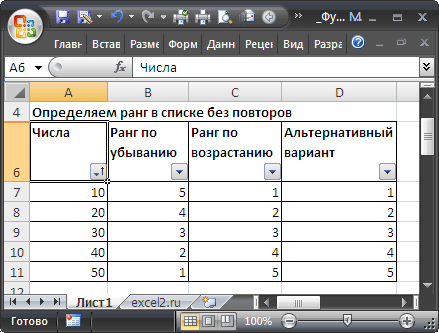
Если исходный список
отсортировать
, то ранг числа будет его позицией в списке.
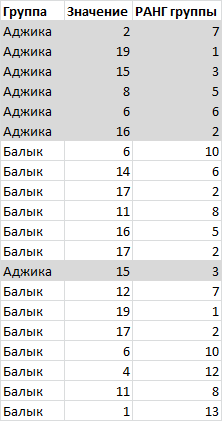
Ранг по условию
Если список состоит из значений, относящихся к разным группам (например, к разным маркам машин), то ранг можно вычислить не только относительно всей совокупности данных, но и относительно данных каждой отдельной группы.
В
файле примера
ранг по условию (условием является принадлежность значения к групп) вычислен с помощью формулы:
=СЧЁТЕСЛИМН($A$3:$A$22;A3;$B$3:$B$22;”>”&B3)+1
В столбце А содержатся названия группы, в столбце В – значения.
Связь функций
НАИБОЛЬШИЙ()
/
НАИМЕНЬШИЙ()
и
РАНГ()
Функции
НАИБОЛЬШИЙ()
и
РАНГ()
являются взаимодополняющими в том смысле, что записав формулу
=НАИБОЛЬШИЙ($A$7:$A$11;РАНГ(A7;$A$7:$A$11))
мы получим тот же исходный массив
A7:A11
.
Определяем ранг в списке с повторами
Если список содержит
повторы
, то повторяющимся значениям (выделено цветом) будет присвоен одинаковый ранг (максимальный, если использована функция
РАНГ()
или
РАНГ.РВ()
) или среднее значение, если
РАНГ.СР()
). Наличие повторяющихся чисел влияет на ранги последующих чисел. Например, если в списке целых чисел, отсортированных по возрастанию, дважды встречается число 10, имеющее ранг 5, число 11 будет иметь ранг 7 (ни одно из чисел не будет иметь ранга 6).
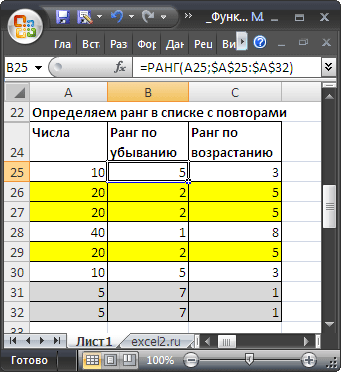
Иногда это не удобно и требуется, чтобы ранги не повторялись (например, при определении призовых мест, когда нельзя занимать нескольким людям одно место).
В этом нам поможет формула
=РАНГ(A37;A$37:A$44)+СЧЁТЕСЛИ(A$37:A37;A37)-1
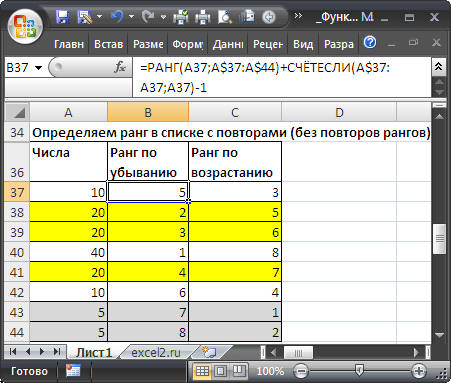
Предполагается, что исходный список с числами находится в диапазоне
А37:А44
.
Примечание
. В
MS EXCEL 2010
добавилась функция
РАНГ.РВ(число;ссылка;[порядок])
Если несколько значений имеют одинаковый ранг, возвращается наивысший ранг этого набора значений (присваивает повторяющимся числам одинаковые значения ранга). В
файле примера
дается пояснение работы этой функции. Также добавилась функция
РАНГ.СР(число;ссылка;[порядок])
Если несколько значений имеют одинаковый ранг, возвращается среднее.
Массив рангов
Для построения некоторых сложных
формул массива
может потребоваться
массив
рангов, т.е. тот же набор рангов, но в одной ячейке.
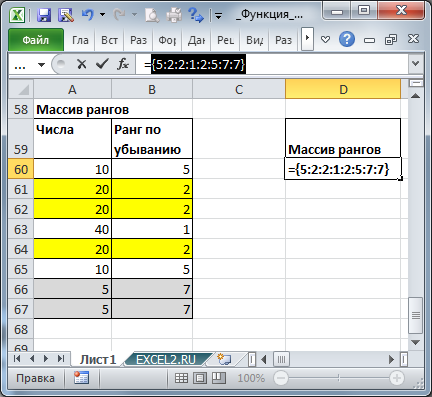
Как видно из картинки выше, значения из диапазона
В60:В67
и в ячейке
D60
совпадают. Такой массив можно получить с помощью формулы
=РАНГ(A60:A67;A60:A67)
или с помощью формулы
=СЧЁТЕСЛИ(A60:A67;”>”&A60:A67)+1
Ранги по возрастанию можно получить с помощью формулы
=РАНГ(A60:A67;A60:A67;1)
или
=СЧЁТЕСЛИ(A60:A67;”<“&A60:A67)+1
.
Такой подход использется в статьях
Отбор уникальных значений с сортировкой в MS EXCEL
и
Динамическая сортировка таблицы в MS EXCEL
.
17 авг. 2022 г.
читать 2 мин
Вы можете использовать следующие формулы для ранжирования значений по группам в Excel:
Формула 1: ранжирование значений по группам
=SUMPRODUCT(( $A$2:$A$13 = A2 )*( $B$2:$B$13 > B2 ))+1
Эта конкретная формула находит ранг значения в ячейке B2 , принадлежащего группе в ячейке A2 .
Эта формула присваивает ранг 1 наибольшему значению, 2 — второму наибольшему значению и т. д.
Формула 2: ранжирование значений по группам (обратный порядок)
=SUMPRODUCT(( $A$2:$A$13 = A2 )*( $B$2:$B$13 < B2 ))+1
Эта конкретная формула находит обратный ранг значения в ячейке B2 , принадлежащего группе в ячейке A2 .
Эта формула присваивает ранг 1 наименьшему значению, 2 — второму наименьшему значению и т. д.
В следующих примерах показано, как использовать каждую формулу в Excel.
Пример 1. Ранжирование значений по группам в Excel
Предположим, у нас есть следующий набор данных в Excel, который показывает очки, набранные баскетболистами в разных командах:
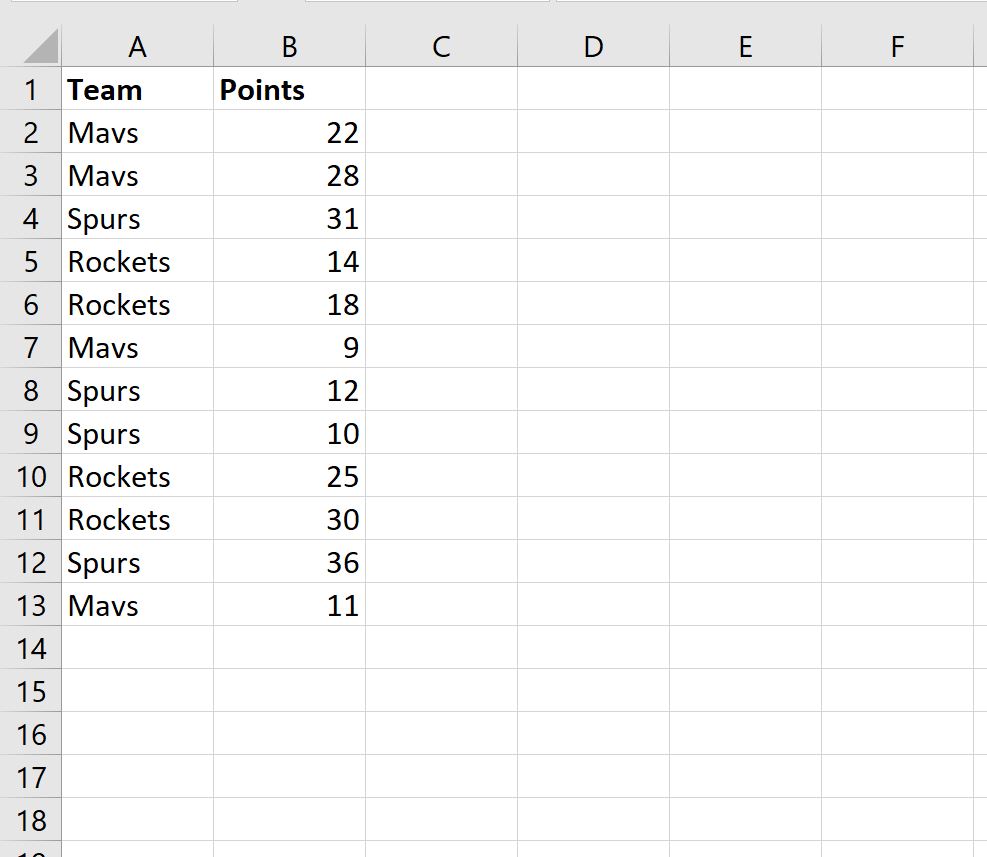
Мы можем использовать следующую формулу для ранжирования очков по командам:
=SUMPRODUCT(( $A$2:$A$13 = A2 )*( $B$2:$B$13 > B2 ))+1
Мы введем эту формулу в ячейку C2 , затем скопируем и вставим формулу в каждую оставшуюся ячейку в столбце C:
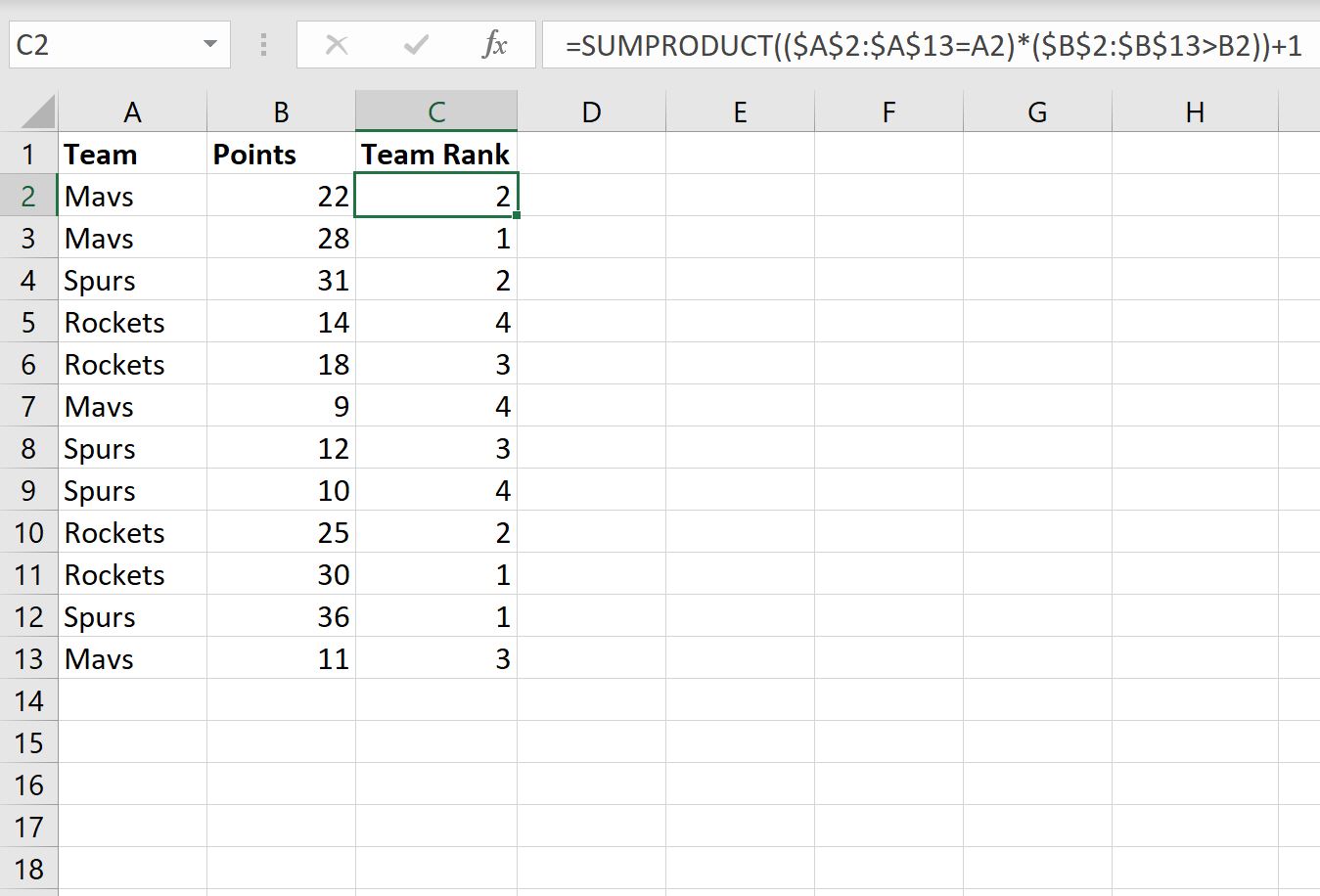
Вот как интерпретировать значения в столбце C:
- Игрок с 22 очками за Mavs занимает второе место по количеству очков среди игроков Mavericks.
- Игрок с 28 очками за Mavs занимает первое место по количеству очков среди игроков Mavericks.
- Игрок с 31 очком за «шпоры» занимает 2-е место по количеству очков среди игроков «шпор».
И так далее.
Пример 2. Ранжирование значений по группам (обратный порядок) в Excel
Еще раз предположим, что у нас есть следующий набор данных в Excel, который показывает очки, набранные баскетболистами в разных командах:

Мы можем использовать следующую формулу для ранжирования очков в обратном порядке по командам:
=SUMPRODUCT(( $A$2:$A$13 = A2 )*( $B$2:$B$13 < B2 ))+1
Мы введем эту формулу в ячейку C2 , затем скопируем и вставим формулу в каждую оставшуюся ячейку в столбце C:
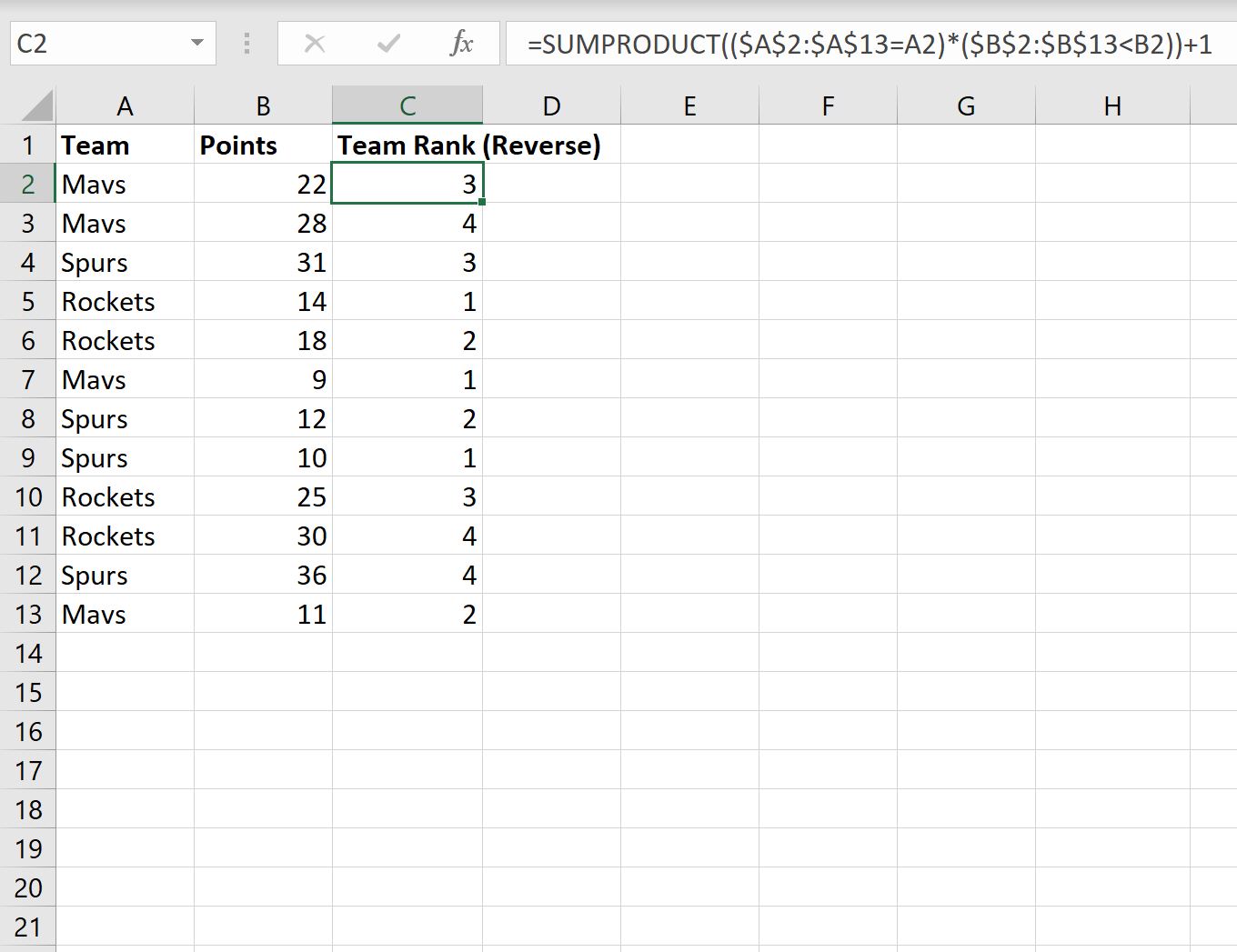
Вот как интерпретировать значения в столбце C:
- Игрок с 22 очками за Mavs занимает 3-е место по наименьшему количеству очков среди игроков Mavericks.
- Игрок с 28 очками за Mavs занимает 4-е место по наименьшему количеству очков среди игроков Mavericks.
- Игрок с 31 очком за «шпоры» занимает 4-е место по наименьшему количеству очков среди игроков «шпор».
И так далее.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как ранжировать элементы по нескольким критериям в Excel
Как сортировать по нескольким столбцам в Excel






