Как найти ранг матрицы ступенчатым способом

Перед тем как начать знакомство с темой, необходимо повторить правила нахождения определителей второго, третьего и высших порядков. Также необходимо знать, что детерминант 1-го порядка — число. Рассмотрим 2 метода вычисления ранга матриц.

Онлайн-калькулятор

Метод окаймляющих миноров

Для нахождения ранга матрицы данным методом требуется уметь находить миноры матриц.

Ранг матрицы

Рангом матрицы QQ называется наивысший порядок миноров, среди которых есть хотя бы один отличный от 00.

При этом ранг матрицы не может превышать порядка матрицы: 0⩽rang Qm×n⩽min(m,n)0leqslant rang Q_{mtimes n}leqslant min (m, n).

Обозначить ранг матрицы QQ можно следующим образом: rang Qrang Q или r(Q)r(Q).

Если ранг матрицы QQ равен rr, то это означает, что в матрице QQ имеется отличный от нуля минор порядка rr. При этом всякий минор порядка больше, чем rr равен нулю.

Исходя из определения ранга матрицы, следует, что если все миноры первого порядка (т. е. элементы матрицы QQ) равны 00, то rang Q=0rang Q=0. Если один из миноров первого порядка отличен от 00, а все миноры второго порядка равны 00, то rang Q=1rang Q=1. Если все миноры kk-го порядка равны 00, или миноров kk-го порядка не существует, то rang Q=k−1rang Q=k-1.

Рассмотрим примеры нахождения ранга матриц данным методом.

Пример 1

Найти ранг матрицы методом окаймляющих миноров

F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.

Данная матрица имеет размер 3×33times3, поэтому ее ранг не может быть больше 33, т.е. rang F⩽3rang Fleqslant3.

Перейдем к вычислению ранга матрицы.

Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang F≥1rang Fgeq1.

Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣0321∣=0⋅1−2⋅3=0−6=−6begin{vmatrix}0&3\2&1end{vmatrix}=0cdot1-2cdot3=0-6=-6. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang F≥2rang Fgeq2.

Перейдем к проверке миноров 3-го порядка. Минор 3-го порядка — определитель матрицы FF, поскольку она состоит из 3 строк и 3 столбцов: ∣03−1210−2−10∣=0begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0. Значит, ранг матрицы FF равен 22, или rang F=2rang F=2.

Пример 2

Найти ранг матрицы методом окаймляющих миноров

K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.

Данная матрица имеет размер 5×45times4. Из чисел 55 и 44 минимальным является 44, поэтому ее ранг не может быть больше 44, а значит rang K⩽4rang Kleqslant4.

Перейдем к вычислению ранга матрицы.

Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang K≥1rang Kgeq1.

Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣21−12∣=2⋅2−(−1)⋅1=4+1=5begin{vmatrix}2&1\-1&2end{vmatrix}=2cdot2-(-1)cdot1=4+1=5. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥2rang Kgeq2.

Перейдем к проверке миноров 3-го порядка. Например, на пересечении строк №1, №3 и №5 и столбцов №2, №3 и №4 получим минор:

∣1−233−153−31∣=1⋅(−1)⋅1+(−2)⋅5⋅3+3⋅(−3)⋅3−3⋅(−1)⋅3−(−2)⋅1⋅3−1⋅5⋅(−3)=−1−30−27+9+6+15=−28begin{vmatrix}1&-2&3\3&-1&5\3&-3&1end{vmatrix}=1cdot(-1)cdot1+(-2)cdot5cdot3+3cdot(-3)cdot3-3cdot(-1)cdot3-(-2)cdot1cdot3-1cdot5cdot(-3)=-1-30-27+9+6+15=-28.

Значит, среди миноров 3-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥3rang Kgeq3.

Перейдем к проверке миноров 4-го порядка. Например, на пересечении строк №1, №2, №3 и №4 и столбцов №1, №2, №3 и №4 получим минор:

∣21−23−121213−15−2−212∣=2(−1)1+1∣2123−15−212∣−(−1)2+1∣1−233−15−212∣+(−1)3+1∣1−23212−212∣−2(−1)4+1∣1−232123−15∣=2(−1)2∣2123−15−212∣−(−1)3∣1−233−15−212∣+(−1)4∣1−23212−212∣−2(−1)5∣1−232123−15∣=2∣2123−15−212∣+∣1−233−15−212∣+∣1−23212−212∣+2∣1−232123−15∣=2(−4+6−10−4−10−6)−2+9+20−6−5+12+2+6+8+6−2+8+2(5−6−12−9+2+20)=−56+56+0=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2end{vmatrix}=2(-1)^{1+1}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{2+1}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{3+1}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{4+1}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-1)^{2}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{3}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{4}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{5}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}+2begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-4+6-10-4-10-6)-2+9+20-6-5+12+2+6+8+6-2+8+2(5-6-12-9+2+20)=-56+56+0=0.

Остальные миноры 4-го порядка также равны нулю:
∣21−23−121213−1543−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}=0,

∣21−23−1212−2−21243−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,

∣21−2313−15−2−21243−31∣=0begin{vmatrix}2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,

∣−121213−15−2−21243−31∣=0begin{vmatrix}-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0.

Значит, ранг матрицы KK равен 33, или rang K=3rang K=3.

Данный метод не всегда удобен, поскольку связан с вычислением большого количества определителей. Рассмотрим метод нахождения ранга матриц, который наиболее часто применяется на практике.

Метод Гаусса (метод элементарных преобразований)

Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:

1. перестановка местами любых двух рядов (строк или столбцов) матрицы;
2. умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
3. прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.

Ранг матрицы

Рангом матрицы называется количество ненулевых строк матрицы после ее приведения к ступенчатому виду при помощи элементарных преобразований над строками и столбцами.

Рассмотрим суть данного метода на примерах.

Пример 1

Найти ранг матрицы методом Гаусса F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.

Приведем матрицу FF с помощью элементарных преобразований к ступенчатому виду.

Поменяем местами строки №1 и №2:

(03−1210−2−10)∼(21003−1−2−10)begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}sim begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}.

Прибавим к строке №3 строку №1, умноженную на 1:

(21003−1−2−10)∼(21003−1000)begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}simbegin{pmatrix}2&1&0\0&3&-1\0&0&0end{pmatrix}.

С помощью элементарных преобразований мы привели матрицу FF к ступенчатому виду. В ней остались 2 ненулевые строки, следовательно, rang F=2rang F=2.

Пример 2

Найти ранг матрицы методом Гаусса

K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.

Приведем матрицу KK с помощью элементарных преобразований к ступенчатому виду.

Поменяем местами строки №1 и №2:

(21−23−121213−15−2−21243−31)∼(−121221−2313−15−2−21243−31)begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.

Поменяем местами строки №2 и №4:

(−121221−2313−15−2−21243−31)∼(−1212−2−21213−1521−2343−31)begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}.

Поменяем местами строки №3 и №4:

(−1212−2−21213−1521−2343−31)∼(−1212−2−21221−2313−1543−31)begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}.

Поменяем местами строки №4 и №5:

(−1212−2−21221−2313−1543−31)∼(−1212−2−21221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.

Прибавим к строке №2 строку №1, умноженную на -2:

(−1212−2−21221−2343−3113−15)∼(−12120−6−1−221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.

Прибавим к строке №3 строку №1, умноженную на 2:

(−12120−6−1−221−2343−3113−15)∼(−12120−6−1−2050743−3113−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}.

Прибавим к строке №4 строку №1, умноженную на 4:

(−12120−6−1−2050743−3113−15)∼(−12120−6−1−205070111913−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}.

Прибавим к строке №5 строку №1, умноженную на 1:

(−12120−6−1−205070111913−15)∼(−12120−6−1−20507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.

Прибавим к строке №2 строку №3, умноженную на 1:

(−12120−6−1−20507011190507)∼(−12120−1−150507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.

Прибавим к строке №5 строку №3, умноженную на -1:

(−12120−1−150507011190507)∼(−12120−1−150507011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}.

Прибавим к строке №3 строку №2, умноженную на 5:

(−12120−1−150507011190000)∼(−12120−1−1500−532011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}.

Прибавим к строке №4 строку №2, умноженную на 11:

(−12120−1−1500−532011190000)∼(−12120−1−1500−53200−10640000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}.

Прибавим к строке №4 строку №3, умноженную на -2:

(−12120−1−1500−53200−10640000)∼(−12120−1−1500−53200000000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&0&0\0&0&0&0end{pmatrix}.

С помощью элементарных преобразований мы привели матрицу KK к ступенчатому виду. В ней остались 3 ненулевые строки, следовательно, rang K=3rang K=3.

Любым из рассмотренных методов можно найти ранг матрицы.

Наши эксперты готовы оказать вам помощь с решением задачи онлайн по самым низким ценам!

Тест по теме «Ранг матрицы»

Уважаемые студенты,

каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконке

Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.

Ранг матрицы. Элементарные преобразования строк матрицы.

Рассмотрим матрицу

.

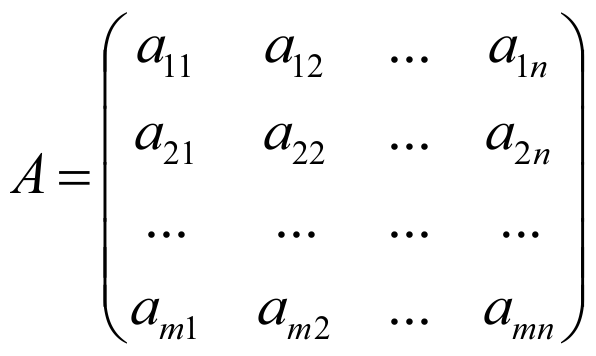Выделим в ней k-строк и k-столбцов (k≤(min(m,n))). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы.

Рассмотрим всевозможные миноры матрицы А, отличные от нуля.

Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля.

Если все элементы матрицы равны нулю, то ранг этой матрицы принимают равным нулю.

Минор, порядок которого определяет ранг матрицы, называется базисным.

У матрицы может быть несколько базисных миноров.

Ранг матрицы А обозначается r(A) . Если r(A)=r(B) , то матрицы А и В называются эквивалентными. Пишут A̴∼В.

Свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевую строку (столбец), то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

Под элементарными преобразованиями понимают:

• Перестановку строк матрицы;
• Умножение какой-либо строки на число, отличное от нуля;
• Прибавление к элементам одной строки соответствующих элементов другой строки, умноженной на произвольное число.

При вычислении ранга матрицы могут быть использованы элементарные преобразования, метод приведения матрицы к ступенчатому виду, метод окаймляющих миноров.

Метод приведения матрицы к ступенчатому виду заключается в том, что при помощи элементарных преобразований данная матрица приводится к ступенчатой.

Матрица называется ступенчатой, если в каждой ее строке первый ненулевой элемент стоит правее, чем в предыдущей (т. е. получаются ступеньки, высота каждой ступеньки должна быть равна единице).

Примеры ступенчатых матриц:

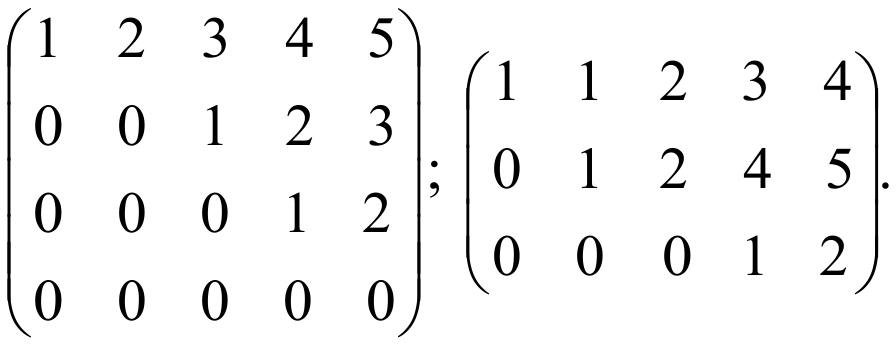
Примеры не ступенчатых матриц:

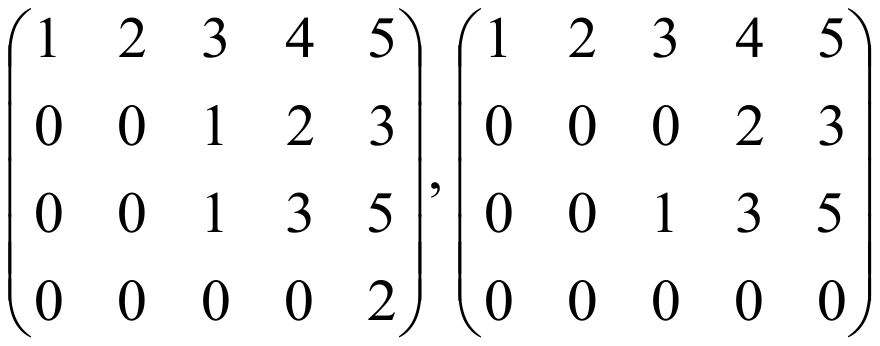
ПРИМЕР: Найти ранг матрицы:

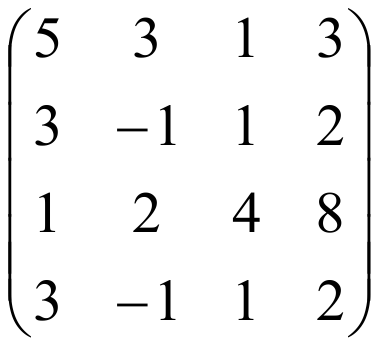
РЕШЕНИЕ:

Приведем данную матрицу к ступенчатой с помощью элементарных преобразований.

1.Поменяем местами первую и третью строки.

2. Получим в первом столбце нули под единицей.

Прибавив ко второй строке первую, умноженную на (-3), к третьей – первую, умноженную на (-5), к четвертой – первую, умноженную на (-3), получим

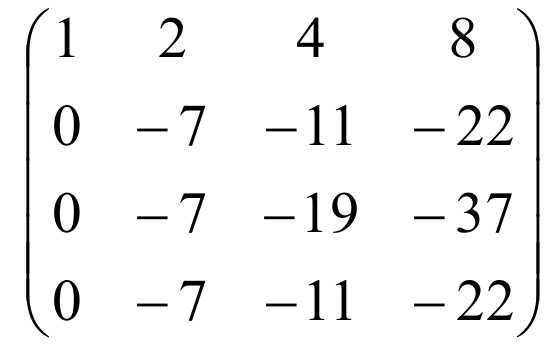
Для того чтобы было понятней где еще нужно получить нули, нарисуем ступеньки в матрице. (Матрица будет ступенчатой, если везде под ступеньками будут нули)

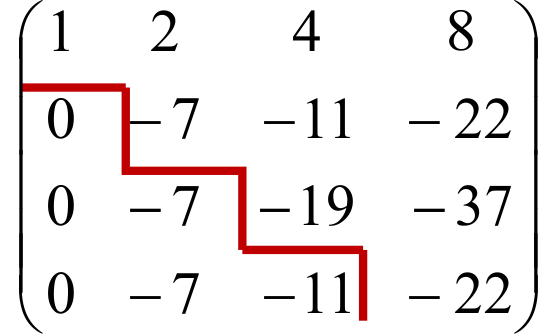
3. Прибавив к третьей строке вторую, умноженную на (-1), к четвертой – вторую, умноженную на (-1), получим нули под ступеньками во втором столбце.

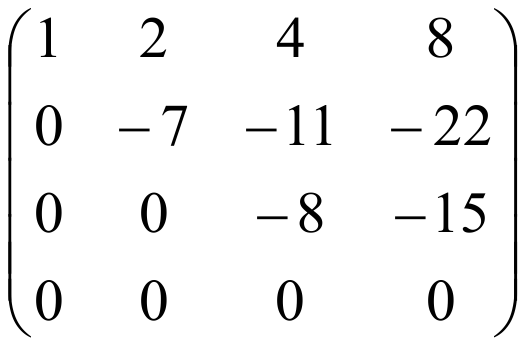
Если нарисовать опять ступеньки, увидим, что матрица ступенчатая.

Ее ранг равен r=3 (число строк ступенчатой матрицы, в каждой из которых хотя бы один элемент отличен от нуля). Следовательно, ранг данной матрицы r=3.

Решение можно записать так:

(римскими цифрами обозначены номера строк)

Ответ: r=3.

Минор порядка k+1, содержащий в себе минор порядка k называется окаймляющим минор.

Метод окаймляющих миноров основан на том, что ранг данной матрицы равен порядку такого минора этой матрицы, который отличен от нуля, а все окаймляющие его миноры равны нулю.

ПРИМЕР : Найти ранг матрицы:

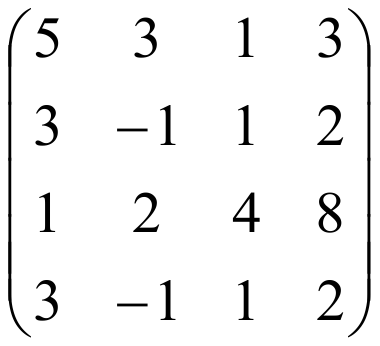
РЕШЕНИЕ:

Найдем теперь ранг этой матрицы методом окаймляющих миноров.

Среди миноров первого порядка есть отличные от нуля, например 5. Среди окаймляющих его миноров есть отличный от нуля, например

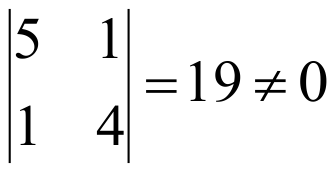
Среди миноров, окаймляющих этот минор, есть отличный от нуля, например

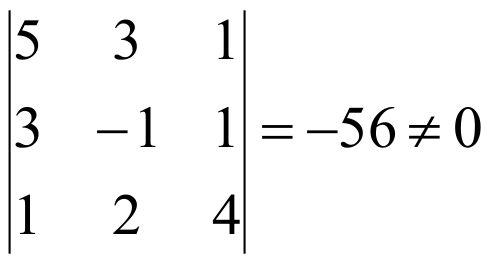
Так как единственный минор, окаймляющий последний минор равен нулю, то r=3.

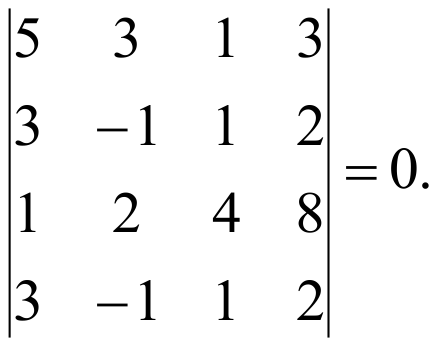
Ответ: r=3.

Упражнения к уроку:

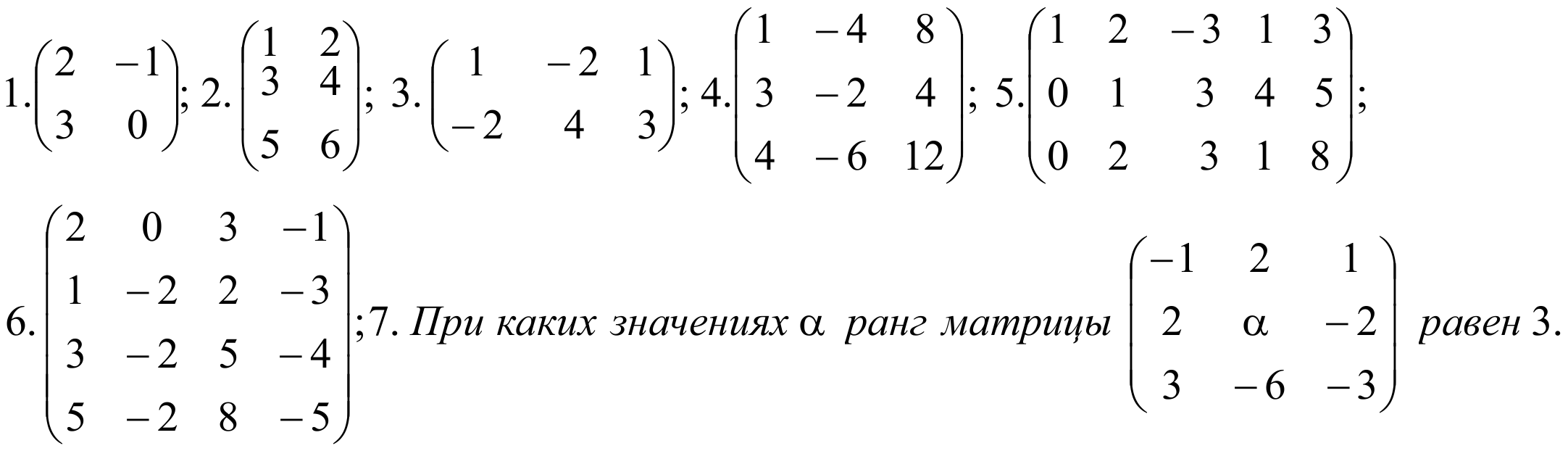
Показать ответ

Вычисление ранга матрицы методом элементарных преобразований (алгоритм Гаусса).

Под элементарными преобразованиями строк (столбцов) матрицы понимают следующие действия:

1. Перемена мест двух строк (столбцов).
2. Умножение всех элементов строки (столбца) на некоторое число $aneq 0$.
3. Суммирование всех элементов одной строки (столбца) с соответствующими элементами иной строки (столбца), умноженными на некое действительное число.

Если применить к строкам или столбцам матрицы $A$ некое элементарное преобразование, то получим новую матрицу $B$. В этом случае $rang{A}=rang{B}$, т.е. элементарные преобразования не изменяют ранг матрицы.

Если $rang A=rang B$, то матрицы $A$ и $B$ называются эквивалентными. Тот факт, что матрица $A$ эквивалентна матрице $B$, записывают так: $Asim B$.

Часто используется и такая запись: $Arightarrow B$, которая означает, что матрица $B$ получена из матрицы $A$ применением некоего элементарного преобразования.

При нахождении ранга методом Гаусса работать можно как со строками, так и со столбцами. Удобнее работать со строками, поэтому в примерах на этой странице преобразования выполняются именно над строками матриц.

Отмечу, что транспонирование не изменяет ранг матрицы, т.е. $rang{A}=rang{A^T}$. Этим свойством в некоторых случаях удобно пользоваться (см. пример №3), так как при необходимости строки легко сделать столбцами и наоборот.

Краткое описание алгоритма

Введём несколько терминов. Нулевая строка – строка, все элементы которой равны нулю. Ненулевая строка – строка, хоть один элемент которой отличен от нуля. Ведущим элементом ненулевой строки называется её первый (считая слева направо) отличный от нуля элемент. Например, в строке $(0;0;5;-9;0)$ ведущим будет третий элемент (он равен 5).

Ранг любой нулевой матрицы равен 0, поэтому станем рассматривать матрицы, отличные от нулевых. Конечная цель преобразований матрицы – сделать её ступенчатой. Ранг ступенчатой матрицы равен количеству ненулевых строк.

Рассматриваемый метод нахождения ранга матрицы состоит из нескольких шагов. На первом шаге используется первая строка, на втором шаге – вторая и так далее. Когда под той строкой, которую мы используем на текущем шаге, остаются лишь нулевые строки, или же не остаётся строк вовсе, то алгоритм прекращается, так как полученная матрица будет ступенчатой.

Теперь обратимся к тем преобразованиям над строками, которые выполняются на каждом шаге алгоритма. Пусть под текущей строкой, которую нам нужно использовать на данном шаге, имеются ненулевые строки, причём $k$ – номер ведущего элемента текущей строки, а $k_{min}$ – наименьший из номеров ведущих элементов тех строк, которые лежат ниже текущей строки.

• Если $klt{k_{min}}$, то переходим к следующему шагу алгоритма, т.е. к использованию следующей строки.
• Если $k=k_{min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. Если появляются нулевые строки, то переносим их в низ матрицы. Затем переходим к следующему шагу алгоритма.
• Если $kgt{k_{min}}$, то меняем местами текущую строку с одной из тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. После этого производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. Если таких строк нет, то переходим к следующему шагу алгоритма. Если появляются нулевые строки, то переносим их в низ матрицы.

Как конкретно происходит обнуление ведущих элементов, рассмотрим на практике. Буквами $r$ (от слова “row”) станем обозначать строки: $r_1$ – первая строка, $r_2$ – вторая строка и так далее. Буквами $c$ (от слова “column”) станем обозначать столбцы: $c_1$ – первый столбец, $c_2$ – второй столбец и так далее.

В примерах на данной странице буквой $k$ я стану обозначать номер ведущего элемента текущей строки, а запись $k_{min}$ будет использована для обозначения наименьшего из номеров ведущих элементов строк, лежащих под текущей строкой.

Пример №1

Найти ранг матрицы $A=left(begin{array}{ccccc}
-2 & 3 & 1 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
4 & -11 & -5 & 12 & 18 \
-9 & 6 & 0 & -2 & 21 \
-5 & 5 & 1 & 1 & 1
end{array} right)$.

Решение

Данная матрица не является нулевой, а значит её ранг больше нуля. Перейдём к первому шагу алгоритма.

Первый шаг

На первом шаге мы работаем с первой строкой. В первой строке заданной нам матрицы ведущим является первый элемент, т.е. номер ведущего элемента первой строки $k=1$. Посмотрим на строки, расположенные под первой строкой. Ведущие элементы в этих строках имеют номера 4, 1, 1 и 1. Наименьшим из этих номеров есть $k_{min}=1$. Так как $k=k_{min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. Иными словами, нужно обнулить ведущие элементы третьей, четвёртой и пятой строк.

В принципе, можно приступать к обнулению указанных выше элементов, однако для тех преобразований, которые выполняются для обнуления, удобно, когда ведущим элементом используемой строки является единица. Это не обязательно, но очень упрощает расчёты. У нас ведущим элементом первой строки есть число -2. Чтобы заменить “неудобное” число единицей (или числом (-1)) есть несколько вариантов. Можно, например, умножить первую строку на 2, а затем от первой строки вычесть пятую. А можно просто поменять местами первый и третий столбцы. После перестановки столбцов №1 и №3 получим новую матрицу, эквивалентную заданной матрице $A$:

$$
left(begin{array}{ccccc}
-2 & 3 & 1 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
4 & -11 & -5 & 12 & 18 \
-9 & 6 & 0 & -2 & 21 \
-5 & 5 & 1 & 1 & 1
end{array}right)overset{c_1leftrightarrow{c_3}}{sim}

left(begin{array}{ccccc}
boldred{1} & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
normblue{-5} & -11 & 4 & 12 & 18 \
0 & 6 & -9 & -2 & 21 \
normgreen{1} & 5 & -5 & 1 & 1
end{array}right)
$$

Ведущим элементом первой строки стала единица. Номер ведущего элемента первой строки не поменялся: $k=1$. Номера ведущих элементов строк, расположенных ниже первой, таковы: 4, 1, 2, 1. Наименьший номер $k_{min}=1$. Так как $k=k_{min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. Это значит, что нужно обнулить ведущие элементы третьей и пятой строк. Эти элементы выделены синим и зелёным цветами.

Чтобы обнулить нужные элементы, будем выполнять операции со строками матрицы. Запишу эти операции отдельно:

$$
begin{aligned}
&r_3-frac{normblue{-5}}{boldred{1}}cdot{r_1}=r_3+5r_1;\
&r_5-frac{normgreen{1}}{boldred{1}}cdot{r_1}=r_5-r_1.
end{aligned}
$$

Запись $r_3+5r_1$ означает, что к элементам третьей строки прибавили соответствующие элементы первой строки, умноженные на пять. Результат записывают на место третьей строки в новую матрицу. Если с устным выполнением такой операции возникают сложности, то это действие можно выполнить отдельно:

$$
r_3+5r_1
=(-5;;-11;;4;;12;;18)+5cdot(1;;3;;-2;;0;;-4)=\

=(-5;;-11;;4;;12;;18)+(5;;15;;-10;;0;;-20)
=(0;;4;;-6;;12;;-2).
$$

Действие $r_5-r_1$ выполняется аналогично. В результате преобразований строк получим такую матрицу:

$$
left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
-5 & -11 & 4 & 12 & 18 \
0 & 6 & -9 & -2 & 21 \
1 & 5 & -5 & 1 & 1
end{array}right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3+5r_1 \ phantom{0} \ r_5-r_1 end{array}sim

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
0 & 4 & -6 & 12 & -2 \
0 & 6 & -9 & -2 & 21 \
0 & 2 & -3 & 1 & 5
end{array}right)
$$

На этом первый шаг можно считать законченным. Так как под первой строкой остались ненулевые строки, то нужно продолжать работу. Единственный нюанс: в третьей строке полученной матрицы все элементы делятся нацело на 2. Чтобы уменьшить числа и упростить себе расчёты, умножим элементы третьей строки на $frac{1}{2}$, а затем уже перейдём ко второму шагу:

$$
left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
0 & 4 & -6 & 12 & -2 \
0 & 6 & -9 & -2 & 21 \
0 & 2 & -3 & 1 & 5
end{array}right)
begin{array} {l} phantom{0}\ phantom{0}\ 1/2cdot{r_3} \ phantom{0} \ phantom{0} end{array}sim

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
0 & 2 & -3 & 6 & -1 \
0 & 6 & -9 & -2 & 21 \
0 & 2 & -3 & 1 & 5
end{array}right)
$$

Второй шаг

На втором шаге мы работаем с второй строкой. Во второй строке матрицы ведущим является четвёртый элемент, т.е. номер ведущего элемента второй строки $k=4$. Посмотрим на строки, расположенные под второй строкой. Ведущие элементы в этих строках имеют номера 2, 2 и 2. Наименьшим из этих номеров есть $k_{min}=2$. Так как $kgt{k_{min}}$, то нужно поменять местами текущую вторую строку с одной из тех строк, у которых номер ведущего элемента равен $k_{min}$. Иными словами, надо поменять вторую строку с третьей, четвёртой или пятой. Я выберу пятую строку (это позволит избежать появления дробей), т.е. поменяю местами пятую и вторую строки:

$$
left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
0 & 2 & -3 & 6 & -1 \
0 & 6 & -9 & -2 & 21 \
0 & 2 & -3 & 1 & 5
end{array}right)
overset{r_2leftrightarrow{r_5}}{sim}

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & boldred{2} & -3 & 1 & 5 \
0 & normblue{2} & -3 & 6 & -1 \
0 & normgreen{6} & -9 & -2 & 21 \
0 & 0 & 0 & 5 & -6
end{array}right)
$$

Опять обратимся ко второй строке. Теперь ведущим в ней является второй элемент (он выделен красным цветом), т.е. $k=2$. Наименьшим из номеров ведущих элементов нижележащих строк (т.е. из чисел 2, 2 и 4) будет $k_{min}=2$. Так как $k=k_{min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. Это значит, что нужно обнулить ведущие элементы третьей и четвёртой строк. Эти элементы выделены синим и зелёным цветами.

Отмечу, что на предыдущем шаге ведущим элементом текущей строки с помощью перестановки столбцов была сделана единица. Это было выполнено, чтобы избежать работы с дробями. Здесь тоже можно поставить единицу на место ведущего элемента второй строки: например, поменяв местами второй и четвёртый столбцы. Однако делать это мы не станем, так как дробей и так не возникнет. Действия со строками будут такими:

$$
begin{aligned}
&r_3-frac{normblue{2}}{boldred{2}}cdot{r_2}=r_3-r_2;\
&r_4-frac{normgreen{6}}{boldred{2}}cdot{r_2}=r_4-3r_2.
end{aligned}
$$

Выполняя указанные операции, придём к такой матрице:

$$
left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 2 & -3 & 1 & 5 \
0 & 2 & -3 & 6 & -1 \
0 & 6 & -9 & -2 & 21 \
0 & 0 & 0 & 5 & -6
end{array}right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3-r_2 \ r_4-3r_2 \ phantom{0} end{array}sim

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 2 & -3 & 1 & 5 \
0 & 0 & 0 & 5 & -6 \
0 & 0 & 0 & -5 & 6 \
0 & 0 & 0 & 5 & -6
end{array}right)
$$

Второй шаг закончен. Так как под второй строкой остались ненулевые строки, то переходим к третьему шагу.

Третий шаг

На третьем шаге мы работаем с третьей строкой. В третьей строке матрицы ведущим является четвёртый элемент, т.е. номер ведущего элемента третьей строки $k=4$. Посмотрим на строки, расположенные под третьей строкой. Ведущие элементы в этих строках имеют номера 4 и 4, наименьший из которых $k_{min}=4$. Так как $k=k_{min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. Это значит, что нужно обнулить ведущие элементы четвёртой и пятой строк. Преобразования, которые выполняются с этой целью, полностью аналогичны тем, что осуществлялись ранее:

$$
left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 2 & -3 & 1 & 5 \
0 & 0 & 0 & 5 & -6 \
0 & 0 & 0 & -5 & 6 \
0 & 0 & 0 & 5 & -6
end{array}right)
begin{array} {l} phantom{0}\ phantom{0}\ phantom{0} \ r_4+r_3 \ r_5-r_3 end{array}sim

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 2 & -3 & 1 & 5 \
0 & 0 & 0 & 5 & -6 \
0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0
end{array}right)
$$

Под третьей строкой остались лишь нулевые строки. Это значит, что преобразования закончены. Мы привели матрицу к ступенчатому виду. Так как приведённая матрица содержит три ненулевых строки, то её ранг равен 3. Следовательно, и ранг исходной матрицы равен трём, т.е. $rang A=3$. Полное решение без пояснений таково:

$$
left(begin{array}{ccccc}
-2 & 3 & 1 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
4 & -11 & -5 & 12 & 18 \
-9 & 6 & 0 & -2 & 21 \
-5 & 5 & 1 & 1 & 1
end{array}right)overset{c_1leftrightarrow{c_3}}{sim}

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
-5 & -11 & 4 & 12 & 18 \
0 & 6 & -9 & -2 & 21 \
1 & 5 & -5 & 1 & 1
end{array}right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3+5r_1 \ phantom{0} \ r_5-r_1 end{array}sim
$$

$$
simleft(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
0 & 4 & -6 & 12 & -2 \
0 & 6 & -9 & -2 & 21 \
0 & 2 & -3 & 1 & 5
end{array}right)
begin{array} {l} phantom{0}\ phantom{0}\ 1/2cdot{r_3} \ phantom{0} \ phantom{0} end{array}sim

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 0 & 0 & 5 & -6 \
0 & 2 & -3 & 6 & -1 \
0 & 6 & -9 & -2 & 21 \
0 & 2 & -3 & 1 & 5
end{array}right)
overset{r_2leftrightarrow{r_5}}{sim}

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 2 & -3 & 1 & 5 \
0 & 2 & -3 & 6 & -1 \
0 & 6 & -9 & -2 & 21 \
0 & 0 & 0 & 5 & -6
end{array}right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3-r_2 \ r_4-3r_2 \ phantom{0} end{array}sim
$$

$$
simleft(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 2 & -3 & 1 & 5 \
0 & 0 & 0 & 5 & -6 \
0 & 0 & 0 & -5 & 6 \
0 & 0 & 0 & 5 & -6
end{array}right)
begin{array} {l} phantom{0}\ phantom{0}\ phantom{0} \ r_4+r_3 \ r_5-r_3 end{array}sim

left(begin{array}{ccccc}
1 & 3 & -2 & 0 & -4 \
0 & 2 & -3 & 1 & 5 \
0 & 0 & 0 & 5 & -6 \
0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0
end{array}right)
$$

Ответ: $rang A=3$.

Пример №2

Найти ранг матрицы $A=left(begin{array}{ccccc}
11 & -13 & 61 & 10 & -11\
2 & -2 & 11 & 2 & -2\
-3 & 5 & -17 & -2 & 3\
4 & 0 & 24 & 7 & -8
end{array} right)$.

Решение

Данная матрица не является нулевой, а значит её ранг больше нуля. Перейдём к первому шагу алгоритма.

Первый шаг

На первом шаге мы работаем с первой строкой. В первой строке заданной нам матрицы ведущим является первый элемент, т.е. номер ведущего элемента первой строки $k=1$. Посмотрим на строки, расположенные под первой строкой. Ведущие элементы в этих строках имеют номер 1, т.е. наименьший из номеров ведущих элементов нижележащих строк есть $k_{min}=1$. Так как $k=k_{min}$, то нужно произвести обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. Иными словами, нужно обнулить ведущие элементы второй, третьей и четвёртой строк.

Для удобства расчётов сделаем так, чтобы ведущим элементом первой строки стала единица. В предыдущем примере для этого мы меняли местами столбцы, однако с этой матрицей такое действие не пройдёт – в данной матрице нет элементов, равных единице. Выполним одно вспомогательное действие: $r_1-5r_2$. Тогда ведущий элемент первой строки станет равен 1.

$$
left(begin{array}{ccccc}
11 & -13 & 61 & 10 & -11\
2 & -2 & 11 & 2 & -2\
-3 & 5 & -17 & -2 & 3\
4 & 0 & 24 & 7 & -8
end{array} right)
begin{array} {l} r_1-5r_2\ phantom{0}\ phantom{0} \ phantom{0} end{array}sim

left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
2 & -2 & 11 & 2 & -2\
-3 & 5 & -17 & -2 & 3\
4 & 0 & 24 & 7 & -8
end{array} right)
$$

Ведущим элементом первой строки стала единица. Обнулим ведущие элементы нижележащих строк:

$$
left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
2 & -2 & 11 & 2 & -2\
-3 & 5 & -17 & -2 & 3\
4 & 0 & 24 & 7 & -8
end{array} right)
begin{array} {l} phantom{0}\ r_2-2r_1\ r_3+3r_1 \ r_4-4r_1 end{array}sim

left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
0 & 4 & -1 & 2 & 0\
0 & -4 & 1 & -2 & 0\
0 & 12 & 0 & 7 & -4
end{array} right)
$$

Первый шаг закончен. Так как под первой строкой остались ненулевые строки, то нужно продолжать работу.

Второй шаг

На втором шаге работаем с второй строкой. Во второй строке матрицы ведущим является второй элемент, т.е. номер ведущего элемента второй строки $k=2$. Ведущие элементы в нижележащих строках имеют тот же номер 2, поэтому $k_{min}=2$. Так как $k=k_{min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{min}$. Это значит, что нужно обнулить ведущие элементы третьей и четвёртой строк.

$$
left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
0 & 4 & -1 & 2 & 0\
0 & -4 & 1 & -2 & 0\
0 & 12 & 0 & 7 & -4
end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3+r_2 \ r_4-3r_2 end{array}sim

left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
0 & 4 & -1 & 2 & 0\
0 & 0 & 0 & 0 & 0\
0 & 0 & 3 & 1 & -4
end{array} right)
$$

Появилась нулевая строка. Опустим её в низ матрицы:

$$
left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
0 & 4 & -1 & 2 & 0\
0 & 0 & 0 & 0 & 0\
0 & 0 & 3 & 1 & -4
end{array} right)
overset{r_3leftrightarrow{r_4}}{sim}

left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
0 & 4 & -1 & 2 & 0\
0 & 0 & 3 & 1 & -4\
0 & 0 & 0 & 0 & 0
end{array} right)
$$

Второй шаг закончен. Заметьте, что мы уже получили ступенчатую матрицу. Впрочем, мы можем формально закончить наш алгоритм. Так как под второй строкой остались ненулевые строки, то следует перейти к третьему шагу и работать с третьей строкой, однако под третьей строкой ненулевых строк нет. Следовательно, преобразования завершены.

К слову, полученная нами матрица является трапециевидной. Трапециевидная матрица – это частный случай ступенчатой матрицы.

Так как данная матрица содержит три ненулевых строки, то её ранг равен 3. Следовательно, и ранг исходной матрицы равен трём, т.е. $rang{A}=3$. Полное решение без пояснений таково:

$$
left(begin{array}{ccccc}
11 & -13 & 61 & 10 & -11\
2 & -2 & 11 & 2 & -2\
-3 & 5 & -17 & -2 & 3\
4 & 0 & 24 & 7 & -8
end{array} right)
begin{array} {l} r_1-5r_2\ phantom{0}\ phantom{0} \ phantom{0} end{array}sim

left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
2 & -2 & 11 & 2 & -2\
-3 & 5 & -17 & -2 & 3\
4 & 0 & 24 & 7 & -8
end{array} right)
begin{array} {l} phantom{0}\ r_2-2r_1\ r_3+3r_1 \ r_4-4r_1 end{array}sim
$$

$$
left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
0 & 4 & -1 & 2 & 0\
0 & -4 & 1 & -2 & 0\
0 & 12 & 0 & 7 & -4
end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3+r_2 \ r_4-3r_2 end{array}sim

left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
0 & 4 & -1 & 2 & 0\
0 & 0 & 0 & 0 & 0\
0 & 0 & 3 & 1 & -4
end{array}right)overset{r_3leftrightarrow{r_4}}{sim}

left(begin{array}{ccccc}
1 & -3 & 6 & 0 & -1\
0 & 4 & -1 & 2 & 0\
0 & 0 & 3 & 1 & -4\
0 & 0 & 0 & 0 & 0
end{array} right)
$$

Ответ: $rang A=3$.

Пример №3

Найти ранг матрицы $A=left(begin{array}{ccc}
0 & 2 & -4 \
-1 & -4 & 5 \
3 & 1 & 7 \
0 & 5 & -10 \
2 & 3 & 0
end{array} right)$.

Решение

Иногда в процессе решения удобно транспонировать матрицу. Так как ранг транспонированной матрицы равен рангу исходной матрицы, то такая операция вполне допустима. В этом примере будет рассмотрен как раз такой случай. В ходе преобразований возникнут две одинаковые строки $(0;;1;;-2)$ (первая и четвёртая). В принципе, можно выполнить действие $r_4-r_1$, тогда четвёртая строка обнулится, однако это лишь удлинит решение на одну запись, поэтому выполнять обнуление четвёртой строки не станем.

$$
left(begin{array}{ccc}
0 & 2 & -4 \
-1 & -4 & 5 \
3 & 1 & 7 \
0 & 5 & -10 \
2 & 3 & 0
end{array} right)
begin{array} {l} 1/2cdot{r_1}\ phantom{0}\ phantom{0} \ 1/5cdot{r_4} \phantom{0} end{array}sim

left(begin{array}{ccc}
0 & 1 & -2 \
-1 & -4 & 5 \
3 & 1 & 7 \
0 & 1 & -2 \
2 & 3 & 0
end{array} right)sim
$$

$$
simleft(begin{array}{ccccc}
0&-1&3&0&2\
1&-4&1&1&3\
-2&5&7&-2&0
end{array} right)
overset{r_1leftrightarrow{r_2}}{sim}

left(begin{array}{ccccc}
1&-4&1&1&3\
0&-1&3&0&2\
-2&5&7&-2&0
end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3+2r_1 end{array}sim
$$

$$
left(begin{array}{ccccc}
1&-4&1&1&3\
0&-1&3&0&2\
0&-3&9&0&6
end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3-3r_2 end{array}sim
left(begin{array}{ccccc}
1&-4&1&1&3\
0&-1&3&0&2\
0&0&0&0&0
end{array} right)
$$

Ранг преобразованной матрицы равен 2, поэтому и ранг исходной матрицы $rang{A}=2$. В принципе, можно было найти ранг и без транспонирования матрицы: поменять местами первую строку с второй, третьей или пятой и продолжить обычные преобразования со строками. Метод сведения матрицы к ступенчатому виду допускает вариации процесса решения.

Ответ: $rang A=2$.

Пример №4

Найти ранг матрицы $A=left(begin{array}{cccccc}
0 & -1 & 2 & -4 & 0 & 5 \
0 & 0 &5 &0 &2 &3 \
0 & 0 & 10 & 0& -4&1
end{array} right)$.

Решение

Данная матрица не является нулевой, т.е. её ранг больше нуля. Перейдём к первому шагу алгоритма.

Первый шаг

На первом шаге мы работаем с первой строкой. В первой строке заданной нам матрицы ведущим является второй элемент, т.е. номер ведущего элемента первой строки $k=2$. Рассмотрим строки, расположенные под первой строкой. Ведущие элементы в этих строках имеют номер 3, т.е. наименьший из номеров ведущих элементов нижележащих строк есть $k_{min}=3$. Так как $klt{k_{min}}$, то переходим к следующему шагу алгоритма.

Второй шаг

На втором шаге мы работаем с второй строкой. Во второй строке ведущим является третий элемент, т.е. номер ведущего элемента второй строки $k=3$. Под второй строкой расположена лишь одна третья строка, номер ведущего элемента которой равен 3, поэтому $k_{min}=3$. Так как $k=k_{min}$, то производим обнуление ведущего элемента третьей строки:

$$
left(begin{array}{cccccc}
0 & -1 & 2 & -4 & 0 & 5 \
0 & 0 &5 &0 &2 &3 \
0 & 0 & 10 & 0& -4&1
end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\ r_3-2r_2 end{array}sim

left(begin{array}{cccccc}
0 & -1 & 2 & -4 & 0 & 5 \
0 & 0 &5 &0 &2 &3 \
0 & 0 & 0 & 0& -8&-5
end{array} right)
$$

Получена ступенчатая матрица. Ранг преобразованной матрицы, а следовательно и ранг исходной матрицы, равен 3.

Ответ: $rang A=3$.

Пример №5

Найти ранг матрицы $A=left(begin{array}{ccccc}
0&0&0&0&6\
9&0&0&0&-11\
5&2&0&0&-5.
end{array} right)$.

Решение

Иногда можно свести матрицу к ступенчатой с помощью одних лишь перестановок строк или столбцов. Это бывает, разумеется, крайне редко, однако удачная перестановка позволяет существенно упростить решение.

$$
left(begin{array}{ccccc}
0&0&0&0&6\
9&0&0&0&-11\
5&2&0&0&-5
end{array} right)
overset{r_1leftrightarrow{r_3}}{sim}

left(begin{array}{ccccc}
5&2&0&0&-5\
9&0&0&0&-11\
0&0&0&0&6
end{array} right)
overset{с_1leftrightarrow{с_4}}{sim}

left(begin{array}{ccccc}
0&2&0&5&-5\
0&0&0&9&-11\
0&0&0&0&6
end{array} right)
$$

Матрица приведена к ступенчатой, $rang{A}=3$.

Ответ: $rang A=3$.

Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.

Ранг матрицы

Определение

Ранг матрицы $ A $ – это максимальное количество линейно-независимых строк (столбцов) этой матрицы. Обозначается $ rang A $ или $ r(A) $.

Формула ранга матрицы гласит, что он не должен превышать порядка этой же матрицы: 

$$ 0 leq rang A_{m times n} leq min (m,n) $$

Чтобы найти ранг матрицы существует два метода:

1. Метод окамляющих миноров
2. Метод элементарных преобразований

На практике применяется второй способ, так как он универсальный и позволяет вычислять ранг матриц любого порядка. Основан он на свойстве, заключаещегося в том, что $ rang A $ не меняется в случае проведения элементарных преобразований над матрицей. Путём приведения матрицы к ступенчатому виду мы узнаем количество линейно-независимых строк (столбцов), которое равно рангу матрицы.

Пример 1

Определить ранг матрицы $$ A = begin{pmatrix} 2&0&-2 \ -4&0&4 end{pmatrix} $$

Решение

Пример решаем с помощью элементарных преобразований. Приводим матрицу к ступенчатой форме.  Прибавляем удвоенную первую строку ко второй: $$ A = begin{pmatrix} 2&0&-2 \ -4&0&4 end{pmatrix} overset{c_2+2c_1}{thicksim} begin{pmatrix} 2&0&-2 \ 0&0&0 end{pmatrix} $$ В полученной матрице появилась нулевая строка, которую необходимо убрать из матрицы: $$ begin{pmatrix} 2&0&-2 \ 0&0&0 end{pmatrix} thicksim begin{pmatrix} 2&0&-2 end{pmatrix} $$ Теперь после преобразований количество строк $ m = 1 $, количество столбцов $ n=3 $. Наименьшее число $ m = 1 $, поэтому $ rang A = 1 $. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ rang A = 1 $$

Пример 2

Найти ранг матрицы: $$ A = begin{pmatrix} 4&2&3 \ 5&2&1 \ 9&4&4 end{pmatrix} $$

Решение

Выполняем элементарные преобразования над матрицей, чтобы узнать количество линейно-независимых строк. Вычитаем из второй строки, умноженной на четверку, первую строку, умноженную на пятерку: $$ A = begin{pmatrix} 4&2&3 \ 5&2&1 \ 9&4&4 end{pmatrix} overset{4c_2-5c_1}{thicksim} begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 9&4&4 end{pmatrix} $$ Вычитаем из третьей строки, умноженной на четыре, первую строку, умноженную на девять: $$ begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 9&4&4 end{pmatrix} overset{4c_3-9c_1}{thicksim}begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 0&-2&-11 end{pmatrix} $$ Вычитаем из третьей строки вторую строку: $$ begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 0&-2&-11 end{pmatrix} overset{4c_3-9c_1}{thicksim}begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 0&0&0 end{pmatrix} $$ Замечаем, что последняя строка матрицы нулевая, значит её можно вычеркнуть: $$ begin{pmatrix} 4&2&3 \ 0&-2&-11 \ 0&-2&-11 end{pmatrix} thicksim begin{pmatrix} 4&2&3 \ 0&-2&-11 end{pmatrix} $$ После элементарных преобразований количество строк уменьшилось и стало $ m=2 $, а количество столбцов $ n = 3 $. По формуле ранга матрицы берем минимальные число из $ m $ и $ n $, то есть $ m=2 $. Получили, что $ rang A = 2 $

Ответ

$$ rang A = 2 $$

В данной публикации мы рассмотрим определение ранга матрицы, а также методы, с помощью которых его можно найти. Также разберем примеры для демонстрации применения теории на практике.

Определение ранга матрицы

Ранг матрицы – ранг ее системы строк или столбцов. В любой матрице есть ее строчный и столбцовый ранги, которые равны между собой.

Ранг системы строк – это максимальное количество линейно-независимых строк. Аналогичным образом определяется ранг системы столбцов.

Примечания:

• Ранг нулевой матрицы (обозначается символом “θ“) любого размера равняется нулю.
• Ранг любого ненулевого вектора-строки или вектора-столбца равняется единице.
• Если в матрице любых размеров присутствует хотя бы один элемент, не равный нулю, значит ее ранг не меньше единицы.
• Ранг матрицы не больше её минимальной размерности.
• Элементарные преобразования, выполненные над матрицей, не меняют её ранга.

Нахождение ранга матрицы

Метод окаймляющих миноров

Ранг матрицы равняется максимальному порядку ненулевого минора.

Алгоритм следующий: находим миноры от низших порядков к высоким. Если минор n-го порядка не равняется нулю, а все последующие (n+1) равны 0, значит ранг матрицы равен n.

Пример
Чтобы было понятнее, давайте разберем практический пример и найдем ранг матрицы A ниже, пользуясь методом окаймляющих миноров.

Решение
Мы имеем дело с матрицей 4×4, следовательно, ее ранг не может быть выше 4. Также в матрице присутствуют ненулевые элементы, значит, ее ранг не меньше единицы. Итак, приступим:

1. Начинаем проверять миноры второго порядка. Для начала берем две строки первого и второго столбцов.

Минор равняется нулю.

Следовательно переходим к следующему минору (первый столбец остается, а вместо второго берем третий).

Минор равен 54≠0, следовательно ранг матрицы не меньше двух.

Примечание: Если бы и этот минор оказался равным нулю, мы бы дальше проверили следующие комбинации:

Если требуется, перебор можно аналогичным образом продолжить со строками:

• 1 и 3;
• 1 и 4;
• 2 и 3;
• 2 и 4;
• 3 и 4.

Если бы все миноры второго порядка оказались равными нулю, то ранг матрицы равнялся бы одному.

2. Нам удалось почти сразу найти минор, который нам подходит. Поэтому переходим к минорам третьего порядка.

К найденному минору второго порядка, который дал отличный от нуля результат, добавляем одну строку и один из столбцов, выделенных зеленым цветом (начнем со второго).

Минор оказался равным нулю.

Следовательно меняем второй столбец на четвертый. И со второй попытки нам удается найти минор, не равный нулю, значит ранг матрицы не может быть меньше 3.

Примечание: если бы результат снова оказался равным нулю, вместо второй строки мы бы дальше взяли четвертую и продолжили бы поиски “хорошего” минора.

3. Теперь остается определить миноры четвертого порядка с учетом найденного ранее. В данном случае он один, который совпадает с определителем матрицы.

Минор равняется 144≠0. А это значит, что ранг матрицы A равняется 4.

Приведение матрицы к ступенчатому виду

Ранг ступенчатой матрицы равняется количеству её ненулевых строк. То есть все, что нам нужно сделать – это привести матрицу к соответствующему виду, например, с помощью элементарных преобразований, которые, как мы уже упомянули выше, не меняют ее ранг.

Пример
Найдем ранг матрицы B ниже. Мы не берем слишком сложный пример, т.к. наша основная цель – это просто продемонстрировать применение метода на практике.

Решение
1. Сначала вычтем из второй строки удвоенную первую.

2. Теперь отнимем из третьей строки первую, умноженную на четыре.

Таким образом, мы получили ступенчатую матрицу, в которой количество ненулевых строк равняется двум, следовательно ее ранг, также, равен 2.