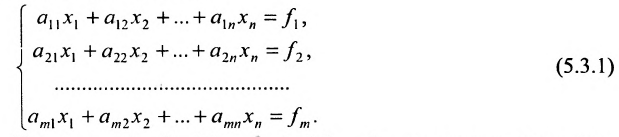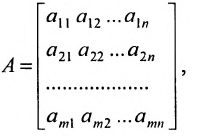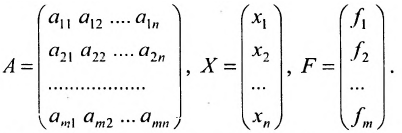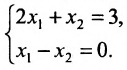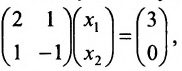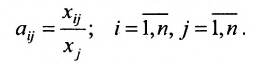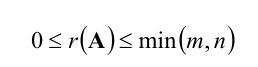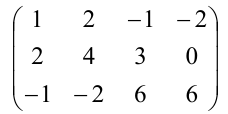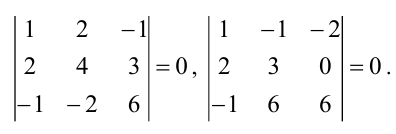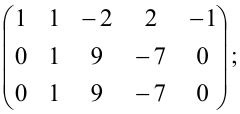Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи”. В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde{A}$.
Теорема Кронекера-Капелли
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde{A}$.
Напомню, что система называется совместной, если она имеет хоть одно решение. Теорема Кронекера-Капелли говорит вот о чём: если $rang A=rangwidetilde{A}$, то решение есть; если $rang Aneqrangwidetilde{A}$, то данная СЛАУ не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы Кронекера-Капелли. В формулировке следствия использована буква $n$, которая равна количеству переменных заданной СЛАУ.
Следствие из теоремы Кронекера-Капелли
- Если $rang Aneqrangwidetilde{A}$, то СЛАУ несовместна (не имеет решений).
- Если $rang A=rangwidetilde{A} < n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Если $rang A=rangwidetilde{A} = n$, то СЛАУ является определённой (имеет ровно одно решение).
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Пример №1
Исследовать СЛАУ $
left {begin{aligned}
& -3x_1+9x_2-7x_3=17;\
& -x_1+2x_2-4x_3=9;\
& 4x_1-2x_2+19x_3=-42.
end{aligned}right.$ на совместность. Если СЛАУ совместна, указать количество решений.
Решение
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde{A}$, запишем их:
$$
A=left( begin{array} {ccc}
-3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19
end{array} right);;
widetilde{A}=left( begin{array} {ccc|c}
-3 & 9 &-7 & 17 \ -1 & 2 & -4 & 9\ 4 & -2 & 19 & -42
end{array} right).
$$
Нужно найти $rang A$ и $rangwidetilde{A}$. Для этого есть много способов, некоторые из которых перечислены в разделе “Ранг матрицы”. Обычно для исследования таких систем применяют два метода: “Вычисление ранга матрицы по определению” или “Вычисление ранга матрицы методом элементарных преобразований”.
Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы “Формулы для вычисления определителей второго и третьего порядков”:
$$
Delta A=left| begin{array} {ccc}
-3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19
end{array} right|=-21.
$$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.
Нам требуется найти также и $rangwidetilde{A}$. Давайте посмотрим на структуру матрицы $widetilde{A}$. До черты в матрице $widetilde{A}$ находятся элементы матрицы $A$, причём мы выяснили, что $Delta Aneq 0$. Следовательно, у матрицы $widetilde{A}$ есть минор третьего порядка, который не равен нулю. Миноров четвёртого порядка матрицы $widetilde{A}$ составить мы не можем, поэтому делаем вывод: $rangwidetilde{A}=3$.
Так как $rang A=rangwidetilde{A}$, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение (хотя бы одно). Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: $x_1$, $x_2$ и $x_3$. Так как количество неизвестных $n=3$, то делаем вывод: $rang A=rangwidetilde{A}=n$, поэтому согласно пункту №3 следствия из теоремы Кронекера-Капелли, система является определённой, т.е. имеет единственное решение.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Способ №2. Вычисление ранга методом элементарных преобразований.
Подробно это метод описан в соответствующей теме. Мы станем вычислять ранг матрицы $widetilde{A}$. Почему именно матрицы $widetilde{A}$, а не $A$? Дело в том, что матрица $A$ является частью матрицы $widetilde{A}$, поэтому вычисляя ранг матрицы $widetilde{A}$ мы одновременно найдем и ранг матрицы $A$.
begin{aligned}
&widetilde{A} =left( begin{array} {ccc|c}
-3 & 9 &-7 & 17 \ -1 & 2 & -4 & 9\ 4 & -2 & 19 & -42
end{array} right) rightarrow left|text{меняем местами первую и вторую строки}right| rightarrow \
&rightarrow left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
-3 & 9 &-7 & 17\
4 & -2 & 19 & -42
end{array} right)
begin{array} {l} phantom{0} \ r_2-3r_1\ r_3+4r_1 end{array} rightarrow
left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
0 & 3 &5 & -10\
0 & 6 & 3 & -6
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\ r_3-2r_2 end{array}rightarrow\
&rightarrow left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
0 & 3 &5 & -10\
0 & 0 & -7 & 14
end{array} right)
end{aligned}
Мы привели матрицу $widetilde{A}$ к ступенчатому виду. Полученная ступенчатая матрица имеет три ненулевых строки, поэтому её ранг равен 3. Следовательно, и ранг матрицы $widetilde{A}$ равен 3, т.е. $rangwidetilde{A}=3$. Делая преобразования с элементами матрицы $widetilde{A}$ мы одновременно преобразовывали и элементы матрицы $A$, расположенные до черты. Матрица $A$ также приведена к ступенчатому виду: $left( begin{array} {ccc}
-1 & 2 & -4 \
0 & 3 &5 \
0 & 0 & -7
end{array} right)$. Вывод: ранг матрицы $A$ также равен 3, т.е. $rang A=3$.
Так как $rang A=rangwidetilde{A}$, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение. Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: $x_1$, $x_2$ и $x_3$. Так как количество неизвестных $n=3$, то делаем вывод: $rang A=rangwidetilde{A}=n$, поэтому согласно пункту №3 следствия из теоремы Кронекера-Капелли, система определена, т.е. имеет единственное решение.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
Пример №2
Исследовать СЛАУ
$ left{ begin{aligned}
& x_1-x_2+2x_3=-1;\
& -x_1+2x_2-3x_3=3;\
& 2x_1-x_2+3x_3=2;\
& 3x_1-2x_2+5x_3=1;\
& 2x_1-3x_2+5x_3=-4.
end{aligned} right.$
на совместность.
Решение
Находить ранги матрицы системы и расширенной матрицы системы будем методом элементарных преобразований. Расширенная матрица системы: $widetilde{A}=left( begin{array} {ccc|c} 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -1 & 3 & 2 \ 3 & -2 & 5 & 1 \ 2 & -3 & 5 & -4 end{array} right)$. Найдём требуемые ранги, преобразовывая расширенную матрицу системы:
$$
left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
-1 & 2 & -3 & 3 \
2 & -3 & 5 & -4 \
3 & -2 & 5 & 1 \
2 & -1 & 3 & 2 end{array} right)
begin{array} {l} phantom{0}\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1end{array}rightarrow
left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & -1 & 1 & -2 \
0 & 1 & -1 & 4 \
0 & 1 & -1 & 4 end{array} right)
begin{array} {l} phantom{0}\phantom{0}\r_3-r_2\ r_4-r_2\r_5+r_2end{array}rightarrow\
$$
$$
rightarrowleft( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 0 end{array} right)
begin{array} {l} phantom{0}\phantom{0}\phantom{0}\ r_4-r_3\phantom{0}end{array}rightarrow
left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 end{array} right)
$$
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde{A}=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang{A}=2$.
Так как $rang Aneqrangwidetilde{A}$, то согласно теореме Кронекера-Капелли система несовместна (т.е. не имеет решений).
Ответ: система несовместна.
Пример №3
Исследовать СЛАУ
$$left{ begin{aligned}
& 2x_1+7x_3-5x_4+11x_5=42;\
& x_1-2x_2+3x_3+2x_5=17;\
& -3x_1+9x_2-11x_3-7x_5=-64;\
& -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\
& 7x_1-17x_2+23x_3+15x_5=132.
end{aligned} right.$$
на совместность.
Решение
Приводим расширенную матрицу системы к ступенчатому виду:
$$
left( begin{array}{ccccc|c}
2 & 0 & 7 & -5 & 11 & 42\
1 & -2 & 3 & 0 & 2 & 17 \
-3 & 9 & -11 & 0 & -7 & -64 \
-5 & 17 & -16 & -5 & -4 & -90 \
7 & -17 & 23 & 0 & 15 & 132 end{array} right)
overset{r_1leftrightarrow{r_3}}{rightarrow}
$$
$$
rightarrowleft( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
2 & 0 & 7 & -5 & 11 & 42\
-3 & 9 & -11 & 0 & -7 & -64\
-5 & 17 & -16 & -5 & -4 & -90 \
7 & -17 & 23 & 0 & 15 & 132 end{array} right)
begin{array} {l} phantom{0}\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end{array} rightarrow
left( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 3 & -2 & 0 & -1 & -13\
0 & 7 & -1 & -5 & 6 & -5 \
0 & -3 & 2 & 0 & 1 & 13 end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end{array} rightarrow
$$
$$
rightarrowleft( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 0 & -11 & 15 & -25 & -76\
0 & 0 & -11 & 15 & -25 & -76 \
0 & 0 & 11 & -15 & 25 & 76 end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\phantom{0} \ r_4-r_3 \ r_5+r_2 end{array} rightarrow
left( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 0 & -11 & 15 & -25 & -76\
0 & 0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0 & 0 end{array} right)
$$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde{A}=rang{A}lt{n}$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Ранг матрицы и системы линейных алгебраических уравнений
Пусть рассматривается система m
линейных алгебраических уравнений
с n неизвестными
( 16 )
Введем в рассмотрение две матрицы
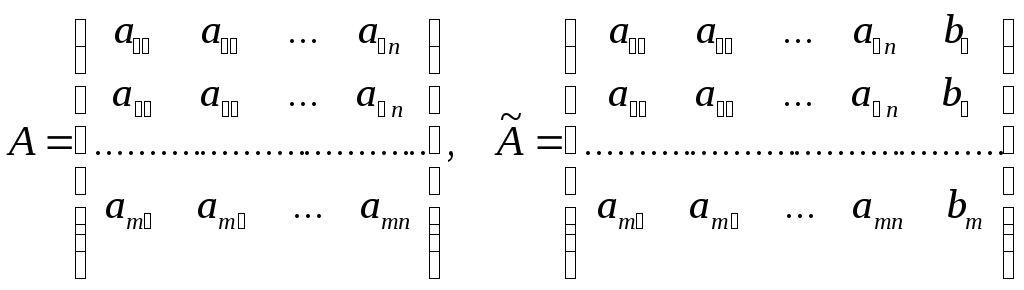
( 17 )
Первая образована коэффициентами при
неизвестных и называется матрицей
системы. Вторая отличается от первой
дополнительным столбцом свободных
членов и называется расширенной
матрицей.
Очевидно,
,
( 18 )
то есть ранг матрицы системы A
не может быть больше ранга расширенной
ма-трицы
.
Теорема (Кронекера4-Капелли5).
Система линейных алгебраических
ура-внений (16) совместна тогда и только
тогда, если ранг матрицы системы A
равен рангу расширенной матрицы
,
.
( 19 )
Теорема Кронекера – Капелли определяет
следующий план исследования системы
уравнений (16).
-
Находим ранги матрицы системы A
и расширенной матрицы
.
Если
,
система несовместна.
-
Рассмотрим теперь основной случай,
когда
,
где k – некоторое
число. Очевидно,
,
то есть k не
превосходит ни чи-сла уравнений, ни
числа неизвестных.
На основании определения ранга матрицы
матрица А содержит по крайней мере
один отличный от нуля минор
k-го порядка, а все
миноры высших порядков обеих матриц А
и
равны нулю. Такой минор называется
базисным. Строки, в которых он
находится, определяют k
базисных уравнений данной системы
уравнений. Столбцы, в которых он находится,
определяют k базисных
неизвестных системы.
Пусть, для определенности, базисный
минор
расположен на пересечении первых k
строк и столбцов матрицы системы А,
то есть
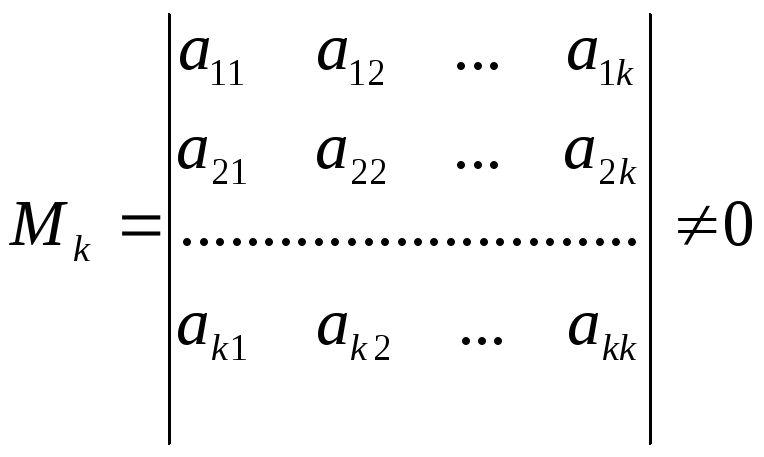
В этом случае базисными уравнениями и
неизвестными являются первые k
ура-внений и первые k
неизвестных.
Если количество m
уравнений системы (16) превышает число
k, мы можем оставить
только k базисных
уравнений, а остальные
уравнений отбросить, так как они, на
основании соответствующей теории,
которую мы во втузе не изучаем, являются
следствиями базисных уравнений. Таким
образом, мы должны рассматривать далее
систему только k
первых уравнений системы (16) с n
неизвестными. Могут представиться
два случая.
А) Количество неизвестных n
равно k (),
то есть все неизвестные являются
базисными, и мы имеем систему k
уравнений с k
неизвестными и отличным от нуля
главным определителем
.
Такая система является сов-местной,
имеющей единственное решение, которое
мы можем найти одним из трех рассмотренных
выше методов (правило Крамера, метод
Гаусса или Жордана – Гаусса, матричный
метод).
Б) Количество неизвестных n
превышает k ().
В этом случае k базисных
неизвестных мы оставляем слева, а
остальные
неизвестных (так называемых свободных
неизвестных) переносим направо, считая
их произвольными. После этого мы решает
полученную систему уравнений относительно
базисных неизвестных (одним из только
что названных методов), то есть фактически
выражаем базисные неизвестные через
свободные. Система (16) является в этом
случае совместной, имеющей бесконечное
множество решений (так как свободные
неизвестные могут принимать какие
угодно значения), и мы получаем так
называемое общее решение системы.
Пример. Исследовать на совместность и
решить систему линейных алгебраических
уравнений
-
Матрица системы и расширенная матрица
имеют один и тот же ранг
.
Ранг первой матрицы мы нашли выше, ранг
второй найдите самостоятельно.
Следовательно, данная система уравнений
совместна.
2. Выберем в качестве базисного минора
(второго порядка) минор, расположенный
на пересечении первых двух строк и
столбцов матрицы системы А,
.
Такой выбор базисного минора определяет
первые два уравнения и неизвестные как
базисные.
Количество уравнений ()
превышает число
,
поэтому мы оставляем только базисные
уравнения данной системы, то есть сводим
ее к виду
Количество неизвестных ()
превышает число
,
поэтому мы оставляем слева только
базисные неизвестные
,
перенося направо свободные неизвестные
,
Полученную систему уравнений мы решаем
относительно
методом Гаусса. Именно, прибавляя к
первому уравнению второе, предварительно
умно-женное на -3, получаем
откуда
.
Ответ: общее решение данной системы
уравнений имеет вид
,
где
– произвольные числа.
Замечание. Можно положить
и представить общее решение в несколько
иной форме, именно
,
где–
произвольные числа.
Подчеркнем, что базисных миноров может
быть несколько, и каждый из них определяет
свои наборы базисных уравнений и
неизвестных. Выбор базисного минора
осуществляется самим студентом, решающим
систему уравнений.
Пример. Исследовать на совместность
уже рассматривавшуюся выше си-стему
уравнений
Матрица системы и расширенная матрица
здесь
Матрица А имеет отличный от нуля
минор второго порядка
.
Ее единственный минор третьего порядка
(он же – и главный определитель данной
системы уравнений)
Если
,
то
,
следовательно
,
и система имеет единственное решение,
то есть она является совместной
определенной.
При
обе матрицы принимают вид
ранг матрицы А равен 2, и нужно
исследовать расширенную матрицу на ее
ранг. Воспользуемся элементарными
преобразованиями
Вот три первых из этих преобразований:
а) третий столбец, умноженный на 3, 4 и
-3, прибавляется соответственно к первому,
второму и четвертому столбцам; б) первый
столбец делится на 14, а второй – на 15;
в) вторая строка, умноженная на -1,
прибавляется к третьей. Далее подумайте
самостоятельно.
Для последней из полученных выше матриц
(неизменного ранга!) рассматриваем
миноры второго и третьего порядков, а
именно:
Таким образом, если
,
то
,
и система несовместна. Она является
совместной (и неопределенной) для
,
так как в этом случае
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Система x+y+z=12x+2y+2z=3не имеет решений, поэтому она несовместна.
Система x+y=12x+7y=-3имеет единственное решение x=2; y=1.
Система x+y=12x+2y=23x+3y=3имеет бесконечное множество решений x=ty=1-tпри -∞<t<∞.
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m=n, то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r(A), rg(A), rA.
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k не равно нулю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r(А)≤min (m; n) ;
- когда все элементы матрицы равны нулю, то только тогда r(A)=0 .
А1=111222333, B1=100000
r(A1)=1, r(B1)=1
А2=123405670000; В2=11312143125054136
r(A2)=2; r(B2)=2
А3=111123149
r(A3)=3
Ранг матрицы А1 вычислен на основании свойства определителя, который содержит строки с пропорциональными элементами, поскольку любой минор второго или третьего порядка матрицы А1 равняется нулю.
Ранги матриц В1, А2 вычислены при помощи вычеркивания нулевых строк, поскольку в матрице А2 минор отличается от нуля на пересечении 2-х первых строк и 2-х первых столбцов.
Матрица А3 — невырожденная, поскольку ее ранг равняется 3. (Можно проверить условие ∆=А3 не равно нулю).
Теперь вычислим ранг матрицы В2 при помощи элементарных преобразований:
- элементы 1-ой строки умножим на (-2) и прибавим к соответствующим элементам 2-ой строки;
- элементы 1-ой строки умножим на (-1) и прибавим к соответствующим элементам 3-ей строки;
- элементы 1-ой строки умножим на (-5) и прибавим к соответствующим элементам 4-ой строки:
В2=11312143125054136 (-2)(-1)(-5)+++⇒11310-1-21012-10-1-21⇒
3-ю строку прибавим ко 2-ой и 4-ой строкам:
⇒11310000012-10000⇒1131012-1
Таким образом, число ненулевых строк равно 2 или минор 2-го порядка в левом углу матрицы:
М(2)=1101=10 не равно нулю⇒r(B2)=2
ч.т.д.
Теорема Кронеккера-Капелли (о разрешимости СЛАУ)
Теорема Кронеккера-Капелли — теорема, которая доказывает: чтобы СЛАУ была совместной, необходимым и достаточным условием является равенство ранга r матрицы рангу расширенной матрицы.
Для совместных СЛАУ справедливой считается следующая теорема.
Пусть ранг матрицы, которая составлена из коэффициентов СЛАУ, равен рангу расширенной матрицы. В таком случае, если r=n (где n — число неизвестных системы), то система имеет единственное решение, если r<n, то система имеет бесконечное множество решений.
Если система определена, то для ее решения подходят методы Крамера, Гаусса и матричный метод.
Если система не определена, то некоторым (n-r) неизвестным (свободным) можно давать произвольные значения, а r неизвестных (базисных) определяются через свободные единственным способом.
При этом базисными становятся те, чей определитель, который составлен из коэффициентов при них и отличен от нуля. Выражения главных переменных, которые получены через свободные, объявляются решением системы.
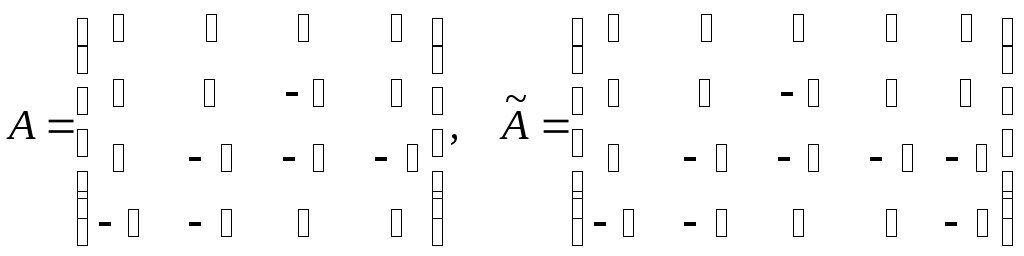
Исследуем и решаем матрицу:
x -2x -x + 2x =12x – x + 4x +4x =5 +4x -2x +x =54x +x +4x +9x =2
Составляем расширенную матрицу системы и приводим ее к ступенчатому виду методом Гаусса.
Определяем ее ранг, а ранг основной матрицы определяем закрытием столбца правых частей.
1-2-1212-144504-21541492(-2)(-4)++⇒1-2-1210360304-2150981-2÷(3)⇒
⇒1-2-121012010-2-2150881-2(-4)(-9)++1-2-1210120100-101100-101-11(-1)+⇒
⇒0-2-1210120100-10110000-12⇒r(A)=31(Ap)=41r(A) не равно r(Ap).
Ответ: система не совместна.
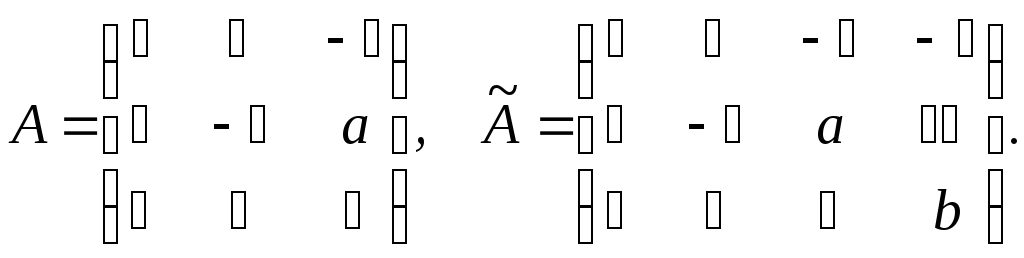
Рассматриваем систему линейных уравнений и находим ранг матрицы:
n=4, m=3:x1-3×2+4×3-x4=13×1+7×2-10×3+5×4=52×1+2x-3x32x4=3
A=1-34-137-10522-32(-3)(-2)++⇒1-34-1016-22808-11412+⇒
⇒1-34-1016-2280000⇒r(A)=2
Составляем расширенную матрицу системы и находим ее ранг:
Ap=1-34-137-10522-32153(-3)(-2)++⇒1-34-1016-22808-11412112+⇒
⇒1-34-1016-2280000120⇒r(Ap)=2
r(A)=r(Ap)=2 — система совместная, r=2<n=4 ⇒ — система неопределенная.
Решаем систему методом Гаусса: преобразования расширенной матрицы системы приводят к системе уравнений вида:
x1-3×2+4×3-x4=116×2-22×3+8×4=2; ∆=1-3016=16 не равно нулю.
Главные переменные — x1 и x2. Свободные переменные — неизвестные x3 и x4. Записываем систему уравнений в виде:
x1-3×2=1-4×3+x48x2=1+11×3-4×4
С помощью обратного хода находим:
x=118x-12x+18.
Из 1-го уравнения:
x1=3×2-4×3+x4+1=338×3-32×4+38-4×3+x4+1=18×3-12×4+118
Ответ: система неопределенная.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец – как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: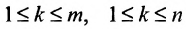
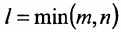
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 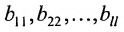
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка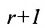
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 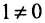
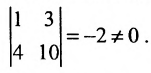
Значит ранг матрицы равен 2.
Пример:
Найти ранг матрицы:
Решение:
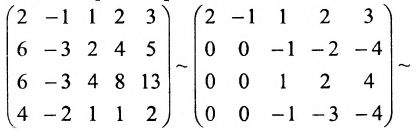
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 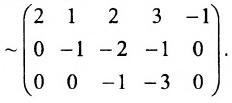
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 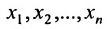
Числа 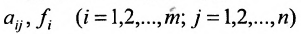
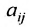
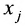
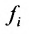
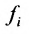
С помощью знака суммирования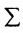
Матрица
составленная из коэффициентов системы 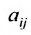
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 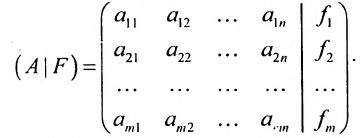
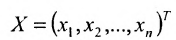
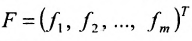

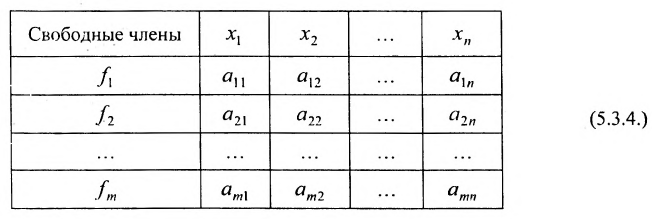
Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 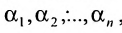
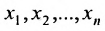
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 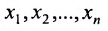
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) – значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 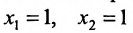
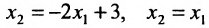
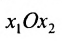
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 
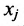
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А – матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 
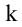
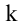
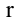
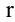
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 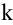
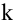
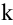
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
- Заказать решение задач по высшей математике
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 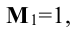
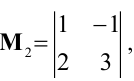
Переходим теперь к минорам 3-го порядка, окаймляющим 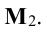
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 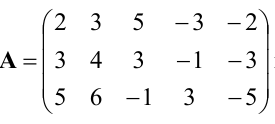
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 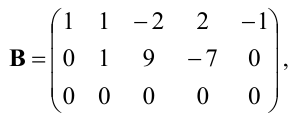
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
- Определители второго и третьего порядков и их свойства
- Метод Гаусса – определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица – определение и нахождение
-
Условия совместности.
Начать изучение
-
Нахождение решений.
Начать изучение
-
Приведенная система.
Начать изучение
-
Общее решение системы линейных уравнений.
Начать изучение
Условия совместности.
Займемся изучением систем из m уравнений с n неизвестными. Систему
begin{matrix}a_{1}^{1}x^{1}+a_{2}^{1}x^{2}+…+a_{n}^{1}x^{n}=b^{1},\a_{1}^{2}x^{1}+a_{2}^{2}x^{2}+…+a_{n}^{2}x^{n}=b^{2},\cdots\a_{1}^{m}x^{1}+a_{2}^{m}x^{2}+…+a_{n}^{m}x^{n}=b^{m}end{matrix} мы можем кратко записать в виде tag{1} Aboldsymbol{x}=boldsymbol{b}.
Система задается своей расширенной матрицей A^{*}, получаемой объединением матрицы системы A и столбца свободных членов boldsymbol{b}.
Простое и эффективное условие, необходимое и достаточное для совместности системы (1), дает следующая теорема, называемая теоремой Кронекера-Капелли.
Теорема Кронекера-Капелли.
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Иначе утверждение теоремы можно сформулировать так: приписывание к матрице A размеров m times n столбца boldsymbol{b} высоты m не меняет ее ранга тогда и только тогда, когда этот столбец — линейная комбинация столбцов A.
Доказательство.
Если mathbf{Rg},A^{*}=mathbf{Rg},A, то базисный минор A является базисным и для A^{*}. Следовательно, boldsymbol{b} раскладывается по базисным столбцам A. Мы можем считать его линейной комбинацией всех столбцов A, добавив недостающие столбцы с нулевыми коэффициентами.
Обратно, если boldsymbol{b} раскладывается по столбцам A, то элементарными преобразованиями столбцов можно превратить A^{*} в матрицу A_{0}, получаемую из A приписыванием нулевого столбца. Из утверждения о том, что ранг матрицы не меняется при элементарных преобразованиях, следует mathbf{Rg},A_{0}=mathbf{Rg},A^{*}. С другой стороны, mathbf{Rg},A_{0}=mathbf{Rg},A, так как добавление нулевого столбца не может создать новых невырожденных подматриц. Отсюда mathbf{Rg},A=mathbf{Rg},A^{*}, как и требовалось.
Утверждение 1.
Пусть матрица A^{*} приведена к упрощенному виду с помощью элементарных преобразований строк. Система (1) несовместна тогда и только тогда, когда в упрощенную матрицу входит строка begin{Vmatrix} 0&…& 0& 1 end{Vmatrix}.
Доказательство.
Пусть рассматриваемая система не совместна, и mathbf{Rg},A^{*} > mathbf{Rg},A=r. В упрощенном виде матрицы A последние m-r строк — нулевые. Последний столбец матрицы A^{*} должен быть базисным, и в упрощенном виде матрицы A^{*} последний столбец — r+1-й столбец единичной матрицы. Поэтому r+1-я строка этой матрицы есть begin{Vmatrix} 0&…& 0& 1 end{Vmatrix}. Обратно, если в матрице содержится такая строка, то последний столбец не может быть линейной комбинацией остальных, и система с упрощенной матрицей несовместна. Тогда несовместна и исходная система (согласно ранее доказанного утверждения).
Иначе это утверждение можно сформулировать так.
Следствие.
Система линейных уравнений несовместна тогда и только тогда, когда противоречивое равенство 0=1 является линейной комбинацией ее уравнений.
Равенство рангов матрицы системы и расширенной матрицы можно выразить, понимая ранг матрицы как строчный ранг. Это приведет нас к важной теореме, известной как теорема Фредгольма.
Транспонируем матрицу A системы (1) и рассмотрим систему из n линейных уравнений tag{2} begin{matrix} a_{1}^{1}y_{1}+a_{1}^{2}y_{2}+…+a_{1}^{m}y_{m}=0,\ a_{2}^{1}y_{1}+a_{2}^{2}y_{2}+…+a_{2}^{m}y_{m}=0,\cdots\a_{n}^{1}y_{1}+a_{n}^{2}y_{2}+…+a_{n}^{m}y_{m}=0end{matrix} с m неизвестными, матрицей A^{T} и свободными членами, равными нулю. Она называется сопряженной однородной системой для системы (1). Если boldsymbol{y} — столбец высоты m из неизвестных, то систему (2) можно записать как A^{T} boldsymbol{y}=boldsymbol{o}, или лучше в виде tag{3} boldsymbol{y}^{T}A=boldsymbol{o}, где boldsymbol{o} — нулевая строка длины n.
Теорема Фредгольма.
Для того чтобы система (1) была совместна, необходимо и достаточно, чтобы каждое решение сопряженной однородной системы (3) удовлетворяло уравнению tag{4} boldsymbol{y}^{T} boldsymbol{b}=y_{1}b^{1}+…+y_{m}b^{m}=0.
Доказательство.
1^{circ}. Пусть система (1) совместна, то есть существует столбец boldsymbol{x} высоты n, для которого Aboldsymbol{x}=boldsymbol{b}. Тогда для любого столбца boldsymbol{y} высоты m выполнено boldsymbol{y}^{T} Aboldsymbol{x}=boldsymbol{y}^{T} boldsymbol{b}. Если boldsymbol{y} — решение системы (3), то boldsymbol{y}^{T} boldsymbol{b}=(boldsymbol{y}^{T} A)boldsymbol{x}=boldsymbol{o}boldsymbol{x}=0.
2^{circ}. Предположим теперь, что система (1) несовместна. Тогда согласно утверждению 1 строка begin{Vmatrix} 0&…& 0& 1 end{Vmatrix} входит в упрощенный вид расширенной матрицы A^{*}=begin{Vmatrix} A& |& boldsymbol{b} end{Vmatrix} и, следовательно, является линейной комбинацией ее строк. Обозначим коэффициенты этой линейной комбинации y_{1},…, y_{m} и составим из них столбец boldsymbol{y}. Для этого столбца boldsymbol{y}^{T} begin{Vmatrix} A& |& boldsymbol{b} end{Vmatrix}=begin{Vmatrix} 0&…& 1 end{Vmatrix} (согласно данного утверждения). Это же равенство можно расписать как два: boldsymbol{y}^{T} A=boldsymbol{o} и boldsymbol{y}^{T} boldsymbol{b}=1. Итак, нам удалось найти решение системы (3), не удовлетворяющее условию (4). Это заканчивает доказательство.
В качестве примера применим теорему Фредгольма к выводу условия параллельности двух различных прямых на плоскости. Их уравнения составляют систему A_{1}x+B_{1}y+C_{1}=0, A_{2}x+B_{2}y+C_{2}=0.
Она не имеет решений, если существуют такие числа y_{1}, y_{2}, что y_{1}A_{1}+y_{2}A_{2}=0, y_{1}B_{1}+y_{2}B_{2}=0, но y_{1}C_{1}+y_{2}C_{2} neq 0. Ясно, что y_{1} и y_{2} не равны нулю. Поэтому можно положить lambda=-y_{2}/y_{1} и записать полученное условие в виде: существует число lambda такое, что A_{1}=lambda A_{2}, B_{1}=lambda B_{2} и C_{1} neq lambda C_{2}.
Нахождение решений.
В этом пункте мы будем предполагать, что дана совместная система из m линейных уравнений с n неизвестными. Ранг матрицы системы обозначим r. Поскольку ранг расширенной матрицы тоже равен r, мы можем считать базисные столбцы матрицы системы базисными столбцами расширенной матрицы. Элементарными преобразованиями строк приведем расширенную матрицу к упрощенному виду (возможность этого мы уже доказывали). Наша система линейных уравнений перейдет в эквивалентную ей систему из r линейно независимых уравнений.
Для удобства записи будем предполагать, что первые r столбцов — базисные. Тогда преобразованную систему можно записать в виде tag{5} begin{matrix} x^{1}=beta^{1}-(alpha_{r+1}^{1}x^{r+1}+…+alpha_{n}^{1}x^{n}),\cdots\x^{r}=beta^{r}-(alpha_{r+1}^{r}x^{r+1}+…+alpha_{n}^{r}x^{n}).end{matrix}
Здесь alpha_{j}^{i} и beta^{i} — элементы преобразованной расширенной матрицы. В левых частях равенств мы оставили неизвестные, соответствующие выбранным нами базисным столбцам, так называемые базисные неизвестные. Остальные неизвестные, называемые параметрическими, перенесены в правые части равенств.
Как бы мы ни задали значения параметрических неизвестных, по формулам (5) мы найдем значения базисных так, что они вместе со значениями параметрических неизвестных образуют решение системы (1). Легко видеть, что так мы получим все множество решений.
На формулах (5) можно было бы и остановиться, но ниже мы дадим более простое и наглядное, а также принципиально важное описание совокупности решений системы линейных уравнений.
Приведенная система.
Сопоставим системе линейных уравнений (1) однородную систему с той же матрицей коэффициентов: tag{6}Aboldsymbol{x}=boldsymbol{o}. По отношению к системе (1) она называется приведенной.
Утверждение 2.
Пусть boldsymbol{x}_{0} — решение системы (1). Столбец boldsymbol{x} также будет ее решением тогда и только тогда, когда найдется такое решение у приведенной системы (6), что boldsymbol{x}=boldsymbol{x}_{0}+boldsymbol{y}.
Доказательство.
Пусть boldsymbol{x} — решение системы (1). Рассмотрим разность boldsymbol{y}=boldsymbol{x}-boldsymbol{x}_{0}. Для нее Aboldsymbol{y}=Aboldsymbol{x}-Aboldsymbol{x}_{0}=boldsymbol{b}-boldsymbol{b}=boldsymbol{o}.
Обратно, если boldsymbol{y} — решение системы (6), и boldsymbol{x}=boldsymbol{x}_{0}+boldsymbol{y}, то Aboldsymbol{x}=Aboldsymbol{x}_{0}+Aboldsymbol{y}=boldsymbol{b}+boldsymbol{o}=boldsymbol{b}.
Это предложение сводит задачу описания множества решений совместной системы линейных уравнений к описанию множества решений ее приведенной системы.
Однородная система совместна. Действительно, нулевой столбец является ее решением. Это решение называется тривиальным.
Пусть столбцы матрицы A линейно независимы, то есть mathbf{Rg},A=n. Тогда система (6) имеет единственное решение (ранее мы это уже доказывали) и, следовательно, нетривиальных решений не имеет.
Утверждение 3.
Если boldsymbol{x}_{1} и boldsymbol{x}_{2} — решения однородной системы, то любая их линейная комбинация — также решение этой системы.
Доказательство.
Действительно, из Aboldsymbol{x}_{1}=boldsymbol{o} и Aboldsymbol{x}_{2}=boldsymbol{o} для любых alpha и beta следует A(alpha boldsymbol{x}_{1}+beta boldsymbol{x}_{2})=alpha A boldsymbol{x}_{1}+beta Aboldsymbol{x}_{2}=boldsymbol{o}.
Если однородная система имеет нетривиальные решения, то можно указать несколько линейно независимых решений таких, что любое решение является их линейной комбинацией. Сделаем это.
Определение.
Матрица F, состоящая из столбцов высоты n, называется фундаментальной матрицей для однородной системы с матрицей А, если:
- AF=O;
- столбцы F линейно независимы;
- ранг F максимален среди рангов матриц, удовлетворяющих условию 1).
Столбцы фундаментальной матрицы называются фундаментальной системой решений.
Если фундаментальная матрица существует, то каждый ее столбец в силу первого условия определения — решение системы. Если система не имеет нетривиальных решений, то фундаментальной матрицы нет. Это будет в том случае, когда столбцы А линейно независимы: mathbf{Rg},A=n.
Ниже мы докажем, что в остальных случаях фундаментальная матрица существует, но сначала выясним, что означает третье условие в определении.
Утверждение 4.
Пусть A — матрица размеров m times n и ранга r. Если AF=O, то mathbf{Rg},F leq n-r.
Доказательство.
Приведем матрицу A к упрощенному виду элементарными преобразованиями строк, а затем элементарными преобразованиями столбцов обратим в нулевые все небазисные столбцы. Мы получим матрицу A’=PAQ, где P и Q — произведения соответствующих элементарных матриц. Первые r строк A’ — строки единичной матрицы порядка n, а остальные — нулевые. Обозначим F’=Q^{-1}F. Тогда mathbf{Rg},F’=mathbf{Rg},F. Используя ранее доказанное нами утверждение, легко заметить, что первые r строк матрицы A’F’ совпадают с первыми r строками F’. Но A’F’=PAF=O и, следовательно, F’ содержит r нулевых строк. Так как всего в ней n строк, mathbf{Rg},F’ leq n-r. Это равносильно доказываемому утверждению.
Покажем теперь, как может быть построена фундаментальная матрица. Согласно ранее доказанному утверждению, решение однородной системы состоит из коэффициентов равной нулю линейной комбинации столбцов матрицы системы. Мы можем получить такие линейные комбинации, основываясь на теореме о базисном миноре. Снова для удобства записи будем считать, что в матрице A первые r столбцов — базисные. Каждый из небазисных столбцов boldsymbol{a}_{j} (j=r+1,…, n) раскладывается по базисным: tag{7} boldsymbol{a}_{j}=alpha_{j}^{1}boldsymbol{a}_{1}+…+alpha_{j}^{r}boldsymbol{a}_{r}. Отсюда следует, что столбец begin{Vmatrix} -alpha_{j}^{1}… -alpha_{j}^{r}& 0…0& 1& 0…0 end{Vmatrix}^{T} решением. (Единица в нем стоит на j-м месте.)
Таких решений можно составить столько, сколько есть небазисных столбцов, то есть (n-r). Убедимся в том, что эти решения линейно независимы. Для этого объединим все столбцы в одну матрицу tag{8} begin{Vmatrix} -alpha_{r+1}^{1}& -alpha_{r+2}^{1}&… -alpha_{n}^{1},\cdots\-alpha_{r+1}^{r}& -alpha_{r+2}^{r}&… -alpha_{n}^{r},\1& 0&…& 0\0& 1&…& 0\cdots\0& 0&…& 1end{Vmatrix}.
Подматрица в последних n-r строках — единичная. Поэтому ранг матрицы (8) равен числу столбцов, и столбцы линейно независимы.
Таким образом, мы получили
Утверждение 5.
Если ранг матрицы однородной системы линейных уравнений r меньше числа неизвестных n, то система имеет фундаментальную матрицу из n-r столбцов.
Итак, система столбцов (8) — фундаментальная система решений. Она называется нормальной фундаментальной системой решений. Каждому выбору базисных столбцов соответствует своя нормальная фундаментальная система решений. Вообще же, каждая система из n-r линейно независимых решений является фундаментальной.
Для нахождения матрицы (8) можно привести матрицу A системы к упрощенному виду, что даст коэффициенты разложения небазисных столбцов по базисным.
Пусть F — фундаментальная матрица системы Aboldsymbol{x}=boldsymbol{o}. Рассмотрим произвольный столбец с высоты n-r. Произведение Fboldsymbol{c} — столбец высоты n, и из равенства AFboldsymbol{c} =boldsymbol{o} следует, что при любом с столбец Fboldsymbol{c} — решение системы. Оказывается, имеет место
Утверждение 6.
Столбец boldsymbol{x} — решение системы Aboldsymbol{x}=boldsymbol{o} тогда и только тогда, когда существует такой столбец boldsymbol{c}, что tag{9} boldsymbol{x}=Fboldsymbol{c}.
Доказательство.
Остается доказать необходимость условия. Пусть boldsymbol{x} — решение. Присоединив его к F, получим матрицу F^{*}=begin{Vmatrix} F | boldsymbol{x} end{Vmatrix} . Эта матрица удовлетворяет условию AF^{*}=O, так как каждый ее столбец — решение. Значит, mathbf{Rg},F^{*}=n-r. По теореме Кронекера-Капелли мы заключаем отсюда, что существует столбец boldsymbol{c}, удовлетворяющий системе Fboldsymbol{c}=boldsymbol{x}.
Общее решение системы линейных уравнений.
Теперь мы можем собрать воедино наши результаты — утверждения 2 и 6.
Теорема 3.
Если boldsymbol{x}_{0} — некоторое решение системы (1), a F — фундаментальная матрица ее приведенной системы, то столбец tag{10} boldsymbol{x}=boldsymbol{x}_{0}+Fboldsymbol{c} при любом boldsymbol{c} является решением системы (1). Наоборот, для каждого ее решения boldsymbol{x} найдется такой столбец boldsymbol{c}, что оно будет представлено формулой (10).
Выражение, стоящее в правой части формулы (10), называется общим решением системы линейных уравнений. Если boldsymbol{f}_{1},…, boldsymbol{f}_{n-r} — фундаментальная система решений, а c_{1},…, c_{n-r} — произвольные постоянные, то формула (10) может быть написана так: tag{11} boldsymbol{x}=boldsymbol{x}_{0}+c_{1}boldsymbol{f}_{1}+…+c_{n-r}boldsymbol{f}_{n-r}.
Теорема 3 верна, в частности, и для однородных систем. Если boldsymbol{x}_{0} — тривиальное решение, то (10) совпадает с (9).
Одна из ранее доказанных нами теорем гласит, что для существования единственного решения системы из n линейных уравнений с n неизвестными достаточно, чтобы матрица системы имела детерминант, отличный от нуля. Сейчас легко получить и необходимость этого условия.
Утверждение 7.
Пусть A — матрица системы из n линейных уравнений с n неизвестными. Если det A=0, то система либо не имеет решения, либо имеет бесконечно много решений.
Доказательство.
Равенство det A=0 означает, что mathbf{Rg},A < n и, следовательно, приведенная система имеет бесконечно много решений. Если данная система совместна, то из теоремы 3 следует, что и она имеет бесконечно много решений.
Пример.
Рассмотрим уравнение плоскости как систему tag{12}Ax+By+Cz+D=0 из одного уравнения. Пусть A neq 0 и потому является базисным минором матрицы системы. Ранг расширенной матрицы 1, значит, система совместна. Одно ее решение можно найти, положив параметрические неизвестные равными нулю: y=z=0. Мы получим x=-D/A. Так как n=3, r=1, фундаментальная матрица имеет два столбца. Мы найдем их, придав параметрическим неизвестным два набора значений: y=1, z=0 и y=0, z=1. Соответствующие значения базисной неизвестной x, найденные из приведенной системы, будут -B/A и -C/A. Итак, общее решение системы (12) tag{13} begin{Vmatrix} x\ y\ z end{Vmatrix}=begin{Vmatrix} -D/A\ 0\ 0 end{Vmatrix}+c_{1} begin{Vmatrix} -B/A\ 1\ 0 end{Vmatrix}+c_{2} begin{Vmatrix} -C/A\ 0\ 1 end{Vmatrix}.
Выясним геометрический смысл полученного решения. Очевидно, прежде всего, что решение begin{Vmatrix} -D/A& 0& 0 end{Vmatrix}^{T} состоит из координат некоторой (начальной) точки плоскости, или, что то же, из компонент ее радиус-вектора. В формуле (10) решение x_0 можно выбирать произвольно. Это соответствует произволу выбора начальной точки плоскости. Мы уже знаем, что компоненты лежащих в плоскости векторов удовлетворяют уравнению Aalpha_{1}+Balpha_{2}+Calpha_{3}=0, то есть приведенной системе. Два линейно независимых решения этой системы (фундаментальная система решений) могут быть приняты за направляющие векторы плоскости. Таким образом, формула (13) — не что иное, как параметрические уравнения плоскости.
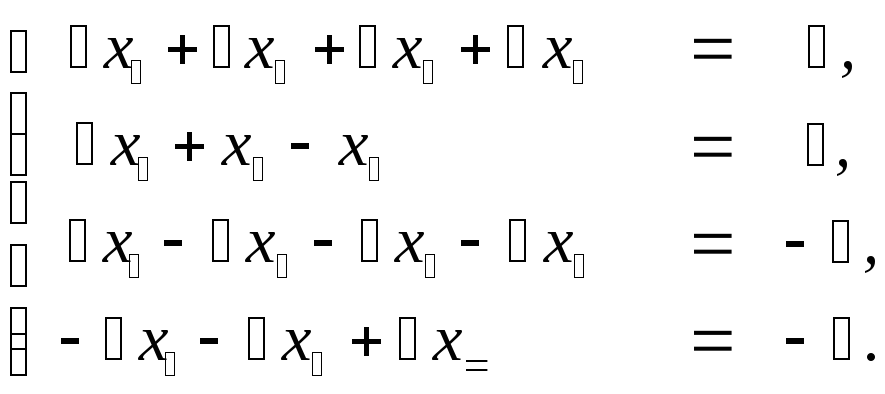
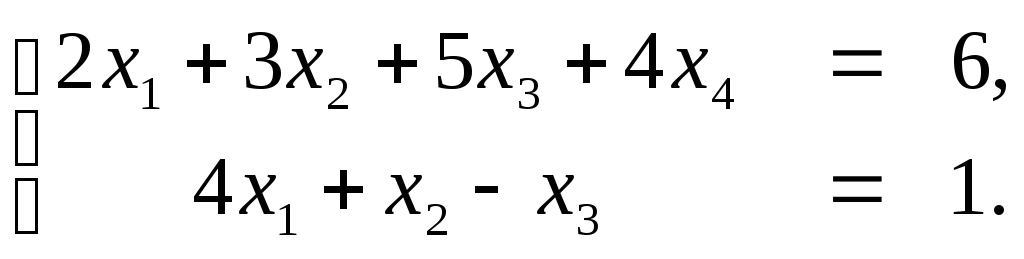
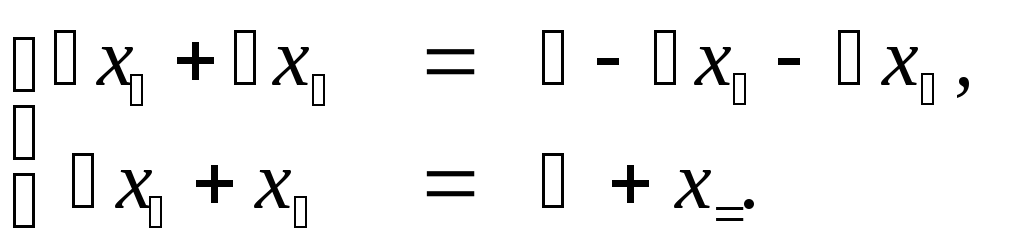
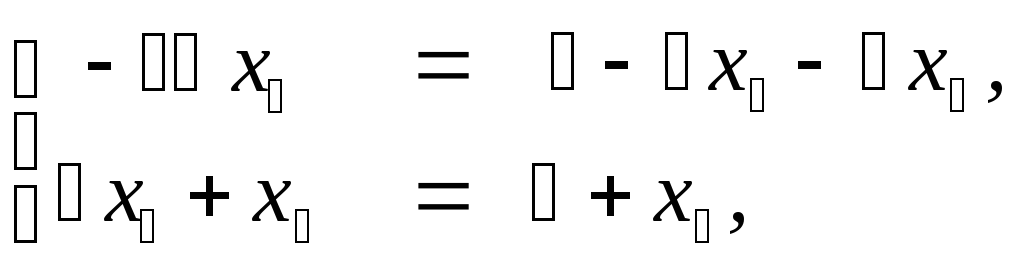
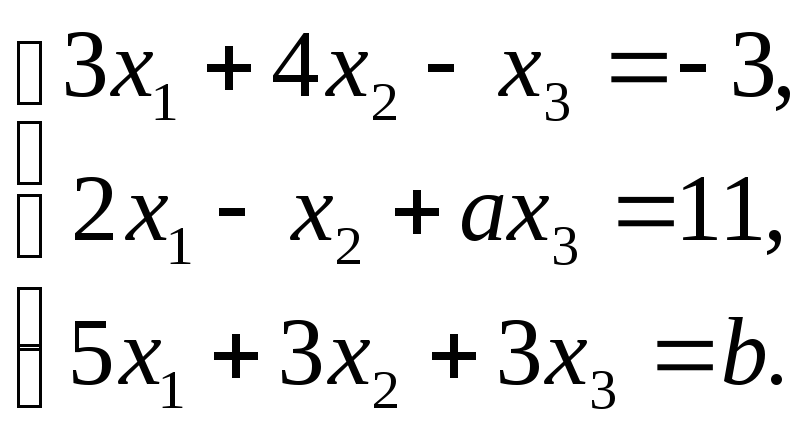
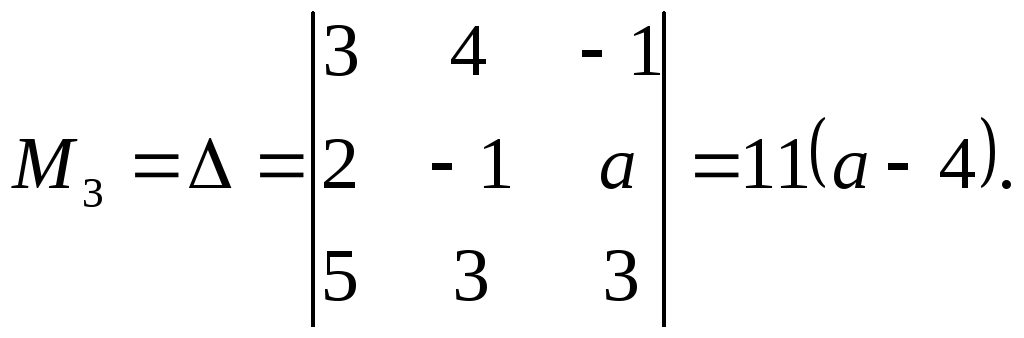



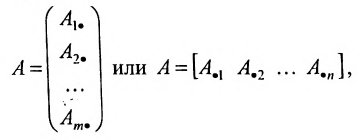
 , не равное нулю;
, не равное нулю;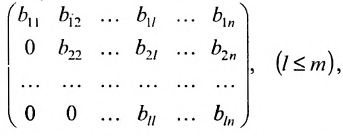
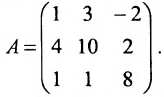
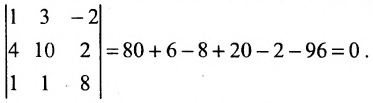



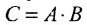 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.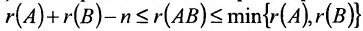 .
.