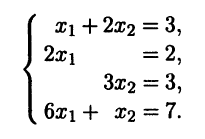Как найти ранг систем векторов

Определение
2.5. Рангом
системы векторов в
линейном
пространстве называют
размерность
линейной оболочки этой
системы
векторов.

Теорема
2.6. Ранг
системы векторов

линейного
пространства

равен:

а) максимальному
количеству линейно
независимых векторов в
системе а;

б) рангу
матрицы, составленной по столбцам из
координат
векторов

каком-либо базисе
линейного пространства
.

Пусть
g
–
некоторый базис в
.
Составим по столбцам матрицуА
из
координат в базисе g
векторов
.
Линейные операции над
векторами
соответствуют таким же линейным операциям
над столбцами их координат. Поэтому,
согласно следствию 1.1, векторы линейно
независимы тогда и только тогда, когда
столбцы их координат линейно независимы.
По теореме о базисном миноре ранг матрицыА
равен
максимальному количеству ее линейно
независимых столбцов. Это совпадает с
максимальным количеством линейно
независимых векторов в системе
.
Следовательно, утверждения а) и б) теоремы
эквивалентны.

Выберем
в матрице А
какой-либо
базисный минор и зафиксируем столбцы
этого минора (базисные столбцы).
Соответствующие им векторы будем
называть базисными. По теореме о базисном
миноре, во-первых, базисные столбцы
линейно независимы и поэтому базисные
векторы образуют линейно независимую
систему, а во-вторых, все остальные
столбцы матрицы являются линейными
комбинациями базисных и поэтому
небазисные векторы системы выражаются
через базисные. Сле­довательно, любая
линейная комбинация векторов системы
а
сводится
к линейной комбинации системы базисных
векторов, т.е. любой вектор линейной
оболочки системы векторов а
выражается
через базисные векторы. Значит, базисные
векторы образуют базис линейной оболочки.
Количество базисных векторов, с одной
стороны, равно количеству базисных
столбцов, т.е. рангу матрицы А,
а
с другой – совпадает с размерностью
линейной оболочки, т.е. с рангом системы
векторов
.

Замечание
2.2. Как
следует из приведенного доказательства,
столбцы любого базисного минора матрицы
А
отвечают
набору векторов системы

являющемуся
базисом в
линейном подпространстве, порожденном
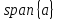
этой системой векторов.

Пример
2.11. Пусть
даны векторы

в
четырехмерном линейном пространстве
,
имеющие в некотором базисе столбцы
координат,,.
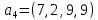
Соответствующая матрицаА
имеет
вид

Вычислив
ранг матрицы, убеждаемся, что он равен
2. Таким образом, ранг системы векторов
равен 2. Легко проверить, что любой минор
второго порядка является базисным.
Поэтому базисом линейной оболочки этой
системы векторов будут

Вопросы и задачи

1. Может
   ли линейное подпространство состоять
   из: а) двух элементов; б) одного элемента;
   г)
   100 элементов?

2. Может
   ли линейное подпространство конечномерного
   линейного пространства быть
   бесконечномерным?

3. Докажите,
   что бесконечномерное линейное
   пространство содержит собственные
   бесконечномерные линейные подпространства.

4. По
   аналогии с суммой двух линейных
   подпространств определите сумму
   конечного числа линейных подпространств.

1. Найдите
   максимальное число линейно независимых
   векторов в системе векторов, заданных
   своими координатами

в
некотором базисе линейного пространства
размерности 4.

2.7. Докажите,
что линейным подпространством является
множество всех векторов п-мерного
линейного арифметического пространства,
удовлетворяющих условию:

а) первые
две координаты равны между собой;

б) первая
координата равна нулю;

в) координаты
удовлетворяют уравнению
.

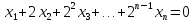
Найдите
базис и размерность этого линейного
подпространства.

2.8. Найдите
размерность и базис линейной оболочки
следующих векторов из
:

.

Соседние файлы в папке re

• #
• #
• #
• #
• #
• #
• #
• #
• #

Как найти ранг векторов

Алгоритм нахождения базиса системы векторов

Для того чтобы найти базис системы векторов A_v А₂. А , необходимо:

1) составить соответствующую системе векторов однородную систему уравнений

2) привести эту систему к равносильной разрешенной системе вида

• 3) записать базис системы векторов Б = (А_рА₂, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
• 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора

в разрешенной системе уравнений, т.е.

Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.

Пример 3.3. Найти ранг и базис системы векторов

разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.

Решение. Составим систему уравнений A _t ay + А₂х₂ + . + А„х_п = 0, которая в координатной записи имеет вид

Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.

Разрешенная система имеет вид

В базис системы векторов включаем 1-й и 2-й векторы Б_: = (A_VA₂), которые соответствуют разрешенным неизвестным х₁ и х₂. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.

Запишем разложения векторов по базису. Коэффициентами разложения вектора А₃ являются координаты вектора А’₃ = (3, -2), т.е. коэффициенты при х₃ в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х₃ А₃ = ЗЛ₁ — 2А_г Аналогично, коэффициентами разложения вектора А₄ являются координаты вектора А’₄ = (4, 1) А₄ = 4А_у + 1 А_т

Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я₉₄ = 1.

86. Ранг системы векторов и ранг матрицы. Основная теорема о двух системах векторов

Теорема 1. Пусть даны две системы векторов A1, A2, . AK, и B1, B2, . BM, которые обладают свойствами:

1) первая система линейно независима;

2) каждый вектор первой системы линейная комбинация векторов второй системы.

Тогда k £ m, т. е. число векторов первой системы не больше числа векторов второй системы.

Доказательство. Доказательство проводим методом математической индукции по числу векторов второй системы, т. е. по M.

Пусть M=1. Докажем, что K=1. Допустим противное, что K>1. Тогда по второму условию каждый вектор системы A1, A2, . AK линейно выражается через вектор B1, т. е. AI = aIBI ; I=1,2. K, где все числа aI ≠ 0 ; I=1,2. K. Действительно, в противно случае какой-нибудь вектор AI = 0 и по свойству система A1, A2, . AK линейно зависим, что противоречит условию. Тогда из первых двух равенств первой системы получаем, что

Отсюда вектора A1, A2 образуют линейно зависимую подсистему системы векторов A1, A2, . AK, что противоречит свойству. Установленное противоречие доказывает справедливость теоремы при M=1.

Предположим, что утверждение теоремы справедливо для любой системы второго вида, содержащей M — 1 вектор, и докажем его для системы содержащей M векторов. По второму условию имеем систему K равенств :

Онлайн калькулятор. Ранг матрицы.

Используя этот онлайн калькулятор для вычисления ранга матрицы, вы сможете очень просто и быстро найти ранг матрицы.

Воспользовавшись онлайн калькулятором для вычисления ранга матрицы, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисления ранга матрицы, а также закрепить пройденный материал.

Найти ранг матрицы

Введите значения Матрицы:

Ввод данных в калькулятор ранга матриц

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора ранга матриц

• Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.

Теория. Ранг матриц.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Базис и ранг системы векторов

Часть системы векторов называется базисом этой системы, если:

• 1) часть является линейно независимой системой векторов;
• 2) каждый вектор системы разлагается по векторам части.

Диагональная система векторов является базисом каждой системы, которая содержит ее в качестве части.

Если система уравнений

является разрешенной, то векторы-коэффициенты при неизвестных, составляющих набор разрешенных неизвестных, образуют диагональную часть системы векторов А_г, А₂, . А_п.

Векторы системы разлагаются по базису этой системы единственным образом.

Каждую линейно независимую часть системы векторов можно дополнить до базиса этой системы.

Все базисы данной системы векторов состоят из одного и того же числа векторов.

Рангом системы векторов называется число векторов в любом ее базисе. Если ранг системы векторов равен г, то каждая линейно независимая часть этой системы, состоящая из г векторов, является ее базисом. Системы векторов называются эквивалентными, если векторы одной системы разлагаются по векторам другой системы и наоборот. Ранги эквивалентных систем равны.

Построение базиса системы векторов А^, А₂, . А_п и разложений векторов по базису:

1. Рассмотреть систему уравнений А₁х₁+ А₂х₂ + . + А_пх_п = 0 и найти равносильную ей разрешенную систему уравнений

• 2. Найти диагональную часть системы векторов А, А’₂ , . А’_п.
• 3. Отметить векторы системы Ар А₂, . А_п, соответствующие диагональной части системы А, А’₂ , . А_п; они образуют базис системы -^•1,-^2» •••>
• 4. Разложить вектор Aj по диагональной части системы А’_г , А’₂ , . А_п ; вектор А,, 1

Разрешенная система уравнений, равносильная исходной, имеет вид

0 ’ А 4 = 1 ’ А 5 = 1

Разложим теперь векторы А₂ и А₃ по базису А_1г А₃, А₄. Для этого сначала разложим соответствующие векторы А₂ и А’₅ по диагональной системе А’₄ , А’₃ , А₄ , имея в виду, что коэффициентами разложения вектора по диагональной системе являются его координаты:

Векторы А₂ и А₅ разлагаются по базису Ар А₃, А₄ с теми же коэффициентами, что и векторы А’₂ и А₃ по диагональной системе А₄ , А’₃ , А₄ :

Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:

4.47. Найти базис системы векторов

содержащий вектор А₅, и все векторы, не входящие в этот базис, разложить по базису.

4.48. Найти базис системы векторов

содержащий векторы А₂ и А₃, и векторы, не входящие в этот базис, разложить по базису.

4.49. Найти два базиса системы векторов

единственными общими векторами которых служат А₂ и А₄.

Найти все базисы системы векторов:

4.53. Ai = (1, 0, 1, 0),

• 4.54. Доказать, что линейно зависимая система ненулевых векторов содержит два различных базиса.
• 4.55. Доказать, что система векторов, имеющая только один базис, линейно независима.
• 4.56. Вектор разлагается по остальным векторам системы A_lf А₂, . А_т, которая не содержит нулевых векторов. Доказать, что система A_lt А₂, . » А_т обладает базисом, который не содержит вектора Ар
• 4.57. Вектор А_г не разлагается по остальным векторам системы Ар А₂, . А_т, которая не содержит нулевых векторов. Доказать, что каждый базис системы векторов A_lf А₂, . А_тсодержит вектор Ар
• 4.58. Каждый вектор системы Ар А₂, . А_т разлагается по своей части В₁₉ В₂, . В_k. Доказать, что каждый базис системы векторов Вр В₂, является базисом системы Ар А₂, . А_т.
• 4.59. Найти какой-нибудь базис системы ненулевых векторов Ар А₂, А₃, А₄, если каждый вектор этой системы разлагается по предыдущим векторам.
• 4.60. Доказать, что если в системе Ар А₂, . А_т, А₁ Ф 0, вычеркнуть все векторы, которые разлагаются по предыдущим векторам, то получится базис системы Ар А₂, . А_т.
• 4.61. Каждая линейная комбинация векторов Вр В₂, . В_т, отличная от нулевого вектора, не разлагается по системе векторов Ар А₂, . »А_п. Доказать, что объединение базисов систем векторов Ар А₂, . А_п и Вр В₂, . В_т будет базисом объединенной системы Ар А₂, . А_п, Вр В₂, . В_т.
• 4.62. Найти все различные базисы системы ненулевых векторов Ар А₂, А₃, А₄, если каждый вектор этой системы разлагается по предыдущим векторам.
• 4.63. В системе векторов Ар А₂, А₃, А₄, А₅ ранга 3 векторы А₁ и А₃, а также А₂ и А₄ пропорциональны. Найти все базисы этой системы.

• 4.64. В системе А_1? А₂, А₃, А₄ ранга 3 вектор А₄ = 2А₁ – А₃. Найти все базисы этой системы векторов.
• 4.65. Система ненулевых векторов А₁,А₂, . A_k+1, содержащая два пропорциональных вектора, имеет ранг k. Сколько различных базисов содержит эта система?
• 4.66. Система векторов А_х – А₂, А₂ – А₃, А₃ – А₄, А₄ + Aj линейно независима и вектор В не разлагается по этой системе. Найти ранг системы векторов Ар А₂, А₃, А₄, В.
• 4.67. Доказать, что ранг системы А_г + В_±, А₂ + В₂, . А_п + В_п не превосходит ранга системы векторов Ар А₂, . А_п, Вр в₂. в_п.
• 4.68. Ранг системы векторов Ар А₂, . А_п равен г. Найти ранг системы векторов Ар А₂ – Ар . А_п – А_п _ j.
• 4.69. Пусть ранг системы векторов Ар А₂, . А_т равен k. Доказать, что каждая часть системы векторов Ар А₂, . А_т, содержащая более k векторов, линейно зависима.
• 4.70. Ранг некоторой части системы векторов равен рангу всей системы векторов. Доказать, что каждый базис этой части является базисом всей системы векторов.
• 4.71. Доказать, что ранг системы векторов Ар А₂, . Ар A_{fe +} p . А_т не превосходит суммы рангов ее частей Ар А₂, . А_йиА_й+р . А _то.
• 4.72. Пусть ранг системы векторов Ар А₂, . А_т равен г и вектор В не разлагается по системе Ар А₂, . А_т. Доказать, что ранг системы векторов Ар А₂, . А_т, В равен г -I- 1.
• 4.73. Каждый вектор системы A_lf А₂, . А_т ранга г разлагается по векторам системы ВрВ₂,В_п ранга r+ 1. Доказать, что в системе Вр В₂, . В_п найдется такой вектор, который не разлагается по системе Ар А₂, . А_т.
• 4.74. Векторы Вр В₂, . В_г образуют базис системы A_lfА₂, . А_т hAj — ненулевой вектор, не входящий в этот базис. Доказать, что в системе Вр В₂, . В_г найдется такой вектор B_z,

87. Базис и ранг системы векторов. Теорема о базисах

Пусть V векторное пространство над полем Р, S – система векторов из V.

Определение 1. Базисом системы векторов S называется такая упорядоченная линейно независимая подсистема B1, B2, . BR системы S, что любой вектор системы S линейная комбинация векторов B1, B2, . BR.

Определение 2. Рангом системы векторов S называется число векторов базиса системы S. Обозначается ранг системы векторов S символом R = rangS.

Если S = <0>, то система не имеет базиса и предполагается, что rangS = 0.

Пример 1. Пусть дана система векторов A1 = (1,2), A2 = (2,3), A3 = (3,5), A4 = (1,3). Вектора A1 , A2 образуют базис данной системы, так как они линейно независимы (см. пример 3.1) и A3 = A1 + A2 , A4 = 3A1 – A2 . Ранг данной системы векторов равен двум.

Теорема 1 (теорема о базисах). Пусть S – конечная система векторов из V , S ≠<0>. Тогда справедливы утверждения.

1° Любую линейно независимую подсистему системы S можно дополнить до базиса.

2° Система S обладает базисом.

2° Любые два базиса системы S содержат одинаковое число векторов, т. е. ранг системы не зависит от выбора базиса.

4° Если R = rangS, то любые r линейно независимых векторов образуют базис системы S.

5° Если R = rangS, То любые k > r векторов системы S линейно зависимы.

6° Любой вектор A € S единственным образом линейно выражается через вектора базиса, т. е., если B1, B2, . BR базис системы S, то

И такое представление единственно.

В силу 5° базис это Максимально линейно независимая подсистема системы S, а ранг системы S число векторов в такой подсистеме.

Представление вектора A в виде (1) называется Разложением вектора по векторам базиса, а числа a1, a2, . ar называются Координатами вектора A В данном базисе.

Доказательство. 1° Пусть B1, B2, . BK – линейно независимая подсистема системы S. Если каждый вектор системы S Линейно выражается через вектора нашей подсистемы, то по определению она является базисом системы S.

Если имеется вектор в системе S , который линейно не выражается через вектора B1, B2, . BK , то обозначим его через BK+1 . Тогда системы B1, B2, . BK , BK+1 – линейно независима. Если каждый вектор системы S Линейно выражается через вектора этой подсистемы, то по определению она является базисом системы S.

Если имеется вектор в системе S , который линейно не выражается через B1, B2, . BK , BK+1, то повторим рассуждения. Продолжая этот процесс, мы либо придем к базису системы S , либо увеличим число векторов в линейно независимой системе на единицу. Так как в системе S конечное число векторов, то вторая альтернатива не может продолжаться бесконечно и на некотором шаге получим базис системы S.

2° Пусть S конечная система векторов и S ≠<0>. Тогда в системе S есть вектор B1 ≠ 0, который образует линейно независимую подсистему системы S . По первой части его можно дополнить до базиса системы S . Таким образом система S обладает базисом.

3° Допустим, что система S имеет два базиса:

По определению базиса система векторов (2) линейно независима и (2) Í S . Далее по определению базиса каждый вектор системы (2) линейная комбинация векторов системы (3). Тогда по основной теореме о двух системах векторов R £ S. Аналогично доказавается, что S £ R. Из этих двух неравенств следует R = S.

4° Пусть R = rangS, A1, A2, . AR – линейно независимая подсистема S. Покажем, что она является базисом систем S. Если она не является базисом, то по первой части ее можно дополнить до базиса и получим базис A1, A2, . AR, AR+1. AR+T , содержащий более чем R векторов. Это противоречит доказанному в третьей части.

5° Если K векторов A1, A2, . AK (K > R) системы S – линейно независимы, то по первой части эту систему векторов можно дополнить до базиса и получим базис A1, A2, . AK, AK+1. AK+T , содержащий более чем R векторов. Это противоречит доказанному в третьей части.

6° Пусть B1, B2, . BR базис системы S. По определению базиса любой вектор A € S есть линейная комбинация векторов базиса:

Доказывая единственность такого представления допустим противное, что есть еще одно представление:

Вычитая равенства почленно находим

Так как базис B1, B2, . BR линейно независимая система, то все коэффициенты ai – bi =0; I = 1, 2, . R. Следовательно, ai = bi ; I = 1, 2, . R и единственность доказана.

[spoiler title=”источники:”]

http://vuzdoc.ru/196041/ekonomika/bazis_rang_sistemy_vektorov

http://matica.org.ua/metodichki-i-knigi-po-matematike/algebra-i-geometriia-tolstikov-a-v/87-bazis-i-rang-sistemy-vektorov-teorema-o-bazisakh

[/spoiler]

Определение 2.5. Рангом системы векторов в линейном пространстве называют размерность линейной оболочки этой системы векторов.

Теорема 2.6. Ранг системы векторов а = (a₁ … а_k) линейного пространства L равен:

а) максимальному количеству линейно независимых векторов в системе а;

б) рангу матрицы, составленной по столбцам из координат векторов a₁,…, a_k в каком-либо базисе линейного пространства L.

◄ Пусть g – некоторый базис в L. Составим по столбцам матрицу А из координат в базисе g векторов а_i, i = 1,k. Линейные операции над векторами а_i соответствуют таким же линейным операциям над столбцами их координат. Поэтому, согласно следствию 1.1, векторы линейно независимы тогда и только тогда, когда столбцы их координат линейно независимы. По теореме о базисном миноре [III] ранг матрицы А равен максимальному количеству ее линейно независимых столбцов. Это совпадает с максимальным количеством линейно независимых векторов в системе о. Следовательно, утверждения а) и б) теоремы эквивалентны.

Выберем в матрице А какой-либо базисный минор и зафиксируем столбцы этого минора (базисные столбцы). Соответствующие им векторы будем называть базисными. По теоремр о базисном миноре, во-первых, базисные столбцы линейно неза-висимы и поэтому базисные векторы образуют линейно незави: симую систему, а во-вторых, все остальные столбцы матрицы являются линейными комбинациями базисных и поэтому неба-зисные векторы системы выражаются через базисные. Сле-довательно, любая линейная комбинация векторов системы а сводится к линейной комбинации системы базисных векторов, т.е. любой вектор линейной оболочки системы векторов а вы-ражается через базисные векторы. Значит, базисные векторы образуют базис линейной оболочки. Количество базисных век-торов, с одной стороны, равно количеству базисных столбцов, т.е. рангу матрицы А, а с другой – совпадает с размерностью линейной оболочки, т.е. с рангом системы векторов а. ►

Замечание 2.2. Как следует из приведенного доказательства, столбцы любого базисного минора матрицы А отвечают набору векторов системы a, являющемуся базисом в span{a} – линейном подпространстве, порожденном этой системой векторов.

Пример 2.11. Пусть даны векторы a₁, a₂, а₃, а₄ в четырехмерном линейном пространстве L, имеющие в некотором базисе столбцы координат a₁ = (1 2 0 6)^T , а₂ = (2 0 3 1)^T ,а₃ = (3 2 3 7)^T , a₄ = (7 2 9 9)^T . Соответствующая матрица А имеет вид

Вычислив ранг матрицы, убеждаемся, что он равен 2. Таким образом, ранг системы векторов равен 2. Легко проверить, что любой минор второго порядка является базисным. Поэтому базисом линейной оболочки этой системы векторов будут любые два вектора системы. Например, базисом является пара векторов a₁, a₂. По этому базису можно разложить, напримep, остальные векторы системы. Чтобы найти разложение вектора а₃ по базису, достаточно решить систему линейных алгебраических уравнений

х₁а₁ + x₂a₂ = а₃

которая в координатной форме имеет вид

Из четырех уравнений можно оставить любые два. Используя второе и третье уравнения, находим x₁ = 1, x₂ = 1 и, следовательно, а₃ = a₁ + a₂. Аналогично находим и разложение вектора a₄: a₄ = a₁ + 3a₂.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ